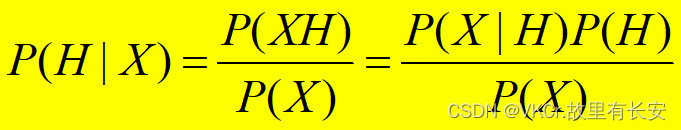K-近邻算法(KNN)
K-近邻分类法的基本思想:通过计算每个训练数据到待分类元组Zu的距离,取和待分类元组距离最近的K个训练数据,K个数据中哪个类别的训练数据占多数,则待分类元组Zu就属于哪个类别。
KNN算法描述:
- 对新的数据集中的每一个数据点,计算其到已知分类信息的数据集中所有数据点的距离。
- 将计算得到的所有距离进行排序,一般是升序排序。
- 选取其中前K个与未知点离得最近的点。
- 统计这K个已知分类信息中各个类别出现的频数,
- 选取上述K个点中类别频数最高的,作为未知点的类别。
eg:设某公司现有8名员工的基本信息,包括其个子为高个,中等,矮个的分类标识
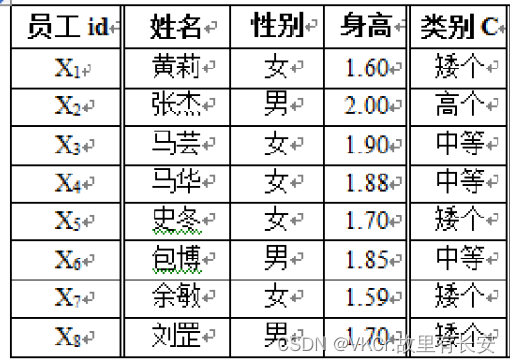
公司现刚招进一位名叫刘萍的新员工Z1,令k=5,试采用 k-NN分类算法判断员工刘萍的个子属于哪一类?
解:

决策树
决策树是通过一系列规则对数据进行分类的过程。它提供一种在什么条件下会得到什么值的类似规则的方法。通常决策树主要有三种实现,分别是ID3算法,CART算法和C4.5算法
决策树分为分类树和回归树两种,分类树对离散变量做决策树,回归树对连续变量做决策树。
决策树分类方法采用自顶向下的递归方式
一棵决策树的生成过程主要分为以下3个部分:
- 特征选择
- 决策树生成
- 剪枝
研究结果表明,一般情况下, 树越小则树的预测能力越强。
理论上讲,后剪枝好于预先剪枝,但计算复杂度大。
典型决策树算法
ID3
ID3算法用信息增益作为属性测试条件,且信息增益值越大以该属性作为分支结点越好。
ID3算法的核心在于使用"信息熵"作为衡量标准,通过计算每个属性的信息增益,选择信息增益最高的属性作为划分标准,重复这个过程直至生成一个能完美分类训练的决策树,采用贪心算法,不能保证全局最优.
递归终止条件:①当分到某个类时,目标属性全是一个值. OR ②当分到某个类时,某个值的比例达到给定的阈值.
信息熵E,一个系统越是有序,信息熵越低;反之,一个系统越混乱,信息熵越高.
info信息量
若存在n个相同概率的消息,则每个消息的概率p=1/n,一个消息传递的信息量为: -Log2(1/n)=Log2n (使用以2为底的对数函数,是因为计算机中的信息用二进位编码。)
gain信息增益 ,选择gain(max)作为结点
|----|----|----|----|---|-----|
| 序号 | 天气 | 气温 | 湿度 | 风 | 打网球 |
| 1 | 晴 | 热 | 高 | 无 | N |
| 2 | 晴 | 热 | 高 | 有 | N |
| 3 | 多云 | 热 | 高 | 无 | Y |
| 4 | 雨 | 温暖 | 高 | 无 | Y |
| 5 | 雨 | 凉爽 | 正常 | 无 | Y |
| 6 | 雨 | 凉爽 | 正常 | 有 | N |
| 7 | 多云 | 凉爽 | 正常 | 有 | Y |
| 8 | 晴 | 温暖 | 高 | 无 | N |
| 9 | 晴 | 凉爽 | 正常 | 无 | Y |
| 10 | 雨 | 温暖 | 正常 | 无 | Y |
| 11 | 晴 | 温暖 | 正常 | 有 | Y |
| 12 | 多云 | 温暖 | 高 | 有 | Y |
| 13 | 多云 | 热 | 正常 | 无 | Y |
| 14 | 雨 | 温暖 | 高 | 有 | N |



ID3优点:算法的理论清晰,方法简单,学习能力较强。
决策树ID3算法的主要问题:过拟合,对数据中的噪声敏感以及不稳定.只能处理离散属性数据,不能处理有缺失的数据。
改进策略:使用决策树的改进版本,如随机森林何梯度提升.
C4.5
C4.5和ID3都是利用贪心算法进行求解,不同的是分类决策的依据不同.
C4.5算法在结构和递归上与ID3完全相同,区别在于选取决断特征时选择信息增益比最大的.
C4.5既可以处理离散型属性,也可以处理连续型属性.
CART
CART算法构成的是一个二叉树,它在每一步的决策时只能是"是"或者"否",即使一个feature有多个取值,也是把数据分为两部分。选择Gini系数最小值作为结点
|----|-----|----|------|------|
| ID | 有房者 | 婚姻 | 年收入 | 拖欠贷款 |
| 1 | 是 | 单身 | 125K | 否 |
| 2 | 否 | 已婚 | 100K | 否 |
| 3 | 否 | 单身 | 70K | 否 |
| 4 | 是 | 已婚 | 120K | 否 |
| 5 | 否 | 离异 | 95K | 是 |
| 6 | 否 | 已婚 | 60K | 否 |
| 7 | 是 | 离异 | 220K | 否 |
| 8 | 否 | 单身 | 85K | 是 |
| 9 | 否 | 已婚 | 75K | 否 |
| 10 | 否 | 单身 | 90K | 是 |
解: 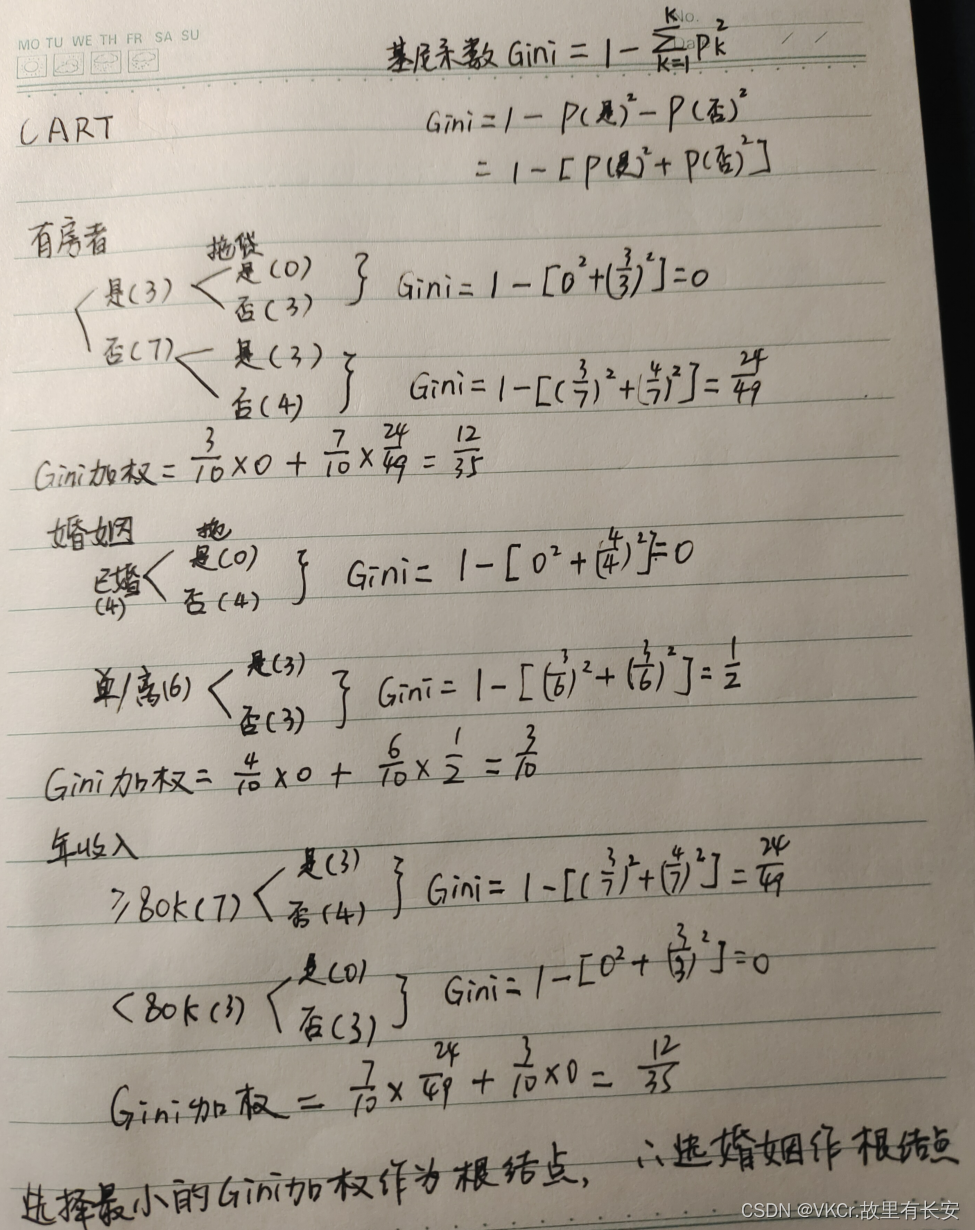

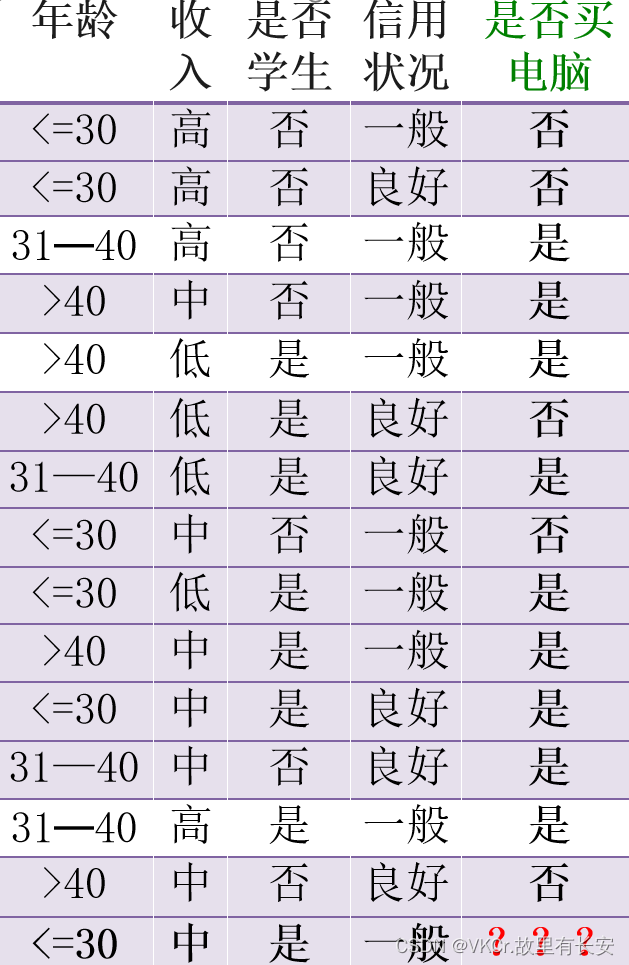
朴素贝叶斯
整个朴素贝叶斯分类可分为三个阶段:
第一阶段是准备工作阶段
第二阶段是分类器训练阶段
第三阶段是应用阶段