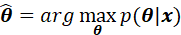题目
考虑矢量MAP估计量
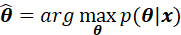
证明这个估计量对于代价函数
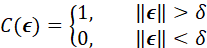
使贝叶斯风险最小。其中: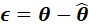 ,
, 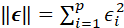 , 且
, 且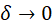 .
.
解答
贝叶斯风险函数:
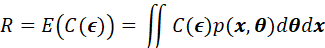
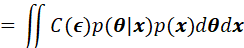
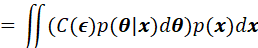
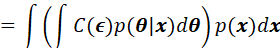
基于概率密度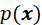 的非负特性,上述对
的非负特性,上述对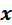 积分要求最小,那就需要内层积分达到最小。令内层积分为:
积分要求最小,那就需要内层积分达到最小。令内层积分为:
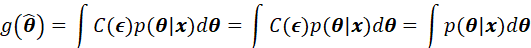
上述积分的区域为: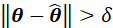 ,根据概率密度函数积分的形式,上式也等于:
,根据概率密度函数积分的形式,上式也等于:
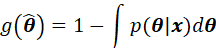
此时,上式函数的积分区域转化为: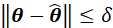
当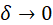 时,仍然要保证
时,仍然要保证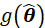 最小,那么就需要在
最小,那么就需要在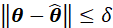 区域上,确保积分
区域上,确保积分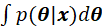 最大,那么只有寻找到
最大,那么只有寻找到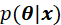 函数的最大值,并令最大值就是
函数的最大值,并令最大值就是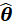 才能满足要求,即:
才能满足要求,即:
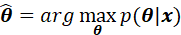
考虑矢量MAP估计量
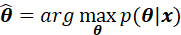
证明这个估计量对于代价函数
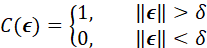
使贝叶斯风险最小。其中: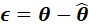 ,
, 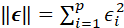 , 且
, 且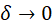 .
.
贝叶斯风险函数:
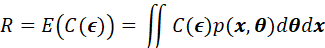
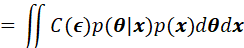
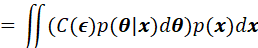
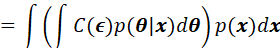
基于概率密度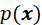 的非负特性,上述对
的非负特性,上述对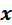 积分要求最小,那就需要内层积分达到最小。令内层积分为:
积分要求最小,那就需要内层积分达到最小。令内层积分为:
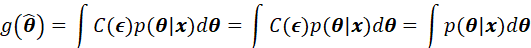
上述积分的区域为: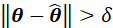 ,根据概率密度函数积分的形式,上式也等于:
,根据概率密度函数积分的形式,上式也等于:
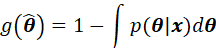
此时,上式函数的积分区域转化为: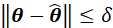
当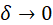 时,仍然要保证
时,仍然要保证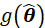 最小,那么就需要在
最小,那么就需要在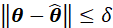 区域上,确保积分
区域上,确保积分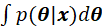 最大,那么只有寻找到
最大,那么只有寻找到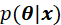 函数的最大值,并令最大值就是
函数的最大值,并令最大值就是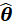 才能满足要求,即:
才能满足要求,即: