汽车雷达高级信号处理和建模技术简介------文章精读(上)
Biswas P, Sur S N, Bera R, et al. Advanced Signal Processing and Modeling Techniques for Automotive Radar: Challenges and Innovations in ADAS Applications[J]. Computer Modeling in Engineering & Sciences (CMES), 2025, 144(1).
1. 前言
文章从 ADAS/自动驾驶的传感器融合开始谈起,强调雷达在雨雾夜晚等条件下的稳健性、对距离/速度的直接可测性以及相对较低的计算与成本开销。随后把车载雷达"落地部署"的主要瓶颈归为现实道路的多径、强杂波与雷达密集带来的互扰,这些因素使得传统"做个 FFT 再阈值"的方法不够用,必须引入更系统的信号建模与更强的阵列/统计方法。其整体逻辑主线可以概括成一条连续的流水线:先在波形与调制 层面确保距离与速度可分、分辨率可控,再在互扰模型 层面把"别人的雷达"转成可计算的 INR/PSD,再在检测 层面把高维数据(距离/多普勒/方位/俯仰)做谱域分离并用 CFAR 控制虚警,进而在DOA(到达角)层面用波束形成或子空间法实现多目标角分辨,最后把检测点交给跟踪模块形成稳定航迹,为 ACC/AEB/LCA 等功能提供可用对象。
2. 系统形态与应用驱动的硬件布置(Fig. 1--3)
Fig. 1:360° 环视雷达覆盖与 ADAS 功能对应关系
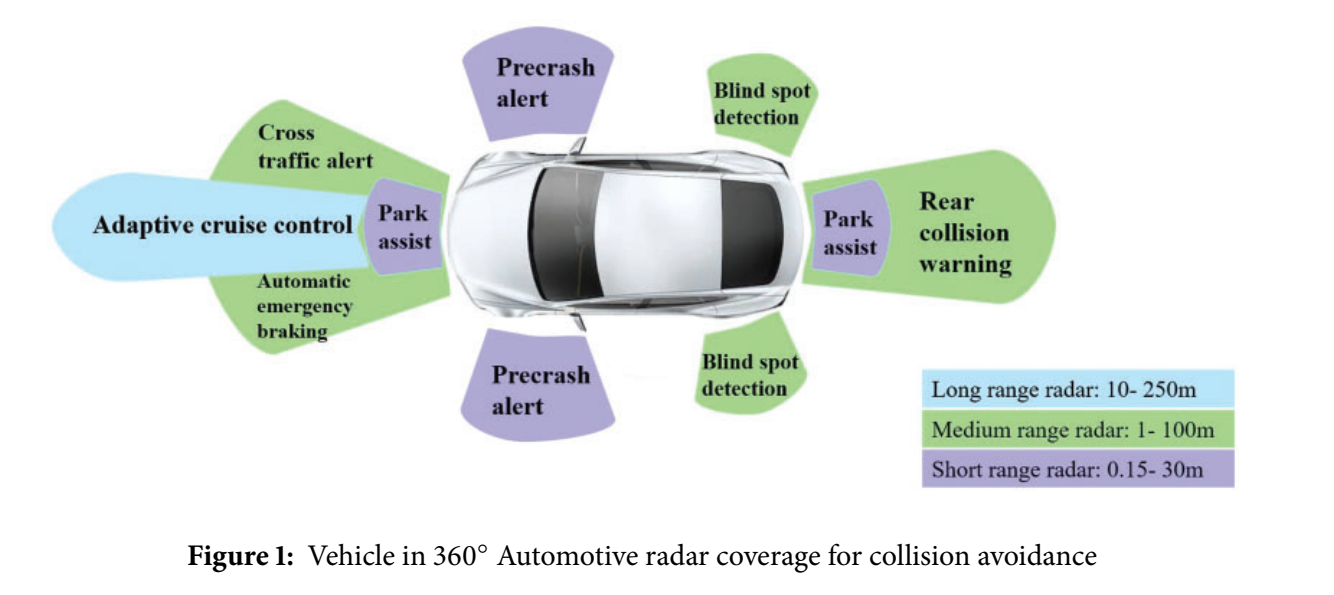
前向区域对应 Adaptive cruise control(自适应巡航)、Automatic emergency braking(自动紧急制动),侧向/后向区域对应 Cross traffic alert(横向来车预警)、Blind spot detection(盲区检测)、Rear collision warning(后向碰撞预警),近距区域标注 Park assist(泊车辅助)。右下角用彩色条给出三类雷达量程:LRR(约 10--250 m)、MRR(约 1--100 m)、SRR(约 0.15--30 m)。事实上,车载雷达不是"一个雷达做所有事",而是按视场/量程/分辨率需求做系统级布置;这会直接决定波形参数、阵列孔径与信号处理预算。
Fig. 2:汽车雷达处理系统的高层框图
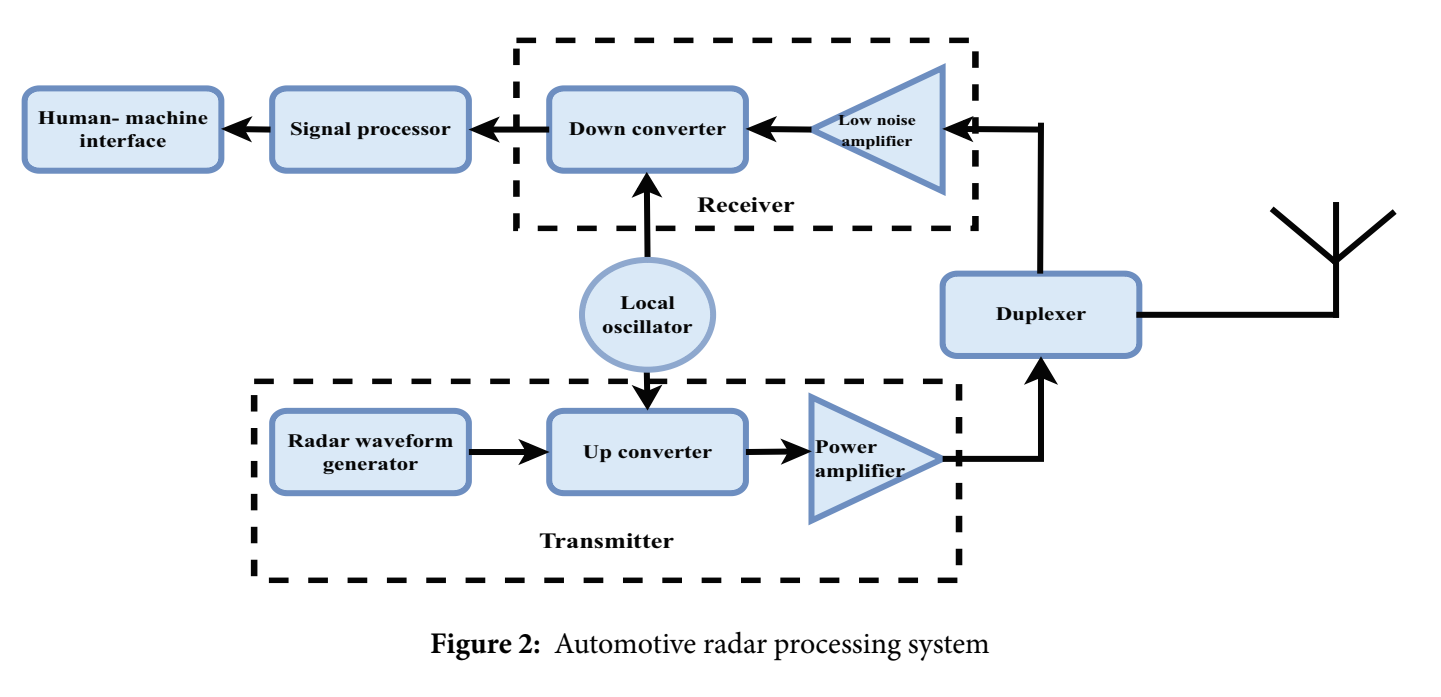
"Transmitter---Duplexer---Receiver---Signal processor---Human-machine interface"串起整机:发射端包含 waveform generator(波形发生器)、up converter(上变频)、power amplifier(功放);接收端包含 low-noise amplifier(低噪放)与 down converter(下变频);local oscillator(本振)同时给上下变频;duplexer(双工器)连接天线,实现收发共用或隔离。文章在正文紧接着指出:接收回波与发射信号副本混频后得到 beat frequency,随后通过快时间 FFT 得距离、慢时间 FFT 得速度,再用 beamforming/DOA 算法得角度。
Fig. 3(PDF 第 5 页):随自动驾驶等级演进的雷达数量/频段/成本趋势
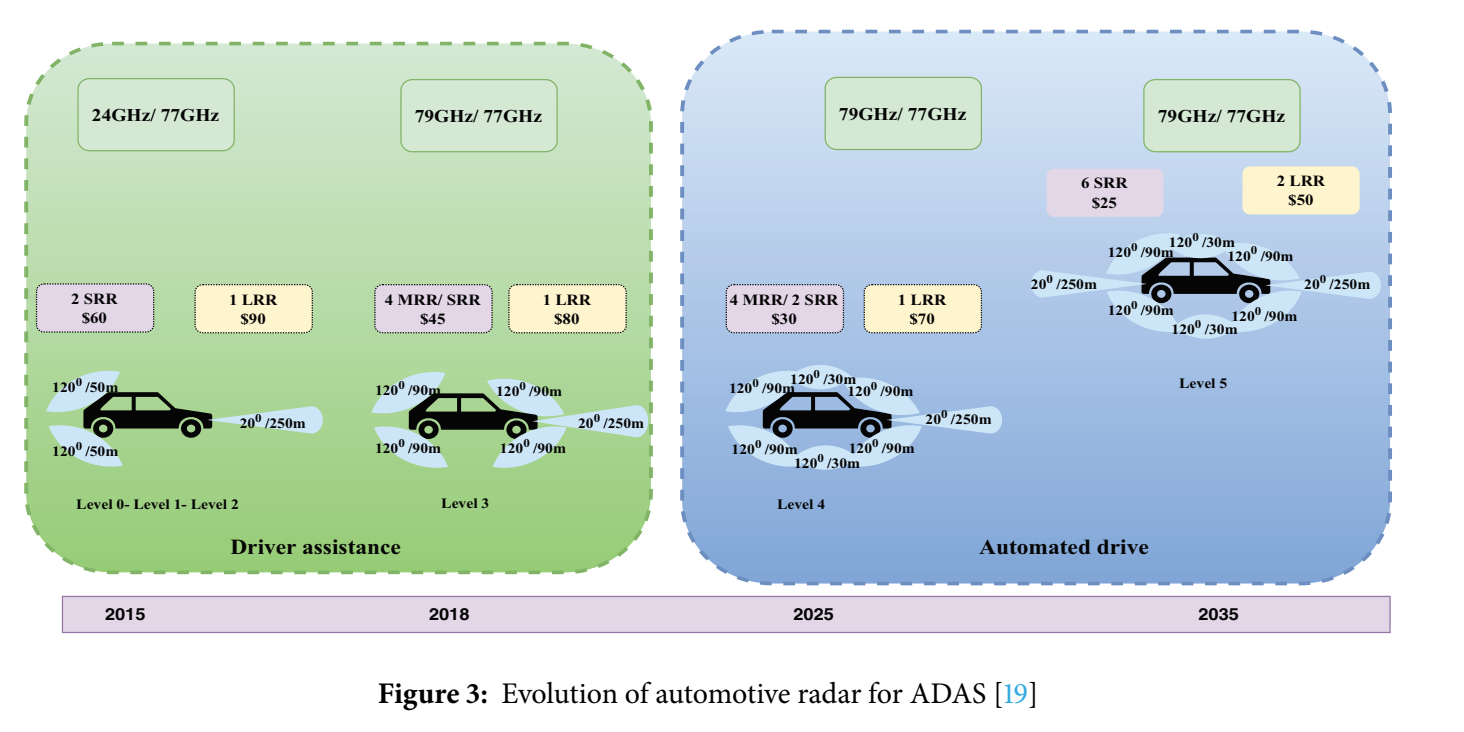
2015→2018→2025→2035 的演化可以总结为从"Driver assistance"走向"Automated drive",并标注不同阶段采用的频段组合(24/77/79 GHz),SRR/MRR/LRR 的数量变化与单价下降趋势(例如 LRR 从约 $90 逐步走向更低)。图中还用类似"120°/90 m""20°/250 m""120°/30 m"的标注表达不同雷达视场与量程。雷达越多、车流越密,互扰概率越高、目标越拥挤,要求更强的检测与角度分辨算法,反过来推动本文后续对 DOA、干扰抑制与跟踪的讨论。
3. FMCW 雷达基础数学:距离、速度与拍频的来源
3.1 从"线性调频发射"到"IF 拍频"
用上升 chirp 表达发射信号:
STx(t)=ATxcos(2πf0t+πkt2),t∈[0,Tch](1) S_{Tx}(t)=A_{Tx}\cos\left(2\pi f_0 t+\pi k t^2\right),\quad t\in[0,T_{ch}] \tag{1} STx(t)=ATxcos(2πf0t+πkt2),t∈[0,Tch](1)
其中 f0f_0f0 是起始频率,TchT_{ch}Tch 是一个 chirp 的持续时间,BBB 是扫频带宽,斜率 k=B/Tchk=B/T_{ch}k=B/Tch。
回波是延迟且衰减的叠加:
SRx(t)=∑i=1NATxαicos(2πf0(t−τi)+πk(t−τi)2)(2) S_{Rx}(t)=\sum_{i=1}^{N}A_{Tx}\alpha_i\cos\left(2\pi f_0 (t-\tau_i)+\pi k (t-\tau_i)^2\right) \tag{2} SRx(t)=i=1∑NATxαicos(2πf0(t−τi)+πk(t−τi)2)(2)
αi\alpha_iαi 代表路径损耗与反射损耗带来的幅度衰减,τi\tau_iτi 是第 iii 个点目标的往返时延。
接收端把 SRx(t)S_{Rx}(t)SRx(t) 与 STx(t)S_{Tx}(t)STx(t) 相乘并低通:
SIF(t)=[STx(t)⋅SRx(t)]∗hL(t)=∑i=1NAIF,icos(2πfB,it+θi)(3) S_{IF}(t)=\big[S_{Tx}(t)\cdot S_{Rx}(t)\big]*h_L(t) =\sum_{i=1}^{N}A_{IF,i}\cos(2\pi f_{B,i}t+\theta_i) \tag{3} SIF(t)=[STx(t)⋅SRx(t)]∗hL(t)=i=1∑NAIF,icos(2πfB,it+θi)(3)
两条 chirp 的相位相减后,剩下一个与 τi\tau_iτi 成正比的线性相位项,从而表现为一个低频(相对 RF)的拍频正弦。附录里会把从 (1)(2) 到 (3) 的三角恒等式/复包络推导写完整。
3.2 距离测量:拍频与时延/距离的线性关系
拍频:
fB,i=kτi=BTch⋅2dic(4) f_{B,i}=k\tau_i=\frac{B}{T_{ch}}\cdot \frac{2d_i}{c} \tag{4} fB,i=kτi=TchB⋅c2di(4)
其中 did_idi 是目标距离(文中此处用 did_idi 表示,后面也用 RRR 表示距离),ccc 为光速,τi=2di/c\tau_i=2d_i/cτi=2di/c。于是距离估计:
R=cτi2(5) R=\frac{c\tau_i}{2} \tag{5} R=2cτi(5)
把 (4)(5) 串起来,我们可以得到一个非常工程化的"FFT 距离标尺":
R=c2⋅fBk=c2⋅TchBfB. R=\frac{c}{2}\cdot\frac{f_B}{k} =\frac{c}{2}\cdot \frac{T_{ch}}{B}f_B. R=2c⋅kfB=2c⋅BTchfB.
因此快时间 FFT 的频率轴一旦确定,就能按上式直接映射为距离轴。
文章还给了最大无模糊距离:
Rmax=cTch2(6) R_{max}=\frac{cT_{ch}}{2} \tag{6} Rmax=2cTch(6)
它强调"回波来自当前 chirp 还是上一个 chirp"会引起距离歧义:当回波延迟过大时,dechirp 过程会把不同时刻的 chirp 混在一起,从而出现模糊。
距离分辨率:
Rreso=c2B(7) R_{reso}=\frac{c}{2B} \tag{7} Rreso=2Bc(7)
这条式子在雷达里几乎是"金科玉律":带宽越大,距离分辨率越好。附录我会把它从"拍频分辨率/傅里叶分辨率"角度再次推一遍。
3.3 速度测量:Doppler 如何进入 IF 信号与慢时间 FFT
文章用时间变化的往返时延刻画运动目标:
τi(t)=τ0,i+2vict(8) \tau_i(t)=\tau_{0,i}+\frac{2v_i}{c}t \tag{8} τi(t)=τ0,i+c2vit(8)
这相当于假设目标沿径向以速度 viv_ivi 匀速运动,则路径长度随时间线性变化,往返延迟也随时间线性变化。将其代入 IF 表达式后,IF 信号写成:
SIF(t)=∑i=1NAIF,icos(2π(fB,i+fD,i)t+θi)(9) S_{IF}(t)=\sum_{i=1}^{N}A_{IF,i}\cos\left(2\pi (f_{B,i}+f_{D,i})t+\theta_i\right) \tag{9} SIF(t)=i=1∑NAIF,icos(2π(fB,i+fD,i)t+θi)(9)
其中 Doppler 频率(文中写法):
fD,i=f02vic f_{D,i}=f_0\frac{2v_i}{c} fD,i=f0c2vi
也等价于 fD,i=2vi/λf_{D,i}=2v_i/\lambdafD,i=2vi/λ。随后给出基于 chirp 间相位差估计速度的公式:
v=λ Δθ4πTch(10) v=\frac{\lambda\,\Delta\theta}{4\pi T_{ch}} \tag{10} v=4πTchλΔθ(10)
以及两目标的对应表达:
v1=λϕ14πTch,v2=λϕ24πTch(11) v_1=\frac{\lambda\phi_1}{4\pi T_{ch}},\qquad v_2=\frac{\lambda\phi_2}{4\pi T_{ch}} \tag{11} v1=4πTchλϕ1,v2=4πTchλϕ2(11)
这里 Δθ\Delta\thetaΔθ 与 ϕ\phiϕ 都是在强调"相邻 chirp 的相位差 "。它背后的关键关系是:慢时间采样间隔约为 TchT_{ch}Tch(或 PRI),若慢时间序列相位以 2πfD2\pi f_D2πfD 每秒推进,则相邻采样相位差 Δθ≈2πfDTch\Delta\theta \approx 2\pi f_D T_{ch}Δθ≈2πfDTch,再代入 fD=2v/λf_D=2v/\lambdafD=2v/λ 即得 (10)。附录中会把这一步写得更细,并解释为什么很多工程实现更倾向于做 Range-Doppler map(即慢时间 FFT)而不是直接用两帧相位差。
速度分辨率:
vreso=λ2Tf(12) v_{reso}=\frac{\lambda}{2T_f} \tag{12} vreso=2Tfλ(12)
TfT_fTf 是 chirp frame 的时长,直观上相当于慢时间观测时长;观测越久,Doppler 频率分辨率越高,映射到速度分辨率也越高(即重要的时频分辨率关系)。
Fig. 4:FMCW 的时频几何关系与拍频的可视化
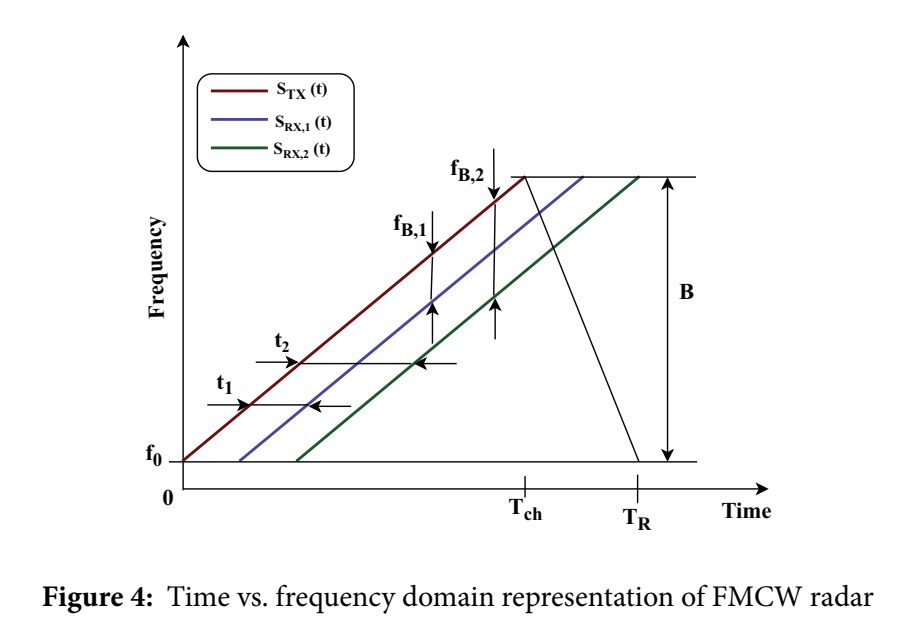
这幅时频图用一条红色斜线表示发射 chirp STX(t)S_{TX}(t)STX(t),两条不同延时的回波 SRX,1(t)S_{RX,1}(t)SRX,1(t)、SRX,2(t)S_{RX,2}(t)SRX,2(t) 用蓝/绿线表示。图中在两个时刻 t1,t2t_1,t_2t1,t2 画出发射与回波瞬时频率差,并标注 fB,1,fB,2f_{B,1},f_{B,2}fB,1,fB,2。我们可以直接从几何上读出:延时越大,发射线与回波线在同一时刻的频差越大,因此拍频越大,目标距离越远。图里还标出了扫频带宽 BBB、chirp 时长 TchT_{ch}Tch 和 chirp 重复周期 TRT_RTR,这些都是系统设计时决定分辨率与无模糊范围的关键参数。
4. 波形谱系与"距离---速度"解耦:CW、脉冲 CW、线性 FMCW、Fast chirp、OFDM、PMCW
文章在第 2.4 节把车载雷达波形分为连续波、脉冲类与调制类(FMCW/OFDM/PMCW),并强调波形选择会直接影响距离/速度/角度分辨率与抗干扰能力。
Fig. 5:连续波 vs 脉冲连续波的时间包络差异
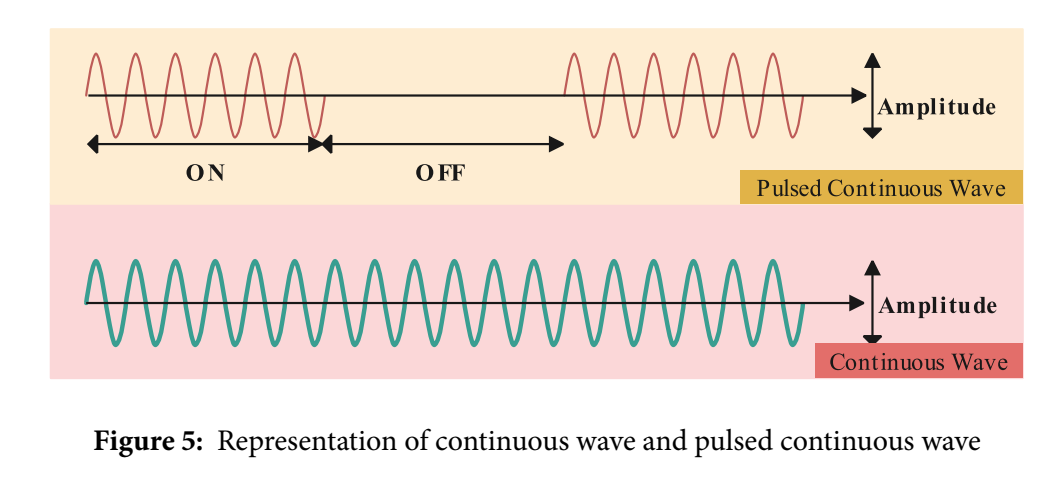
图的下半部分是 Continuous Wave:波形持续不断,天然适合从 Doppler 直接读速度,但因为没有明显的"发射---接收时间窗",很难从时间延迟直接得到距离(文章在 2.4.1 也直言"measuring the delay ... is challenging")。上半部分是 Pulsed Continuous Wave:用 ON/OFF 门控把连续波切成脉冲串,使得在 OFF 区间可以接收回波,因此更容易做距离/速度设计权衡(PRF 与脉冲宽度决定无模糊速度/距离与分辨率)。
4.1 线性 FMCW 的"上下坡"拍频
单目标 beat frequency 可以被分解成"Doppler 频移项 fdf_dfd"与"由距离引起的频率项 fbf_bfb":
fd=2λvr(13) f_d=\frac{2}{\lambda}v_r \tag{13} fd=λ2vr(13)
fb=2RcBsweepTs(14) f_b=\frac{2R}{c}\frac{B_{sweep}}{T_s} \tag{14} fb=c2RTsBsweep(14)
其中 vrv_rvr 是径向速度,BsweepB_{sweep}Bsweep 为扫频带宽,TsT_sTs 为 sweep time。
上坡与下坡的两个拍频:
fbu=fb−fd(15) f_{bu}=f_b-f_d \tag{15} fbu=fb−fd(15)
fbd=fb+fd(16) f_{bd}=f_b+f_d \tag{16} fbd=fb+fd(16)
距离项 fbf_bfb 对上下坡同号,而多普勒项 fdf_dfd 符号相反,因此一加一减就能解耦。文章直接写出距离与速度估计式:
R=cTs4Bsweep(fbd+fbu)(17) R=\frac{cT_s}{4B_{sweep}}( f_{bd}+f_{bu}) \tag{17} R=4BsweepcTs(fbd+fbu)(17)
vr=λ4(fbd−fbu)(18) v_r=\frac{\lambda}{4}( f_{bd}-f_{bu}) \tag{18} vr=4λ(fbd−fbu)(18)
它本质上就是线性方程组的求解:{fbu,fbd}\{f_{bu},f_{bd}\}{fbu,fbd} 是观测,{fb,fd}\{f_b,f_d\}{fb,fd} 是未知,两个方程解两个未知。
Fig. 6:时频图展示 fbuf_{bu}fbu 与 fbdf_{bd}fbd 的生成机制
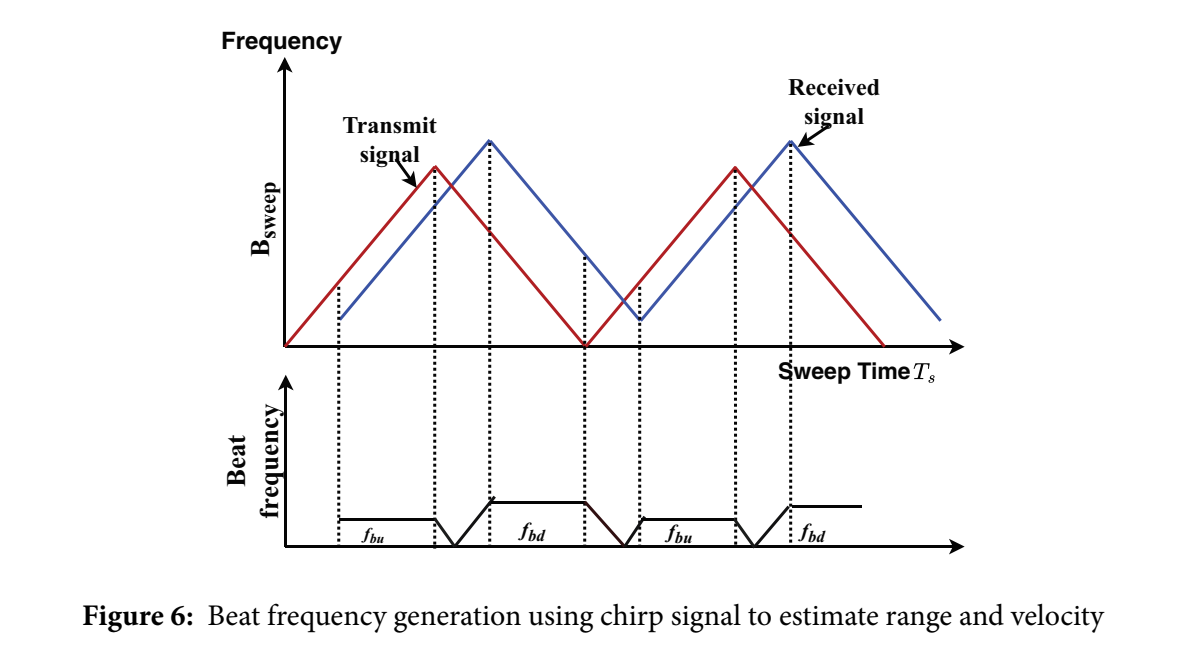
图中把"Transmit signal"与"Received signal"的扫频斜线画在同一坐标中,并把"Beat frequency"分段画出,标注了上坡 beat fbuf_{bu}fbu 与下坡 beat fbdf_{bd}fbd。从图形上看,beat frequency 就是"同一时刻发射与接收瞬时频率的差",而上下坡让这种差呈现不同的符号组合,从而对应式 (15)(16) 的加减结构。
4.2 Fast chirp ramp sequence:为什么强调"2D-FFT 先每 chirp 后跨 chirp"
文章在 2.4.4 指出 fast chirp waveform 的优势之一是:2D-FFT 处理更准确地得到距离与速度,并且"targets 的 beat frequency 高于噪声拐点频率(noise corner frequency)",对弱目标的 SNR 有利。
Fig. 7:fast chirp 的时频示例
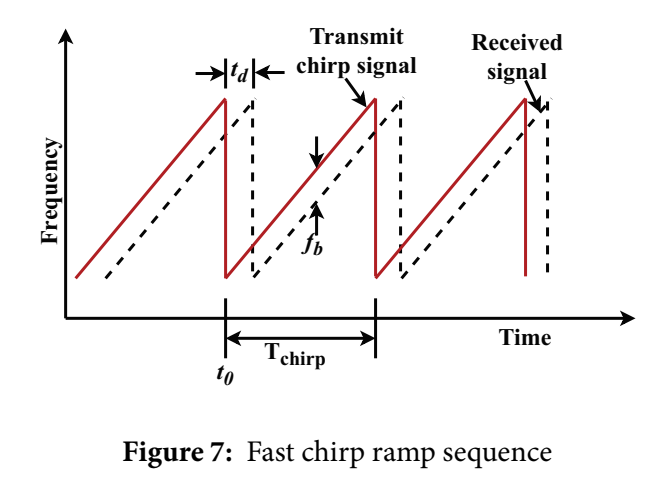
图中横轴 Time,纵轴 Frequency,分别画出 Transmit 与 Received 的 chirp 斜线。标注了 TchirpT_{chirp}Tchirp、t0t_0t0、以及与目标距离相关的延迟 tdt_dtd 与拍频 fbf_bfb。它在图形层面强调:短 chirp 周期 + 频率快速爬坡会改变 beat 信号的频谱分布,使得距离/速度估计更适合用"先 Range-FFT 再 Doppler-FFT"的标准 2D-FFT 流程。
4.3 OFDM 与 PMCW:数字化与抗干扰的两条路径
文章对 OFDM 的描述强调其"子载波正交、FFT 解调便利、用频域信道估计得到距离像",并提醒 Doppler 造成 ICI,因此子载波间隔需大于最大 Doppler。
对 PMCW,作者给出二进制相位编码的发射模型:
STx(t)=∑r=0R−1g(t−rTch)cos(2πf0t+Irπ)(19) S_{Tx}(t)=\sum_{r=0}^{R-1} g(t-rT_{ch})\cos(2\pi f_0 t + I_r\pi) \tag{19} STx(t)=r=0∑R−1g(t−rTch)cos(2πf0t+Irπ)(19)
其中 Ir∈{0,1}I_r\in\{0,1\}Ir∈{0,1} 表示 0/π 相位映射,g(⋅)g(\cdot)g(⋅) 是门控函数(只在单个码片/符号区间内为 1)。接收模型:
SRx=ATxST(t−τd)exp(j2πfdt)(20) S_{Rx}=A_{Tx} S_T(t-\tau_d)\exp(j2\pi f_d t) \tag{20} SRx=ATxST(t−τd)exp(j2πfdt)(20)
距离通过"接收与发射码的相关"得到;对每个距离 bin 做 FFT 得 Doppler,用于速度估计。但是PMCW 的工程代价也很明显:必须覆盖全带宽采样,对高速高分辨 ADC 需求更高,但优势是更强的互扰抑制潜力与更小的 range-Doppler 耦合倾向(文章在 2.4.7 前后也强调 PMCW 趋势)。
4.4 波形选择的可计算指标表格
Table 2:不同车载雷达波形特性对比
| Feature | CW | FMCW Chirp | OFDM | PMCW |
|---|---|---|---|---|
| Principle | Measures Doppler shift | Frequency modulation for range and velocity | Uses orthogonal frequency subcarriers | Uses phase modulation for interference resistance |
| Range measurement | Difficult to determine | Achievable via frequency shift | Good due to multi-tone processing | Achievable via phase modulation / correlation |
| Velocity measurement | Direct from Doppler shift | Estimated from beat frequency | Extracted from chirp rate and Doppler shift | Achievable using phase shifts (per range bin FFT) |
| Interference resistance | Low | Moderate | High (due to orthogonality) | High (due to phase coding) |
| Computational complexity | Low | Moderate | High | High |
| Antenna requirement | Separate Tx/Rx antennas | Single antenna with TDM (typical) | Single antenna (system-dependent) | Multiple antennas often required |
| Applications | Speed measurement | ADAS, collision avoidance | High-resolution automotive radar | Short-range automotive radar |
CW 的速度测量最直接但距离最难;FMCW 用拍频让距离很自然,同时用慢时间让速度也自然,复杂度中等;OFDM 与 PMCW 都更数字化、更容易做正交与编码以提升抗干扰,但在 ICI(OFDM)或高速采样(PMCW)上付出代价。车载主流长期偏爱 FMCW 的原因也就很清晰:它在距离/速度的可测性、硬件复杂度与实时性之间,提供了一个最平衡的"工程解"。
Table 3:不同波形分辨率表达
| Type of waveforms | Resolution | Properties |
|---|---|---|
| Continuous wave | Δfd=1/T\Delta f_d=1/TΔfd=1/T | No accurate range resolution |
| Pulsed CW | ΔR=cTp2\Delta R=\frac{cT_p}{2}ΔR=2cTp, Δfd=1/Tp\Delta f_d=1/T_pΔfd=1/Tp | Range-Doppler trade-off |
| FMCW | ΔR=c2B\Delta R=\frac{c}{2B}ΔR=2Bc, Δfd=1/(PT0)\Delta f_d=1/(PT_0)Δfd=1/(PT0) | Range and Doppler information |
| Fast chirp ramp | ΔR=c2B\Delta R=\frac{c}{2B}ΔR=2Bc, vreso=λ/(2Tf)v_{reso}=\lambda/(2T_f)vreso=λ/(2Tf) | 2D-FFT provides accurate Range & Doppler |
| OFDM | ΔR=cNΔf\Delta R=\frac{c}{N\Delta f}ΔR=NΔfc, Δfd=1/(PTN)\Delta f_d=1/(PT_N)Δfd=1/(PTN) | Digital radar; two independent dimensions |
| PMCW | ΔR=c2fclk\Delta R=\frac{c}{2f_{clk}}ΔR=2fclkc, Δf=Fs/NPRBS\Delta f=F_s/N_{PRBS}Δf=Fs/NPRBS | Digital coded radar |
| Combined FSK + FMCW | ΔR=c2B\Delta R=\frac{c}{2B}ΔR=2Bc, Δfd=1/(PT0)\Delta f_d=1/(PT_0)Δfd=1/(PT0) | Max range decided by Δf\Delta fΔf |
这张表在工程上最有用的是:把"分辨率"直接写成设计变量的函数。比如 FMCW/fast chirp 的 ΔR\Delta RΔR 只跟 BBB 相关,意味着提高距离分辨率首先要争取更大带宽;速度分辨率跟 TfT_fTf 或观测时长相关,意味着想分清更小速度差就要更长的慢时间积累,但这会牺牲刷新率与实时性。OFDM 的距离分辨率与 NΔfN\Delta fNΔf 相关,说明它的"有效带宽"来自子载波数量与间隔;PMCW 的距离分辨率与码速 fclkf_{clk}fclk 相关,如果想要更细距离,就要更高码率与更强 ADC。
5. 互扰建模:把"其他雷达的扫频"变成 INR/PSD(式 (21)--(24))
文章在 2.5 节从 INR(Interference-to-Noise Ratio)切入,强调互扰强弱取决于车距、双方波形、以及受害雷达的解调/带通处理方式。它给出在受害雷达处的干扰功率谱密度:
$$
\mathrm{PSD}_{int}
\Bigg[\frac{P_t G_T \lambda L_{Tx}L_f N_{Tx}}{B(4\pi R^2)}\Bigg]
\Bigg[\frac{G_R \lambda L_{Rx}L_f N_{Rx}}{4\pi}\Bigg]
(D_f)(K_{FMCW})
\frac{P_t G_T L_{Tx}L_f N_{Tx}\lambda^2 G_R L_{Rx}L_f N_{Rx}}{B(4\pi R)^2}
(D_f)(K_{FMCW})
\tag{21}
这个式子可以从"Friis 传播 + 带宽归一 + 调制映射"来理解:PtP_tPt 经过传播损耗 (4πR)−2(4\\pi R)\^{-2}(4πR)−2 与波长项 λ2\\lambda\^2λ2 到达受害雷达,再乘双方天线增益与损耗(包括车身 fascia 的 LfL_fLf),最后除以 BBB 得到"每 Hz 的功率密度"。Df∈\[0,1\]D_f\\in\[0,1\]Df∈\[0,1\] 则描述干扰雷达在受害雷达驻留时间/频带内"撞上"的时间占比。最关键的调制相关系数是 KFMCWK_{FMCW}KFMCW,文章把它定义为 RF 干扰 PSD 与基带干扰 PSD 的映射: ##
K_{FMCW}
\frac{\mathrm{PSD}_{Bb}I}{\mathrm{PSD}_{RF}I}
\frac{\Delta F_{RF}^I}{\Delta F_{Bb}^I}
\tag{22}
这意味着同样的干扰能量,如果经过去调制/滤波后被压缩进更窄的基带带宽 ΔFBbI\\Delta F_{Bb}\^IΔFBbI,那么基带 PSD 会更高,受害更严重。对 FMCW-FMCW 互扰,文章给出两种典型对齐方式下的 KFMCWK_{FMCW}KFMCW: 当两者 sweep 的时长、起始频率、起始时间相同(Type A): KFMCW=∣SwISwV−SwI∣(23) K_{FMCW}=\\left\|\\frac{S_w\^I}{S_w\^V-S_w\^I}\\right\| \\tag{23} KFMCW= SwV−SwISwI (23) 当两者 sweep 的时长、起始时间、中心频率相同(Type B): KFMCW=2∣SwISwV−SwI∣(24) K_{FMCW}=2\\left\|\\frac{S_w\^I}{S_w\^V-S_w\^I}\\right\| \\tag{24} KFMCW=2 SwV−SwISwI (24) SwI,SwVS_w\^I,S_w\^VSwI,SwV 是干扰雷达与受害雷达的扫频斜率。我们可以直接看到一个非常敏感的结构:当两者斜率很接近时,分母变小,KFMCWK_{FMCW}KFMCW 急剧增大,意味着"参数相似的车载雷达更容易强烈互扰"。附录会用"下变频后的干扰扫过接收带通的时间宽度"把 (23)(24) 的比例结构再推一遍。 文章随后讨论 PMCW-PMCW 与 FMCW-PMCW 的互扰特征,强调它们更像"噪声型宽带干扰",会抬高噪声底。缓解方式分发射端(跳频、时序抖动等让不同雷达在时频/极化域更"正交")与接收端(时域剔除、匹配滤波积分增益、CDMA 码分离、自适应滤波甚至神经网络分离重构)。 *** ** * ** *** ### 6. 检测:从 4D 数据模型到 4D-FFT,再到 CFAR 阈值 #### 6.1 4D 基带数据模型:目标在快时间/慢时间/空间维都是复指数 3.1 节给出单发射、多接收的基带模型: xm,r(t)=∑i=1NAiS(t−τi)exp(j2πfd,irTc)exp(j2πfcΔτi,m)+vm,r(t)(25) x_{m,r}(t)= \\sum_{i=1}\^{N}A_i S(t-\\tau_i)\\exp(j2\\pi f_{d,i} rT_c)\\exp(j2\\pi f_c \\Delta\\tau_{i,m}) +v_{m,r}(t) \\tag{25} xm,r(t)=i=1∑NAiS(t−τi)exp(j2πfd,irTc)exp(j2πfcΔτi,m)+vm,r(t)(25) 这条式子几乎是后续所有"高维 FFT/阵列处理"的基础: 快时间 ttt 上的 S(t−τi)S(t-\\tau_i)S(t−τi) 负责距离信息;慢时间(跨 chirp 索引 rrr)上的 exp(j2πfd,irTc)\\exp(j2\\pi f_{d,i} rT_c)exp(j2πfd,irTc) 负责 Doppler;阵元索引 mmm 上通过 Δτi,m\\Delta\\tau_{i,m}Δτi,m 编码角度信息;vm,r(t)v_{m,r}(t)vm,r(t) 是加性噪声。 将接收与发射信号共轭相乘得到 dechirp 后的表达: ##
\tilde x_{m,r}(t)
\sum_{i=1}^{N}\tilde A_i
\exp(-j2\pi B\tau_i)
\exp(j2\pi T f_{d,i}r)
\exp(j2\pi f_c\Delta\tau_{i,m})
+\tilde v_{m,r}(t)
\tag{26}
在均匀平面阵列(水平/垂直阵元)下,空间时延对阵元索引近似线性,因此整个数据就成为"多个维度的正弦/复指数乘积"。这正是多维 FFT 能够把目标在各维分离开的原因。 #### 6.2 4D FFT:把距离/速度/方位/俯仰同时拉开 采样得到 x\[l,r,m\]=x\~m,r(lTs)x\[l,r,m\]=\\tilde x_{m,r}(lT_s)x\[l,r,m\]=x\~m,r(lTs),对快时间、慢时间与两维阵元做 FFT/波束扫描,文章写出 4D FFT: X\[p,q,θ,ϕ\]=∑mv=1M∑mh=1M∑r=1R∑l=1Lx\[l,r,m\] e−j2πplL e−j2πqrR⋅ej2πdaλmhsinθcosϕ ej2πdaλmvsinϕ(27) \\begin{aligned} X\[p,q,\\theta,\\phi\] =\& \\sum_{m_v=1}\^{M}\\sum_{m_h=1}\^{M}\\sum_{r=1}\^{R}\\sum_{l=1}\^{L} x\[l,r,m\]\\, e\^{-j2\\pi p\\frac{l}{L}}\\, e\^{-j2\\pi q\\frac{r}{R}} \\\\ \&\\cdot e\^{j2\\pi\\frac{d_a}{\\lambda} m_h\\sin\\theta\\cos\\phi}\\, e\^{j2\\pi\\frac{d_a}{\\lambda} m_v\\sin\\phi} \\end{aligned} \\tag{27} X\[p,q,θ,ϕ\]=mv=1∑Mmh=1∑Mr=1∑Rl=1∑Lx\[l,r,m\]e−j2πpLle−j2πqRr⋅ej2πλdamhsinθcosϕej2πλdamvsinϕ(27) 这里 ppp 与 lll 对应距离维(快时间 FFT),qqq 与 rrr 对应速度维(慢时间 FFT),θ,ϕ\\theta,\\phiθ,ϕ 则对应方位/俯仰角(空间维 FFT 或等价的波束扫描),dad_ada 为阵元间距。附录会把"从模型 (25)(26) 到 (27)"的离散化与物理参数映射关系再写得更细,包括 ppp 如何对应拍频 fBf_BfB,以及拍频如何再映射为距离 RRR。 #### 6.3 CFAR 检测:用局部噪声估计实现"恒虚警" 目标在至少一个维度上可分离后,就可以在 Range-Doppler 或 Range-Angle 等域用 CFAR 检测。 CA-CFAR 的判决不等式如下:
|X[p,q,\theta,\phi]|^2
T_{CFAR}+\sigma_{nv}^2[p,q,\theta,\phi],
\quad \forall p,q,\theta,\phi
\tag{28}
其中 σnv2\\sigma_{nv}\^2σnv2 由 CUT 周围的训练单元估计得到,TCFART_{CFAR}TCFAR 是与虚警概率相关的门限偏置。 #### Fig. 8:CA-CFAR 窗口结构与阈值生成 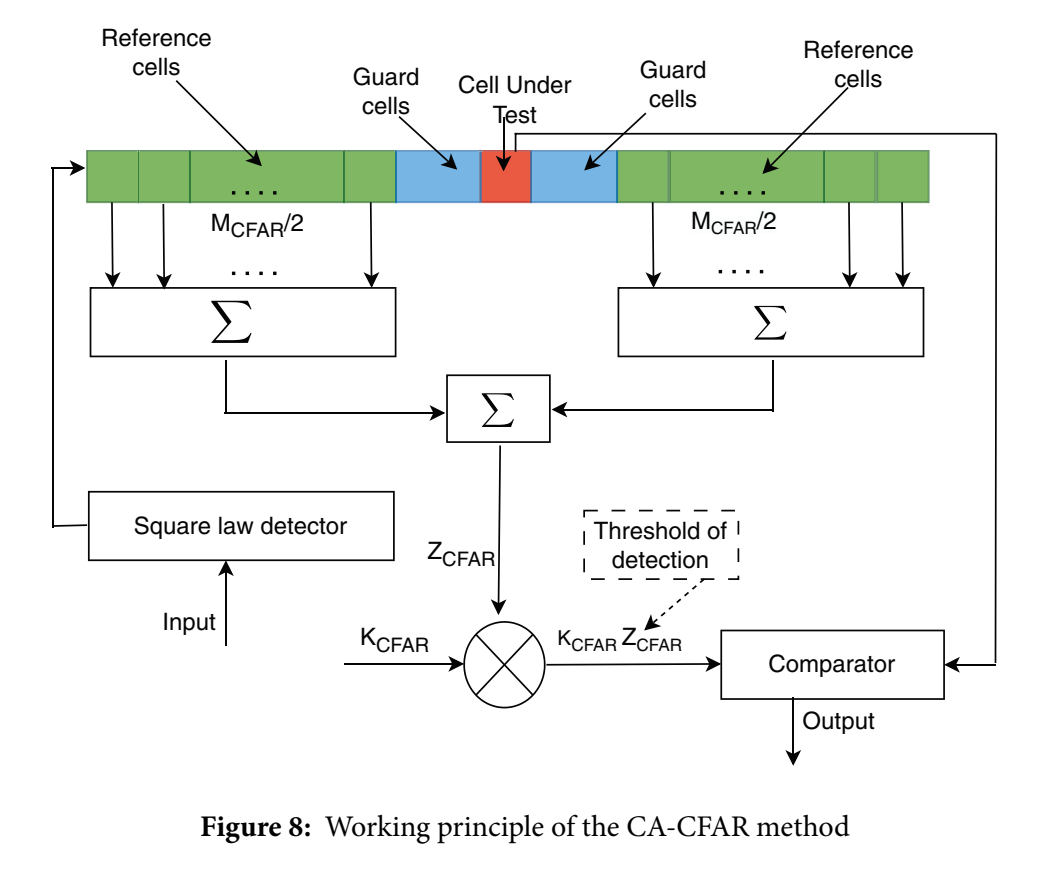 图中间红色块是 Cell Under Test(CUT),紧邻两侧蓝色块是 Guard cells(保护单元,用来防止目标泄漏污染噪声估计),更外侧绿色块是 Reference cells(训练单元)。训练单元经过求和/平均得到 ZCFARZ_{CFAR}ZCFAR,再乘以 KCFARK_{CFAR}KCFAR 得检测阈值,最后与 CUT 的平方律检测输出比较,产生检测结果。图里还画出"Square law detector""Comparator""Threshold of detection"等模块,使得 CA-CFAR 的实现结构非常直观。 作者随后给出 GOCA/SOCA/OS-CFAR 的阈值选取差异,并提供对比表。 **Table 4:CFAR 技术对比** | Type | Method of threshold detection | Advantages | Disadvantages | |-----------|-------------------------------------------------|------------------------------------------|----------------------------------------------| | CA-CFAR | Average power of neighboring cells as threshold | High SNR in uniform noise | Not beneficial for multiple target detection | | GOCA-CFAR | Two windows; take the larger mean as threshold | Good false alarm control in clutter | Not beneficial for multiple target detection | | SOCA-CFAR | Two windows; take the smaller mean as threshold | Beneficial for multiple target detection | Higher false alarm rate | | OS-CFAR | Sort training cells; pick one order statistic | Beneficial for multiple target detection | Longer computation duration | 注意 SOCA 的"更适合多目标"与"更高虚警率"是同一枚硬币的两面:它倾向于用较小均值作为噪声估计,从而降低阈值,提升检测灵敏度,但会增加误检风险。OS-CFAR 通过排序取分位数提升多目标鲁棒性,但排序代价更高。附录里会补上一个车载雷达里很常用但本文未写出的关键推导:在噪声服从指数分布(幅度平方为指数、功率为指数)的假设下,CA-CFAR 的 KCFARK_{CFAR}KCFAR 如何由期望虚警概率 PFAP_{FA}PFA 推导得到。 *** ** * ** *** ### 7. DOA(到达角)估计:从阵列几何到 Bartlett/MVDR/MUSIC/ESPRIT 的"数学骨架" #### Fig. 9:DOA 方法分类树 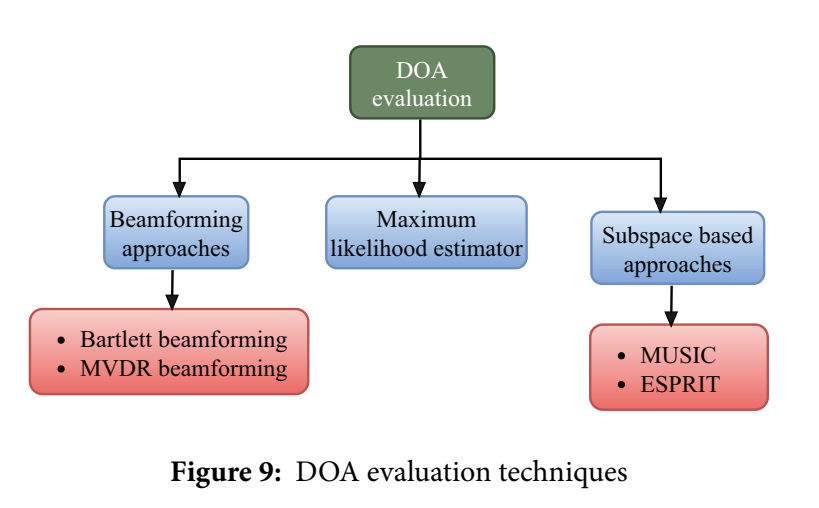 图把 DOA evaluation 分为 beamforming approaches(Bartlett、MVDR)、maximum likelihood estimator、subspace based approaches(MUSIC、ESPRIT)。本文重点展开 Bartlett/MVDR/MUSIC/ESPRIT,并在 Table 5 对比复杂度与分辨率。 #### Fig. 10:ULA 入射波前与阵元相位差示意 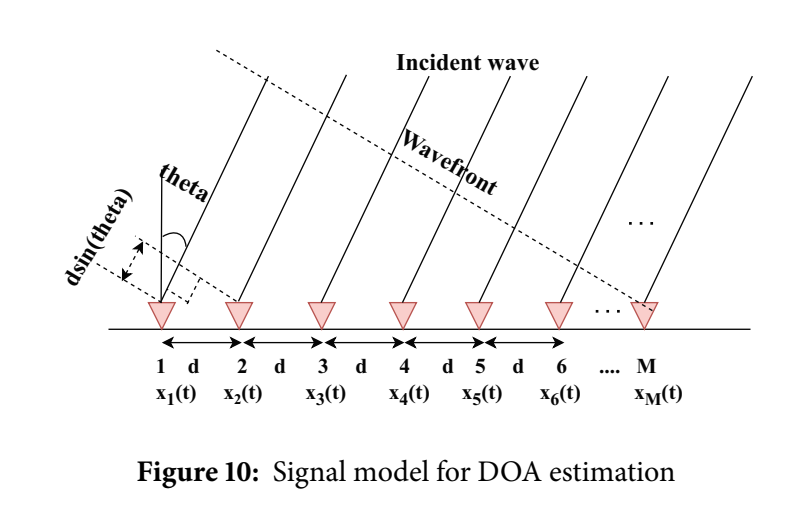 图中一列均匀线阵(标注 1d、2d、...、M)接收同一入射波前,阵元间距为 ddd,入射角为 θ\\thetaθ,几何路径差为 dsinθd\\sin\\thetadsinθ。这直接决定了相邻阵元接收信号的相位差 Δφ=2π(dsinθ)/λ\\Delta\\varphi = 2\\pi(d\\sin\\theta)/\\lambdaΔφ=2π(dsinθ)/λ,从而导向矢量呈指数序列。 #### 7.1 统一阵列模型与协方差:所有 DOA 算法共同的出发点 给出阵列接收模型: X(t)=A(θ)S(t)+N(t)(29) X (t) = A(\\theta) S (t) + N (t) \\tag{29} X(t)=A(θ)S(t)+N(t)(29) 其中 X(t)∈CM×1X(t)\\in\\mathbb C\^{M\\times 1}X(t)∈CM×1 是阵列观测,A(θ)∈CM×ktA(\\theta)\\in\\mathbb C\^{M\\times k_t}A(θ)∈CM×kt 是由各目标导向矢量组成的 steering matrix,S(t)∈Ckt×1S(t)\\in\\mathbb C\^{k_t\\times 1}S(t)∈Ckt×1 为源信号,N(t)N(t)N(t) 为噪声(方差 σ2\\sigma\^2σ2)。ULA 的导向矢量写为: a(θi)=\[1,e−j2πdsin(θi)/λ,...,e−j2πd(N−1)sin(θi)/λ\]T(30) a (θ_i)=\\left\[1, e\^{-j2\\pi d\\sin(\\theta_i)/\\lambda}, \\ldots, e\^{-j2\\pi d (N-1)\\sin(\\theta_i)/\\lambda}\\right\]\^T \\tag{30} a(θi)=\[1,e−j2πdsin(θi)/λ,...,e−j2πd(N−1)sin(θi)/λ\]T(30) 然后引入加权合成: Y(t)=wHX(t)(31) Y(t)=w\^H X(t) \\tag{31} Y(t)=wHX(t)(31) 输出功率: P(w)=E\[∣y(t)∣2\]=wHE\[XXH\]w=wHRcmw(32) P(w)=\\mathbb E\[\|y(t)\|\^2\]=w\^H\\mathbb E\[XX\^H\]w=w\^H R_{cm} w \\tag{32} P(w)=E\[∣y(t)∣2\]=wHE\[XXH\]w=wHRcmw(32) 这四条式子奠定了两类路线:波束形成类算法通过选权向量 www 直接塑形波束;子空间类算法通过分析 RcmR_{cm}Rcm 的特征结构(信号子空间与噪声子空间)实现超分辨 DOA。 #### 7.2 Bartlett:用 w=a(θ)w=a(\\theta)w=a(θ) 扫描功率谱 Bartlett(常规波束形成)取权向量 w=a(θ)w=a(\\theta)w=a(θ),空间功率谱: Pbart(θ)=aH(θ)Rcma(θ)aH(θ)a(θ)(33) P_{bart}(\\theta)= \\frac{a\^H(\\theta)R_{cm}a(\\theta)}{a\^H(\\theta)a(\\theta)} \\tag{33} Pbart(θ)=aH(θ)a(θ)aH(θ)Rcma(θ)(33) 它的主瓣宽度受阵列孔径限制,多目标近角分辨能力较弱,文章也明确写出其"多源低分辨率"的局限。 #### 7.3 MVDR:约束最小方差推到闭式解 MVDR(最小方差无失真响应)用约束优化刻画:在目标方向保持单位响应,同时让输出功率最小: minP(w)=wHRcmws.t.wHa(θ)=1(34) \\min P(w)=w\^H R_{cm} w \\quad \\text{s.t.}\\quad w\^H a(\\theta)=1 \\tag{34} minP(w)=wHRcmws.t.wHa(θ)=1(34) 其权向量闭式解: wMVDR=Rcm−1a(θ)aH(θ)Rcm−1a(θ)(35) w_{MVDR}=\\frac{R_{cm}\^{-1}a(\\theta)}{a\^H(\\theta)R_{cm}\^{-1}a(\\theta)} \\tag{35} wMVDR=aH(θ)Rcm−1a(θ)Rcm−1a(θ)(35) 对应功率谱: PMVDR(θ)=1aH(θ)Rcm−1a(θ)(36) P_{MVDR}(\\theta)=\\frac{1}{a\^H(\\theta)R_{cm}\^{-1}a(\\theta)} \\tag{36} PMVDR(θ)=aH(θ)Rcm−1a(θ)1(36) 这比 Bartlett 更能压制干扰,但对协方差估计误差敏感,且矩阵求逆带来高复杂度。附录会把从 (34) 到 (35) 的拉格朗日推导补充完整。 #### 7.4 MUSIC:噪声子空间正交性与伪谱峰 协方差模型: Rcm=A(θ)RsAH(θ)+σ2I(37) R_{cm}=A(\\theta)R_sA\^H(\\theta)+\\sigma\^2 I \\tag{37} Rcm=A(θ)RsAH(θ)+σ2I(37) 并进行特征分解: Rcm=UΛUH(38) R_{cm}=U\\Lambda U\^H \\tag{38} Rcm=UΛUH(38) 特征值排序: λ1≥⋯≥λKt\>λKt+1=⋯=λM=σ2(39) \\lambda_1 \\ge \\cdots \\ge \\lambda_{K_t} \> \\lambda_{K_t+1}=\\cdots=\\lambda_M=\\sigma\^2 \\tag{39} λ1≥⋯≥λKt\>λKt+1=⋯=λM=σ2(39) 定义信号子空间与噪声子空间: Us=\[u1,...,uKt\],Un=\[uKt+1,...,uM\](40--41) U_s=\[u_1,\\ldots,u_{K_t}\],\\qquad U_n=\[u_{K_t+1},\\ldots,u_M\] \\tag{40--41} Us=\[u1,...,uKt\],Un=\[uKt+1,...,uM\](40--41) 核心正交关系: aH(θkt)Un=0T(42) a\^H(\\theta_{k_t})U_n=0\^T \\tag{42} aH(θkt)Un=0T(42) 因此当 θ\\thetaθ 扫到真实 DOA 时,有: aH(θ)UnUnHa(θ)≈0(43) a\^H(\\theta)U_nU_n\^H a(\\theta)\\approx 0 \\tag{43} aH(θ)UnUnHa(θ)≈0(43) MUSIC 伪谱: PMUSIC(θ)=1aH(θ)UnUnHa(θ)(44) P_{MUSIC}(\\theta)=\\frac{1}{a\^H(\\theta)U_nU_n\^H a(\\theta)} \\tag{44} PMUSIC(θ)=aH(θ)UnUnHa(θ)1(44) 分母越接近 0,伪谱越高,从而形成尖锐谱峰,实现超分辨。它的代价是需要源数 KtK_tKt 的先验/估计,并且要做角度谱搜索;加上 EVD,使得复杂度与延迟在车载实时系统里成为压力。 #### 7.5 ESPRIT:用"平移不变性"绕开角度搜索 ESPRIT 的关键是假设阵列由两个重叠的平移子阵构成。文章构造两个子阵输出: xe1(t)=Je1x(t),xe2(t)=Je2x(t)(45--46) x_{e1}(t)=J_{e1}x(t),\\qquad x_{e2}(t)=J_{e2}x(t) \\tag{45--46} xe1(t)=Je1x(t),xe2(t)=Je2x(t)(45--46) 其中选择矩阵: Je1=\[IM−1 0\],Je2=\[0 IM−1\] J_{e1}=\[I_{M-1}\\ \\ 0\],\\qquad J_{e2}=\[0\\ \\ I_{M-1}\] Je1=\[IM−1 0\],Je2=\[0 IM−1\] 于是 xe1(t)=A1s(t)+n1(t)(47) x_{e1}(t)=A_1 s(t) + n_1(t) \\tag{47} xe1(t)=A1s(t)+n1(t)(47) xe2(t)=A2s(t)+n2(t)(48) x_{e2}(t)=A_2 s(t) + n_2(t) \\tag{48} xe2(t)=A2s(t)+n2(t)(48) 并满足平移不变关系: A2=A1Φ,Φ=diag(ejψ1,...,ejψK)(49) A_2=A_1\\Phi,\\quad \\Phi=\\mathrm{diag}(e\^{j\\psi_1},\\ldots,e\^{j\\psi_K}) \\tag{49} A2=A1Φ,Φ=diag(ejψ1,...,ejψK)(49) 随后用快拍数据矩阵与样本协方差: Xe=\[xe(1),...,xe(Nes)\]∈CM×Nes(50) X_e=\[x_e(1),\\ldots,x_e(N_{es})\]\\in\\mathbb C\^{M\\times N_{es}} \\tag{50} Xe=\[xe(1),...,xe(Nes)\]∈CM×Nes(50) R\^cm=1NesXeXeH(51) \\hat R_{cm}=\\frac{1}{N_{es}}X_e X_e\^H \\tag{51} R\^cm=Nes1XeXeH(51) EVD 得到信号子空间: R\^cm=UsΛsUsH+UnΛnUnH(52) \\hat R_{cm}=U_s\\Lambda_sU_s\^H+U_n\\Lambda_nU_n\^H \\tag{52} R\^cm=UsΛsUsH+UnΛnUnH(52) 拆分 UsU_sUs: U1=Je1Us,U2=Je2Us(53--54) U_1=J_{e1}U_s,\\qquad U_2=J_{e2}U_s \\tag{53--54} U1=Je1Us,U2=Je2Us(53--54) 并设: U2=U1Ψ(55) U_2=U_1\\Psi \\tag{55} U2=U1Ψ(55) 最小二乘解: Ψ=U1†U2(56) \\Psi=U_1\^\\dagger U_2 \\tag{56} Ψ=U1†U2(56) 特征分解: Ψvkt=λktvkt(57) \\Psi v_{k_t}=\\lambda_{k_t} v_{k_t} \\tag{57} Ψvkt=λktvkt(57) 特征值满足: λkt=ejψkt=ej2πdλsin(θkt)(58) \\lambda_{k_t}=e\^{j\\psi_{k_t}}=e\^{j\\frac{2\\pi d}{\\lambda}\\sin(\\theta_{k_t})} \\tag{58} λkt=ejψkt=ejλ2πdsin(θkt)(58) 最终 DOA: θkt=arcsin(λ2πdarg(λkt))(59) \\theta_{k_t}=\\arcsin\\left(\\frac{\\lambda}{2\\pi d}\\arg(\\lambda_{k_t})\\right) \\tag{59} θkt=arcsin(2πdλarg(λkt))(59) ESPRIT 不需要像 MUSIC 那样在 θ\\thetaθ 上密集搜索伪谱,而是把 DOA 估计变成对一个 Kt×KtK_t\\times K_tKt×Kt 矩阵的特征值问题(当然前面仍要估计子空间)。这也是文章在摘要里强调 ESPRIT 更适合实时多目标场景的原因之一。 #### 7.6 Table 5:把"分辨率---鲁棒性---复杂度"三角关系写成可对比的工程表 **Table 5:Bartlett/MVDR/MUSIC/ESPRIT 对比** | Feature | Bartlett | MVDR | MUSIC | ESPRIT | |----------------------|-----------------------------------------------------------------------|--------------------------------------------------------------------------------------------------------|------------------------------------------------------------------------------------------------------------------|-----------------------------------------------------------------------------------------------------------------------------------------------| | Concept | Conventional beamforming scan | Adaptive beamforming, min interference/noise | Eigen-structure separates signal/noise subspace | Uses rotational invariance, avoids spectral search | | Mathematical basis | PB(θ)=aH(θ)Ra(θ)P_B(\\theta)=a\^H(\\theta)Ra(\\theta)PB(θ)=aH(θ)Ra(θ) | PMVDR(θ)=1/(aH(θ)R−1a(θ))P_{MVDR}(\\theta)=1/(a\^H(\\theta)R\^{-1}a(\\theta))PMVDR(θ)=1/(aH(θ)R−1a(θ)) | PMUSIC(θ)=1/(aH(θ)ENENHa(θ))P_{MUSIC}(\\theta)=1/(a\^H(\\theta)E_NE_N\^H a(\\theta))PMUSIC(θ)=1/(aH(θ)ENENHa(θ)) | R=ESΛSESH+ENΛNENHR=E_S\\Lambda_S E_S\^H + E_N\\Lambda_N E_N\^HR=ESΛSESH+ENΛNENH; Ψ=ES(1)†ES(2)\\Psi=E_S\^{(1)\\dagger}E_S\^{(2)}Ψ=ES(1)†ES(2) | | Complexity | O(M)O(M)O(M) | O(M3)O(M\^3)O(M3) | O(M3)O(M\^3)O(M3) | O(M2)O(M\^2)O(M2) | | Resolution | Poor (wide main lobe / high side lobe) | Moderate | High (super-resolution) | High (super-resolution, no search) | | Sensitivity to noise | High | Moderate | Low | Low | | Correlated sources | Poor | Moderate | Poor unless modified | Excellent | | Impact of velocity | High | Moderate (covariance errors sensitive) | High (snapshot decorrelation) | Lower than MUSIC (still affected by fast time-varying) | | Target scenarios | Single target | Closely placed | Multiple targets, high accuracy | Multiple targets, high accuracy | 当阵元数 MMM 增大时,O(M3)O(M\^3)O(M3) 的算法在硬件上会非常吃力,特别是车载雷达需要高刷新率(几十毫秒级甚至更快)时,高延迟会直接影响规划控制链路。随后作者提到 E-MUSIC 的思路:用"sketch"近似大协方差矩阵 R≈QBHQR\\approx QBHQR≈QBHQ 把复杂度降到 O(z2M)O(z\^2M)O(z2M),并声称在高 SNR 区域精度接近 MUSIC。在车载平台上,超分辨算法必须与低复杂度近似/结构化计算绑定,才有落地可能。 *** ** * ** *** ## 附录: ### A.1 从 (1)(2) 到 (3)(4):dechirp 后拍频 fB=kτf_B=k\\taufB=kτ 的完整推导(用三角恒等式看清"差频") 原文从发射 STx(t)S_{Tx}(t)STx(t) 与回波 SRx(t)S_{Rx}(t)SRx(t) 的余弦形式直接跳到了 IF 处只剩下一个 cos(2πfBt+θ)\\cos(2\\pi f_B t+\\theta)cos(2πfBt+θ)(式 (3)),中间省略的是"余弦相乘产生和频与差频,低通只保留差频"。 先取单目标(省略下标 iii),发射为 STx(t)=ATxcos(2πf0t+πkt2). S_{Tx}(t)=A_{Tx}\\cos\\big(2\\pi f_0 t+\\pi k t\^2\\big). STx(t)=ATxcos(2πf0t+πkt2). 回波为延迟衰减版本 SRx(t)=ATxαcos(2πf0(t−τ)+πk(t−τ)2). S_{Rx}(t)=A_{Tx}\\alpha\\cos\\big(2\\pi f_0(t-\\tau)+\\pi k (t-\\tau)\^2\\big). SRx(t)=ATxαcos(2πf0(t−τ)+πk(t−τ)2). 混频(相乘)得到 Smix(t)=STx(t)SRx(t)=ATx2αcosΦTx(t)cosΦRx(t), S_{mix}(t)=S_{Tx}(t)S_{Rx}(t) =A_{Tx}\^2\\alpha\\cos\\Phi_{Tx}(t)\\cos\\Phi_{Rx}(t), Smix(t)=STx(t)SRx(t)=ATx2αcosΦTx(t)cosΦRx(t), 其中 ΦTx(t)=2πf0t+πkt2,ΦRx(t)=2πf0(t−τ)+πk(t−τ)2. \\Phi_{Tx}(t)=2\\pi f_0 t+\\pi k t\^2,\\qquad \\Phi_{Rx}(t)=2\\pi f_0(t-\\tau)+\\pi k(t-\\tau)\^2. ΦTx(t)=2πf0t+πkt2,ΦRx(t)=2πf0(t−τ)+πk(t−τ)2. 用恒等式 cosacosb=12\[cos(a−b)+cos(a+b)\]\\cos a\\cos b=\\frac12\[\\cos(a-b)+\\cos(a+b)\]cosacosb=21\[cos(a−b)+cos(a+b)\],可得 Smix(t)=ATx2α2(cos(ΦTx(t)−ΦRx(t))+cos(ΦTx(t)+ΦRx(t))). S_{mix}(t)=\\frac{A_{Tx}\^2\\alpha}{2}\\Big(\\cos(\\Phi_{Tx}(t)-\\Phi_{Rx}(t))+\\cos(\\Phi_{Tx}(t)+\\Phi_{Rx}(t))\\Big). Smix(t)=2ATx2α(cos(ΦTx(t)−ΦRx(t))+cos(ΦTx(t)+ΦRx(t))). 其中 cos(ΦTx+ΦRx)\\cos(\\Phi_{Tx}+\\Phi_{Rx})cos(ΦTx+ΦRx) 是高频项(接近两倍载频与更高阶项),低通滤波 hL(t)h_L(t)hL(t) 会把它滤掉,只保留差相位项: SIF(t)≈ATx2α2cosΔΦ(t),ΔΦ(t)=ΦTx(t)−ΦRx(t). S_{IF}(t)\\approx \\frac{A_{Tx}\^2\\alpha}{2}\\cos\\Delta\\Phi(t),\\quad \\Delta\\Phi(t)=\\Phi_{Tx}(t)-\\Phi_{Rx}(t). SIF(t)≈2ATx2αcosΔΦ(t),ΔΦ(t)=ΦTx(t)−ΦRx(t). 现在把 ΔΦ(t)\\Delta\\Phi(t)ΔΦ(t) 展开。先展开回波相位的平方: (t−τ)2=t2−2tτ+τ2. (t-\\tau)\^2=t\^2-2t\\tau+\\tau\^2. (t−τ)2=t2−2tτ+τ2. 所以 ΦRx(t)=2πf0t−2πf0τ+πk(t2−2tτ+τ2). \\Phi_{Rx}(t)=2\\pi f_0 t-2\\pi f_0\\tau+\\pi k(t\^2-2t\\tau+\\tau\^2). ΦRx(t)=2πf0t−2πf0τ+πk(t2−2tτ+τ2). 于是相位差 ΔΦ(t)=(2πf0t+πkt2)−(2πf0t−2πf0τ+πkt2−2πktτ+πkτ2) \\Delta\\Phi(t) =\\big(2\\pi f_0 t+\\pi k t\^2\\big) -\\big(2\\pi f_0 t-2\\pi f_0\\tau+\\pi k t\^2-2\\pi k t\\tau+\\pi k\\tau\^2\\big) ΔΦ(t)=(2πf0t+πkt2)−(2πf0t−2πf0τ+πkt2−2πktτ+πkτ2) 化简得 ΔΦ(t)=2πf0τ+2πktτ−πkτ2. \\Delta\\Phi(t)=2\\pi f_0\\tau+2\\pi k t\\tau-\\pi k\\tau\^2. ΔΦ(t)=2πf0τ+2πktτ−πkτ2. 把它写成"线性相位 + 常数相位"的形式: ΔΦ(t)=2π(kτ)t+(2πf0τ−πkτ2)⏟θ (常数相位). \\Delta\\Phi(t)=2\\pi (k\\tau)t+\\underbrace{(2\\pi f_0\\tau-\\pi k\\tau\^2)}_{\\theta\\ \\text{(常数相位)}}. ΔΦ(t)=2π(kτ)t+θ (常数相位) (2πf0τ−πkτ2). 因此 SIF(t)≈ATx2α2cos(2π(kτ)t+θ). S_{IF}(t)\\approx \\frac{A_{Tx}\^2\\alpha}{2}\\cos\\big(2\\pi (k\\tau)t+\\theta\\big). SIF(t)≈2ATx2αcos(2π(kτ)t+θ). 对照式 (3),可识别 AIF=ATx2α2,fB=kτ,θ=2πf0τ−πkτ2, A_{IF}=\\frac{A_{Tx}\^2\\alpha}{2},\\qquad f_B=k\\tau,\\qquad \\theta=2\\pi f_0\\tau-\\pi k\\tau\^2, AIF=2ATx2α,fB=kτ,θ=2πf0τ−πkτ2, 而这正对应原文对 AIF,iA_{IF,i}AIF,i、θi\\theta_iθi 与 fB,if_{B,i}fB,i 的解释(PDF 第 7 页)。 再由往返时延 τ=2R/c\\tau=2R/cτ=2R/c,得到式 (4): fB=kτ=BTch⋅2Rc. f_B=k\\tau=\\frac{B}{T_{ch}}\\cdot \\frac{2R}{c}. fB=kτ=TchB⋅c2R. *** ** * ** *** ### A.2 从 (4)(7) 推出距离分辨率:为什么 ΔR=c2B\\Delta R=\\frac{c}{2B}ΔR=2Bc(把频率分辨率映射到距离) 由 (4) 有 fB=2kcR=2BcTchR. f_B=\\frac{2k}{c}R=\\frac{2B}{cT_{ch}}R. fB=c2kR=cTch2BR. 因此距离与拍频之间是线性映射: R=cTch2BfB. R=\\frac{cT_{ch}}{2B}f_B. R=2BcTchfB. 如果我们对一个 chirp 的 IF 信号在快时间上做 FFT,其频率分辨率近似为 ΔfB≈1Tobs, \\Delta f_B\\approx \\frac{1}{T_{obs}}, ΔfB≈Tobs1, 其中 TobsT_{obs}Tobs 是有效观测时长。理想情况下 TobsT_{obs}Tobs 与 TchT_{ch}Tch 同量级(实际可能因采样窗口、调制、窗函数略有差异,但不影响比例结论)。于是拍频的最小可分辨差对应的距离差为 ΔR=cTch2BΔfB≈cTch2B⋅1Tch=c2B. \\Delta R=\\frac{cT_{ch}}{2B}\\Delta f_B \\approx \\frac{cT_{ch}}{2B}\\cdot\\frac{1}{T_{ch}} =\\frac{c}{2B}. ΔR=2BcTchΔfB≈2BcTch⋅Tch1=2Bc. 这就回到了原文式 (7)。这段推导想强调的是:ΔR\\Delta RΔR 与带宽的倒数成正比,本质上来自傅里叶变换的"时间-频率不确定性";而系数 1/21/21/2 来自往返传播导致的 2R/c2R/c2R/c。 *** ** * ** *** ### A.3 从 (9)(10) 推出速度估计:Δθ=2πfDTch\\Delta\\theta=2\\pi f_D T_{ch}Δθ=2πfDTch 与 v=λΔθ/(4πTch)v=\\lambda\\Delta\\theta/(4\\pi T_{ch})v=λΔθ/(4πTch) 原文给出速度估计式 (10),但没写中间相位关系。把 Doppler 看成慢时间上的复指数更清楚:对固定距离 bin,假设其跨 chirp 的复幅度(忽略噪声)可以写为 z\[r\]∝ej2πfDrTch. z\[r\]\\propto e\^{j2\\pi f_D rT_{ch}}. z\[r\]∝ej2πfDrTch. 那么相邻 chirp 的相位差是 Δθ=arg(z\[r+1\])−arg(z\[r\])=2πfDTch. \\Delta\\theta=\\arg(z\[r+1\])-\\arg(z\[r\])=2\\pi f_D T_{ch}. Δθ=arg(z\[r+1\])−arg(z\[r\])=2πfDTch. 又 fD=2vλf_D=\\frac{2v}{\\lambda}fD=λ2v,代入得到 Δθ=2π2vλTch⇒v=λ4πTchΔθ, \\Delta\\theta=2\\pi\\frac{2v}{\\lambda}T_{ch} \\quad\\Rightarrow\\quad v=\\frac{\\lambda}{4\\pi T_{ch}}\\Delta\\theta, Δθ=2πλ2vTch⇒v=4πTchλΔθ, 正是式 (10) 的来源。 进一步地,式 (12) 的速度分辨率也可以从慢时间 FFT 的频率分辨率得到:若一帧的慢时间观测时长为 TfT_fTf,则 ΔfD≈1/Tf\\Delta f_D\\approx 1/T_fΔfD≈1/Tf。又 v=λ2fDv=\\frac{\\lambda}{2}f_Dv=2λfD,于是 Δv=λ2ΔfD≈λ2Tf, \\Delta v=\\frac{\\lambda}{2}\\Delta f_D\\approx\\frac{\\lambda}{2T_f}, Δv=2λΔfD≈2Tfλ, 即式 (12)。 *** ** * ** *** ### A.4 从 (25)(26) 到 (27):4D-FFT 的"离散化与物理参数映射" 原文在 (25)(26) 后说"Thus, ... implementation of 4D FFT is required",并给出 (27),但没把每个指数项如何对应 FFT 核写出来。这里把逻辑补齐。 把 dechirp 后信号(简化为单目标、忽略常数相位)写成典型形式: x\~m,r(t)≈A\~ ej2πfBt ej2πfDrTc ejφsp(m)+v\~m,r(t), \\tilde x_{m,r}(t)\\approx \\tilde A\\,e\^{j2\\pi f_B t}\\,e\^{j2\\pi f_D rT_c}\\,e\^{j\\varphi_{sp}(m)}+\\tilde v_{m,r}(t), x\~m,r(t)≈A\~ej2πfBtej2πfDrTcejφsp(m)+v\~m,r(t), 其中 fBf_BfB 是拍频,fDf_DfD 是 Doppler,φsp(m)\\varphi_{sp}(m)φsp(m) 是阵列空间相位(由入射角决定)。 对快时间采样 t=lTst=lT_st=lTs,得 x\[l,r,m\]=x\~m,r(lTs)≈A\~ ej2πfBlTs ej2πfDrTc ejφsp(m)+noise. x\[l,r,m\]=\\tilde x_{m,r}(lT_s)\\approx \\tilde A\\,e\^{j2\\pi f_B lT_s}\\,e\^{j2\\pi f_D rT_c}\\,e\^{j\\varphi_{sp}(m)}+\\text{noise}. x\[l,r,m\]=x\~m,r(lTs)≈A\~ej2πfBlTsej2πfDrTcejφsp(m)+noise. 如果做快时间 DFT(长度 LLL): X\[p,r,m\]=∑l=0L−1x\[l,r,m\]e−j2πpLl. X\[p,r,m\]=\\sum_{l=0}\^{L-1}x\[l,r,m\]e\^{-j2\\pi \\frac{p}{L}l}. X\[p,r,m\]=l=0∑L−1x\[l,r,m\]e−j2πLpl. 当 pL\\frac{p}{L}Lp 与 fBTsf_B T_sfBTs 对齐时,求和项同相叠加,出现峰值,这就是距离 bin;因此 ppp 对应拍频,进而通过 (4)(5) 映射到距离 RRR。 接着对慢时间(长度 RRR 个 chirp)做 DFT: X\[p,q,m\]=∑r=0R−1X\[p,r,m\]e−j2πqRr. X\[p,q,m\]=\\sum_{r=0}\^{R-1}X\[p,r,m\]e\^{-j2\\pi \\frac{q}{R}r}. X\[p,q,m\]=r=0∑R−1X\[p,r,m\]e−j2πRqr. 当 qR\\frac{q}{R}Rq 与 fDTcf_D T_cfDTc 对齐时得到 Doppler 峰,qqq 对应速度 bin。 最后对空间维做波束扫描/空间 FFT。以 UPA(水平 mhm_hmh、垂直 mvm_vmv)为例,空间相位可写成 ##
\varphi_{sp}(m_h,m_v)
2\pi\frac{d_a}{\lambda}
\left(m_h\sin\theta\cos\phi+m_v\sin\phi\right),
于是空间 DFT/扫描核正是 (27) 后两项: ej2πdaλmhsinθcosϕ ej2πdaλmvsinϕ. e\^{j2\\pi\\frac{d_a}{\\lambda} m_h\\sin\\theta\\cos\\phi}\\, e\^{j2\\pi\\frac{d_a}{\\lambda} m_v\\sin\\phi}. ej2πλdamhsinθcosϕej2πλdamvsinϕ. 把三步合起来,就是式 (27) 的 4D 求和结构。 *** ** * ** *** ### A.5 作者只写了 (28) 的不等式:CA-CFAR 的 KCFARK_{CFAR}KCFAR 如何由虚警概率推导出来 Fig. 8 画出了 KCFARK_{CFAR}KCFAR 与 ZCFARZ_{CFAR}ZCFAR,但没给 KCFARK_{CFAR}KCFAR 与虚警概率 PFAP_{FA}PFA 的解析关系。这里给出经典 CA-CFAR 推导(假设噪声为复高斯,功率服从指数分布;训练单元独立同分布)。 设 CUT 的噪声功率为随机变量 XXX,训练单元功率为 X1,...,XNX_1,\\ldots,X_NX1,...,XN,它们在无目标假设 H0H_0H0 下独立同分布,且 X∼Exponential(σ2),Xi∼Exponential(σ2). X\\sim \\text{Exponential}(\\sigma\^2),\\qquad X_i\\sim \\text{Exponential}(\\sigma\^2). X∼Exponential(σ2),Xi∼Exponential(σ2). CA-CFAR 用训练单元均值作为噪声估计: Z=1N∑i=1NXi. Z=\\frac{1}{N}\\sum_{i=1}\^N X_i. Z=N1i=1∑NXi. 阈值设为 T=KZ. T=K Z. T=KZ. 虚警概率定义为在 H0H_0H0 下误报目标的概率: PFA=Pr(X\>T)=Pr(X\>KZ). P_{FA}=\\Pr(X\>T)=\\Pr(X\>KZ). PFA=Pr(X\>T)=Pr(X\>KZ). 条件于 Z=zZ=zZ=z 时, Pr(X\>Kz∣Z=z)=exp(−Kzσ2), \\Pr(X\>Kz\\mid Z=z)=\\exp\\left(-\\frac{Kz}{\\sigma\^2}\\right), Pr(X\>Kz∣Z=z)=exp(−σ2Kz), 因为指数分布尾概率为 Pr(X\>x)=e−x/σ2\\Pr(X\>x)=e\^{-x/\\sigma\^2}Pr(X\>x)=e−x/σ2。因此 PFA=EZ\[exp(−KZσ2)\]. P_{FA}=\\mathbb E_Z\\left\[\\exp\\left(-\\frac{KZ}{\\sigma\^2}\\right)\\right\]. PFA=EZ\[exp(−σ2KZ)\]. 而 ∑i=1NXi\\sum_{i=1}\^N X_i∑i=1NXi 是 NNN 个指数分布之和,服从 Gamma 分布;等价地,ZZZ 的拉普拉斯变换为 E\[e−sZ\]=(11+sσ2/N)N. \\mathbb E\\left\[e\^{-sZ}\\right\]=\\left(\\frac{1}{1+s\\sigma\^2/N}\\right)\^N. E\[e−sZ\]=(1+sσ2/N1)N. 令 s=K/σ2s=K/\\sigma\^2s=K/σ2,得到 PFA=(11+K/N)N. P_{FA}=\\left(\\frac{1}{1+K/N}\\right)\^N. PFA=(1+K/N1)N. 解出 KKK: PFA−1/N=1+KN⇒K=N(PFA−1/N−1). P_{FA}\^{-1/N}=1+\\frac{K}{N} \\quad\\Rightarrow\\quad K=N\\left(P_{FA}\^{-1/N}-1\\right). PFA−1/N=1+NK⇒K=N(PFA−1/N−1). 这就是工程上常用的 CA-CFAR 阈值系数。它把 Fig. 8 中"KCFARK_{CFAR}KCFAR"变成了一个可直接算的设计量:给定训练单元数 NNN 与期望虚警率 PFAP_{FA}PFA,阈值倍数 KKK 就确定了。原文虽然没写,但它与 (28) 与 Fig. 8 的结构完全一致。 *** ** * ** *** ### A.6 从 (34) 到 (35):MVDR 权值的拉格朗日推导 式 (34) 是约束二次型最小化: minwwHRw,s.t. wHa=1. \\min_w w\^H R w,\\quad \\text{s.t. } w\^H a=1. wminwHRw,s.t. wHa=1. 构造拉格朗日函数(复数情形常写成带共轭乘子): L(w,μ)=wHRw+μ(1−wHa)+μ∗(1−aHw). \\mathcal L(w,\\mu)=w\^H R w+\\mu(1-w\^H a)+\\mu\^\*(1-a\^H w). L(w,μ)=wHRw+μ(1−wHa)+μ∗(1−aHw). 对 w∗w\^\*w∗ 求导并令其为 0(用复矩阵微分结论 ∂(wHRw)/∂w∗=Rw\\partial(w\^HRw)/\\partial w\^\*=Rw∂(wHRw)/∂w∗=Rw): ∂L∂w∗=Rw−μa=0⇒w=μR−1a. \\frac{\\partial \\mathcal L}{\\partial w\^\*}=Rw-\\mu a=0 \\quad\\Rightarrow\\quad w=\\mu R\^{-1}a. ∂w∗∂L=Rw−μa=0⇒w=μR−1a. 代入约束 wHa=1w\^Ha=1wHa=1: (μR−1a)Ha=μ∗aHR−Ha=μ∗aHR−1a=1. (\\mu R\^{-1}a)\^H a=\\mu\^\* a\^H R\^{-H}a=\\mu\^\* a\^H R\^{-1}a=1. (μR−1a)Ha=μ∗aHR−Ha=μ∗aHR−1a=1. 因此 μ=1aHR−1a. \\mu=\\frac{1}{a\^H R\^{-1}a}. μ=aHR−1a1. 最终得到 wMVDR=R−1aaHR−1a, w_{MVDR}=\\frac{R\^{-1}a}{a\^H R\^{-1}a}, wMVDR=aHR−1aR−1a, 即式 (35)。而把该权值代回输出功率 P(w)=wHRwP(w)=w\^HRwP(w)=wHRw 可得到 PMVDR(θ)=1aH(θ)R−1a(θ), P_{MVDR}(\\theta)=\\frac{1}{a\^H(\\theta)R\^{-1}a(\\theta)}, PMVDR(θ)=aH(θ)R−1a(θ)1, 即式 (36)。 *** ** * ** *** ### A.7 从 (37) 到 (44):MUSIC 伪谱为什么等价于"最小化噪声子空间投影"并产生峰值 原文给出 R=ARsAH+σ2I. R=A R_s A\^H+\\sigma\^2 I. R=ARsAH+σ2I. 若目标数为 KtK_tKt,则信号子空间由 AAA 的列空间张成。对理想情况(源不相关、噪声白、快拍充分),RRR 的前 KtK_tKt 个特征向量张成与 AAA 相同的子空间,剩余 M−KtM-K_tM−Kt 个特征向量张成噪声子空间 UnU_nUn。因此对任意真实 DOA θk\\theta_kθk,其导向矢量 a(θk)a(\\theta_k)a(θk) 属于信号子空间,必与噪声子空间正交: UnHa(θk)=0. U_n\^H a(\\theta_k)=0. UnHa(θk)=0. 于是噪声子空间投影范数 ∥UnHa(θ)∥22=aH(θ)UnUnHa(θ) \\\|U_n\^H a(\\theta)\\\|_2\^2 = a\^H(\\theta)U_nU_n\^H a(\\theta) ∥UnHa(θ)∥22=aH(θ)UnUnHa(θ) 在 θ=θk\\theta=\\theta_kθ=θk 处趋近 0。MUSIC 通过取倒数把"接近 0"转成"巨大峰值": PMUSIC(θ)=1aH(θ)UnUnHa(θ). P_{MUSIC}(\\theta)=\\frac{1}{a\^H(\\theta)U_nU_n\^H a(\\theta)}. PMUSIC(θ)=aH(θ)UnUnHa(θ)1. 所以 MUSIC 的"超分辨峰"本质上来自一个几何事实:真实导向矢量落在信号子空间里,与噪声子空间正交;而伪谱只是把这个正交性变成可搜索的峰。 *** ** * ** *** ### A.8 ESPRIT 的关键一跳:为何 U2=U1ΨU_2=U_1\\PsiU2=U1Ψ 成立、以及 Ψ\\PsiΨ 的特征值为何携带 sinθ\\sin\\thetasinθ 原文在 (55) 写 U2=U1ΨU_2=U_1\\PsiU2=U1Ψ,但省略了"子空间与阵列流形同构"的解释。把它补齐如下: 由于 x(t)=As(t)+n(t), x(t)=A s(t)+n(t), x(t)=As(t)+n(t), 信号子空间由 AAA 的列空间张成。样本协方差 EVD 得到的 UsU_sUs 也张成同一信号子空间,因此存在一个可逆矩阵 TTT 使得 Us=AT. U_s=A T. Us=AT. 对子阵选择矩阵 Je1,Je2J_{e1},J_{e2}Je1,Je2 作用: U1=Je1Us=Je1AT=A1T, U_1=J_{e1}U_s=J_{e1}A T=A_1 T, U1=Je1Us=Je1AT=A1T, U2=Je2Us=Je2AT=A2T. U_2=J_{e2}U_s=J_{e2}A T=A_2 T. U2=Je2Us=Je2AT=A2T. 而平移不变性给出 A2=A1ΦA_2=A_1\\PhiA2=A1Φ,因此 U2=A2T=A1ΦT. U_2=A_2 T=A_1\\Phi T. U2=A2T=A1ΦT. 又 U1=A1TU_1=A_1 TU1=A1T,两式相消得到 U2=U1(T−1ΦT). U_2=U_1 (T\^{-1}\\Phi T). U2=U1(T−1ΦT). 令 Ψ=T−1ΦT, \\Psi=T\^{-1}\\Phi T, Ψ=T−1ΦT, 即可得到式 (55) 的形式 U2=U1ΨU_2=U_1\\PsiU2=U1Ψ。这解释了为什么 Ψ\\PsiΨ 与 Φ\\PhiΦ 相似(similar),从而拥有相同的特征值。由于 Φ=diag(ejψ1,...,ejψK), \\Phi=\\mathrm{diag}(e\^{j\\psi_1},\\ldots,e\^{j\\psi_K}), Φ=diag(ejψ1,...,ejψK), Ψ\\PsiΨ 的特征值就是 ejψke\^{j\\psi_k}ejψk。对 ULA 平移一个阵元距离 ddd 的相位旋转满足 ψk=2πdλsinθk, \\psi_k=\\frac{2\\pi d}{\\lambda}\\sin\\theta_k, ψk=λ2πdsinθk, 于是 λk=ejψk=ej2πdλsinθk, \\lambda_k=e\^{j\\psi_k}=e\^{j\\frac{2\\pi d}{\\lambda}\\sin\\theta_k}, λk=ejψk=ejλ2πdsinθk, 这就是式 (58)。最后用特征值辐角恢复 θk\\theta_kθk,得到式 (59)。 *** ** * ** *** ### A.9 从 (22) 到 (23)(24):KFMCW=ΔFRF/ΔFBbK_{FMCW}=\\Delta F_{RF}/\\Delta F_{Bb}KFMCW=ΔFRF/ΔFBb 为什么会变成"斜率差的倒数" 原文先定义 KFMCW=ΔFRFIΔFBbI. K_{FMCW}=\\frac{\\Delta F_{RF}\^I}{\\Delta F_{Bb}\^I}. KFMCW=ΔFBbIΔFRFI. 关键在于:FMCW-FMCW 干扰在受害雷达下变频后表现为"一个扫过接收带通的 chirp",它在基带占用的带宽 ΔFBbI\\Delta F_{Bb}\^IΔFBbI 由两条 chirp 的相对扫频率决定。设受害雷达扫频斜率为 SwVS_w\^VSwV,干扰雷达为 SwIS_w\^ISwI。两者瞬时频率之差随时间变化的斜率近似是 ddtΔf(t)=SwV−SwI. \\frac{d}{dt}\\Delta f(t)=S_w\^V-S_w\^I. dtdΔf(t)=SwV−SwI. 当干扰扫过受害雷达通带(设通带宽度与干扰 RF 扫频宽度同阶为 ΔFRFI\\Delta F_{RF}\^IΔFRFI)时,扫过所需时间与斜率差成反比: Tcross≈ΔFRFI∣SwV−SwI∣. T_{\\text{cross}}\\approx \\frac{\\Delta F_{RF}\^I}{\|S_w\^V-S_w\^I\|}. Tcross≈∣SwV−SwI∣ΔFRFI. 而在这段时间内,经过下变频与滤波,等效基带带宽与"扫过速度"有关,可理解为被映射到一个与 ∣SwV−SwI∣\|S_w\^V-S_w\^I\|∣SwV−SwI∣ 相关的 ΔFBbI\\Delta F_{Bb}\^IΔFBbI。当两者起始频率/时间对齐(Type A),给出的结果等价于 ΔFBbI∝∣SwV−SwI∣ Ts,ΔFRFI∝∣SwI∣ Ts, \\Delta F_{Bb}\^I \\propto \|S_w\^V-S_w\^I\|\\,T_s, \\quad \\Delta F_{RF}\^I \\propto \|S_w\^I\|\\,T_s, ΔFBbI∝∣SwV−SwI∣Ts,ΔFRFI∝∣SwI∣Ts, 从而 KFMCW=ΔFRFIΔFBbI≈∣SwISwV−SwI∣, K_{FMCW} =\\frac{\\Delta F_{RF}\^I}{\\Delta F_{Bb}\^I} \\approx \\left\|\\frac{S_w\^I}{S_w\^V-S_w\^I}\\right\|, KFMCW=ΔFBbIΔFRFI≈ SwV−SwISwI , 对应式 (23)。Type B 多出的系数 2(式 (24))可理解为中心频率对齐导致干扰扫过通带的对称/双侧效应(原文直接给出 2 倍系数)。两雷达扫频斜率越接近,差频扫过越慢,干扰在受害雷达基带停留越久、能量越集中,于是 KFMCWK_{FMCW}KFMCW 越大,互扰越严重。