1.带环链表问题
1.1给定一个链表判断其是否带环
解决思路:利用快慢指针法,快指针一次走两步慢指针一次走一步,从链表起始位置遍历链表,如果链表带环,则快慢指针一定会在环中相遇,否则快指针先到达链表末尾。
代码实现:(链表的实现请跳转☞http://t.csdnimg.cn/JeNAV)
cpp
SLNode* IsLink(SLNode* head)
{
SLNode* fast = head;
SLNode* slow = head;
//让快慢指针先走一步进循环
fast = fast->next->next;
slow = slow->next;
//这里是循环的条件:快慢指针未相遇、快指针未到链表末端
while ((fast != slow) && (fast != NULL))
{
fast = fast->next->next;
slow = slow->next;
}
if (fast == slow)
{
return fast;
}
if(fast==NULL)
{
return NULL;
}
}
void test()
{
//创建一个带环链表
SLNode* Node1 = SLBuyNode(1);
SLNode* Node2 = SLBuyNode(2);
SLNode* Node3 = SLBuyNode(3);
SLNode* Node4 = SLBuyNode(4);
SLNode* Node5 = SLBuyNode(5);
SLNode* Node6 = SLBuyNode(6);
SLNode* Node7 = SLBuyNode(7);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Node4->next = Node5;
Node5->next = Node6;
Node6->next = Node7;
Node7->next = Node4;
//判断是否带环,如果带环打印相遇节点,如果不带环打印"NULL"
if (IsLink(Node1) == NULL)
{
printf("NULL\n");
}
else
{
printf("%d\n", IsLink(Node1)->Data);
}
}
int main()
{
test();
return 0;
}1.2给定一个带环链表,返回链表开始入环的第一个节点
解决方案:让一个指针从链表头开始遍历链表,同时另一个指针从判断相遇位置开始绕环运行,两个指针都是一次走一步,最终会在进环的第一个节点相遇。
证明:
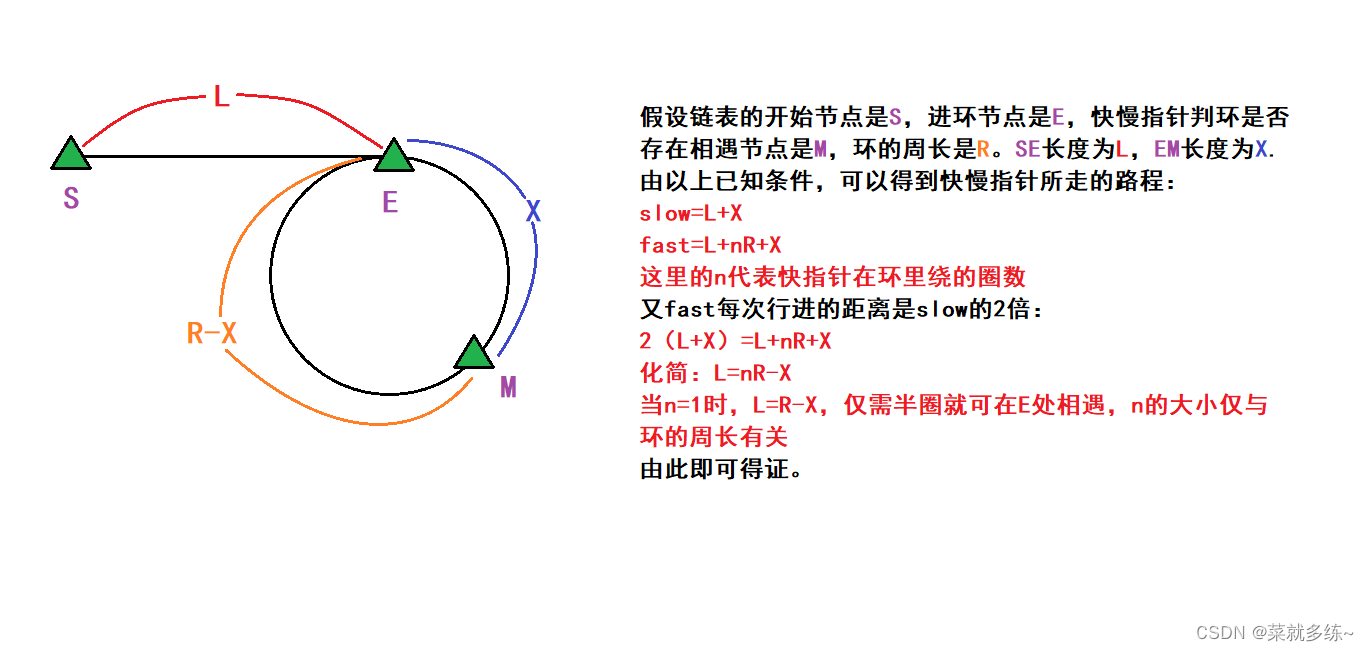
代码实现:
cpp
//判断是否为带环链表
SLNode* IsLink(SLNode* head)
{
SLNode* fast = head;
SLNode* slow = head;
//让快慢指针先走一步进循环
fast = fast->next->next;
slow = slow->next;
//这里是循环的条件:快慢指针未相遇、快指针未到链表末端
while ((fast != slow) && (fast != NULL))
{
fast = fast->next->next;
slow = slow->next;
}
if (fast == slow)
{
return fast;
}
if(fast==NULL)
{
return NULL;
}
}
//返回带环链表的进环节点
SLNode* EntryNode(SLNode* head, SLNode* M)
{
SLNode* a = head;
SLNode* b = M;
while (a != b)
{
a = a->next;
b = b->next;
}
return a;
}
void test2()
{
//创建一个带环链表:1->2->3->4->5->6->7->4->5...
SLNode* Node1 = SLBuyNode(1);
SLNode* Node2 = SLBuyNode(2);
SLNode* Node3 = SLBuyNode(3);
SLNode* Node4 = SLBuyNode(4);
SLNode* Node5 = SLBuyNode(5);
SLNode* Node6 = SLBuyNode(6);
SLNode* Node7 = SLBuyNode(7);
Node1->next = Node2;
Node2->next = Node3;
Node3->next = Node4;
Node4->next = Node5;
Node5->next = Node6;
Node6->next = Node7;
Node7->next = Node4;
//返回进环节点
SLNode* M = IsLink(Node1);
SLNode* E = EntryNode(Node1, M);
printf("%d\n", E->Data);
}
int main()
{
test2();
return 0;
}2.循环队列问题
2.1循环队列
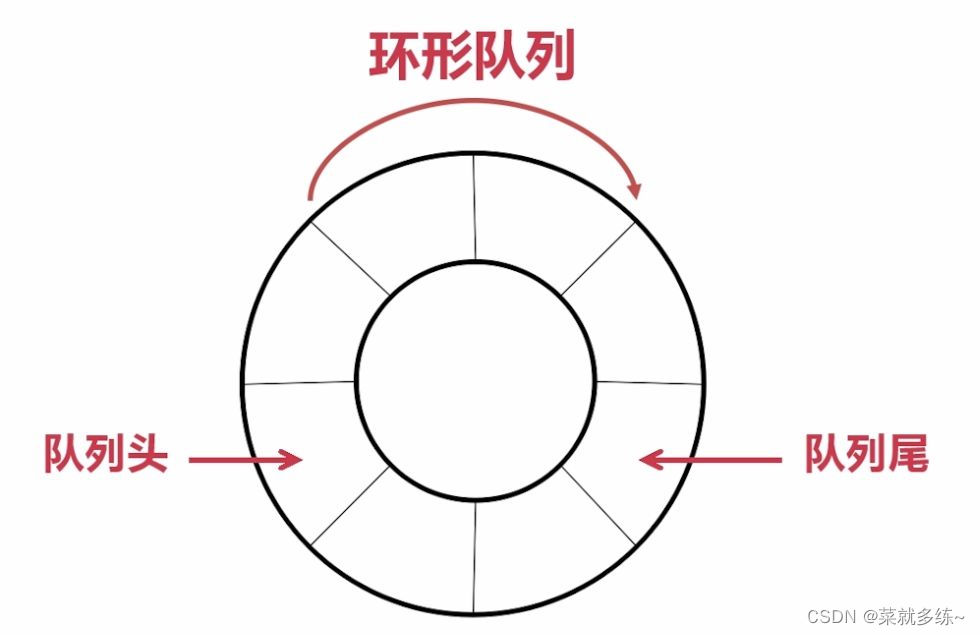
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
2.2代码实现:
CircularQueue.h
cpp
#include<stdlib.h>
#include<stdio.h>
#include<assert.h>
#include<stdbool.h>
#include<math.h>
typedef int CQDataType;
typedef struct CircularQueue
{
CQDataType* a; //利用数组实现循环链表
int head; //指向头
int tail; //指向尾的下一个
}CQueue;
//初始化
void CQInit(CQueue* q);
//入队列
void CQPush(CQueue* q, CQDataType x);
//出队列
void CQPop(CQueue* q);
//查看队头
CQDataType CQTop(CQueue* q);
//数据有效个数
size_t CQSize(CQueue* q);
//判空
bool CQEmpty(CQueue* q);
//判满
bool CQFull(CQueue* q);
//销毁
void CQDestroy(CQueue* q);CircularQueue.c
cpp
#include"CircularQueue.h"
//初始化
void CQInit(CQueue* q)
{
assert(q);
//创建一个5+1的数组实现容量为5的循环队列
q->a = (CQDataType*)malloc(sizeof(CQDataType)*6);
q->head = q->tail = 0;
}
//判满
bool CQFull(CQueue* q)
{
assert(q);
return (q->tail + 1) % 6 == q->head;
}
//入队列(入队列前需判断是否满)
void CQPush(CQueue* q, CQDataType x)
{
assert(q);
//判满
if (CQFull(q))
{
perror("CQFull(q) is full");
return;
}
//第一个数据入队列
if (q->head == q->tail == 0)
{
q->a[q->tail] = x;
q->tail++;
}
else
{
q->a[q->tail] = x;
q->tail++;
}
q->tail = q->tail % 6;
}
//判空
bool CQEmpty(CQueue* q)
{
assert(q);
return q->head == q->tail;
}
//出队列(出队列前判空)
void CQPop(CQueue* q)
{
assert(q);
if (CQEmpty(q))
{
perror("CQEmpty(q) is true");
return;
}
q->head++;
q->head = q->head % 6;
}
//查看队头
CQDataType CQTop(CQueue* q)
{
assert(q);
assert(CQEmpty(q) != true);
return q->a[q->head];
}
//数据有效个数
size_t CQSize(CQueue* q)
{
assert(q);
if (q->tail < q->head)
{
return 6 - q->head + q->tail - 0;
}
return abs(q->tail - q->head);
}
//销毁
void CQDestroy(CQueue* q)
{
assert(q);
free(q->a);
q->a = NULL;
q->head = q->tail = 0;
}以上便是本期讨论的两个数据结构问题,欢迎大家评论讨论交流。