目录
考察单链表操作的综合应用能力;找中点(快慢指针法)和链表反转的实现
考察在特定约束下(空间可重用、动态扩展)选择合适数据结构的能力,强调链式存储的优势(避免顺序存储的扩容开销);队空/队满;入队/出队;循环链表
考察程序段时间复杂度
给定程序段,判断其时间复杂度
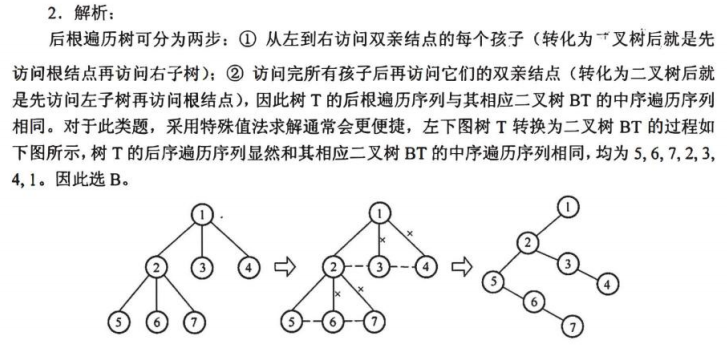
考察树与二叉树的转换关系,不同遍历方式
判断树转二叉树后,哪种遍历序列与树后根遍历相同
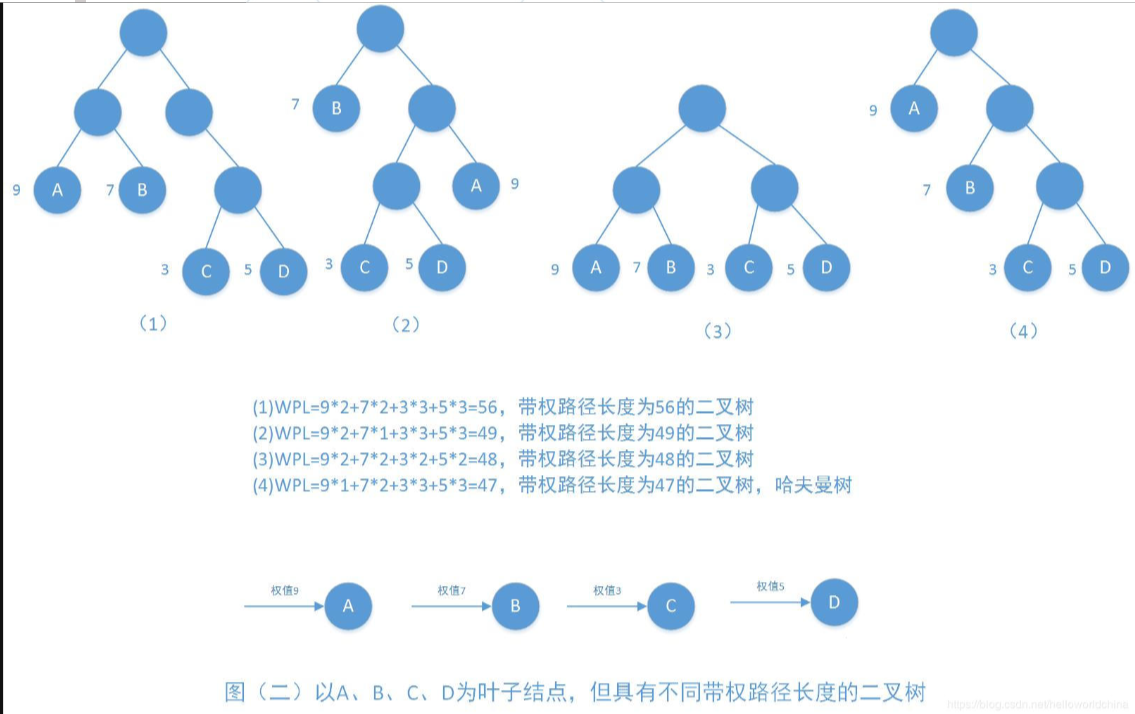
考察哈夫曼树的构造原理和性质
已知哈夫曼树结点数,求符号个数n
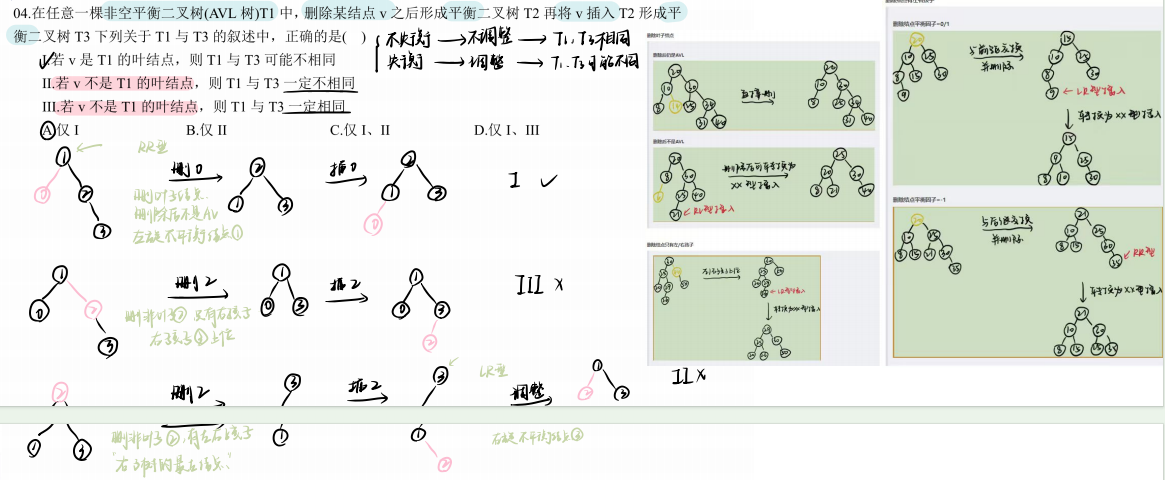
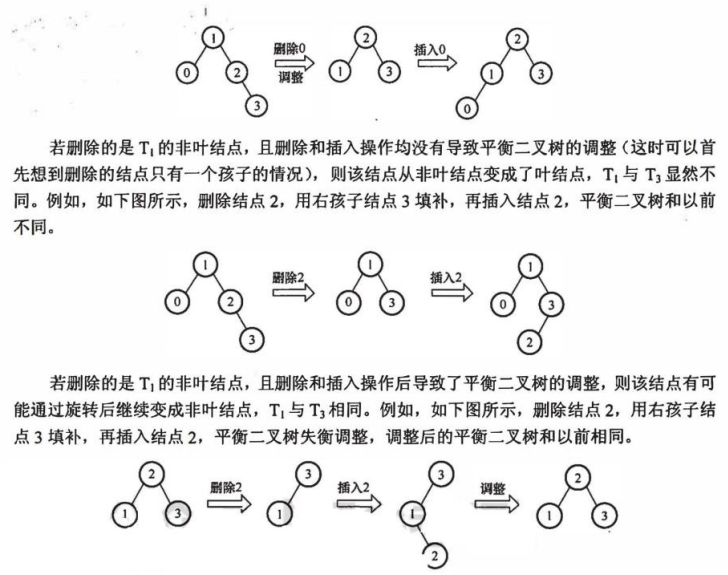
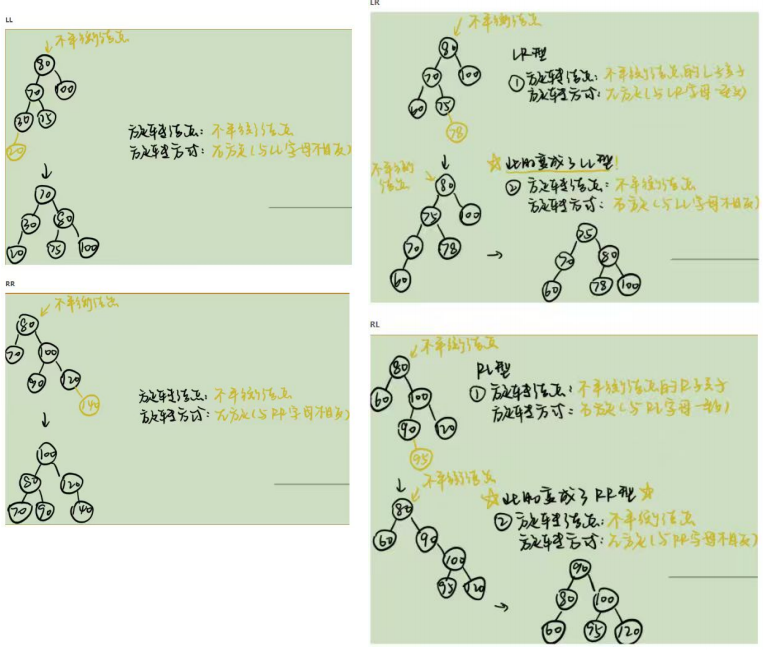
考察平衡二叉树的性质和操作(删除、插入)
分析AVL树删除并插入结点后与袁树的关系
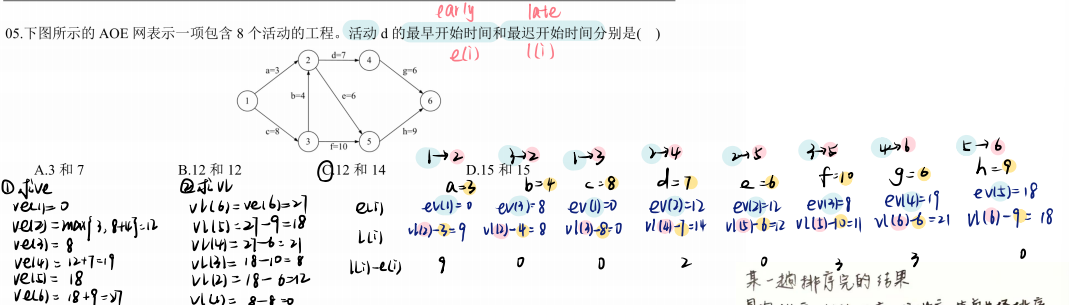
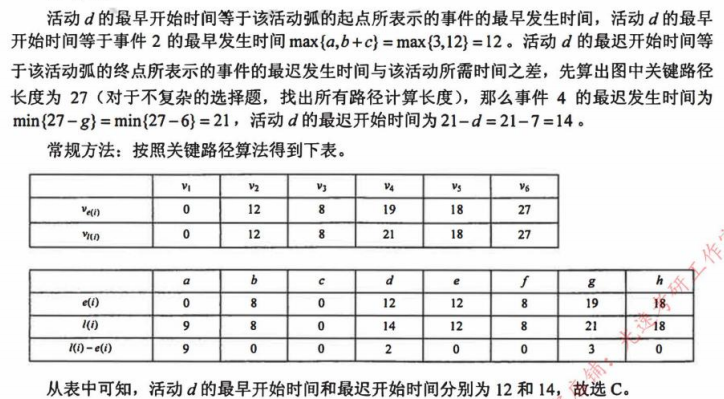
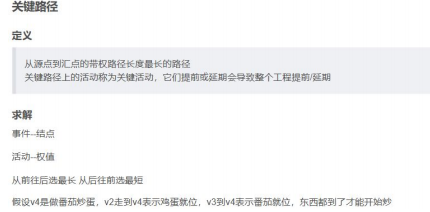
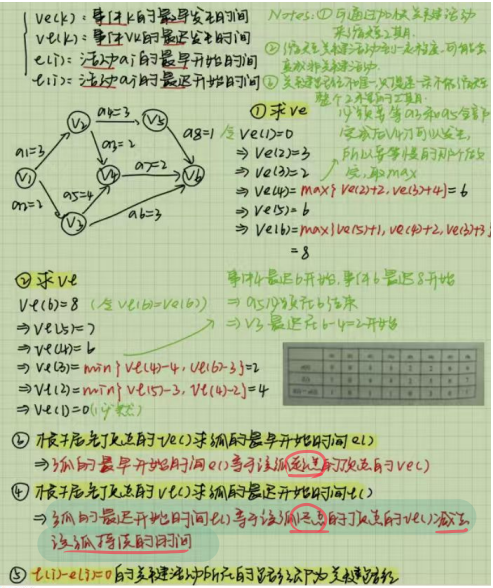
考察AOE网;计算活动时间;关键路径
求AOE网中活动d的最早和最迟开始时间
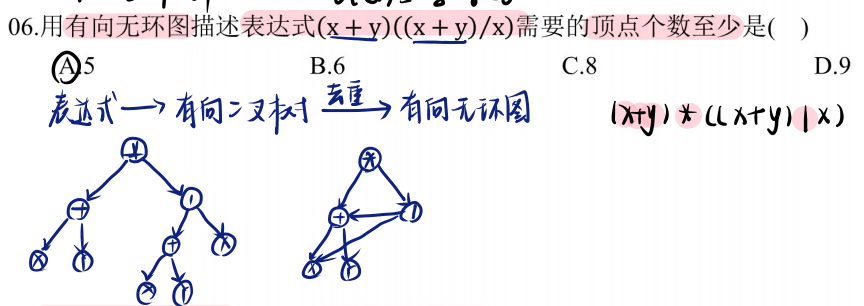
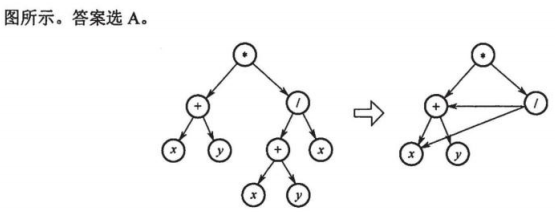
考察表达式--->图
用有向无环图描述表达式,求顶点个数
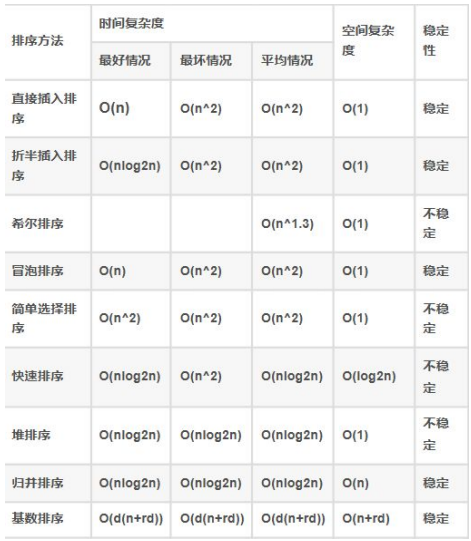
考察对排序算法综合理解
判断选择排序算法时需要考虑的因素
考察散列表概念;散列函数;冲突解决方法
给定散列表相关信息,求查找失败平均查找长度
"7"--映射到的地址树数
H(key)=key%7;线性探查法;87(3)、40(5)、30(2)、6(6)、11(4)、22(1)、98(0)、20(6-->7)
查找失败(比较完0~8号地址后才能确定该关键字不在表中)
0:探测0-->1-->2-->3-->4-->5-->6-->7-->8(9次)
1:探测1-->2-->3-->4-->5-->6-->7-->8(8次)
2:探测2-->3-->4-->5-->6-->7-->8(7次)
3:探测3-->4-->5-->6-->7-->8(6次)
4:探测4-->5-->6-->7-->8(5次)
5:探测5-->6-->7-->8(4次)
6:探测6-->7-->8(3次)
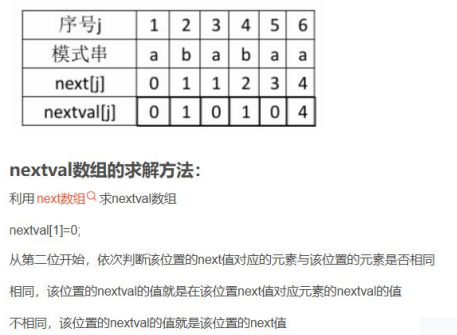
考察KMP算法;字符匹配
用KMP算法对给定字符串匹配,求字符比较次数
考察快速排序的过程;分析排序结果
判断那个序列不可能是快速排序第二趟结果
考察外部排序;最佳归并树构造
给定初始归并段数和归并路数,求补充虚段个数
考察单链表操作的综合应用能力;找中点(快慢指针法)和链表反转的实现
单链表基本操作:遍历、找中点、链表反转、合并链表
空间优化策略:不使用额外数据结构,仅通过指针操作完成重排
算法效率分析:实践复杂度需结合链表长度n,考虑线性时间内完成操作
设计空间高效的算法:避免使用栈或额外链表存储元素,指针操作
链表重排逻辑;如何将反转后的后半部分与前半部分交替合并
单链表对称重排算法设计
给定带头结点的单链表L=(a1,a2,...,an),要求设计算法将其重排为L'=(a1,an,a2,an-1,...),要求空间复杂度O(1)
核心设计思想:
采用"三步走"策略,在O(1)空间内完成重排;
第一步:找链表中点:使用快慢指针(慢指针一次走1步,快指针一次走2步),当快指针达到尾部时,慢指针指向链表的下中位数(左半段最后一个节点),将链表分为左半段(L1:a1-->a2-->...ak)和右半段(L2:ak-1-->...an)
第二步:反转右半段:将右半段L2反转(变为an-->...ak-1),便于后续交叉合并
第三步:交叉合并,将左半段L1和反转后的右半段L2交叉拼接(a1-->an-->an-1-->...),形成目标链表
考察在特定约束下(空间可重用、动态扩展)选择合适数据结构的能力,强调链式存储的优势(避免顺序存储的扩容开销);队空/队满;入队/出队;循环链表
队空条件(头尾指针相同,且指向空)、队满条件(通常无显式队满,可动态申请结点)
队列操作,如入队时从空闲池取节点或新建,出队时将节点放回空闲池
队列存储结构选择:链式存储(动态分配结点)vs顺序存储(静态数组)
动态内存管理:出队节点不释放,而是加入空间节点池,实现空间重复利用
队列操作原子性:入队和出队需保证O(1)时间,通过维护头尾指针实现
动态可重用队列设计
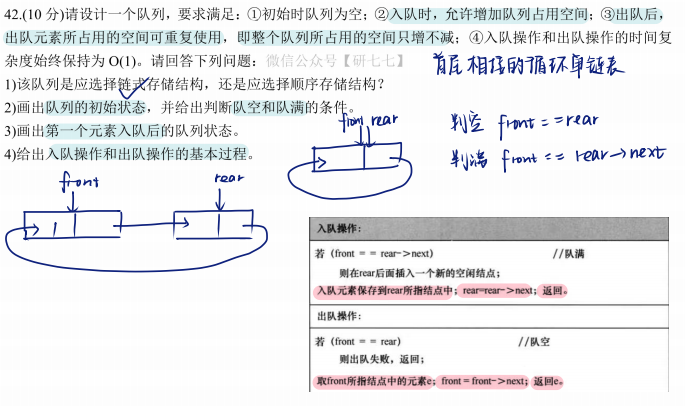
设计队列满足:初始为空,入队可扩展空间,出队元素可重复使用,操作时间复杂度O(1),需选择存储结构,定义队空/队满条件及操作过程
存储结构选择:
选择带空节点的循环链表:链式结构便于动态扩容(满足"入队可增空间"),循环设计可以复用出队节点空间(满足"出队空间重读使用"),仅需维护头指针(front)和尾指针(rear),保证操作O(1)复杂度
初始状态与队空/队满条件:
初始状态:front和rear均指向同一个空结点(无数据),空节点的next指向自身,形成循环
队空条件:front==rear(此时无有效数据结点)
队满条件:front==rear->next
rear的下一个结点为front,说明当前所有结点均存满数据,需新增空节点