学习视频 :第4章-决策树_哔哩哔哩_bilibili
西瓜书对应章节: 第四章 4.1;4.2
文章目录
- 决策树算法原理
-
-
-
- [- 逻辑角度](#- 逻辑角度)
- [- 几何角度](#- 几何角度)
-
-
- [ID3 决策树](#ID3 决策树)
-
-
-
- [- 自信息](#- 自信息)
- [- 信息熵 (自信息的期望)](#- 信息熵 (自信息的期望))
- [- 条件熵 ( Y 的信息熵关于概率分布 X 的期望)](#- 条件熵 ( Y 的信息熵关于概率分布 X 的期望))
- [- 信息增益](#- 信息增益)
- [- ID3 决策树](#- ID3 决策树)
- [- 问题](#- 问题)
-
-
- C4.5决策树
-
-
-
- [- 增益率](#- 增益率)
-
- [-- 属性固有值](#-- 属性固有值)
- [- 缺点](#- 缺点)
-
-
- [CART 决策树](#CART 决策树)
-
-
-
- [- 基尼值](#- 基尼值)
- [- 属性的基尼指数](#- 属性的基尼指数)
- [- CART 决策树的实际构造算法](#- CART 决策树的实际构造算法)
-
-
决策树算法原理
- 逻辑角度
if...else.. 语句的组合,不断的选择
- 几何角度
根据某种准则划分特征空间
最终目的:提高分类样本的纯度
ID3 决策树
- 自信息
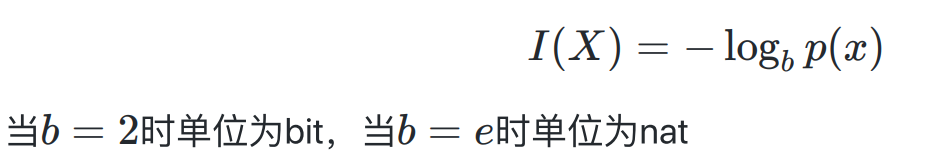
- 信息熵 (自信息的期望)
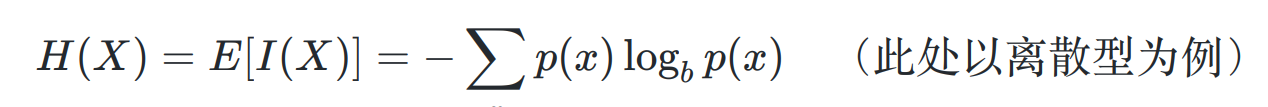
其中 X 作为随机变量,假设可能有 a, b, c 3种可能的状态:
- p(a|b|c)=1 是最确定的,信息熵最小
- p(a) = p(b) = p© 时可能性相同, X是最不确定的,信息熵最大
将样本类别标记视作随机变量,各个类别在样本集合中的占比视作各类别取值的概率,此时信息熵的 不确定性 可以转化为 集合内样本的纯度
- 条件熵 ( Y 的信息熵关于概率分布 X 的期望)
在已知 X 后 Y 的不确定性
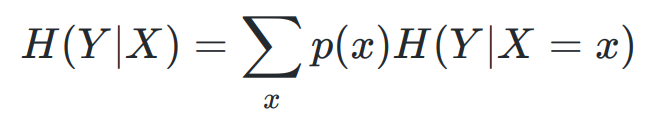
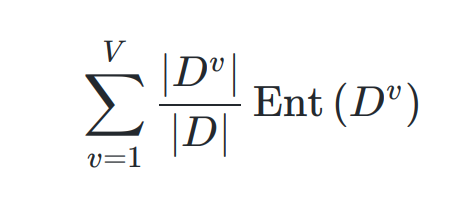
- 信息增益
已知属性特征 a 的取值后, y 的不确定减少的量
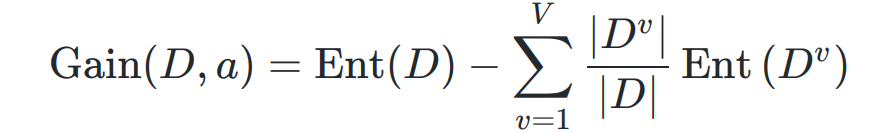
- ID3 决策树
以 信息增益 为准则选择划分属性的 决策树
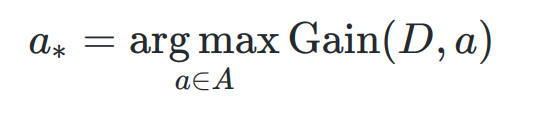
- 问题
信息增益 可能对取值数目多的属性有偏好 (比如 编号)
C4.5决策树
- 增益率
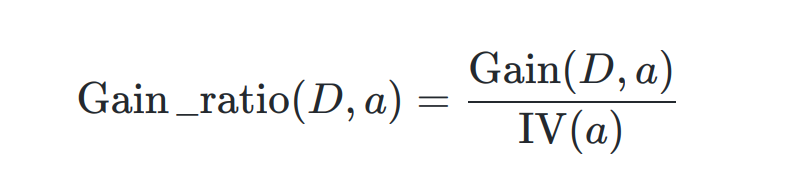
-- 属性固有值
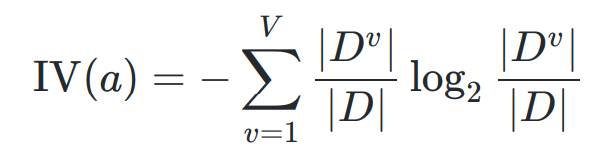
a 可能取值的个数 V 越多,则 通常其固有值 IV(a)越大
- 缺点
增益率可能对 取值数目少的属性有偏好
C45算法并未完全使用 "增益率"替代 "信息增益"。采用启发式算法:先选出信息增益高出平均水平 的属性,然后从中选择增益率最高的。
CART 决策树
- 基尼值
从样本集合D中随机抽取两个样本,其类别标记不一致的概率
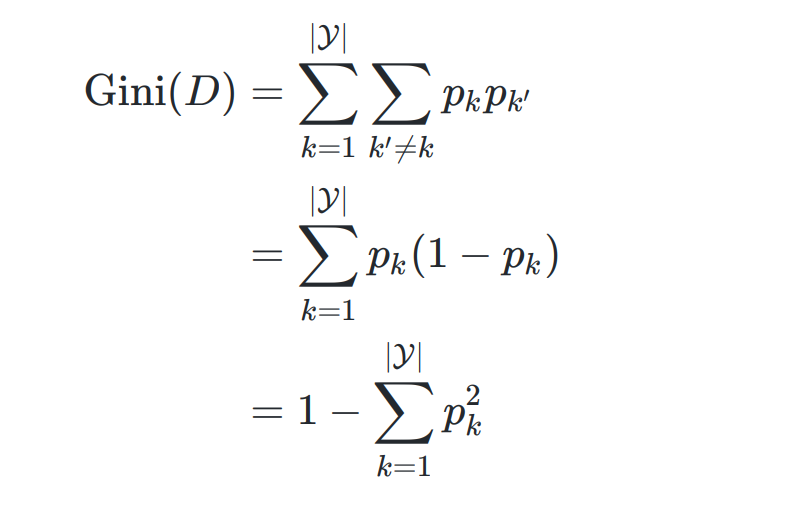
- 属性的基尼指数
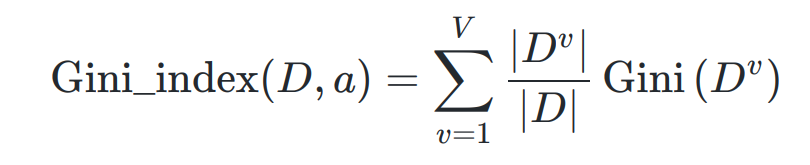
- CART 决策树的实际构造算法

