学习周报二十五

文章目录

• 摘要
• abstract
• 一、无监督学习
• • [1. PCA------主成分分析](#1. PCA——主成分分析)
• [二、 强化学习](#二、 强化学习)
• • [2.1 Q-learning算法------RL](#2.1 Q-learning算法——RL)
  • [2.2 RL与神经网络](#2.2 RL与神经网络)
• 三、推荐算法与神经网络结合代码实现
• 总结

摘要

学习了无监督学习（PCA）、强化学习（Q-learning）的核心原理，以及神经网络与推荐算法结合的实践实现。阐述 PCA 作为线性降维方法的原理、步骤、应用场景，分析其在大模型和深度神经网络中不适用的原因及有限应用场景；其次介绍强化学习的核心框架、Q-learning 算法的原理与贝尔曼更新方程，以及神经网络如何解决传统强化学习的维度灾难问题；最后通过完整的 PyTorch 代码实现 NeuMF 推荐模型，详细说明数据编码、负采样、二分类损失优化、HR/NDCG 评估等关键环节，展示了 GMF（线性交互）与 MLP（非线性交互）融合的推荐模型从数据处理到生成 Top-N 推荐的全流程。

abstract

Studied the core principles of unsupervised learning (PCA) and reinforcement learning (Q-learning), as well as the practical implementation of combining neural networks with recommendation algorithms. Explained the principles, steps, and application scenarios of PCA as a linear dimensionality reduction method, and analyzed the reasons why it is unsuitable for large models and deep neural networks, as well as its limited application scenarios. Next, introduced the core framework of reinforcement learning, the principles of the Q-learning algorithm, and the Bellman update equation, as well as how neural networks address the dimensionality curse in traditional reinforcement learning. Finally, implemented the NeuMF recommendation model with complete PyTorch code, providing detailed explanations of key steps such as data encoding, negative sampling, binary classification loss optimization, and HR/NDCG evaluation, demonstrating the full process of fusing GMF (linear interaction) and MLP (non-linear interaction) recommendation models from data processing to generating Top-N recommendations.

一、无监督学习

1. PCA------主成分分析

主成分分析是一种用于降维和数据压缩的统计方法，通过线性变换，将原始数据中可能相关的多个变量，转换为一组线性不相关的变量，称为"主成分"，同时尽可能保留原始数据的信息（方差）。

在无监督学习中，将多个数量的特征减少，减少存储和计算开销。

原理：

最大化方差。第一个主成分方向是数据方差最大的方向，即数据点在这个方向上最分散（信息量最大）。第二个主成分与第一个正交（垂直），并尽可能解释剩余方差中最大的部分，依此类推。

数学原理与步骤：

假设有 m 条数据，每条数据有 n 个特征（变量）。

步骤一：中心化：将每个特征的数据减去该特征的均值，使得数据的均值为0。这是为了消除量纲影响，使分析集中在数据的"形状"而非"位置"上。

步骤二：计算协方差矩阵：计算所有特征两两之间的协方差，得到一个 n x n 的协方差矩阵。这个矩阵描述了特征之间的线性相关关系和各自的方差。

步骤三：特征值分解：对协方差矩阵进行特征值分解，得到1）特征值：每个特征值的大小，对应了其主成分所携带的方差量。特征值越大，该主成分越重要。2）特征向量：每个特征值对应的特征向量，定义了主成分的方向。向量中的各个值，表示原始变量对该主成分的"贡献权重"，称为"载荷"。

步骤四：选择主成分：将特征值从大到小排序。计算每个主成分的方差贡献率（该主成分特征值 / 所有特征值之和）。计算累计方差贡献率。通常选择累计贡献率达到某个阈值（如80%、90%）的前 k 个主成分，作为降维后的新变量。

步骤五：生成新数据（得分）：将中心化后的原始数据矩阵，投影到选定的 k 个特征向量（主成分方向）上，得到一个新的 m x k 维数据矩阵，这就是降维后的数据，也称为主成分得分。

应用：

数据降维与可视化：将高维数据（如成百上千个特征）降至2维或3维，便于绘制图表，观察数据结构和模式。

数据压缩：用少数主成分代替大量原始变量，减少存储和计算开销。

去除噪声与冗余：通常认为方差小的主成分可能代表了噪声。去除它们可以起到去噪效果。同时，PCA能消除变量间的多重共线性。

特征提取：在图像识别、生物信息学等领域，将原始特征转换为数量更少、更具代表性的新特征。

探索性数据分析：了解数据中哪些方向（变量组合）的变化最重要。

大模型和现代深度神经网络中不适用PCA有多个原因：

1） 数据性质与结构：从结构化到非结构化。PCA最适合处理结构化、数值型、连续的数据，其方差-协方差结构是有意义的核心假设是，数据的主要信息（方差）存在于几个正交的线性方向组合中。大模型处理的是非结构化、高维、稀疏、离散的数据。

2）非线性与线性：PCA是一个线性变换。深度学习的核心优势：现代神经网络（全连接层、卷积层、注意力层）都引入了非线性激活函数，它们能够拟合极度复杂的非线性函数，从而学习数据中分层的、抽象的非线性特征表示。当面对图像、语言中的复杂模式时，PCA只能提供一个全局的、线性的最佳"视角"，而神经网络可以学习无数个局部的、非线性的"特征探测器"，并组合起来形成一个分层的理解。

3）维度与计算：PCA需要对 d x d 的协方差矩阵进行特征值分解，其中 d 是特征维度。当 d 极大时（一张1024x1024图像的展平维度超过100万），计算在内存和时间上都是不可行的。

4）PCA的目标：最大化重建误差最小化或投影方差最大化，本质上是一个信号处理/数据压缩的目标。大模型的目标：最大化任务性能（如预测下一个词、图像分类、机器翻译），需要保留对任务至关重要的语义信息，而这些信息未必与数据中的最大方差方向对齐。

5）上下文与顺序：从独立同分布到序列建模。PCA的假设：数据点是独立同分布的。它完全忽略数据的序列顺序或上下文依赖。大模型的核心能力：Transformer等架构的核心是自注意力机制，它显式地建模序列中所有元素之间的长距离依赖关系，对于理解语言、视频、代码等序列数据至关重要。

PCA在神经网络中的应用：

预处理与探索：在处理结构化数据输入神经网络前，可用PCA降维去噪。

分析与可视化：分析训练好的神经网络中间层的激活值，用PCA或t-SNE（非线性）将其降到2/3维进行可视化，理解网络学到了什么。

特定组件：在白化、某些归一化技术或模型压缩中，线性变换的思想有体现。

自监督学习中的应用：在一些自监督学习框架中，被集成进非线性框架。

二、 强化学习

强化学习：让一个智能体在一个环境 中通过试错 来学习如何采取行动，以最大化从环境中获得的累积奖励。

框架：

智能体：学习并做出决策的主体。

环境：智能体交互的外部世界，它对智能体的行动做出响应，并给出新的状态和奖励。

状态：环境在某一时刻的状况描述。

行动：智能体可以做出的选择。

奖励：环境在智能体执行一个行动后给出的即时反馈信号（一个标量数值）。

策略：智能体的行为函数，定义了在给定状态下应采取何种行动。这是智能体要学习的核心。

价值函数：对未来累积奖励的预测。它回答"从这个状态开始，未来总共能得多少分？"的问题。策略好的状态，价值就高。

模型（可选）：对环境动态的模拟，用于预测下一个状态和奖励。有模型学习和无模型学习是RL的两大分支。

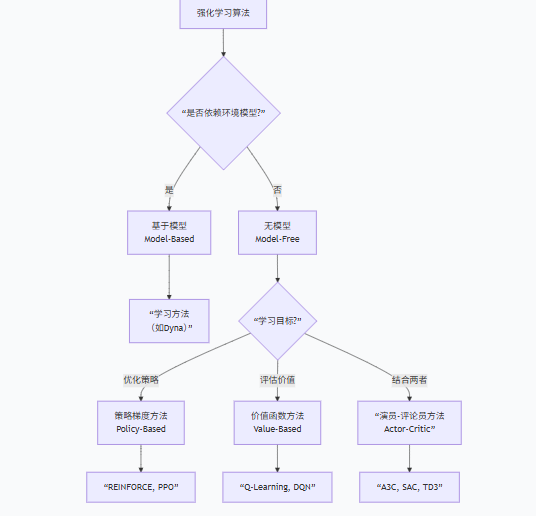
关键点：

价值函数是什么：对长期收益的预测，从当前状态（或采取当前动作后）开始，按照我当前的策略，未来我平均能获得多少累积奖励？两种主要类型：状态价值函数 V(s)：衡量一个状态的长期价值。动作价值函数 Q(s, a)：衡量在状态s下采取特定动作a的长期价值。这是Q-Learning等算法的核心。

作用：价值函数是策略优劣的"裁判"。智能体通过学习价值函数来间接改进策略（例如，选择Q值最高的动作）。

模型是什么：智能体对环境动态的认知。它是一个预测器，包含两部分：状态转移预测：给定状态 s 和动作 a，预测下一个状态 s' 的概率。奖励预测：预测即时奖励 r。

作用：如果智能体有一个好的环境模型，它就可以在内心进行模拟和规划，而不必完全依赖实际试错。引出了有模型学习和 无模型学习。

2.1 Q-learning算法------RL

Q(s, a)：我们要学习的函数，称为动作价值函数。它是在状态 s 下执行动作 a 所能获得的最大期望累积奖励。

Q-Table：表格，行代表所有可能的状态 s，列代表所有可能的动作 a。每个单元格存储的就是 Q(s, a)。开始时通常是随机初始化或全零。

贝尔曼方程: Q ( s t , a t ) = Q ( s t , a t ) + α ∗ [ r t + γ ∗ m a x a ( Q ( s t + 1 , a ) ) − Q ( s t , a t ) ] Q(s_t, a_t) =Q(s_t, a_t) + α * [ r_t + γ * max_{a}(Q(s_{t+1}, a)) - Q(s_t, a_t) ] Q(st,at)=Q(st,at)+α∗[rt+γ∗maxa(Q(st+1,a))−Q(st,at)].
Q ( s t , a t ) Q(s_t, a_t) Q(st,at)：在时间 t，状态 s t s_t st下，执行动作 a t a_t at 的旧Q值。

α：学习率。取值范围 (0, 1]。控制新信息覆盖旧信息的程度。α=1表示完全用新估计替换旧值；α较小则更新缓慢、稳定。

... \]：时序差分误差。这是"现实"与"预期"的差距，是驱动的学习信号。 r t r_t rt：即时奖励。执行动作 a_t 后环境直接给予的反馈。 γ：折扣因子。取值范围 (0, 1\]。代表对未来奖励的重视程度。γ=0 表示智能体只关心眼前利益；γ 接近1表示智能体非常有远见。 m a x a ( Q ( s t + 1 , a ) ) max_{a}(Q(s_{t+1}, a)) maxa(Q(st+1,a))：在下一个状态 s_{t+1} 下，所有可能动作中最大的Q值。这代表了我们对未来的"最佳预期"。 r t + γ ∗ m a x a ( Q ( s t + 1 , a ) ) r_t + γ \* max_{a}(Q(s_{t+1}, a)) rt+γ∗maxa(Q(st+1,a))：这就是 "目标值"或"现实"。它由两部分组成：立即得到的奖励 + 对未来最优路径的折现估计。 − Q ( s t , a t ) - Q(s_t, a_t) −Q(st,at)：这是我们旧的预期。目标值减去旧预期，就得到了误差。 =：整个公式的意义是：用当前的"现实"与"预期"的误差，按一定比例（α）来修正我们对 Q(s_t, a_t) 的估计，使其更接近真实价值。 总结：新的估计 = 旧的估计 + 学习率 \* （即时奖励 + 折扣因子 \* 未来最佳估计 - 旧的估计）。 观察更新公式中的 m a x a ( Q ( s t + 1 , a ) ) max_{a}(Q(s_{t+1}, a)) maxa(Q(st+1,a))，用的是下一个状态所有动作中最大的Q值来更新当前Q值。 "目标策略"：是一个完全贪婪的策略（总是选Q值最大的动作）。 "行为策略"：通常是ε-贪心策略（有时随机探索）。 利用：选择当前已知最好的动作（argmax Q）。目的是获得即时高回报。 探索：随机选择动作。目的是尝试可能更好的新选择，避免陷入局部最优。 ε 控制探索概率。通常开始时 ε 较高（多探索），随着学习进行逐渐降低（多利用）。 二者可以不同。意味着Q-Learning可以在遵循一个探索性策略（行为策略）进行行动的同时，却学习着另一个更优的贪婪策略（目标策略）。非常高效。 Q-Learning是连接经典表格强化学习与深度强化学习的桥梁，其核心思想：通过时序差分误差和贝尔曼最优方程来迭代更新价值估计仍是深度RL算法的基石。 ### 2.2 RL与神经网络 在经典RL中，面对一个根本性限制：状态和动作空间必须是离散且低维的。我们用一张表（如Q-Table）来存储每个状态-动作对的价值。但当状态是像素画面，或动作是连续值时，表格方法彻底失效。有两个问题：维度灾难：表格大小随维度指数增长，无法存储。泛化问题：无法对未见过但相似的状态进行推理。 神经网络的核心作用就是作为一个万能函数逼近器，用一组参数（权重）来近似表示RL中那些关键但复杂的函数：近似价值函数 Q(s, a; θ) 或 V(s; θ)；近似策略函数 π(a\|s; θ)； 这里的 θ 就是神经网络的权重。网络输入是状态 s（甚至可以直接是原始像素），输出就是我们想要的Q值、价值或动作概率分布。 神经网络作为价值网络解决"评估"问题：近似动作价值函数 Q(s,a) 或状态价值函数 V(s)。输入：环境状态 s（例如，游戏的4帧画面堆叠）。输出：如果输出V(s)，是一个标量，代表该状态的长期价值。如果输出Q(s,a)，可以是一个向量，每个元素代表在该状态下执行某个离散动作的Q值。 神经网络作为策略网络 -\> 解决"决策"问题作用：直接参数化并输出策略 π(a\|s)。输入：状态 s。输出：离散动作：一个概率向量，例如 \[0.7, 0.2, 0.1\]，分别代表"左"、"右"、"开火"的概率。连续动作：可以直接输出动作值（如方向盘角度），或输出一个高斯分布的均值和方差（用于探索）。 神经网络作为模型网络解决"想象"问题作用：学习环境的动态模型，即预测下一个状态 s' 和奖励 r。输入：当前状态 s 和动作 a。输出：预测的下一个状态 ŝ' 和预测的奖励 ř。 强化学习与神经网络联系： 强化学习定义了问题的框架（智能体通过试错最大化长期奖励），而神经网络提供了解决这个框架中核心函数（策略、价值、模型）的强大工具。 没有神经网络，RL只能解决"玩具级"问题；没有RL的框架，神经网络只是一个静态的函数拟合器。二者的结合（深度强化学习）催生了能够在复杂环境中自主学习决策的智能体。 ## 三、推荐算法与神经网络结合代码实现 下面代码实现推荐算法与神经网络相结合示例：采用的是随机数据进行训练与测试。 NeuMF 推荐模型，通过融合 GMF（捕捉线性交互）和 MLP（捕捉非线性交互），对用户 - 物品交互进行评分预测，最终实现 Top-N 推荐。 步骤：数据编码（解决 ID 不连续问题）→ 负采样（构建正负样本对）→ 模型训练（二分类损失优化）→ 评估（HR/NDCG 指标）→ 推荐（预测用户对所有物品的得分并排序）。 ```J import numpy as np import pandas as pd import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import Dataset, DataLoader from sklearn.model_selection import train_test_split # 补全缺失的导入 from sklearn.metrics import accuracy_score from tqdm import tqdm # 生成模拟数据（MovieLens风格） np.random.seed(42) num_users = 1000 num_items = 500 ratings = pd.DataFrame({ 'user_id': np.random.randint(0, num_users, 100000), 'item_id': np.random.randint(0, num_items, 100000), 'rating': np.random.randint(1, 6, 100000) # 评分1-5 }) # 数据预处理 def load_data(ratings, test_size=0.2): train_data, test_data = train_test_split(ratings, test_size=test_size, random_state=42) # 用户/物品映射（修复变量命名冲突问题） user_unique = ratings['user_id'].unique() item_unique = ratings['item_id'].unique() user_encoder = {u: idx for idx, u in enumerate(user_unique)} item_encoder = {i: idx for idx, i in enumerate(item_unique)} # 映射编码，避免SettingWithCopyWarning train_data = train_data.copy() test_data = test_data.copy() train_data['user'] = train_data['user_id'].map(user_encoder) train_data['item'] = train_data['item_id'].map(item_encoder) test_data['user'] = test_data['user_id'].map(user_encoder) test_data['item'] = test_data['item_id'].map(item_encoder) return train_data, test_data, len(user_encoder), len(item_encoder), user_encoder, item_encoder # 加载数据并获取编码器 train_data, test_data, num_users, num_items, user_encoder, item_encoder = load_data(ratings) # 构建反向映射（用于负采样） user_decoder = {v: k for k, v in user_encoder.items()} item_decoder = {v: k for k, v in item_encoder.items()} class NCFDataset(Dataset): def __init__(self, data, num_negatives=4): self.users = data['user'].values self.items = data['item'].values self.labels = data['rating'].values self.num_negatives = num_negatives # 负采样（修复用户ID映射错误） self.negatives = [] item_pool = set(range(num_items)) # 编码后的物品ID池 for idx in range(len(self.users)): u = self.users[idx] pos_item = self.items[idx] # 获取原始用户ID，找到该用户真实交互过的物品（编码后） original_u = user_decoder[u] interacted_items = ratings[ratings['user_id'] == original_u]['item_id'].tolist() interacted_items_encoded = [item_encoder[i] for i in interacted_items if i in item_encoder] # 负样本：从未交互过的物品中随机选 candidate_neg = list(item_pool - set(interacted_items_encoded) - {pos_item}) # 处理候选集不足的情况（避免采样失败） if len(candidate_neg) < num_negatives: neg_items = np.random.choice(candidate_neg, size=num_negatives, replace=True) else: neg_items = np.random.choice(candidate_neg, size=num_negatives, replace=False) self.negatives.append(neg_items) def __len__(self): return len(self.users) def __getitem__(self, idx): user = self.users[idx] pos_item = self.items[idx] neg_items = self.negatives[idx] return torch.tensor(user, dtype=torch.long), \ torch.tensor(pos_item, dtype=torch.long), \ torch.tensor(neg_items, dtype=torch.long) class GMF(nn.Module): def __init__(self, user_num, item_num, latent_dim): super().__init__() self.user_emb = nn.Embedding(user_num, latent_dim) self.item_emb = nn.Embedding(item_num, latent_dim) # 初始化嵌入层（提升训练稳定性） nn.init.normal_(self.user_emb.weight, std=0.01) nn.init.normal_(self.item_emb.weight, std=0.01) def forward(self, u, i): u_emb = self.user_emb(u) i_emb = self.item_emb(i) pred = torch.mul(u_emb, i_emb) # 元素乘，shape: [batch_size, latent_dim] return pred # 不提前压缩维度，留给NeuMF处理 class MLP(nn.Module): def __init__(self, user_num, item_num, layers, dropout): super().__init__() emb_dim = layers[0] // 2 # 保证拼接后维度匹配 self.user_emb = nn.Embedding(user_num, emb_dim) self.item_emb = nn.Embedding(item_num, emb_dim) # 初始化嵌入层 nn.init.normal_(self.user_emb.weight, std=0.01) nn.init.normal_(self.item_emb.weight, std=0.01) # 构建MLP层 mlp_layers = [] input_dim = layers[0] # 拼接后维度：emb_dim*2 for out_dim in layers[1:]: mlp_layers.append(nn.Linear(input_dim, out_dim)) mlp_layers.append(nn.ReLU()) mlp_layers.append(nn.Dropout(dropout)) input_dim = out_dim self.mlp = nn.Sequential(*mlp_layers) def forward(self, u, i): u_emb = self.user_emb(u) i_emb = self.item_emb(i) x = torch.cat([u_emb, i_emb], dim=-1) # shape: [batch_size, emb_dim*2] return self.mlp(x) # shape: [batch_size, layers[-1]] class NeuMF(nn.Module): def __init__(self, user_num, item_num, latent_dim=64, mlp_layers=[64, 32], dropout=0.2): super().__init__() self.gmf = GMF(user_num, item_num, latent_dim) self.mlp = MLP(user_num, item_num, mlp_layers, dropout) # 融合层：GMF输出维度(latent_dim) + MLP输出维度(mlp_layers[-1]) self.fc = nn.Linear(latent_dim + mlp_layers[-1], 1) nn.init.normal_(self.fc.weight, std=0.01) nn.init.constant_(self.fc.bias, 0.0) def forward(self, u, i): gmf_out = self.gmf(u, i) # [batch_size, latent_dim] mlp_out = self.mlp(u, i) # [batch_size, mlp_layers[-1]] concat = torch.cat([gmf_out, mlp_out], dim=-1) # 维度拼接 pred = torch.sigmoid(self.fc(concat)).squeeze(-1) # 压缩到[batch_size] return pred # 超参数设置 batch_size = 256 epochs = 20 lr = 0.001 num_negatives = 4 device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') print(f"Using device: {device}") # 数据加载器（修复训练集/测试集混用问题） train_dataset = NCFDataset(train_data, num_negatives=num_negatives) test_dataset = NCFDataset(test_data, num_negatives=num_negatives) train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True) test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False) # 模型初始化 model = NeuMF(num_users, num_items, latent_dim=64, mlp_layers=[64, 32], dropout=0.2).to(device) criterion = nn.BCELoss() # 二分类损失（正样本1，负样本0） optimizer = optim.Adam(model.parameters(), lr=lr) # 训练循环 best_hr = 0 for epoch in range(epochs): model.train() total_loss = 0 pbar = tqdm(train_loader, desc=f"Epoch {epoch + 1}/{epochs}") for u, pos_i, neg_i in pbar: u, pos_i, neg_i = u.to(device), pos_i.to(device), neg_i.to(device) # 正样本预测 pos_pred = model(u, pos_i) # 负样本预测（处理负样本的批量维度） neg_pred = [] for i in range(num_negatives): neg_pred.append(model(u, neg_i[:, i])) neg_pred = torch.stack(neg_pred, dim=1).mean(dim=1) # 负样本预测取平均 # 损失计算 pos_label = torch.ones_like(pos_pred) neg_label = torch.zeros_like(neg_pred) loss = criterion(pos_pred, pos_label) + criterion(neg_pred, neg_label) optimizer.zero_grad() loss.backward() optimizer.step() total_loss += loss.item() pbar.set_postfix({"Loss": f"{loss.item():.4f}"}) avg_loss = total_loss / len(train_loader) print(f"Epoch {epoch + 1}/{epochs}, Average Loss: {avg_loss:.4f}") # 评估（修复HR/NDCG计算逻辑） model.eval() hits, ndcgs = [], [] with torch.no_grad(): for u, pos_i, _ in test_loader: u, pos_i = u.to(device), pos_i.to(device) # 对每个用户，预测所有物品的得分 for idx in range(len(u)): single_u = u[idx].repeat(num_items) all_items = torch.arange(num_items).to(device) scores = model(single_u, all_items) # Top-K推荐 top_k = torch.topk(scores, 10).indices.cpu().numpy() target_item = pos_i[idx].cpu().item() # 计算Hit Rate hits.append(1 if target_item in top_k else 0) # 计算NDCG if target_item in top_k: rank = np.where(top_k == target_item)[0][0] + 1 # 排名从1开始 ndcgs.append(1 / np.log2(rank + 1)) else: ndcgs.append(0) hr = np.mean(hits) ndcg = np.mean(ndcgs) print(f"Evaluation - Hit Rate@10: {hr:.4f}, NDCG@10: {ndcg:.4f}") if hr > best_hr: torch.save(model.state_dict(), 'best_model.pth') best_hr = hr print(f"Best model saved (HR: {best_hr:.4f})") # 推荐函数 def recommend(user_id, top_n=10): """ 为用户推荐物品 :param user_id: 原始用户ID（不是编码后的ID） :param top_n: 推荐数量 :return: 推荐物品ID（原始）和得分 """ model.eval() # 转换为编码后的用户ID if user_id not in user_encoder: return [] u_encoded = torch.tensor(user_encoder[user_id], dtype=torch.long).to(device) all_items_encoded = torch.arange(num_items, dtype=torch.long).to(device) with torch.no_grad(): # 预测所有物品得分 u_batch = u_encoded.repeat(num_items) scores = model(u_batch, all_items_encoded).cpu().numpy() # 按得分排序，取Top-N top_indices_encoded = np.argsort(scores)[::-1][:top_n] # 转换回原始物品ID recommendations = [] for idx in top_indices_encoded: original_item_id = item_decoder[idx] recommendations.append((original_item_id, scores[idx])) return recommendations # 示例：为用户0推荐前10个物品 print("\\nTop recommendations for user 0:") recommendations = recommend(0, 10) for item, score in recommendations: print(f"Item {item} - Score: {score:.4f}") ``` 负采样：正样本：用户和物品之间存在真实的交互行为（比如代码中用户给某部电影打过分，这个 (user, item) 对就是正样本）。负样本：用户和物品之间没有任何交互行为（比如代码中用户从没给某部电影打过分，这个 (user, item) 对就是负样本）。推荐系统的原始数据有一个典型问题：极度稀疏。 海量负样本中随机选一小部分，减少训练数据量，提升训练效率；构建均衡的正负样本集，让模型学会区分 "用户喜欢的物品" 和 "用户不感兴趣的物品"。 二分类交叉熵损失： L o s s = − \[ y ∗ l o g ( y \^ ) + ( 1 − y ) ∗ l o g ( 1 − y \^ ) \] Loss=-\[y\*log(\\hat{y})+(1-y)\*log(1-\\hat{y})\] Loss=−\[y∗log(y\^)+(1−y)∗log(1−y\^)\]。 优化：调整参数降低损失，模型训练的核心动作：通过算法（Adam 优化器）不断调整模型的参数（嵌入层的权重、MLP 的权重），让损失值越来越小。从损失值出发，倒着计算每个参数的梯度；优化器更新：按照梯度方向调整参数，让下一次预测的损失更小。  ## 总结 PCA 是线性降维方法，适用于结构化数值型数据的压缩、去噪与可视化，无法处理非结构化 / 序列数据难以适配大模型和深度神经网络。强化学习以智能体与环境交互、最大化累积奖励为目标，神经网络作为函数逼近器，解决了传统 RL 的维度灾难问题，结合形成深度强化学习，赋能复杂环境的自主决策。 代码方面灭有找到合适的数据集去构建一个模型，只用了随机数据。 下周计划对代码进行改进学习。看一个项目的完整论文。