【LeetCode】十、二分查找法：寻找峰值 + 二维矩阵的搜索

文章目录

[1、二分查找法 Binary Search](#1、二分查找法 Binary Search)
2、leetcode704：二分查找
3、leetcode35：搜索插入位置
4、leetcode162：寻找峰值
5、leetcode74：搜索二维矩阵

1、二分查找法 Binary Search

找一个数，有序的情况下，直接遍历找，时间复杂度为O(n)，用二分法，一半一半的砍着找，则时间复杂度为O(log n)，更优

核心：左、中、右三个指针的移动

2、leetcode704：二分查找

注意下面对中间指针的求法，不写 (l + r ) / 2，写成 l + (r - l) / 2，二者通分后值一样，但l + r可能超出int的最大值，后者这种写法则可规避这个问题。且除二可以改为位运算 >> 1，其快于除法运算，注意右移的运算优先级很低，要加括号（a + b >> c 会首先执行加法 a + b，然后将结果右移 c 位）

java 复制代码

public class P704 {

    public static int binarySearch(int[] array, int value) {
        if (array == null || array.length == 0) {
            return 0;
        }
        int left = 0;
        int right = array.length - 1;
        int mid;
        while (left <= right) {
            mid = left + (right - left) / 2;
            if (array[mid] > value) {
                // 右边半截不要了
                right = mid - 1;
            } else if (array[mid] < value) {
                // 左边半截不要了
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

测试：

java 复制代码

public class P704 {
    public static void main(String[] args) {
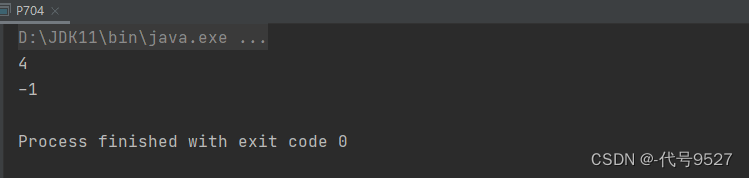
        int[] num = {-1, 0, 3, 5, 9, 12};
        System.out.println(binarySearch(num, 9));
        System.out.println(binarySearch(num, 10));
    }

}

3、leetcode35：搜索插入位置

第一个想法是：先普通的二分查找value，返回-1后，说明不存在，那就再遍历这个数组，用双指针，当p1的值 < value && p2的值 > value时，return p1 + 1，但这样应该是复杂了

换个想法，只需调整下普通的二分查找：这题要求找值target，有就返回下标索引，无就返回插入后的下标索引，因此，这题要找第一个大于等于target的值的下标索引，如果有等于target的，那返回其下标，如果不存在，那就要插入到第一个比target大的值的位置，第一个大的值的下标则往后移动一位。

java 复制代码

public class P35 {
    
    public static int searchOrInsert(int[] array, int target) {
        if (array == null || array.length == 0) {
            return 0;
        }
        int left = 0;
        int right = array.length - 1;
        int ans = array.length;
        while (left <= right) {
            int mid = ((right - left) >> 1) + left;
            if (target == array[mid]) {
                // 如果有，直接返回
                return mid;
            } else if (target < array[mid]) {
                // 如果mid大于target，存一下mid的值
                // 此时mid是大于target的值，但不一定是第一个大于target的值
                ans = mid;
                right = mid - 1;
            } else {
                // 左指针右移，说明target很大，极限时，插入到末尾，此时return array.length即末尾
                left = mid + 1;
            }
        }
        return ans;
    }
}

4、leetcode162：寻找峰值

一头一尾是负无穷，所以，即使是1，2，3，4这个输入，也有峰值：4

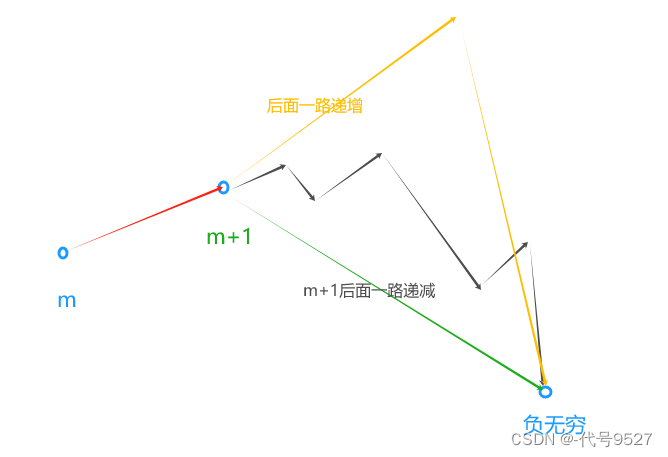
m+1 > m时，m+1到right之间一定有一个峰值，不论m的左侧是单增、单减、波浪起伏。此时可把左指针移动到m+1的位置，减少搜索范围。

java 复制代码

public class P162 {

    public static int getPeak(int[] array) {
        if (null == array || array.length == 0){
            return -1;
        }
        int left = 0;
        int right = array.length - 1;
        // 这儿不能允许left==right,否则当left=right=末尾元素时，mid也就是末尾元素，mid+1就越界了
        while (left < right) {
            int mid = left + ((right - left) >> 1);
            //说明mid和mid+1两个点，从左到右是下降的，mid自身或者mid的左边可能有峰值
            if (array[mid] > array[mid + 1]) {
                right = mid;
            } else {
                // 一定有个峰值出现在mid+1到right之间
                left = mid + 1;
            }
        }
        return left;
    }
}

5、leetcode74：搜索二维矩阵

如题，这样特点的矩阵，本身就是递增的，如图中的1、3、5、7、10、11、16......

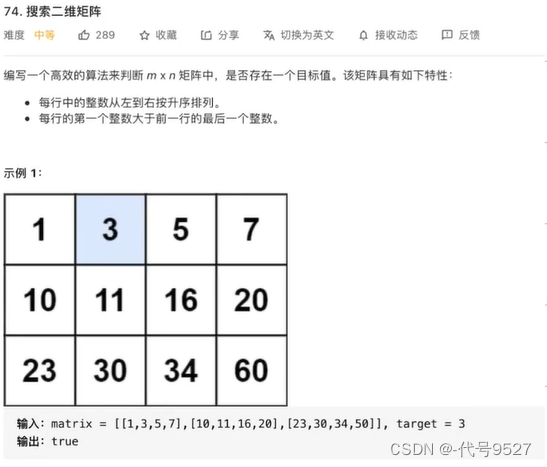
在有序的集合里找一个数字，可以二分查找。但现在虽然有序，却不是集合，是一个二维数组，那把矩阵拍平后就是一个简单的二分查找了。把这个矩阵（二维数组）拍平有两种思路：

直接遍历二维数组，把每个元素装入一位数组，但这样得两层for，时间复杂度太高
思想上拍平，将二维数组的索引，和一维数组建立联系

考虑将二维数组的索引（x，y）转为一维的索引i，。关于二维索引和一维索引的相互转换，发现：

将二维索引(x，y)和一维索引 i 标出来，得出：一维索引的坐标 i = x * 列总数 + y

java 复制代码

如上面总列数为4，(0,0)对应的一维坐标正好是 0 * 4 + 0 = 0

如此，不用遍历二维数组，就可将矩阵的每个数都对应一个一维坐标 。二分法时，起始左指针 = 0，右指针 = 行数 × 列数 - 1（即总元素数），计算出mid后，无法根据mid索引在二维数组中取值，需要将一维坐标再倒回去，x = i / 列总数，y = i % 总列数

java 复制代码

public class P74 {

    public boolean matrixSearch(int[][] matrix, int target) {
        if (null == matrix || matrix.length == 0) {
            return false;
        }
        // 行数
        int row = matrix.length;
        // 列数
        int col = matrix[0].length;
        // 左右指针起始位置
        int left = 0;
        int right = row * col - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            // 无法根据一维的mid索引在二维数组中取值，需要将一维坐标再倒回去
            // x = i / 列总数 ，y = i % 总列数
            int element = matrix[mid / col][mid % col];
            if (target == element) {
                return true;
            } else if (target < element) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }

        }
        return false;
    }
}