文章目录
- [2.3 推导](#2.3 推导)
-
- [2.3.1 直接推导/直接规约](#2.3.1 直接推导/直接规约)
- [2.3.2 推导/规约](#2.3.2 推导/规约)
- [2.3.3 规范推导](#2.3.3 规范推导)
- [2.4 句型和句子](#2.4 句型和句子)
- [2.5 语言](#2.5 语言)
- [2.6 文法的分类](#2.6 文法的分类)
-
- [2.6.1 0型文法](#2.6.1 0型文法)
- [2.6.2 1型文法](#2.6.2 1型文法)
- [2.6.3 2型文法](#2.6.3 2型文法)
- [2.6.4 3型文法](#2.6.4 3型文法)
- [2.7 推导语法树的构造](#2.7 推导语法树的构造)
- [2.8 递归规则和递归文法](#2.8 递归规则和递归文法)
- [2.9 文法的二义性](#2.9 文法的二义性)
-
- [2.9.1 有关文法的实用限制](#2.9.1 有关文法的实用限制)
2.3 推导
2.3.1 直接推导/直接规约
简言之,一步直接退换
例如:有文法G[S]:S→0S1,S→01
有直接推导 0S1⇒0011
有直接推导 0S1⇒00S11
有直接推导S⇒0S1
2.3.2 推导/规约
若存在直接推导序列,符号串一直进行直接推导,直到没有非终结符号时,推导就必须终止

推导例题:
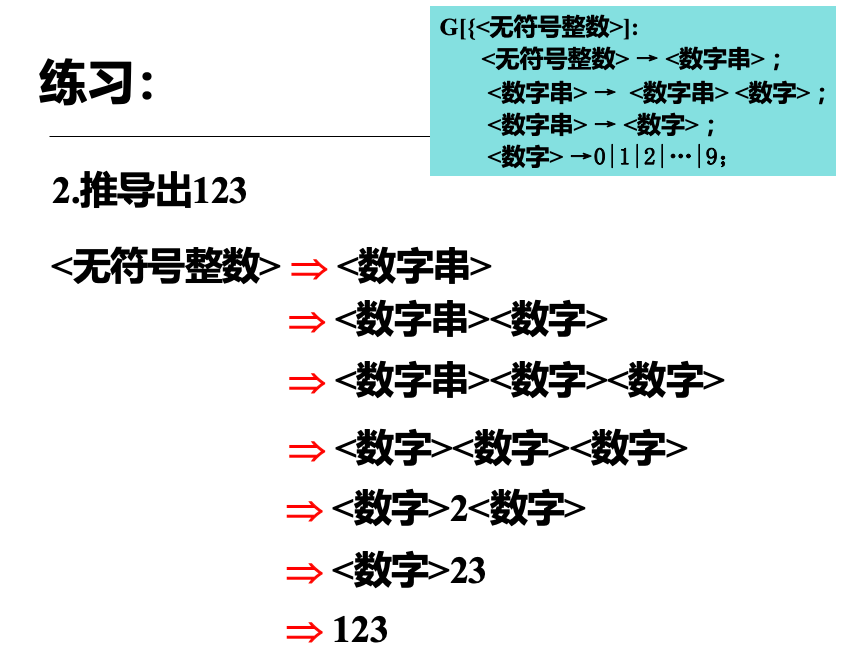
2.3.3 规范推导
规范推导也叫最右推导,每步只变换符号串中最右边的非终结符,直到推导结束
2.4 句型和句子
1.句型
有文法G[Z],若Z 0步以上推导出x,则称x是文法G的句型
2.句子
有文法G[Z],若Z 1步以上推导出且x都是终结符号,则称x是文法G的句子
例:G[S],S→0S1,S→01
S⇒0S1⇒00S11⇒000S111⇒00001111
G的句型S,0S1,00S11,000S111,00001111等
G的句子00001111等
|---------|
| 识别符号是句型 |
注意:
1️⃣句子是特殊的句型
2️⃣规范推导产生的句型为规范句型
3️⃣每个句子都有一个规范推导
4️⃣并非每一个句型都有规范推导
练习:

2.5 语言
语言是句子的集合,文法G生成的语言记为L(G(Z)),他是文法G(Z)的一切句子的集合
注意:给定一文法,能从结构上唯一确定其语言,给定一种语言,能确定其文法,但不唯一
我的理解,文法是信息,语言就类似于汉语,英语这种,给我一个信息,我想把翻译出来,用汉语那就是唯一确定的,如果给我一个汉语写的信息,我还可以把用日语,英语翻译,再变成信息。
例:

2.6 文法的分类
对文法中的不同规则施加不同的限制,将文法和语言分为四大类
0型文法:0型语言或短语结构语言
1型文法:1型语言或上下文有关语言
2型文法:2型语言或上下文无关语言
2型文法是程序设计语言语法规则
3型文法:3型语言或正则语言
3型文法是程序设计语言构词规则
2.6.1 0型文法
对产生式基本无限制
2.6.2 1型文法
文法左部符号个数不超过右部符号个数
2.6.3 2型文法
任意产生式A→B,A属于非终结符号,B终结不终结都可
说明:描述程序设计语言的语法规则
2.6.4 3型文法
任意产生式A→B,都为A→aB,A→a,这种形式,比较严格
通常用来描述单词结构,其中包括标识符,常量,运算符,界符等
总结:四种文法的关系是逐级包括的,限制少的包含限制多的
2.7 推导语法树的构造
跳转到编译原理大题专栏:【编译原理必考大题】 推导构建语法树,写出语法树的短语,简单短语和句柄
2.8 递归规则和递归文法
递归规则指的是在规则右部含有和左部相同符号的规则,如U→xUy;其中这种U→Uy称为左递归,还有右递归。
递归文法使人们能用有穷的文法刻画无穷语言。
2.9 文法的二义性
若一个文法存在某个句子或句型,它存在两棵不同的语法树,则称该句子或句型是二义性的,对应的文法也是二义性的。
|----------------------------------------------------|
| 二义性不可判定,从底向上看,二义性意味着句柄不唯一,解决二义性的方法是,加以限制,人为避免产生二义性 |
2.9.1 有关文法的实用限制
-
多余规则:指文法中任何句子的推导都不会用到的规则,若有则删去
-
不可到达:非终结符不再任何规则的右部出现,称该非终结符为不可到达
-
不可终止:由它不能退出终结符号串,称该非终结符为不可终止

-