1.图像卷积、步长、填充
图像卷积
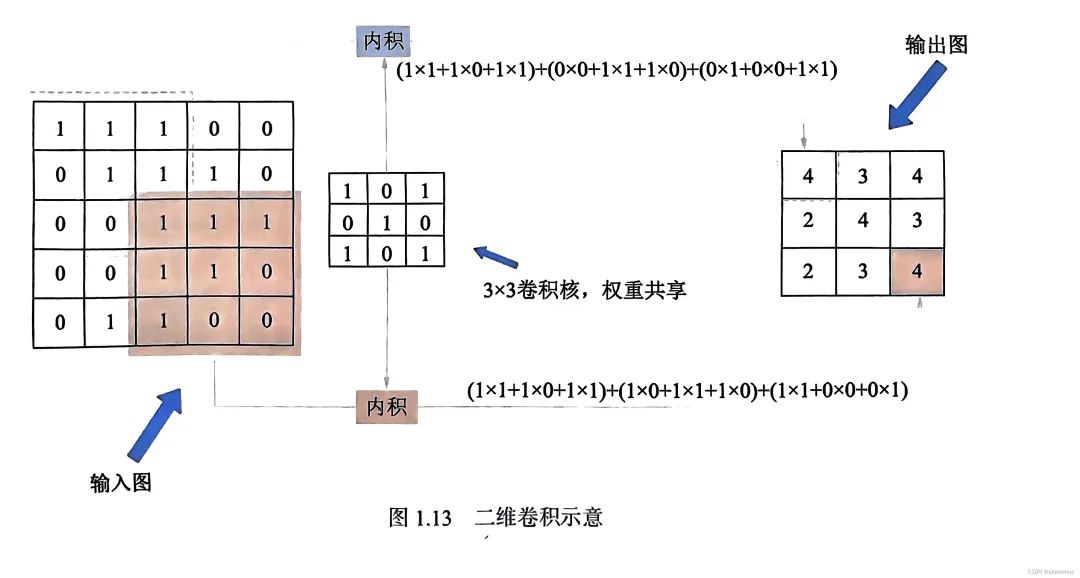
卷积核矩阵在一个原始图像矩阵上 "从上往下、从左往右"滑动窗口进行卷积计算,然后将所有结果组合到一起得到一个新的矩阵的过程。
-
用一个相同的卷积核对整幅图像进行进行卷积操作,相当于对图像做一次全图滤波,符合卷积核特征的部分得到的结果比较大,不符合卷积核特征的部分得到的结果比较小,因此卷积操作后的结果可以较好地表征该区域符合卷积核所描述的特征的程度。
-
一次完整的卷积会选出图片上所有符合这个卷积核的特征。
-
如果将大量图片作为训练集,则卷积核最终会被训练成有意义的特征。例如,识别飞机,卷积核可以是机身或者飞机机翼的形状等。
步长(Stride)
卷积核在图像上移动的步子,不同的步长会影响输出图的尺寸。更大的步长意味着空间分辨率的快速下降。
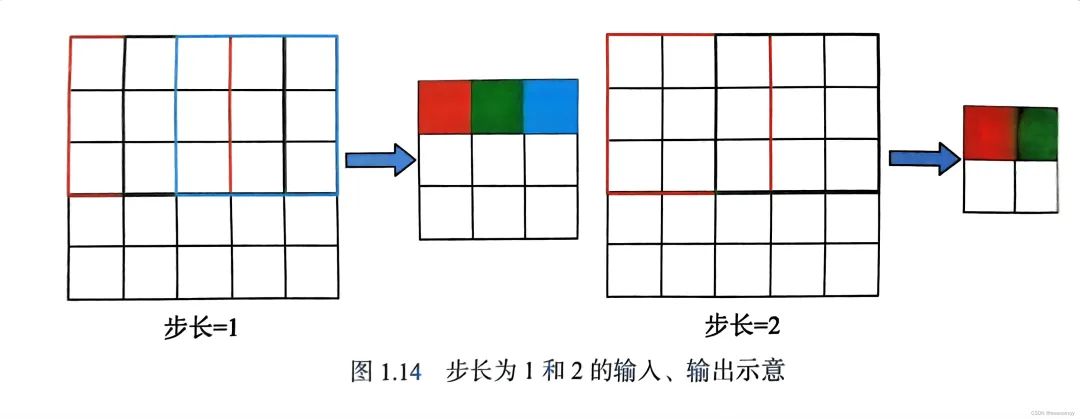
输入图都是5×5,卷积核大小都是3×3。
-
Stride=1,卷积后的结果=3×3
-
Streide=2,卷积后的结果=2×2
填充(Padding)
为了更好地控制输入和输出图的大小,一般会对输入进行填充操作。填充操作就是在原来输入图的边界外进行扩充,使其变得更大,卷积后的结果也会更大。通常会设计卷积网络层时小心地进行填充,从而精确地控制输入图和输出图的大小关系。
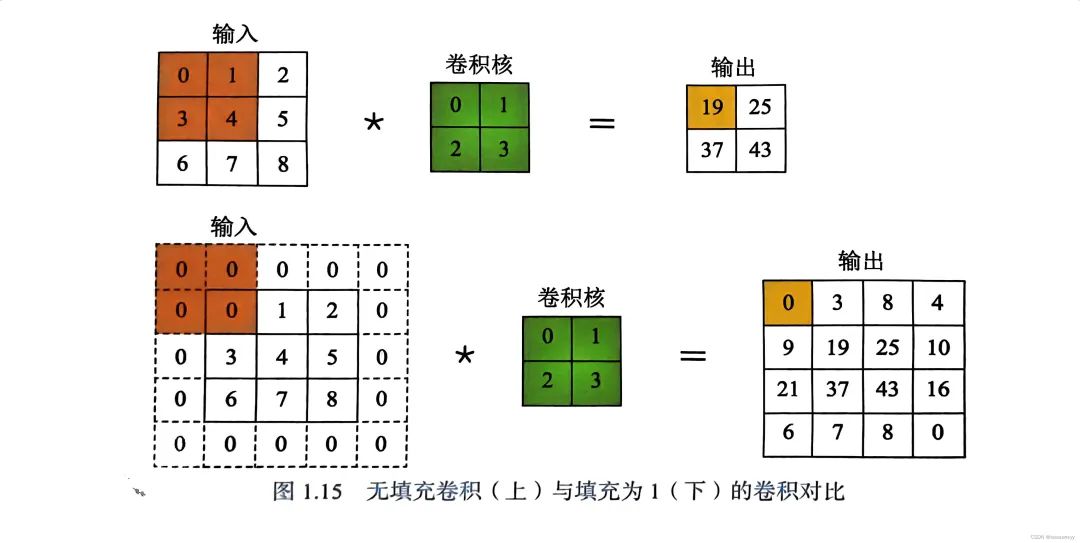
无填充和有填充卷积的对比结果。
-
没有填充:输入为3×3的图,输出为2×2的图,分辨率降低。
-
有填充:在原图周围填充一行或一列的0,输出为4×4,分辨率没有降低。
2.特征图与多通道卷积
特征图
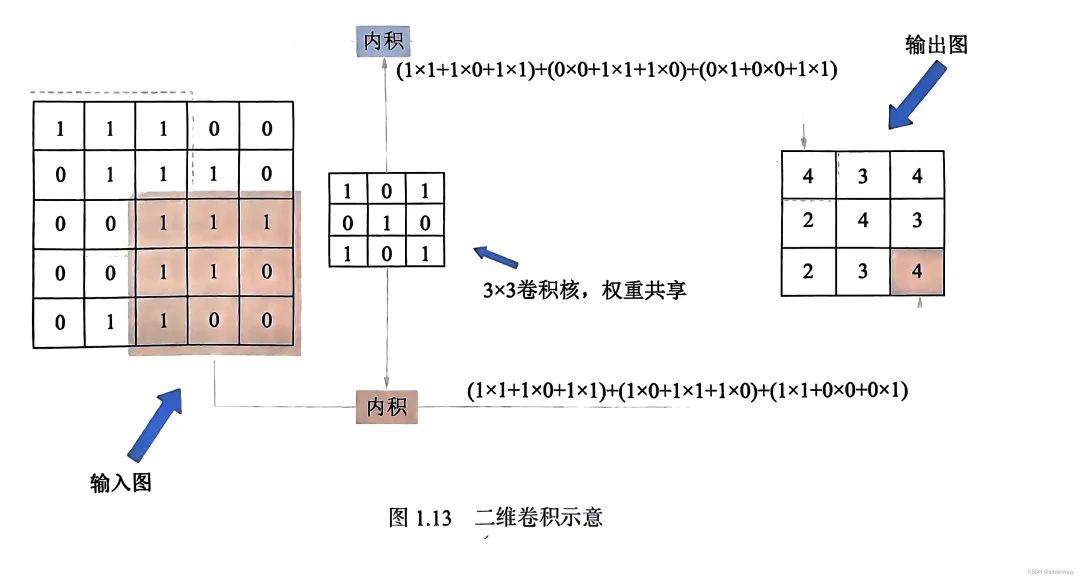
上图展示的是单个图像的卷积,而一个卷积神经网络,其每一层都是由多个图组成的,将其成为特征图或者特征平面,如下图所示。
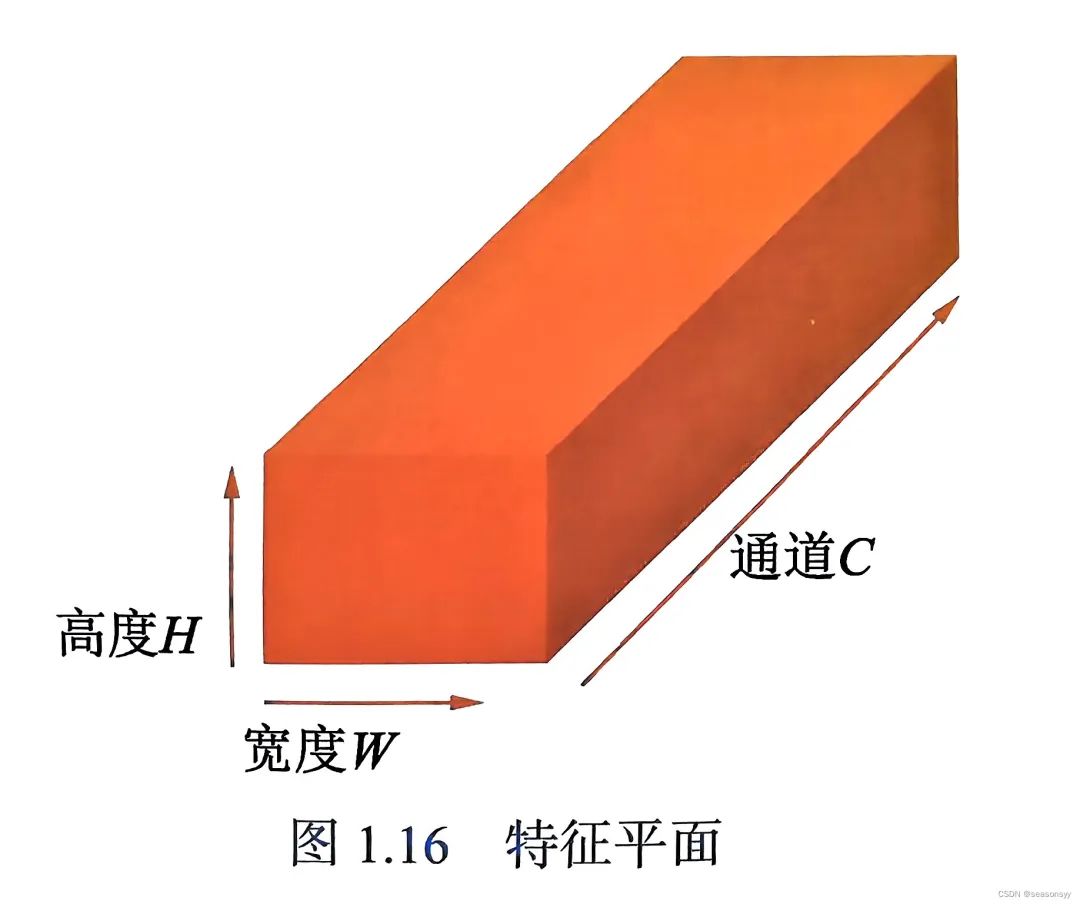
特征平面(Frature Map)包含高度、宽度和通道共三个维度,形状为C×H×W。
多通道卷积
在卷积神经网络中,要实现的是多通道卷积,假设输入特征图大小是Ci×Hi×Wi,输出特征图大小是C0×H0×W0,多通道卷积如下图所示。
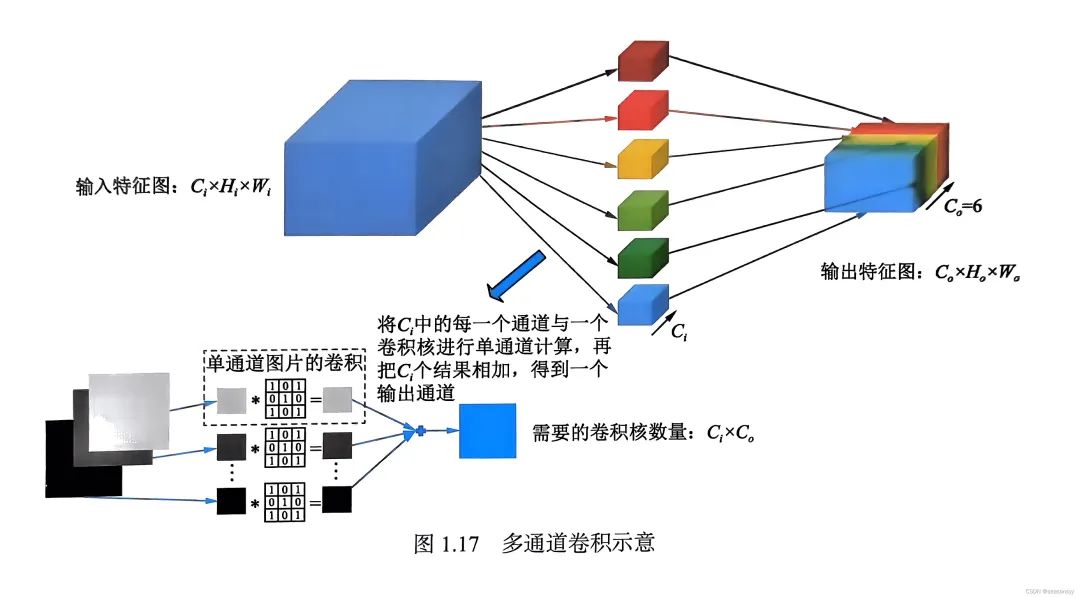
其中,每个输出特征图都由Ci个卷积核与通道数为Ci 的输入特征图进行逐通道卷积,然后将结果相加,一共需要Ci×C0个卷积核,每Ci 个为一组,共C0组。
3.权重共享
当对每组进行卷积时,不同的通道使用不同的卷积核。但当卷积核在同一幅图的不同空间位置进行卷积时,采取的是权重共享的模式,这是卷积神经网络非常重要的概念。
-
局部连接:思想来自生理学的感受野机制和图像的局部统计特性
-
权重共享:可以使得图像在一个局部区域学习到的信息应用到其他区域,使同样的目标在不同的位置能够提取到同样的特征。
局部连接和权重共享结构大大降低了参数量。
√卷积神经网络某一层的参数量由输入通道数N、输出通道数M和卷积核的大小r决定。
√一层连接的参数量=N×M×r×r
4.感受野
感受野可以将感受野理解为视觉感受区域的大小。在卷积神经网络中,感受野是特征平面上的一个点(即神经元)在输入图上对应的区域。
如果一个神经元的大小受到输入层N×N的神经元区域的影响,那么可以说该神经元的感受野是N×N,因为它反映了N×N区域的信息。
上图中,Conv2中的像素点为5,是由Conv1的2×2的区域得来的,而该2×2区域是由原始图像的5×5区域计算而来,因此该像素的感受野是5×5。可以看出,感受野越大,得到的全局信息就越多。
池化 05
-
图1.18中,从原图到Conv1再到Conv2,图像越来越小,每过一级项相当于一次降采样,这就是池化。
-
池化通过步长不为1的卷积来实现,也可以通过插值采样实现,本质上没有区别,只是权重不同。
池化作用:
- 池化层可以对输入的特征图进行压缩,一方面使特征图变小,简化网络计算的复杂度。PS:池化操作会使特征图缩小,有可能影响网络的准确度,对此可以通过增加特征图的深度来弥补精度的缺失
- 另一方面可以提取主要特征,有利于降低过拟合风险池化层在一定程度上保持尺度不变形。eg:一辆车图像缩小了50%后仍然能认出这是一辆车,说明处理后的图像仍然包含原始图像的最重要的特征。图像压缩时去掉的只是一些冗余信息,留下的信息则是具有尺度不变性的特征,其最能表达图像的特征。
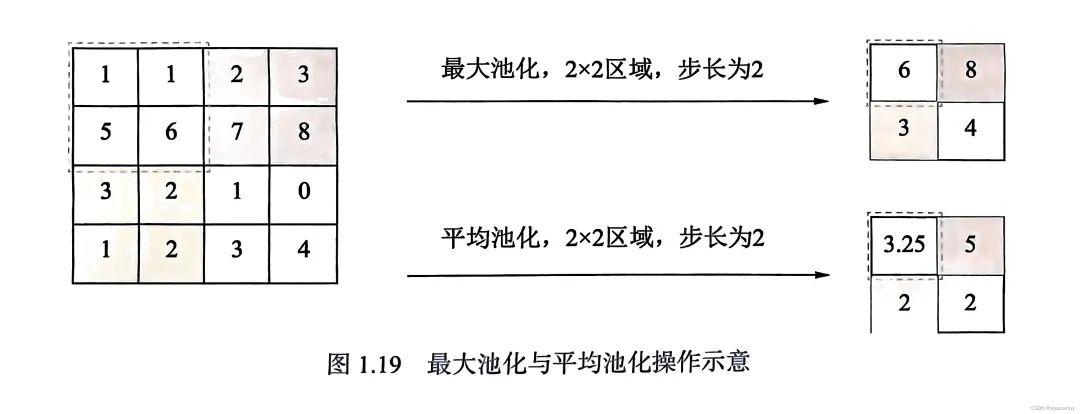
-
平均池化:计算池化区域所有元素的平均值作为该区域池化后的值,能够保留整体数据的特征,能较好的突出背景信息。
-
最大池化:池化区域的最大值作为该区域池化后的值,能更好地保留纹理特征。
套用卷积通用公式:
output=[(input-filterSize+2*padding)/stride]+1
PS:公式是向下取整
最后:
小编会不定期发布相关设计内容包括但不限于如下内容:信号处理、通信仿真、算法设计、matlab appdesigner,gui设计、simulink仿真......希望能帮到你!