【基于R语言群体遗传学】-2-模拟基因型（simulating genotypes）

书接上文，我们昨天讨论了遗传的哈代温伯格比例：

接下来，如果我们能够模拟一个过程并观察模拟结果与我们预期的是否相符，这通常有助于指导我们对这个过程的直观感觉。让我们来模拟哈代-温伯格基因型比例。首先，我们将创建一个等位基因列表，用于组成一个种群。

R 复制代码

allele <- c(rep("A",2), rep("a",8))
allele

接下来，我们创建一个矩阵来记录种群中个体的等位基因。我们从一个变量popsize开始，最初设置为100，稍后我们可以轻松地更改它以模拟不同的人口规模。然后，我们使用matrix()函数创建一个100行（由nrow = popsize定义）和两列（ncol = 2，二倍体）的矩阵，并将其保存为pop。

R 复制代码

popsize <- 100
pop <- matrix(nrow=popsize, ncol=2)

每一行对应一个个体 ，两列代表每个位点的两个副本，我们将在其中记录该个体的等位基因。现在，我们将使用R的内置sample函数随机选择等位基因来构成我们的个体基因型。

R 复制代码

for(i in 1:popsize){
  pop[i,1] <- sample(allele,1)
  pop[i,2] <- sample(allele,1)
}
pop

我们得到一个不是特别规范的100个个体的基因型随机数据模拟，里面有杂合及纯合。

我们通过循环得到A和a的计数，并计算A的frequency和a的frequency

R 复制代码

#A frequency
Acount <- 0
for(i in 1:popsize){
  if(pop[i,1]=="A"){
    Acount <- Acount+1
  }
  if(pop[i,2]=="A"){
    Acount <- Acount+1
  }
}
AFreq <- Acount/(popsize*2)

我们计算得到A的frequency为0.375，大家可能有所不同，但是都会在这附近。现在，我们将通过再次遍历矩阵并计算杂合子出现的频率以及A/A纯合子出现的频率来计算基因型频率。

R 复制代码

Hcount <- 0
AAcount <- 0
for(i in 1:popsize){
  if(pop[i,1]=="A"){
    if(pop[i,2]=="a"){
      Hcount <- Hcount+1
    }else{
      AAcount <- AAcount+1
    }
  }
  if(pop[i,1]=="a"){
    if(pop[i,2]=="A"){
      Hcount <- Hcount+1
    }
  }
}
HetFreq <- Hcount/(popsize)
AAFreq <- AAcount/(popsize)
print(c(AFreq, HetFreq, AAFreq))

现在，让我们将这些模拟的频率与所有三种基因型（A/A、A/a和a/a）的p^2、2p(1-p)和(1-p)^2预测一起绘制出来。以下命令将使用plot()函数绘制这些点。并添加曲线进行拟合：

R 复制代码

# 绘制第一个图形
plot(AFreq, HetFreq, xlab="allele frequency", ylab="",
     ylim=c(0, 1), xlim=c(0, 1), col="blue")

# 在同一个图形上添加第二个图形，不覆盖第一个图形
par(new=TRUE)
plot(AFreq, AAFreq, xlab="", ylab="", ylim=c(0, 1), xlim=c(0, 1), col="green")

# 在同一个图形上添加第三个图形，不覆盖前两个图形
par(new=TRUE)
plot(AFreq, 1-AAFreq-HetFreq, xlab="",
     ylab="genotype frequency", ylim=c(0, 1), xlim=c(0, 1),
     col="red")

# 设置点的样式，使其变大并实心
points(AFreq, HetFreq, pch=16, cex=2, col="blue") # 蓝色实心点
points(AFreq, AAFreq, pch=16, cex=2, col="green") # 绿色实心点
points(AFreq, 1-AAFreq-HetFreq, pch=16, cex=2, col="red") # 红色实心点

# 在同一个图形上添加三条曲线
curve(2*x*(1-x), 0, 1, add=TRUE, ylab=NULL, lwd=2, ylim=c(0, 1), col="darkblue")
curve(x**2, 0, 1, add=TRUE, ylab=NULL, lwd=2, ylim=c(0, 1), col="darkgreen")
curve((1-x)**2, 0, 1, add=TRUE, ylab=NULL, lwd=2, ylim=c(0, 1), col="darkred")

# 添加文本标签
text(0.5, 0.7, "Aa", col = "blue")
text(0.9, 0.7, "AA", col = "green")
text(0.1, 0.7, "aa", col = "red")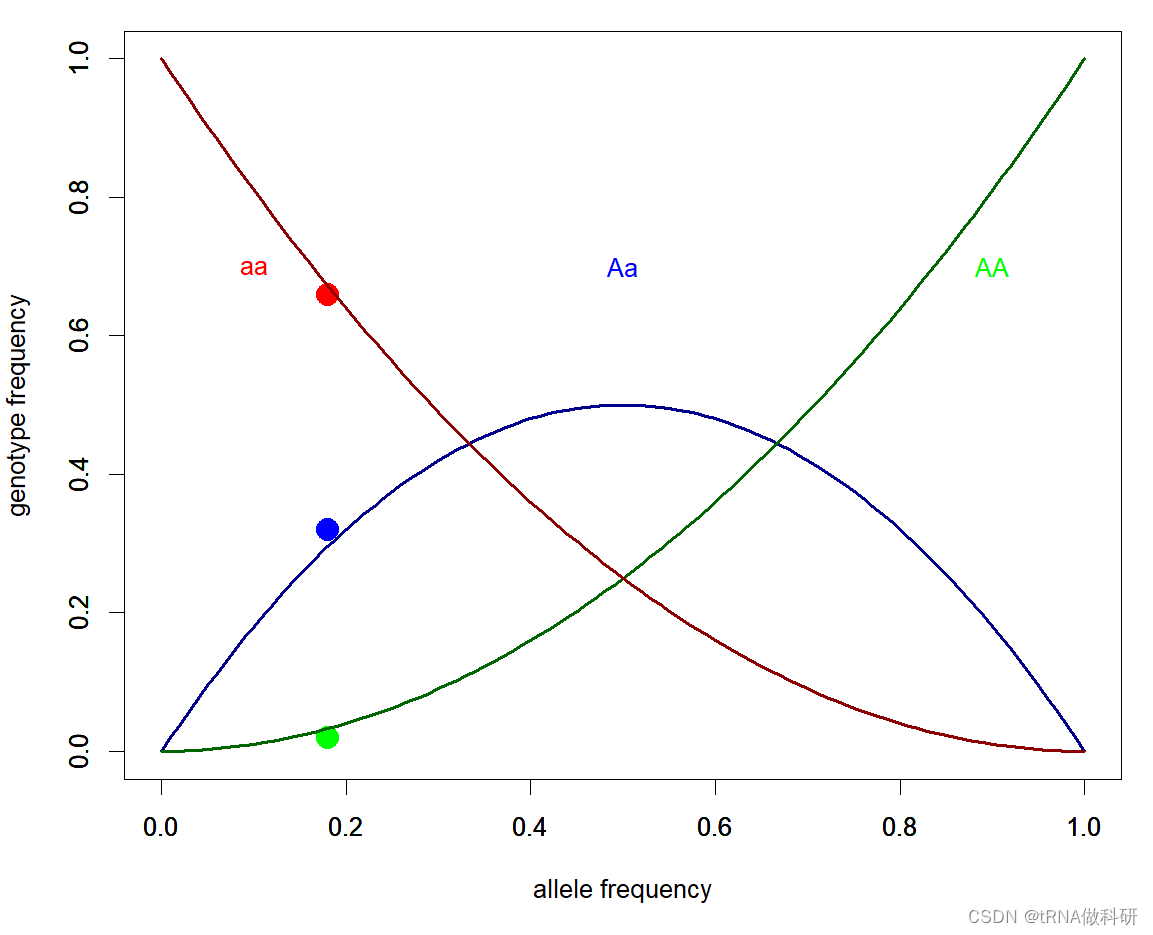

我们通常对许多点的分布感兴趣。让我们修改代码，让它运行一些重复实验并同时绘制它们。每次我们运行模拟时，我们都会抽取一个新的等位基因频率，因此我们运行的重复实验次数越多，我们将看到的等位基因频率范围就越广。

R 复制代码

AFreq <- numeric()
HetFreq <- numeric()
AAFreq <- numeric()
replicates <- 10
for (j in 1:replicates) {
  # Randomly sample alleles for each individual
  pop[, 1:2] <- t(replicate(popsize, sample(allele, 2)))
  
  # Count the number of 'A' alleles
  Acount <- sum(pop == "A")
  
  # Calculate the frequency of 'A' alleles
  AFreq[j] <- Acount / (popsize * 2)
  
  # Count the number of heterozygotes and AA homozygotes
  genotypes <- apply(pop, 1, function(ind) {
    if (all(ind == "A")) {
      "AA"
    } else if (any(ind == "A")) {
      "Het"
    } else {
      "aa"
    }
  })
  
  # Calculate the frequencies of heterozygotes and AA homozygotes
  HetFreq[j] <- sum(genotypes == "Het") / popsize
  AAFreq[j] <- sum(genotypes == "AA") / popsize
}

我们如此得到一系列点，然后进行可视化：

R 复制代码

plot(AFreq, HetFreq, xlab="allele frequency",ylab = "",
     ylim=c(0, 1), xlim=c(0, 1), col="blue")
par(new=TRUE)
plot(AFreq, AAFreq,  xlab="", ylab = "", ylim=c(0, 1), xlim=c(0, 1), col="green")
par(new=TRUE)
plot(AFreq, 1-AAFreq-HetFreq,xlab = "",
     ylab="genotype frequency", ylim=c(0, 1), xlim=c(0, 1),
     col="red")
# 绘制第一个图形
plot(AFreq, HetFreq, xlab="allele frequency", ylab="",
     ylim=c(0, 1), xlim=c(0, 1), col="blue")

# 在同一个图形上添加第二个图形，不覆盖第一个图形
par(new=TRUE)
plot(AFreq, AAFreq, xlab="", ylab="", ylim=c(0, 1), xlim=c(0, 1), col="green")

# 在同一个图形上添加第三个图形，不覆盖前两个图形
par(new=TRUE)
plot(AFreq, 1-AAFreq-HetFreq, xlab="",
     ylab="genotype frequency", ylim=c(0, 1), xlim=c(0, 1),
     col="red")

# 在同一个图形上添加三条曲线
curve(2*x*(1-x), 0, 1, add=TRUE, ylab=NULL, lwd=2, ylim=c(0, 1), col="darkblue")
curve(x**2, 0, 1, add=TRUE, ylab=NULL, lwd=2, ylim=c(0, 1), col="darkgreen")
curve((1-x)**2, 0, 1, add=TRUE, ylab=NULL, lwd=2, ylim=c(0, 1), col="darkred")

# 添加文本标签
text(0.5, 0.7, "Aa", col = "blue")
text(0.9, 0.7, "AA", col = "green")
text(0.1, 0.7, "aa", col = "red")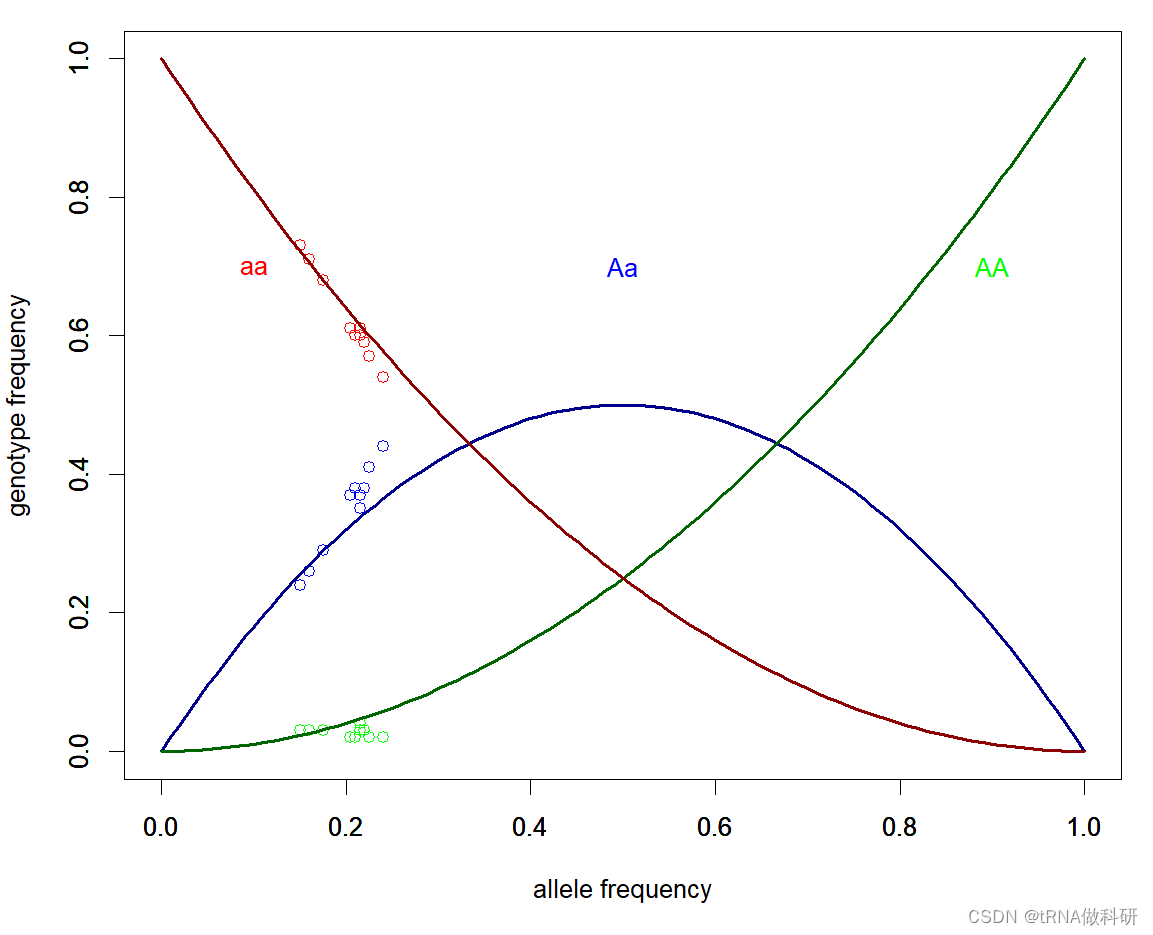

目前为止，这些模拟是通过从原始的"等位基因"列表（总共十个中有两个"A"）中以p = 0.2为中心抽样等位基因频率来运行的。然而，我们可以修改代码，使其在整个可能的等位基因频率范围内运行。我们使用runif

R 复制代码

p <- runif(1)
for(i in 1:popsize){ #Randomly sample alleles
  pop[i,1] <- sample(allele,1)
  pop[i,2] <- sample(allele,1)
}
for(i in 1:popsize){
  if(runif(1)<p){
    pop[i,1] <- "A"
  }else{
    pop[i,1] <- "a"
  }
  if(runif(1)<p){
    pop[i,2] <- "A"
  }else{
    pop[i,2] <- "a"
  }
}

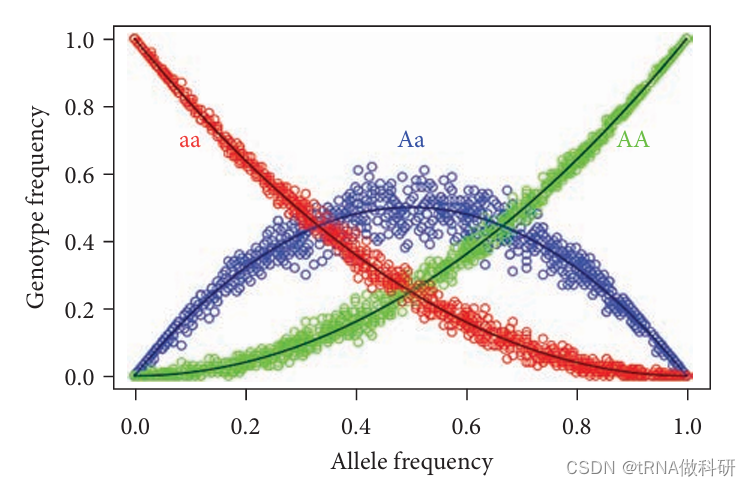
当然大家可以通过改变种群大小去看看差异

下一章将讲解R语言计算等位基因频率相关的内容，欢迎大家点赞收藏。