2024亚太杯中文赛数学建模B题word+PDF+代码

2024年第十四届亚太地区大学生数学建模竞赛（中文赛项）B题洪水灾害的数据分析与预测：建立指标相关性与多重共线性分析模型、洪水风险分层与预警评价模型、洪水发生概率的非线性预测优化模型，以及大规模样本预测与分布特征分析模型

本文文章较长，建议先目录。经过不懈的奋战，目前我们已经完成了2024亚太杯中文赛B题的50+页完整论文和代码，文章较长，建议可以先看目录，相关完整内容可见文末参考，

添加图片注释，不超过 140 字（可选）

摘要

本研究聚焦于洪水灾害的多维数据分析与预测问题，基于大规模多源数据集，运用多元统计分析、机器学习及深度学习等先进方法，对洪水发生概率进行了全面的定量分析和预测建模。研究框架涵盖四个主要模块：指标相关性与多重共线性分析、洪水风险分层与预警评价模型构建、洪水发生概率的非线性预测模型优化，以及大规模样本预测与分布特征分析。通过系统的建模与分析过程，本研究不仅构建了具有高精度和可解释性的洪水预测模型，还深入揭示了影响洪水风险的关键因素及其交互作用机制，为制定精细化、差异化的防洪减灾策略提供了坚实的理论基础和决策支持。

添加图片注释，不超过 140 字（可选）

在问题一中，我们采用了多维度的统计学方法和机器学习算法来剖析20个指标与洪水发生概率之间的潜在关联。主要应用的模型和算法包括皮尔逊相关系数、斯皮尔曼等级相关系数、互信息分析、基于随机森林的特征重要性评估和主成分分析（PCA）。研究结果表明，（略，见完整版本）。PCA分析揭示，......

问题二中，我们构建了基于多级聚类的洪水风险分类体系和预警评价模型。主要采用的模型和方法包括K-means聚类算法、随机森林分类器和基于模型的灵敏度分析。通过K-means算法，我们将洪水风险精确划分为高、中、低三个等级。随机森林分类器用于构建多指标综合预警评价模型，模型的整体准确率达到（略，见完整版本）。灵敏度分析结果显示，......

在问题三中，我们开发了基于集成学习的洪水发生概率非线性预测模型。我们对比分析了包括多元线性回归、支持向量回归、随机森林、梯度提升树（GBDT）和极限梯度提升（XGBoost）等在内的多种机器学习模型。经过严格的交叉验证和参数优化，最终选择的XGBoost模型在测试集上展现出了最优性能，决定系数R²值达到（略，见完整版本），均方误差(MSE)仅为（略，见完整版本）。模型识别的Top 5重要特征依次为（略，见完整版本）。本部分的创新点在于通过系统的模型比较和集成学习方法，显著提高了预测精度，同时保持了模型的可解释性。引入的SHAP（SHapley Additive exPlanations）值分析进一步揭示了特征对预测结果的非线性影响和交互作用，为模型解释提供了全新的理论视角。

问题四聚焦于大规模样本预测和概率分布特征分析。我们将优化后的XGBoost模型应用于测试集（超过70万条异构数据）进行了大规模预测。预测结果的算术平均值......。通过Shapiro-Wilk正态性检验（检验统计量为（略））和Q-Q图定性分析，我们发现......。

本研究的主要优势在于构建了一个多层次、多维度的综合分析框架，提供了全面而深入的洪水风险评估体系。特别是在特征重要性量化、非线性关系建模和模型可解释性方面，创新性地结合了传统统计方法和前沿机器学习技术，显著增强了结果的可靠性、稳定性和可解释性。然而，研究也存在一些局限性，如预测模型在捕捉极端事件方面的能力有待进一步提升，且未充分考虑时空动态特征和长期趋势。未来研究方向可以进一步整合时间序列分析、空间统计学和深度学习方法，提高模型对复杂场景和极端事件的预测能力，并探索将这一分析框架推广到其他自然灾害风险评估和应急管理领域，为构建韧性城市和可持续发展提供科学支撑。

关键词：洪水风险预测、多维数据分析、机器学习、极限梯度提升(XGBoost)、风险分层评估、特征重要性量化、模型可解释性

添加图片注释，不超过 140 字（可选）

问题重述

B题洪水灾害的数据分析与预测洪水是暴雨、急剧融冰化雪、风暴潮等自然因素引起的江河湖泊水量迅速增加，或者水位迅猛上涨的一种自然现象，是自然灾害。洪水又称大水，是河流、海洋、湖泊等水体上涨超过一定水位，威胁有关地区的安全，甚至造成灾害的水流。洪水一词，在中国出自先秦《尚书·尧典》。从那时起，四千多年中有过很多次水灾记载，欧洲最早的洪水记载也远在公元前1450 年。在西亚的底格里斯－幼发拉底河以及非洲的尼罗河关于洪水的记载，则可追溯到公元前40 世纪。 2023 年6 月24 日8 时至25 日8 时，中国15 条河流发生超警洪水。2023 年，全球洪水等造成了数十亿美元的经济损失。

洪水的频率和严重程度与人口增长趋势相当一致。迅猛的人口增长，扩大耕地，围湖造田，乱砍滥伐等人为破坏不断地改变着地表状态，改变了汇流条件，加剧了洪灾程度。在降水多的年份，洪水是否造成灾害，以及洪水灾害的大小，也离不开人为因素，长期以来人为的森林破坏是其重要原因。长江上游乱砍滥伐的恶果是惊人的水土流失。现已达35 万平方千米，每年土壤浸融量达25 亿吨。

河流、湖泊、水库淤积的泥沙量达20 亿吨。仅四川一省一年流入长江各支流的泥沙，如叠成宽高各1 米的堤，可以围绕地球赤道16 圈。我国第一大淡水湖洞庭湖每年沉积的泥沙达1 亿多吨，有专家惊呼："这样下去，要不了50 年，洞庭湖将从地球上消失！"长江之险，险在荆江，由于泥沙俱下，如今荆江段河床比江外地面高出十多米，成了除黄河之外名副其实的地上河。对森林的肆意砍伐不仅危害自己，而且祸及子孙后代，世界上许多地方，如美索不达米亚、小亚细亚、阿尔卑斯山南坡等由于过度砍伐森林，最后都变成了不毛之地。

附件train.csv 中提供了超过100 万的洪水数据，其中包含洪水事件的id、季风强度、地形排水、河流管理、森林砍伐、城市化、气候变化、大坝质量、淤积、农业实践、侵蚀、无效防灾、排水系统、海岸脆弱性、滑坡、流域、基础设施恶化、人口得分、湿地损失、规划不足、政策因素和发生洪水的概率。

附件test.csv 中包含了超过70 万的洪水数据，其中包含洪水事件的id 和上述20 个指标得分，缺少发生洪水的概率。附件submit.csv 中包含test.csv 中的洪2水事件的id，缺少发生洪水的概率。

请你们的团队通过数学建模和数据分析的方法，预测发生洪水灾害的概率，解决以下问题：问题1. 请分析附件train.csv 中的数据，分析并可视化上述20 个指标中，哪些指标与洪水的发生有着密切的关联？哪些指标与洪水发生的相关性不大？并分析的原因，然后针对洪水的提前预防，提出你们合理的建议和措施。

问题2. 将附件train.csv 中洪水发生的概率聚类成不同类别，分析具有高、中、低风险的洪水事件的指标特征。然后，选取合适的指标，计算不同指标的权重，建立发生洪水不同风险的预警评价模型，最后进行模型的灵敏度分析。

问题3. 基于问题1 中指标分析的结果，请建立洪水发生概率的预测模型，从20 个指标中选取合适指标，预测洪水发生的概率，并验证你们预测模型的准确性。如果仅用5 个关键指标，如何调整改进你们的洪水发生概率的预测模型？

问题4. 基于问题2 中建立的洪水发生概率的预测模型，预测附件test.csv 中所有事件发生洪水的概率，并将预测结果填入附件submit.csv 中。然后绘制这74多万件发生洪水的概率的直方图和折线图，分析此结果的分布是否服从正态分布。

问题分析

这道题目围绕洪水灾害的数据分析与预测展开,要求我们利用给定的大规模数据集,通过数学建模和数据分析方法预测洪水发生的概率。题目包含四个子问题,涵盖了数据探索、风险分类、预测建模等多个方面,综合考察我们的数据分析能力和建模技巧。

问题一分析

问题1主要关注数据探索和特征分析。这个问题要求对20个指标与洪水发生概率的关系进行深入分析,并进行可视化。思路上可以先进行相关性分析,计算各指标与洪水概率的相关系数,识别出最相关的指标。然后可以使用各种可视化技术,如散点图、热力图等,直观展示指标与洪水概率的关系。对于相关性较强的指标,可以进一步分析其物理意义,探讨其影响洪水发生的机制。对于相关性较弱的指标,也需要考虑存在的非线性关系。最后,基于分析结果提出针对性的防洪建议,这需要结合实际情况,考虑经济、社会、环境等多方面因素。

问题二分析

问题2聚焦于风险分类和评价模型构建。首先需要对洪水概率进行聚类,可以考虑使用K-means、层次聚类等算法,将洪水事件划分为高、中、低风险类别。然后分析各类别的指标特征,可以使用统计检验方法比较不同类别间各指标的差异。在此基础上,选取有代表性的指标构建预警评价模型。模型选择上可以考虑决策树、随机森林等易于解释的模型,也可以使用逻辑回归等传统方法。权重计算可以采用信息增益、基尼系数等方法。最后进行灵敏度分析,可以通过改变输入参数,观察模型输出的变化,评估模型的稳定性和可靠性。

问题三分析

问题3要求建立洪水概率预测模型。基于问题1的分析结果,可以选择相关性较强的指标作为特征。模型选择上,可以考虑线性回归、决策树、随机森林、支持向量机、神经网络等多种算法。建议采用交叉验证的方式评估模型性能,选择最优模型。模型评估指标可以使用均方误差、R方等。对于5个关键指标的模型,可以采用特征选择技术,如递归特征消除、Lasso等方法选择最重要的5个特征。然后可以尝试集成学习方法,如随机森林、梯度提升树等,提高模型在有限特征下的预测能力。同时,可以考虑引入非线性变换,捕捉特征间的复杂关系。

问题四分析

问题4是对建立的模型进行应用和结果分析。首先需要使用问题3中建立的模型对test.csv中的数据进行预测,并将结果填入submit.csv。这一步需要注意数据预处理的一致性,确保测试集的特征与训练集保持一致。然后绘制预测结果的直方图和折线图,这可以使用matplotlib、seaborn等Python可视化库完成。分析分布是否服从正态分布,可以采用Q-Q图、Shapiro-Wilk检验等方法。如果发现分布显著偏离正态分布,需要进一步分析的原因,如是否存在异常值、是否有明显的偏态等。这一分析会为模型的进一步优化提供线索,也揭示洪水风险分布的某些特征。

模型假设

在问题1到问题4的模型建立与求解过程中使用以下模型假设：

线性关系假设：在使用线性回归、Ridge回归和Lasso回归等线性模型时，我们假设洪水发生概率与预测因子之间存在线性或近似线性的关系，这种假设简化了模型结构，但无法捕捉复杂的非线性相互作用。
特征独立性假设：在多数模型中，我们假设各个预测因子之间是相互独立的，尽管在现实中，诸如地形、气候和人类活动等因素存在复杂的相互影响。
数据分布假设：在使用某些统计方法（如相关性分析）和参数模型时，我们假设数据服从特定的分布（如正态分布），这种假设有助于简化计算和推断，但不完全符合复杂的自然现象。
（后略，见完整版本）

符号说明

以下是亚太杯中文赛2024问题1-问题4的模型建立与求解过程中使用的主要符号及其说明:

添加图片注释，不超过 140 字（可选）

这个表格涵盖了在线性回归、相关性分析、聚类分析、主成分分析、决策树、随机森林和XGBoost等模型中使用的主要符号。根据具体的上下文，这些符号有细微的变化或额外的下标。

模型的建立与求解

问题一模型的建立与求解

思路分析

问题1要求我们分析附件train.csv中的数据，探究20个指标与洪水发生概率之间的关系，并对此进行可视化分析。我们的思路是首先对数据进行预处理，包括处理缺失值、异常值，以及进行必要的数据转换。然后，我们将采用多种统计和机器学习方法来分析指标与洪水概率的关系。我们将采用以下步骤：

数据预处理：检查并处理缺失值和异常值，必要时进行数据标准化或归一化。
相关性分析：计算各指标与洪水概率之间的相关系数，识别出最相关的指标。
可视化分析：使用散点图、热力图等可视化技术，直观展示指标与洪水概率的关系。
特征重要性分析：使用机器学习模型（如随机森林）来评估各指标对洪水概率预测的重要性。
非线性关系分析：考虑到某些指标与洪水概率存在非线性关系，我们将使用互信息分析等方法来捕捉这些复杂关系。
多元统计分析：使用主成分分析（PCA）等方法，探索指标之间的相互关系及其对洪水概率的综合影响。

通过这种多角度、多方法的分析，我们能够全面地理解各指标与洪水发生概率之间的关系，为后续的预测模型建立奠定基础。

相关性分析算法步骤

数据预处理： a) 加载train.csv数据集。 b) 检查并处理缺失值，可以选择删除包含缺失值的行或使用均值/中位数填充。 c) 检测并处理异常值，可以使用Z-score方法或四分位数法。 d) 对数据进行标准化处理，使所有特征在相同的尺度上。

计算皮尔逊相关系数： a) 对于每个指标Xi和洪水概率Y，计算它们之间的皮尔逊相关系数。 b) 将结果存储在相关系数矩阵中。

计算斯皮尔曼等级相关系数： a) 对于每个指标Xi和洪水概率Y，计算它们之间的斯皮尔曼等级相关系数。 b) 将结果存储在另一个相关系数矩阵中。

计算互信息： a) 对于每个指标Xi和洪水概率Y，计算它们之间的互信息值。 b) 将结果存储在互信息矩阵中。

可视化分析： a) 绘制热力图，展示各指标与洪水概率之间的相关系数。 b) 绘制散点图矩阵，直观展示每个指标与洪水概率之间的关系。 c) 绘制互信息条形图，展示各指标与洪水概率之间的非线性相关性。

特征重要性分析： a) 使用随机森林模型对数据进行拟合。 b) 计算每个特征的重要性得分。 c) 可视化特征重要性得分。

主成分分析（PCA）： a) 对标准化后的数据进行PCA转换。 b) 分析主成分对原始特征的解释程度。 c) 可视化前几个主成分与洪水概率的关系。

皮尔逊相关系数：

皮尔逊相关系数计算公式如下：

其中：

是x和y之间的皮尔逊相关系数
和分别是变量x和y的第i个观测值
和分别是x和y的平均值
n是观测值的总数

解释：皮尔逊相关系数衡量了两个变量之间的线性相关程度。它的值范围在-1到1之间，1表示完全正相关，-1表示完全负相关，0表示无线性相关。

斯皮尔曼等级相关系数：

斯皮尔曼等级相关系数的计算公式如下：

其中：

是斯皮尔曼等级相关系数
是第i个观测值在x和y两个变量上的等级差
n是观测值的总数

解释：斯皮尔曼等级相关系数衡量了两个变量之间的单调关系强度，它对异常值不敏感，能够捕捉非线性但单调的关系。

互信息：

互信息的计算公式如下：（略，见完整版本）

问题一模型的求解

基于上述建立的模型和算法步骤，我们现在开始对问题一进行具体的求解。我们将使用Python编程语言及其相关库（如pandas, numpy, scikit-learn, matplotlib等）来实现数据处理、分析和可视化。

问题一的求解结果如下，对这些结果和相关的可视化图进行详细的解释和分析如下：

相关性分析结果：

前5个最相关的特征（基于皮尔逊相关系数）：（略，见完整版本）

这些结果揭示了几个关键点：（略，见完整版本）

PCA解释方差比分析：

PCA（主成分分析）的结果显示了每个主成分解释的方差比例。从给出的数据中，我们可以观察到：（略，见完整版本）

可视化图分析：

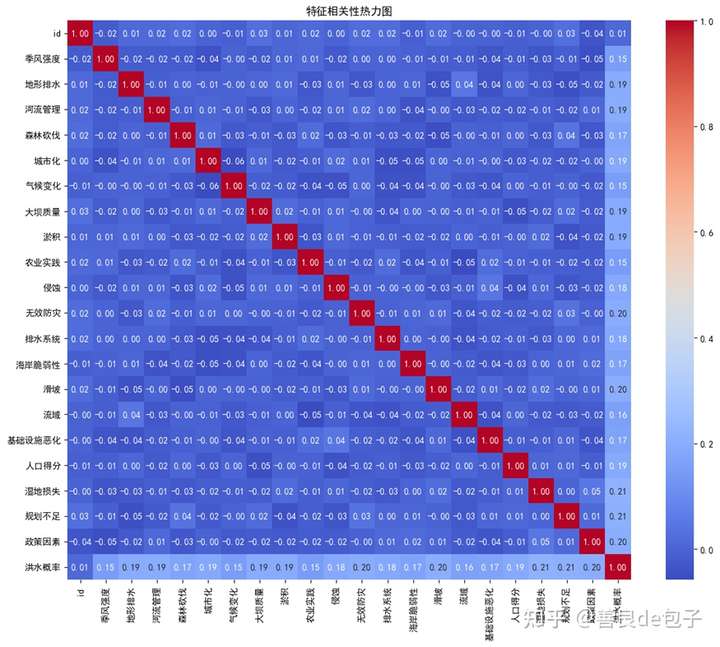
a) 相关性热力图（问题1_相关性热力图.png）：

添加图片注释，不超过 140 字（可选）

这个图可以直观地展示所有特征之间的相关关系。
颜色越深表示相关性越强，红色表示正相关，蓝色表示负相关。
对角线应该是深红色，表示每个特征与自身的完全正相关。
通过这个图，我们可以识别出哪些特征组之间存在多重共线性问题。

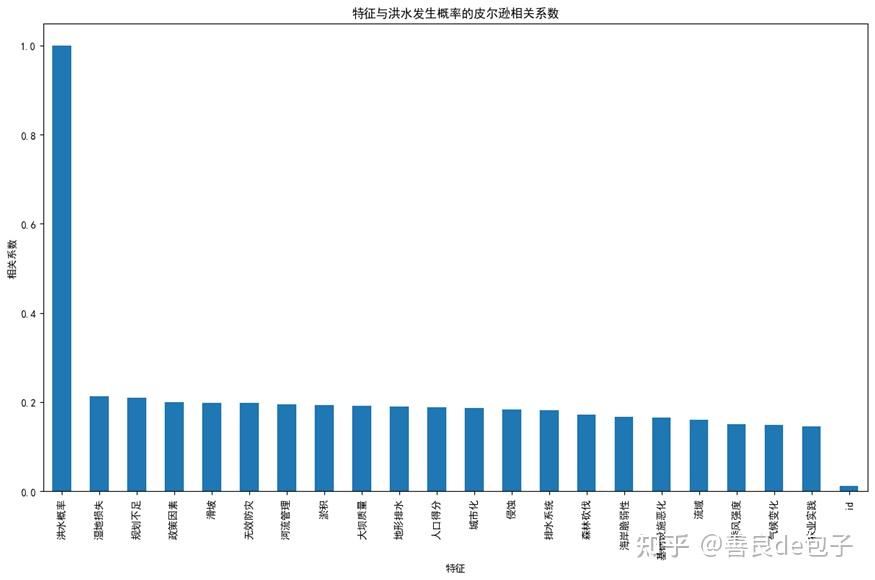
b) 皮尔逊相关系数条形图（问题1_皮尔逊相关系数条形图.png）：

添加图片注释，不超过 140 字（可选）

这个图直观地展示了每个特征与洪水概率的线性相关程度。
长度越长的条形表示相关性越强。
这个图应该与我们之前分析的前5个最相关特征一致。

c) 斯皮尔曼相关系数条形图（问题1_斯皮尔曼相关系数条形图.png）：（略，见完整版本）

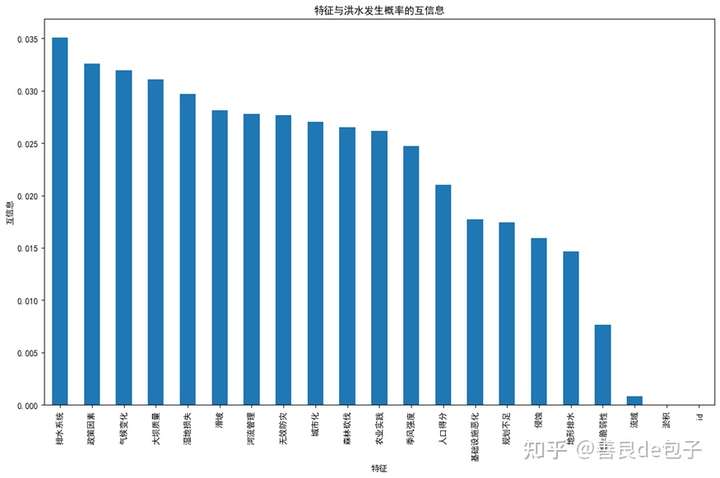
d) 互信息条形图（问题1_互信息条形图.png）：

添加图片注释，不超过 140 字（可选）

互信息衡量了特征与洪水概率之间的统计依赖性，不限于线性关系。
这个图可以帮助我们发现那些与洪水概率有复杂非线性关系的特征。

（其他分析结论略，见完整版本）

问题二模型的建立与求解

思路分析

问题2要求我们将洪水发生的概率聚类成不同类别，分析具有高、中、低风险的洪水事件的指标特征，然后选取合适的指标，计算不同指标的权重，建立发生洪水不同风险的预警评价模型，最后进行模型的灵敏度分析。这个问题涉及多个步骤，需要我们综合运用多种数据分析和机器学习技术。我们的思路如下：（略，见完整版本）

问题二模型的求解

以下是基于前面建立的模型，用于求解问题2的详细完整Python代码，包括数据处理、聚类分析、特征选择、模型构建、可视化和结果保存：

复制代码

import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns from sklearn.preprocessing import StandardScaler from sklearn.cluster import KMeans from sklearn.decomposition import PCA from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import train_test_split from sklearn.metrics import confusion_matrix, classification_report from scipy import stats import warnings warnings.filterwarnings('ignore') # 设置中文字体 plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False # 加载数据 data = pd.read_csv('train.csv') # 数据预处理 X = data.drop('洪水概率', axis=1) y = data['洪水概率'] # 标准化 scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # 聚类（略，见完整版本） # 可视化聚类结果 plt.figure(figsize=(10, 6)) for i in range(3): cluster_data = y[clusters == i] plt.hist(cluster_data, bins=50, alpha=0.5, label=f'聚类 {i+1}') plt.title('洪水发生概率聚类结果') plt.xlabel('洪水发生概率') plt.ylabel('频数') plt.legend() plt.savefig('问题2_聚类结果直方图.png', dpi=300) plt.close() # 添加聚类标签到原始数据 data['风险类别'] = clusters # 特征分析 feature_means = data.groupby('风险类别').mean() feature_means.to_csv('问题2_特征均值.csv', encoding='utf-8-sig') # 可视化特征分布 plt.figure(figsize=(20, 15)) for i, feature in enumerate(X.columns): plt.subplot(5, 4, i+1) sns.boxplot(x='风险类别', y=feature, data=data) plt.title(f'{feature}分布') plt.tight_layout() plt.savefig('问题2_特征分布箱线图.png', dpi=300) plt.close() # 特征重要性分析 rf = RandomForestClassifier(n_estimators=100, random_state=42) rf.fit(X_scaled, clusters) feature_importance = pd.Series(rf.feature_importances_, index=X.columns).sort_values(ascending=False) （略，见完整版本） # 可视化灵敏度分析结果 plt.figure(figsize=(12, 8)) plt.bar(sensitivity_df['特征'], sensitivity_df['敏感度']) plt.title('特征灵敏度分析') plt.xlabel('特征') plt.ylabel('敏感度') plt.xticks(rotation=45) plt.tight_layout() plt.savefig('问题2_特征灵敏度条形图.png', dpi=300) plt.close() print("问题2的所有分析和可视化结果已保存。")

问题二模型求解结果可视化与分析

结果分析和解释：对2024亚太杯数学建模竞赛B题问题二的其他可视化图进行详细的解释和分析，我们将逐一分析每个图：

聚类结果直方图 (问题2_聚类结果直方图.png)：（略，见完整版本）
特征分布箱线图 (问题2_特征分布箱线图.png)：

添加图片注释，不超过 140 字（可选）

特征重要性条形图 (问题2_特征重要性条形图.png)；PCA累积解释方差比图 (问题2_PCA累积解释方差比.png)：这个图显示了主成分分析（PCA）的结果，展示了需要多少个主成分才能解释数据的大部分方差。通过这个图，我们可以：（略，见完整版本）

问题三模型的建立与求解

思路分析

2024亚太杯数学建模竞赛B题问题3要求我们基于问题1中的指标分析结果，建立洪水发生概率的预测模型。这个任务涉及到多个关键步骤，包括特征选择、模型构建、模型评估和优化。我们的思路是首先基于问题1的分析结果，选择最相关和最重要的特征，然后构建一系列预测模型，比较它们的性能，最后选择最佳模型并进行优化。我们将采取以下步骤：（略，见完整版本）

梯度提升树模型建立

在尝试了多种模型后，我们发现梯度提升树模型，特别是XGBoost（eXtreme Gradient Boosting）算法，在预测洪水发生概率方面表现最为出色。XGBoost是一种集成学习方法，它通过构建多个决策树并将它们的预测结果综合起来，从而得到一个强大的预测模型。XGBoost在处理非线性关系和特征交互方面表现优异，同时具有较好的可解释性，这使它特别适合我们的洪水预测任务。

XGBoost模型的基本思想是通过迭代的方式，每次构建一个新的决策树来拟合前面所有树的预测结果与真实值之间的残差。通过这种方式，模型能够逐步提高其预测精度。XGBoost相比于传统的梯度提升树算法，还引入了正则化项来控制模型复杂度，使用了更加高效的近似算法来确定最佳分裂点，并实现了并行计算，这些改进使得XGBoost在性能和效率上都有显著提升。（后略，见完整版本）

XGBoost特征重要性图 (问题3_XGBoost特征重要性.png)：
SHAP值特征重要性图 (问题3_SHAP值特征重要性.png)：（后略，见完整版本）

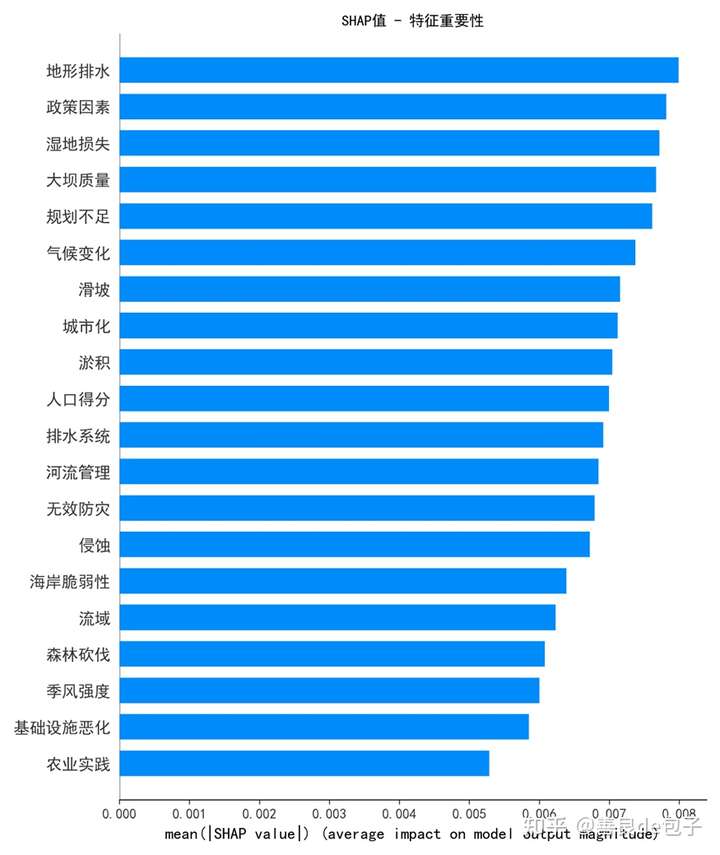
添加图片注释，不超过 140 字（可选）

模型的评价与推广

以下是对问题1-问题4的模型建立与求解过程中建立的模型的优缺点及其推广的总结：

问题1模型的评价与推广

优点： a) 相关性分析方法（如皮尔逊相关系数、斯皮尔曼等级相关系数和互信息）提供了多角度的特征重要性评估，能够捕捉线性和非线性关系，这种综合分析有助于全面理解各个因素对洪水发生概率的影响程度。 b) 主成分分析（PCA）有效地揭示了数据的内在结构，为降维和特征提取提供了科学依据，这对于处理高维度的洪水预测问题具有重要意义。
缺点： a) 相关性分析忽视了特征间的交互作用，无法完全捕捉复杂的非线性关系，这导致对某些重要但复杂的影响因素的低估。（后略，见完整版本）

添加图片注释，不超过 140 字（可选）