在现代计算机视觉领域,图像风格迁移成为一个热门话题,其中 CycleGAN(循环生成对抗网络)因其无需成对样本的特点而备受瞩目。本文将详细介绍 CycleGAN 的工作原理及其在图像风格迁移中的应用。
什么是 CycleGAN
CycleGAN 是一种生成对抗网络(GAN)的变体,用于图像到图像的转换任务。与传统的 GAN 不同,CycleGAN 能够在没有成对训练样本的情况下,将一种风格的图像转换为另一种风格。它通过两个生成器和两个判别器的协同工作,实现图像风格的互换。
CycleGAN 的架构
CycleGAN 的核心组件包括两个生成器(Generator)和两个判别器(Discriminator):
-
生成器:
- G:X→YG: X \rightarrow YG:X→Y:将来自域 XXX 的图像转换为域 YYY 的图像。
- F:Y→XF: Y \rightarrow XF:Y→X:将来自域 YYY 的图像转换为域 XXX 的图像。
-
判别器:
- DXD_XDX:判别来自域 XXX 的图像和由生成器 FFF 生成的假图像。
- DYD_YDY:判别来自域 YYY 的图像和由生成器 GGG 生成的假图像。
CycleGAN 网络本质上是由两个镜像对称的 GAN 网络组成,其结构如下图所示(图片来源于原论文):
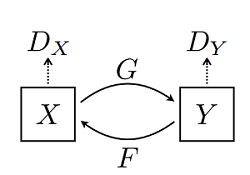
为了方便理解,这里以苹果和橘子为例介绍。上图中 𝑋𝑋 可以理解为苹果,𝑌𝑌 为橘子;𝐺𝐺 为将苹果生成橘子风格的生成器,𝐹𝐹 为将橘子生成的苹果风格的生成器,𝐷𝑋𝐷𝑋 和 𝐷𝑌𝐷𝑌 为其相应判别器,具体生成器和判别器的结构可见下文代码。模型最终能够输出两个模型的权重,分别将两种图像的风格进行彼此迁移,生成新的图像。
该模型一个很重要的部分就是损失函数,在所有损失里面循环一致损失(Cycle Consistency Loss)是最重要的。循环损失的计算过程如下图所示(图片来源于原论文):
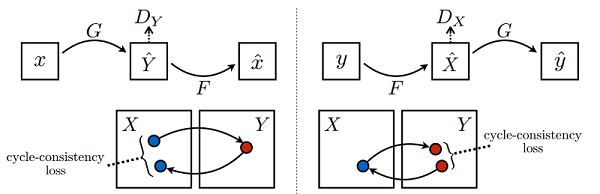
图中苹果图片 𝑥𝑥 经过生成器 𝐺𝐺 得到伪橘子 𝑌̂ 𝑌^,然后将伪橘子 𝑌̂ 𝑌^ 结果送进生成器 𝐹𝐹 又产生苹果风格的结果 𝑥̂ 𝑥^,最后将生成的苹果风格结果 𝑥̂ 𝑥^ 与原苹果图片 𝑥𝑥 一起计算出循环一致损失,反之亦然。循环损失捕捉了这样的直觉,即如果我们从一个域转换到另一个域,然后再转换回来,我们应该到达我们开始的地方。详细的训练过程见下文代码。
CycleGAN 的工作原理
对抗损失
CycleGAN 中的对抗损失与传统的 GAN 相似,生成器和判别器通过对抗训练来提高各自的能力。生成器的目标是生成逼真的图像,使判别器无法分辨真假;判别器的目标是尽可能准确地分辨真实图像和生成图像。
循环一致性损失
为了确保转换后的图像能够被逆向转换回原始图像,CycleGAN 引入了循环一致性损失。即,对于一个来自域 XXX 的图像 xxx,通过生成器 GGG 和 FFF 转换后得到的图像 F(G(x))F(G(x))F(G(x)) 应该与 xxx 尽可能接近。同样,对于一个来自域 YYY 的图像 yyy,通过生成器 FFF 和 GGG 转换后得到的图像 G(F(y))G(F(y))G(F(y)) 也应该与 yyy 尽可能接近。
对生成器 𝐺𝐺 及其判别器 𝐷𝑌𝐷𝑌 ,目标损失函数定义为:
𝐿𝐺𝐴𝑁(𝐺,𝐷𝑌,𝑋,𝑌)=𝐸𝑦−𝑝𝑑𝑎𝑡𝑎(𝑦)[𝑙𝑜𝑔𝐷𝑌(𝑦)]+𝐸𝑥−𝑝𝑑𝑎𝑡𝑎(𝑥)[𝑙𝑜𝑔(1−𝐷𝑌(𝐺(𝑥)))]𝐿𝐺𝐴𝑁(𝐺,𝐷𝑌,𝑋,𝑌)=𝐸𝑦−𝑝𝑑𝑎𝑡𝑎(𝑦)[𝑙𝑜𝑔𝐷𝑌(𝑦)]+𝐸𝑥−𝑝𝑑𝑎𝑡𝑎(𝑥)[𝑙𝑜𝑔(1−𝐷𝑌(𝐺(𝑥)))]
其中 𝐺𝐺 试图生成看起来与 𝑌𝑌 中的图像相似的图像 𝐺(𝑥)𝐺(𝑥) ,而 𝐷𝑌𝐷𝑌 的目标是区分翻译样本 𝐺(𝑥)𝐺(𝑥) 和真实样本 𝑦𝑦 ,生成器的目标是最小化这个损失函数以此来对抗判别器。即 𝑚𝑖𝑛𝐺𝑚𝑎𝑥𝐷𝑌𝐿𝐺𝐴𝑁(𝐺,𝐷𝑌,𝑋,𝑌)𝑚𝑖𝑛𝐺𝑚𝑎𝑥𝐷𝑌𝐿𝐺𝐴𝑁(𝐺,𝐷𝑌,𝑋,𝑌) 。
单独的对抗损失不能保证所学函数可以将单个输入映射到期望的输出,为了进一步减少可能的映射函数的空间,学习到的映射函数应该是周期一致的,例如对于 𝑋𝑋 的每个图像 𝑥𝑥 ,图像转换周期应能够将 𝑥𝑥 带回原始图像,可以称之为正向循环一致性,即 𝑥→𝐺(𝑥)→𝐹(𝐺(𝑥))≈𝑥𝑥→𝐺(𝑥)→𝐹(𝐺(𝑥))≈𝑥 。对于 𝑌𝑌 ,类似的 𝑥→𝐺(𝑥)→𝐹(𝐺(𝑥))≈𝑥𝑥→𝐺(𝑥)→𝐹(𝐺(𝑥))≈𝑥 。可以理解采用了一个循环一致性损失来激励这种行为。
循环一致损失函数定义如下:
𝐿𝑐𝑦𝑐(𝐺,𝐹)=𝐸𝑥−𝑝𝑑𝑎𝑡𝑎(𝑥)[‖𝐹(𝐺(𝑥))−𝑥‖1]+𝐸𝑦−𝑝𝑑𝑎𝑡𝑎(𝑦)[‖𝐺(𝐹(𝑦))−𝑦‖1]𝐿𝑐𝑦𝑐(𝐺,𝐹)=𝐸𝑥−𝑝𝑑𝑎𝑡𝑎(𝑥)[‖𝐹(𝐺(𝑥))−𝑥‖1]+𝐸𝑦−𝑝𝑑𝑎𝑡𝑎(𝑦)[‖𝐺(𝐹(𝑦))−𝑦‖1]
循环一致损失能够保证重建图像 𝐹(𝐺(𝑥))𝐹(𝐺(𝑥)) 与输入图像 𝑥𝑥 紧密匹配。
综合对抗损失和循环一致性损失,CycleGAN 的总损失函数为: L(G,F,DX,DY)=LGAN(G,DY,X,Y)+LGAN(F,DX,Y,X)+λLcyc(G,F)\mathcal{L}(G, F, D_X, D_Y) = \mathcal{L}{GAN}(G, D_Y, X, Y) + \mathcal{L}{GAN}(F, D_X, Y, X) + \lambda \mathcal{L}_{cyc}(G, F)L(G,F,DX,DY)=LGAN(G,DY,X,Y)+LGAN(F,DX,Y,X)+λLcyc(G,F)
其中,λ\lambdaλ 是一个权重因子,用于平衡对抗损失和循环一致性损失。
CycleGAN 的训练过程
CycleGAN 的训练过程可以概括为以下几个步骤:
- 初始化生成器和判别器:随机初始化两个生成器 GGG 和 FFF 以及两个判别器 DXD_XDX 和 DYD_YDY 的参数。
- 更新生成器:固定判别器的参数,最小化生成器的损失函数,包括对抗损失和循环一致性损失。
- 更新判别器:固定生成器的参数,最小化判别器的损失函数,使其能够更好地区分真实图像和生成图像。
- 循环训练:交替更新生成器和判别器的参数,直到损失函数收敛。
