摘要:
1,二叉搜索树的介绍
2,二叉搜索树的查找
3,二叉搜索树的插入
4,二叉搜索树的删除
1,二叉搜索树的介绍
二叉搜索树(Binary Search Tree,简称:BST)也叫二叉查找树,他是具有下列性质的一种二叉树:
1,若左子树不空,则左子树上所有节点的值都小于根节点的值;
2,若右子树不空,则右子树上所有节点的值都大于根节点的值;
3,任意节点的子树也都是二叉搜索树;
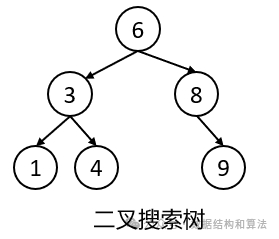
二叉搜索树有一个重要特性就是他的 中序遍历结果一定是有序的,所以它又叫二叉排序树。如上图所示,二叉搜索树的中序遍历结果是 [1,3,4,6,8,9] 。
二叉搜索树的优势在于查找,越平衡查找效率越高,时间复杂度可以达到O(logn),如果二叉搜索树退化成一个链表,时间复杂度就会达到O(n)。
为了防止二叉搜索树退化成链表,可以通过左旋和右旋让它尽可能保持平衡,这个就是我们后面要介绍的 AVL 树和红黑树。
2,二叉搜索树的查找
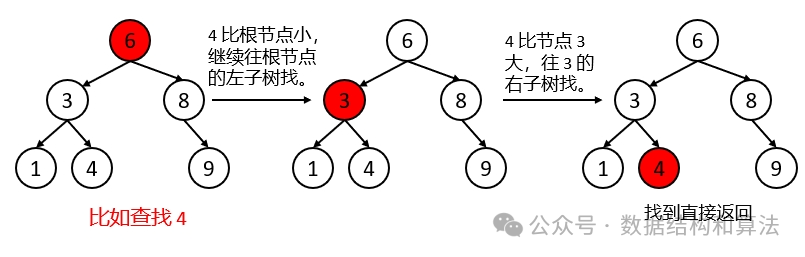
根据二叉搜索树的特性,每次只需要和当前节点比较,确定是往左边查找还是往右边查找,查找步骤如下:
1,如果当前节点为空,则查找失败。
2,否则,如果当前节点的值等于要查找的值,则查找成功。
3,否则,如果要查找的值比当前节点小,就往当前节点的左子树找。如果要查找的值比当前节点值大,就往当前节点的右子树找。