机器学习中的关键距离度量及其应用

引言

在当今的数据驱动世界中，机器学习算法扮演着至关重要的角色，它们在图像分类、面部识别、在线内容审核、零售目录优化和推荐系统等多个领域发挥着重要作用。这些算法的核心在于它们能够识别和利用数据之间的相似性。而实现这一点的关键，就在于选择合适的距离度量。

距离度量，简而言之，是一种衡量数据集中元素之间关系的方法。它通过距离函数来实现，这个函数为数据集中的每个元素提供了一种相互关系的度量。你可能好奇，这些距离函数究竟是什么，它们是如何工作的，又是如何决定数据中某个元素与另一个元素之间关系的？在本篇文章中，将深入探讨这些概念，并了解它们在机器学习中的应用。

距离函数的基本原理

顾我们在学校学习的勾股定理，它教会我们如何计算平面直角坐标系中两点之间的距离。这个定理，实际上，是欧几里得距离的基础，也是在机器学习中常用的一种距离函数。

以数据点A和B为例，可以通过计算它们在x轴和y轴上的差值，并应用勾股定理来求得它们之间的距离。

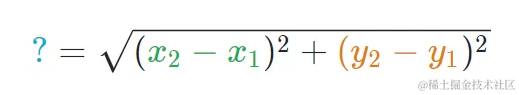
在机器学习领域，这种计算距离的方法被广泛应用。距离函数，本质上，是一种数学工具，它帮助我们量化数据集中任意两个元素之间的差异。

如果两个元素之间的距离为零，可以认为它们是等同的；
如果距离大于零，则它们有所不同；

不同的距离度量采用不同的数学公式作为其距离函数。接下来，我们将探讨这些不同的距离度量，并了解它们在机器学习建模中的作用。

常用的距离度量及其数学原理

在机器学习领域，多种距离度量被广泛使用，每一种都有其独特的数学原理和应用场景。接下来，我们将探讨一些最常见的距离度量。

闵可夫斯基距离|Minkowski Distance

闵可夫斯基距离是一种在范数向量空间中使用的度量。 它定义在满足特定条件的向量空间上，这些条件包括零向量的长度为零、标量乘法不改变向量方向以及三角不等式。这种度量因其广义性质而特别有用，可以通过调整参数p来获得不同的距离度量。

零向量 - 零向量长度为零。
标量乘法 - 向量的方向在乘以正数时不会改变，尽管其长度会改变。
三角不等式 - 如果距离是范数，那么两点之间的计算距离始终是直线。

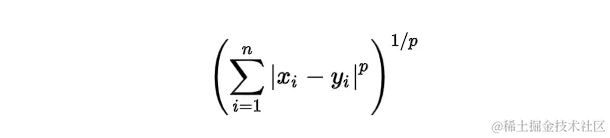
通过改变p的值，可以得到不同类型的距离：

p = 1 p = 1 p=1，得到曼哈顿距离
p = 2 p = 2 p=2，得到欧几里得距离
p = ∞ p = ∞ p=∞，得到切比雪夫距离

曼哈顿距离|Manhattan Distance

曼哈顿距离适用于需要在网格状路径中计算距离的场景，如城市街区或棋盘 。它通过将 p p p值设为1来从闵可夫斯基距离导出。

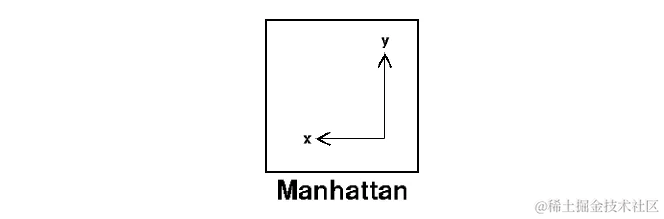
距离 d d d将使用其笛卡尔坐标的差异的绝对值之和来计算，如下所示：

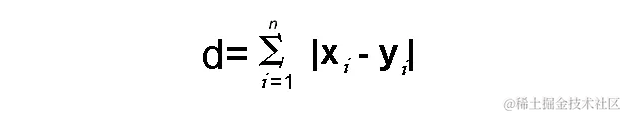
其中:

n n n：变量的数量
x i x_i xi和 y i y_i yi分别是向量x和y的变量，分别是二维向量空间，即 x = ( x 1 , x 2 , x 3 , . . . ) x = (x_1,x_2,x_3,...) x=(x1,x2,x3,...)和 y = ( y 1 , y 2 , y 3 , ... ) y = (y_1,y_2,y_3,...) y=(y1,y2,y3,...)。
距离d计算为 ( x 1 − y 1 ) + ( x 2 − y 2 ) + ( x 3 − y 3 ) + ... + ( x n − y n ) (x_1-y_1) + (x_2-y_2) + (x_3-y_3)+...+(x_n-y_n) (x1−y1)+(x2−y2)+(x3−y3)+...+(xn−yn)。

如果可视化距离计算，它看起来像下面这样：

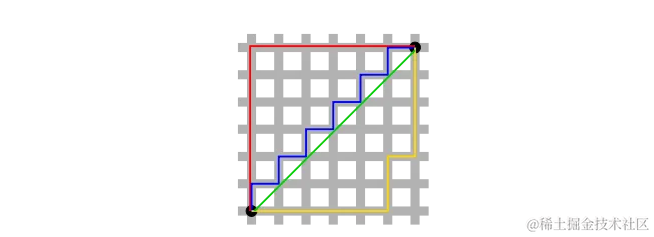
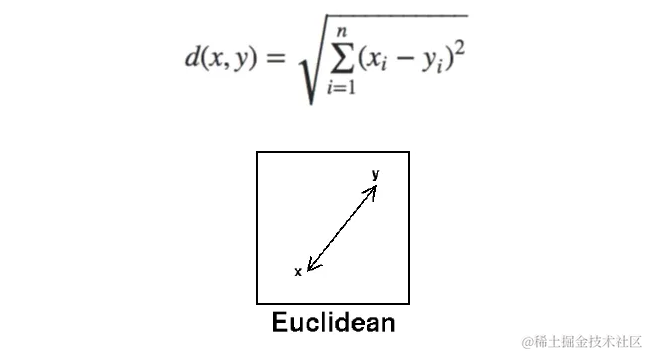
欧几里得距离|Euclidean Distance

欧几里得距离是最常用的距离度量之一，它通过将p的值设置为2来使用闵可夫斯基距离公式计算。这种距离度量在计算平面上两点间的最短路径时非常有用。

余弦距离|Cosine Distance

余弦距离主要用于衡量文档或向量之间的相似性，尤其在自然语言处理和信息检索中。它通过计算两个向量之间的角度来衡量它们的相似度。当**向量之间的大小不重要，但方向重要时，使用此特定度量。**余弦相似性公式可以从点积方程中推导出来：

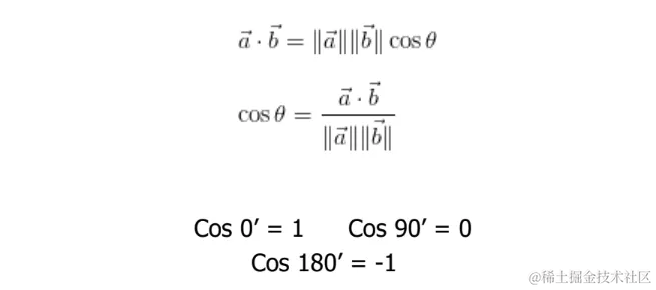
余弦值范围从-1到1，其中

1表示完全相同
-1表示完全相反
0表示正交或无关

马氏距离|Mahalanobis Distance

马氏距离用于计算多变量空间中两个数据点之间的距离。

根据维基百科的定义

马氏距离是点P和分布D之间距离的度量。测量的想法是，P距离D的平均值有多少个标准差。

使用马氏距离的好处是，它考虑了协方差，这有助于测量两个不同数据对象之间的强度/相似性。观察值与均值之间的距离可以按以下方式计算

其中 S S S是协方差度量，使用协方差的逆来获得方差归一化的距离方程。

距离度量在机器学习中的应用

在本节中，将通过具体的分类和聚类示例，探索距离度量在机器学习建模中的关键作用。将从快速介绍监督和非监督学习算法开始，然后深入探讨它们在实际应用中的使用。

分类-K-最近邻(KNN)

KNN是一种非概率监督学习算法，它通过计算数据点之间的距离来识别相似性。这种方法不需要预测数据点的概率，而是直接进行硬分类。

鸢尾花数据集示例：

以著名的鸢尾花数据集为例，该数据集包含三个类别的花卉特征。可以使用KNN算法来预测未知类别的新数据点。

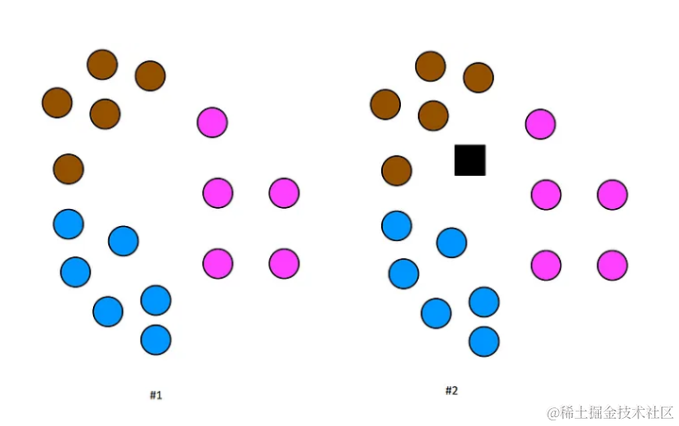
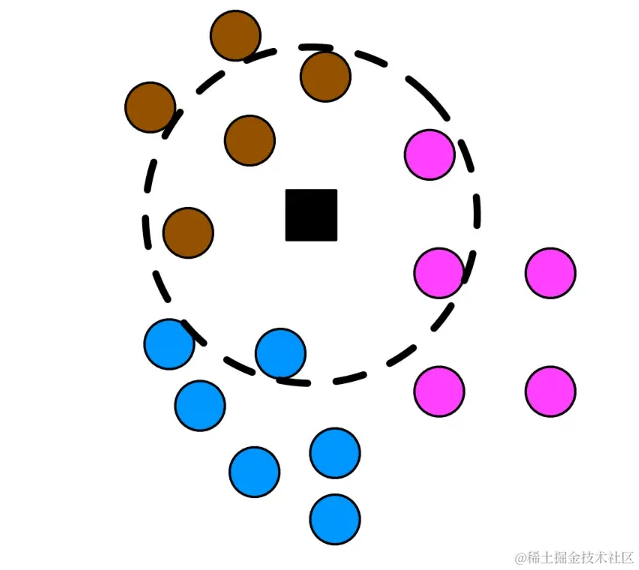
在上面的图像中，黑色正方形是一个测试数据点。现在，需要找出这个测试数据点属于哪个类别，借助KNN算法的帮助。准备数据集，创建机器学习模型，以及预测测试数据的类别。在实际应用中，通常使用scikit-learn库中的KNN分类器，它简化了模型的创建和训练过程。例如，可以使用欧几里得距离作为距离度量，这是一种在平面上计算两点间距离的简单方法。

python 复制代码

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

# 加载数据集
df = pd.read_csv('https://raw.githubusercontent.com/SharmaNatasha/Machine-Learning-using-Python/master/Datasets/IRIS.csv')
x = df.iloc[:,1:4]
y = df.iloc[:,4]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)

在KNN中，选择一个常数K，代表要考虑的最近邻的数量。然后，计算测试数据点与训练集中每个数据点的距离，并选择K个最近的数据点。这些最近邻的多数类别将成为测试数据点的预测类别。

python 复制代码

# 创建KNN模型
KNN_Classifier = KNeighborsClassifier(n_neighbors=6, p=2, metric='minkowski')

# 训练模型
KNN_Classifier.fit(x_train, y_train)

# 预测测试数据
pred_test = KNN_Classifier.predict(x_test)

在上述代码示例中，使用了闵可夫斯基距离度量，其中参数 p p p被设定为2，这实际上对应于欧几里得距离。欧几里得距离是KNN算法中最常用的距离度量，特别是在处理二维或三维数据时。

在KNN分类过程中，一旦确定了最近的邻居，就可以通过统计这些邻居中每个类别的投票数来决定测试数据点的类别。

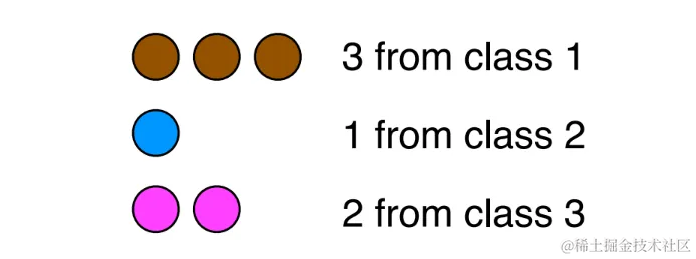
在上面的图像中，可以观察到测试数据点被正确分类为类别1，这是基于其最近的邻居中占多数的类别。

这个小例子清楚地展示了距离度量在KNN算法中的核心作用。选择合适的距离度量对于KNN分类器的性能至关重要，因为它直接影响我们找到的最近邻居的质量。不同的距离度量可能会导致不同的分类结果，因此在实际应用中，选择最合适的度量是提高模型性能的关键步骤。

聚类-K-means

在分类算法中，我们通常已知数据点的类别，这使得预测变得相对直接。然而，在聚类算法中，没有预先标记的类别信息，必须依赖数据自身的结构来发现模式。在这种情况下，距离度量成为了至关重要的工具。

K-means算法是一种无监督学习方法，它通过迭代地调整质心来将数据点分组到最近的质心所代表的聚类中。在K-means中，通常使用欧几里得距离来衡量数据点之间的相似性。

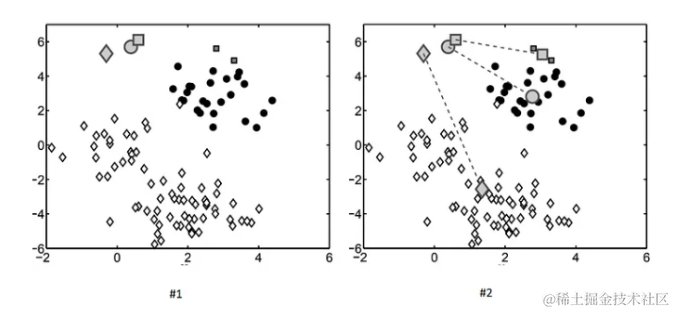
在鸢尾花数据集的例子中，首先随机选择三个质心，然后根据每个数据点与这些质心的欧几里得距离，将它们分配到最近的质心所代表的聚类中。

python 复制代码

import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt


# 加载数据集
df = pd.read_csv('https://raw.githubusercontent.com/SharmaNatasha/Machine-Learning-using-Python/master/Datasets/IRIS.csv')
x = df.iloc[:,1:4].values


# 创建KMeans模型
KMeans_Cluster = KMeans(n_clusters = 3)
y_class = KMeans_Cluster.fit_predict(x)

通过重复这个过程，直到质心的位置不再显著改变，可以得到清晰的聚类结构。

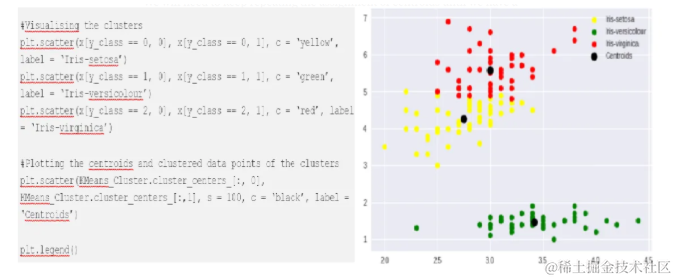
从上面的示例中可以看出，即使在没有预先标记类别的情况下，K-means算法也能够有效地将鸢尾花数据集分为三个不同的类别。这个过程展示了距离度量在发现数据内在结构中的关键作用。

自然语言处理-信息检索

在信息检索领域，我们经常处理的是未结构化的文本数据，如文章、网站、电子邮件、社交媒体帖子等。为了有效地检索这些数据，通常会使用自然语言处理（NLP）技术将文本转换为可以进行比较和分析的向量形式。

在NLP中，余弦相似度是一种常用的距离度量，它用于衡量两个向量之间的角度相似性。当向量之间的夹角越小，它们的余弦相似度越高，表示它们在语义上越相似。

为了理解余弦相似度的应用，可以通过一个简单的例子来演示：

为语料库和查询创建向量形式

python 复制代码

import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as pyplot
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.feature_extraction.text import TfidfVectorizer


vectorizer = TfidfVectorizer()
corpus = [
 'the brown fox jumped over the brown dog',
 'the quick brown fox',
 'the brown brown dog',
 'the fox ate the dog'
]

query = ["brown"]
X = vectorizer.fit_transform(corpus)
Y = vectorizer.transform(query)

在这个例子中，首先使用TfidfVectorizer将语料库中的文本转换为向量，然后对查询文本进行同样的处理。

检查相似性，即查找语料库中的哪个文档与我们的查询相关

python 复制代码

cosine_similarity(Y, X.toarray())
Results:
array([[0.54267123, 0.44181486, 0.84003859, 0.        ]])

通过计算余弦相似度，可以看到，除了第四个文档外，其他三个文档都与查询"brown"有一定的相似性。这表明这些文档中包含了查询词"brown"，而第四个文档则没有。

余弦相似度在信息检索中的应用非常广泛，特别是在搜索引擎、文本分类和情感分析等领域。它帮助我们在大量文本数据中快速找到与特定查询最相关的信息。

结论

本文深入探讨了机器学习中常用的距离和相似度度量，包括闵可夫斯基距离、曼哈顿距离、欧几里得距离、余弦距离和马氏距离。不仅了解了这些度量的数学原理，还探讨了它们在分类、聚类和信息检索等实际应用中的作用。

通过这些介绍，希望为初学者提供了一个关于距离度量在机器学习领域中应用的清晰框架，从而帮助更好地理解和应用这些概念。

参考

Cosine Similarity- Sklearn, TDS article, Wikipedia, Example
Distance_Metrics_MM
Distance Metrics- Math.net, Wiki
Minkowski Distance Metric- Wiki, Blog, Famous Metrics
importance-of-distance-metrics-in-machine-learning