现在我们知道如何创建场景图并在场景中组织对象,我们将了解如何通过技术"视锥剔除"来限制 GPU 的使用。
这种技术很容易理解。你无需将所有信息发送到 GPU,而是对可见和不可见元素进行排序,并仅渲染可见元素。借助这种技术,你将获得 GPU 计算时间。你需要知道,当信息传输到计算机中的另一个单元时,需要很长时间。例如,从 GPU 到 RAM 的信息需要时间。
如果你想像模型矩阵一样将信息从 CPU 发送到 GPU,情况也是如此。正是出于这个原因,"绘制实例"才如此强大。你将一个大块发送到 GPU,而不是一个接一个地发送元素。但这种技术不是免费的。要对元素进行排序,你需要创建一个物理场景来用数学计算一些东西。
本章将首先介绍数学概念,这将使我们了解视锥剔除的工作原理。接下来,我们将实现它。最后,我们将研究可能的优化并讨论技术的平衡。
在这个视频中,我们展示了森林中的视锥体剔除,左侧的黄色和红色形状是包含网格的边界体积。红色表示网格不可见且未发送到 GPU。黄色表示网格已渲染。如您所见,渲染了很多东西,但玩家看不到的东西很少。

NSDT工具推荐 : Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割
1、数学概念
让我们从上到下开始数学部分。首先,什么是视锥体?正如我们在维基百科中看到的,视锥体是像圆锥体或金字塔这样的固体的一部分。视锥体通常用于游戏引擎中,用来表示相机视锥体。相机视锥体表示相机的视野区域。没有限制,我们有一个金字塔,但有近处和远处,我们有一个视锥体。

如何用数学方法表示视锥体?这要归功于 6 个平面:近平面、远平面、右平面、左平面、上平面和下平面。因此,如果物体位于前方或 6 个平面上,则该物体可见。从数学上讲,平面用法线向量和到原点的距离表示。平面与四边形一样没有任何大小或限制。
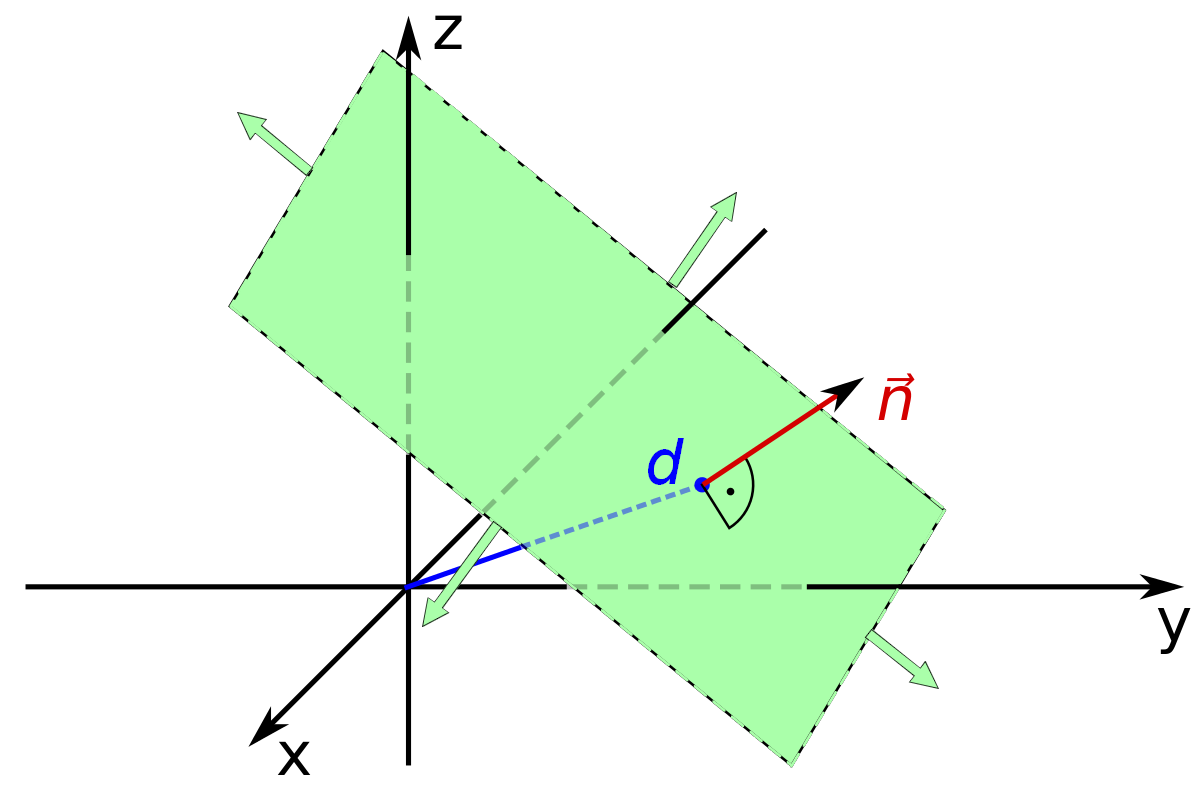
因此,创建一个结构来表示一个平面:
struct Plane
{
// unit vector
glm::vec3 normal = { 0.f, 1.f, 0.f };
// distance from origin to the nearest point in the plane
float distance = 0.f;
[...]
};我们现在可以创建视锥体 Frustrum结构:
struct Frustum
{
Plane topFace;
Plane bottomFace;
Plane rightFace;
Plane leftFace;
Plane farFace;
Plane nearFace;
};提醒:可以用一个点和一条法线构建一个平面。对于近点,法线是相机的前向量。对于远点,则相反。我们需要对右面的法线进行叉积。叉积是喜欢向量的程序员的第二个绝妙工具。它允许您获得与用两个向量创建的平面垂直的向量。为了继续,我们需要对每个向上的右轴进行叉积。我们将像这样使用它:
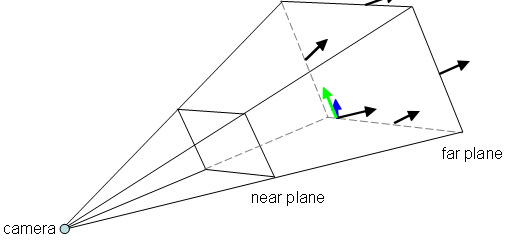
但是要知道从相机到远平面的每个向量的方向,我们需要知道远四边形的边长:
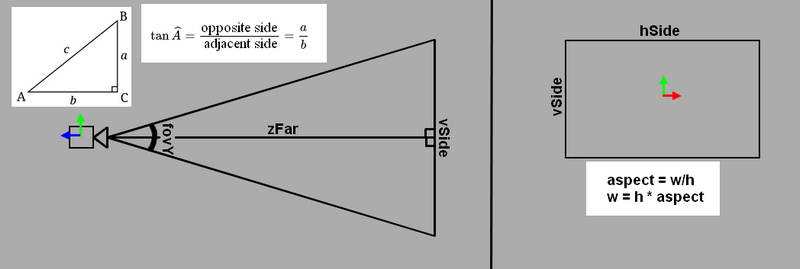
hSide 和 vSide 是受相机视锥体其他平面限制的远四边形。要计算其边缘,我们需要三角函数。如上图所示,我们有两个矩形三角形,我们可以应用三角函数。
因此,我们想要获得 vSide,它是对边,我们有 zFar,它是相机的邻边。fovY 的 tan 等于对边 (vSide) 除以邻边 (zFar)。总之,如果我将等式左侧的邻边移动,则 fovY 的 tan 乘以 zFar 等于 vSide。我们现在需要计算 hSide。由于纵横比是宽度与高度的比率,我们可以轻松获得它。因此,hSide 等于 vSide 乘以纵横比,如上图右侧所示。我们现在可以实现我们的函数:
Frustum createFrustumFromCamera(const Camera& cam, float aspect, float fovY,
float zNear, float zFar)
{
Frustum frustum;
const float halfVSide = zFar * tanf(fovY * .5f);
const float halfHSide = halfVSide * aspect;
const glm::vec3 frontMultFar = zFar * cam.Front;
frustum.nearFace = { cam.Position + zNear * cam.Front, cam.Front };
frustum.farFace = { cam.Position + frontMultFar, -cam.Front };
frustum.rightFace = { cam.Position,
glm::cross(frontMultFar - cam.Right * halfHSide, cam.Up) };
frustum.leftFace = { cam.Position,
glm::cross(cam.Up,frontMultFar + cam.Right * halfHSide) };
frustum.topFace = { cam.Position,
glm::cross(cam.Right, frontMultFar - cam.Up * halfVSide) };
frustum.bottomFace = { cam.Position,
glm::cross(frontMultFar + cam.Up * halfVSide, cam.Right) };
return frustum;
}2、包围体
让我们花一点时间来想象一个可以检测网格(一般来说,所有类型的多边形)与平面碰撞的算法。你会开始说图像是一种检查三角形是在平面上还是平面外的算法。这个算法看起来很漂亮,而且很快!
但现在想象一下,你有数百个网格,每个网格有数千个三角形。你的算法将很快标志着你的帧速率的消亡。另一种方法是将你的对象包裹在另一个具有最简单属性的几何对象中,例如球体、盒子、胶囊......现在我们的算法看起来可能不需要创建帧速率黑洞。它的形状称为包围体(bounding volume),允许我们创建比网格更简单的形状以简化流程。所有形状都有自己的属性,可以对应网格的正负。
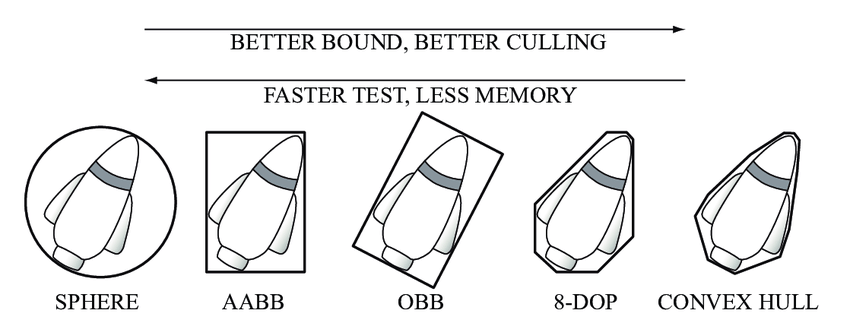
所有形状都有自己的计算复杂性。维基百科上的文章非常好,描述了一些边界体积及其平衡和应用。在本章中,我们将看到 2 个包围体:球体和 AABB。让我们创建一个简单的抽象结构 Volume 来代表我们所有的包围体:
struct Volume
{
virtual bool isOnFrustum(const Frustum& camFrustum,
const Transform& modelTransform) const = 0;
};包围球:

包围球是用来表示边界体积的最简单的形状。它由中心和半径表示。球体是封装任意旋转网格的理想选择。它必须根据物体的比例和位置进行调整。我们可以创建继承自体积结构体的结构体 Sphere:
struct Sphere : public Volume
{
glm::vec3 center{ 0.f, 0.f, 0.f };
float radius{ 0.f };
[...]
}此结构无法编译,因为我们尚未定义函数 isOnFrustum。让我们来定义它。请记住,我们的边界体积是通过网格处理的。这假设我们需要将变换应用于边界体积才能应用它。正如我们在上一章中看到的,我们将变换应用于场景图。
bool isOnFrustum(const Frustum& camFrustum, const Transform& transform) const final
{
//Get global scale is computed by doing the magnitude of
//X, Y and Z model matrix's column.
const glm::vec3 globalScale = transform.getGlobalScale();
//Get our global center with process it with the global model matrix of our transform
const glm::vec3 globalCenter{ transform.getModelMatrix() * glm::vec4(center, 1.f) };
//To wrap correctly our shape, we need the maximum scale scalar.
const float maxScale = std::max(std::max(globalScale.x, globalScale.y), globalScale.z);
//Max scale is assuming for the diameter. So, we need the half to apply it to our radius
Sphere globalSphere(globalCenter, radius * (maxScale * 0.5f));
//Check Firstly the result that have the most chance
//to faillure to avoid to call all functions.
return (globalSphere.isOnOrForwardPlane(camFrustum.leftFace) &&
globalSphere.isOnOrForwardPlane(camFrustum.rightFace) &&
globalSphere.isOnOrForwardPlane(camFrustum.farFace) &&
globalSphere.isOnOrForwardPlane(camFrustum.nearFace) &&
globalSphere.isOnOrForwardPlane(camFrustum.topFace) &&
globalSphere.isOnOrForwardPlane(camFrustum.bottomFace));
};如你所见,我们使用了一个暂时未定义的函数,名为 isOnOrForwardPlane。此实现方法称为自上而下编程,包括创建一个高级函数来确定需要实现哪种函数。它避免实现太多未使用的函数,而"自下而上"中可能会出现这种情况。因此,为了了解此函数的工作原理,让我们绘制一张图:
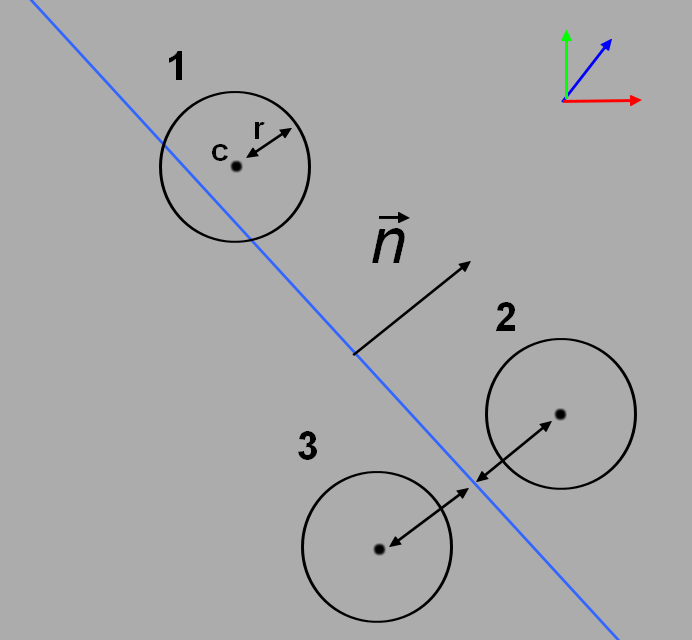
我们可以看到 3 种可能的情况:球体在平面内、在后面或前面。要检测球体是否与平面发生碰撞,我们需要计算球体中心到平面的最近距离。当我们有这个距离时,我们需要将该距离与半径进行比较。
bool isOnOrForwardPlane(const Plane& plane) const
{
return plane.getSignedDistanceToPlane(center) > -radius;
}现在我们需要在 Plane 结构中创建函数 getSignedDistanceToPlane。让我为你实现我最美丽的画作:
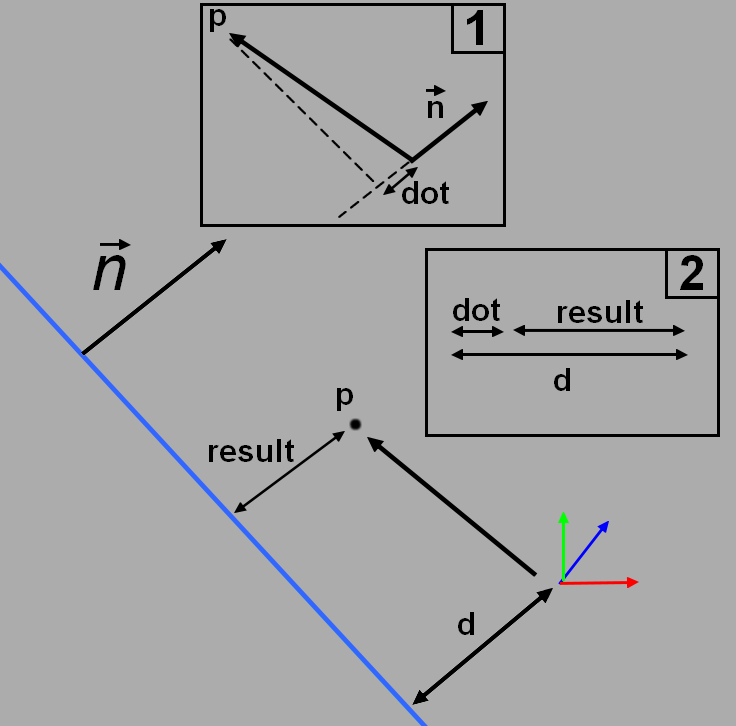
如果某点位于平面前方,则有符号距离为正距离。否则,该距离为负距离。为了获得它,我们需要调用一个朋友:点积。
点积使我们能够获得从一个向量到另一个向量的投影。点积的结果是一个比例,这个标量是一个距离。如果两个向量相反,则点积将为负。借助它,我们将获得与平面法线相同方向的向量的水平比例分量。接下来,我们需要用从平面到原点的最近距离减去这个点积。此后,你将找到此函数的实现:
float getSignedDistanceToPlane(const glm::vec3& point) const
{
return glm::dot(normal, point) - distance;
}AABB包围体

AABB 是 Axis aligned bounding box 的缩写。意思是这个体积与世界有相同的方向。它可以被构造成不同的形状,我们通常用它的中心和它的半延伸来创建它。半延伸是中心到边缘沿轴方向的距离。半延伸可以称为 Ii、Ij、Ik。在本章中,我们将其称为 Ix、Iy、Iz。

让我们用几个构造函数来创建这个结构的基础,使其创建变得最简单
struct AABB : public BoundingVolume
{
glm::vec3 center{ 0.f, 0.f, 0.f };
glm::vec3 extents{ 0.f, 0.f, 0.f };
AABB(const glm::vec3& min, const glm::vec3& max)
: BoundingVolume{},
center{ (max + min) * 0.5f },
extents{ max.x - center.x, max.y - center.y, max.z - center.z }
{}
AABB(const glm::vec3& inCenter, float iI, float iJ, float iK)
: BoundingVolume{}, center{ inCenter }, extents{ iI, iJ, iK }
{}
[...]
};我们现在需要添加函数 sOnFrustum 和 isOnOrForwardPlane。作为边界球,这个问题并不容易,因为如果我旋转网格,AABB 将需要调整。图像比文本更有说服力:

为了解决这个问题,让我们画出它:
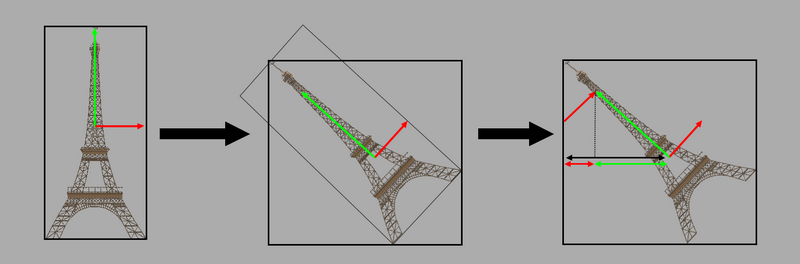
疯狂的家伙想要旋转我们美丽的埃菲尔铁塔,但我们可以看到旋转后,AABB 不再一样。为了使 Shema 更具可读性,假设 referential 不是一个单位,而是用网格的方向表示半个扩展。
为了调整它,我们可以在第三张图片中看到,新的扩展是与世界轴的点积和我们网格的缩放 referential 的总和。这个问题在 2D 中可见,但在 3D 中是同样的事情。让我们实现函数来做到这一点。
bool isOnFrustum(const Frustum& camFrustum, const Transform& transform) const final
{
//Get global scale thanks to our transform
const glm::vec3 globalCenter{ transform.getModelMatrix() * glm::vec4(center, 1.f) };
// Scaled orientation
const glm::vec3 right = transform.getRight() * extents.x;
const glm::vec3 up = transform.getUp() * extents.y;
const glm::vec3 forward = transform.getForward() * extents.z;
const float newIi = std::abs(glm::dot(glm::vec3{ 1.f, 0.f, 0.f }, right)) +
std::abs(glm::dot(glm::vec3{ 1.f, 0.f, 0.f }, up)) +
std::abs(glm::dot(glm::vec3{ 1.f, 0.f, 0.f }, forward));
const float newIj = std::abs(glm::dot(glm::vec3{ 0.f, 1.f, 0.f }, right)) +
std::abs(glm::dot(glm::vec3{ 0.f, 1.f, 0.f }, up)) +
std::abs(glm::dot(glm::vec3{ 0.f, 1.f, 0.f }, forward));
const float newIk = std::abs(glm::dot(glm::vec3{ 0.f, 0.f, 1.f }, right)) +
std::abs(glm::dot(glm::vec3{ 0.f, 0.f, 1.f }, up)) +
std::abs(glm::dot(glm::vec3{ 0.f, 0.f, 1.f }, forward));
//We not need to divise scale because it's based on the half extention of the AABB
const AABB globalAABB(globalCenter, newIi, newIj, newIk);
return (globalAABB.isOnOrForwardPlane(camFrustum.leftFace) &&
globalAABB.isOnOrForwardPlane(camFrustum.rightFace) &&
globalAABB.isOnOrForwardPlane(camFrustum.topFace) &&
globalAABB.isOnOrForwardPlane(camFrustum.bottomFace) &&
globalAABB.isOnOrForwardPlane(camFrustum.nearFace) &&
globalAABB.isOnOrForwardPlane(camFrustum.farFace));
};对于函数 isOnOrForwardPlane,我采用了我在一篇精彩文章中找到的算法。如果你想了解它的工作原理,我邀请你看一下它。我只是修改了其算法的结果以检查 AABB 是否在我的平面上或前方。
bool isOnOrForwardPlane(const Plane& plane) const
{
// Compute the projection interval radius of b onto L(t) = b.c + t * p.n
const float r = extents.x * std::abs(plane.normal.x) +
extents.y * std::abs(plane.normal.y) + extents.z * std::abs(plane.normal.z);
return -r <= plane.getSignedDistanceToPlane(center);
}要检查我们的算法是否有效,我们需要检查移动时相机前面的每个物体是否都消失了。然后,我们可以添加一个计数器,如果显示某个物体,该计数器就会递增,另一个计数器则用于控制台中显示的总数。
// in main.cpp main lopp
unsigned int total = 0, display = 0;
ourEntity.drawSelfAndChild(camFrustum, ourShader, display, total);
std::cout << "Total process in CPU : " << total;
std::cout << " / Total send to GPU : " << display << std::endl;
// In the drawSelfAndChild function of entity
void drawSelfAndChild(const Frustum& frustum, Shader& ourShader,
unsigned int& display, unsigned int& total)
{
if (boundingVolume->isOnFrustum(frustum, transform))
{
ourShader.setMat4("model", transform.getModelMatrix());
pModel->Draw(ourShader);
display++;
}
total++;
for (auto&& child : children)
{
child->drawSelfAndChild(frustum, ourShader, display, total);
}
}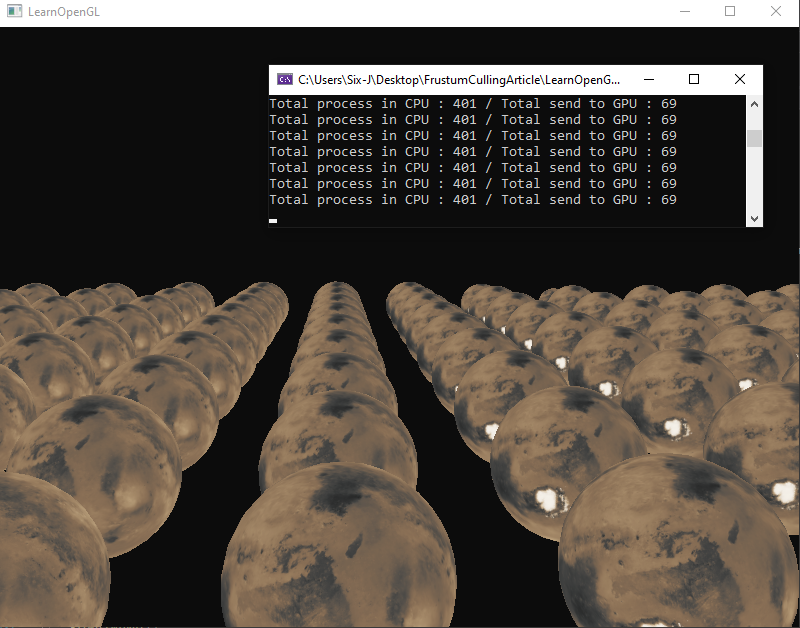
好了!发送到我们 GPU 的对象的平均数量现在约占总数的 15%,并且仅除以 6。如果您的 GPU 进程由于着色器或多边形数量而成为瓶颈,那么这是一个很棒的结果。您可以在此处找到代码。
3、优化
现在你知道如何进行视锥体剔除。视锥体剔除可用于避免计算不可见的事物。你可以使用它来不计算实体的动画状态,简化其 AI... 出于这个原因,我建议你在实体中添加 IsInFrustum 标志并执行填充此变量的视锥体剔除过程。
3.1 空间分区
在我们的示例中,视锥体剔除与 CPU 中的少量实体保持了良好的平衡。如果您想优化检测,现在需要对空间进行分区。为此,存在许多算法,每种算法都有有趣的属性,具体取决于您的使用情况:- BSH(边界球层次结构或树):存在不同种类。最简单的实现是将两个最近的物体包裹在一个球体中。用另一个组或物体等包裹这个球体...
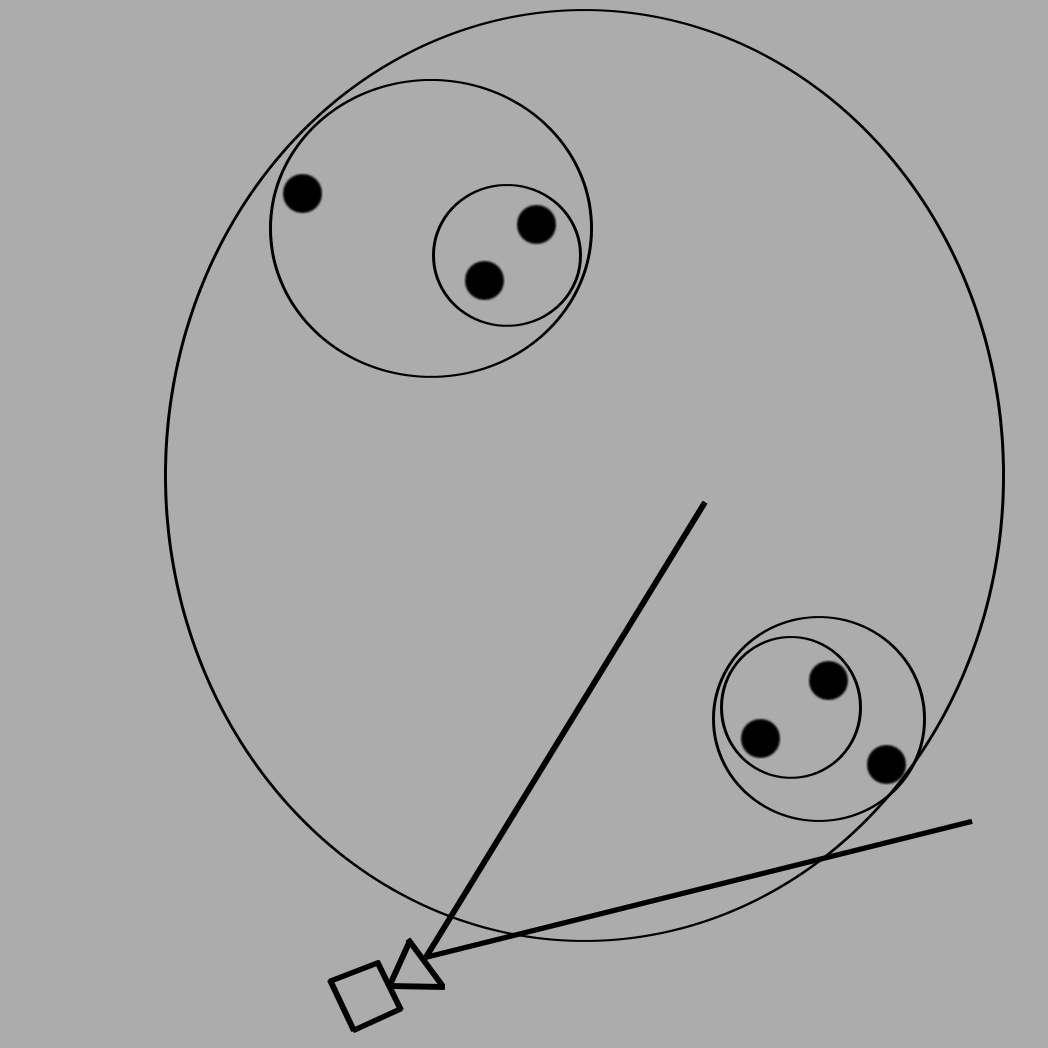
- 四叉树
主要思想是将空间分成 4 个区域,然后这些区域又可以分成 4 个区域,以此类推......直到一个对象不再被单独包裹。你的对象将成为此图的叶子。四叉树非常适合划分 2D 空间,而且如果不需要划分高度,也可以使用。它在 4x 等策略游戏中非常有用(例如帝国时代、战争选择......),因为不需要高度划分。
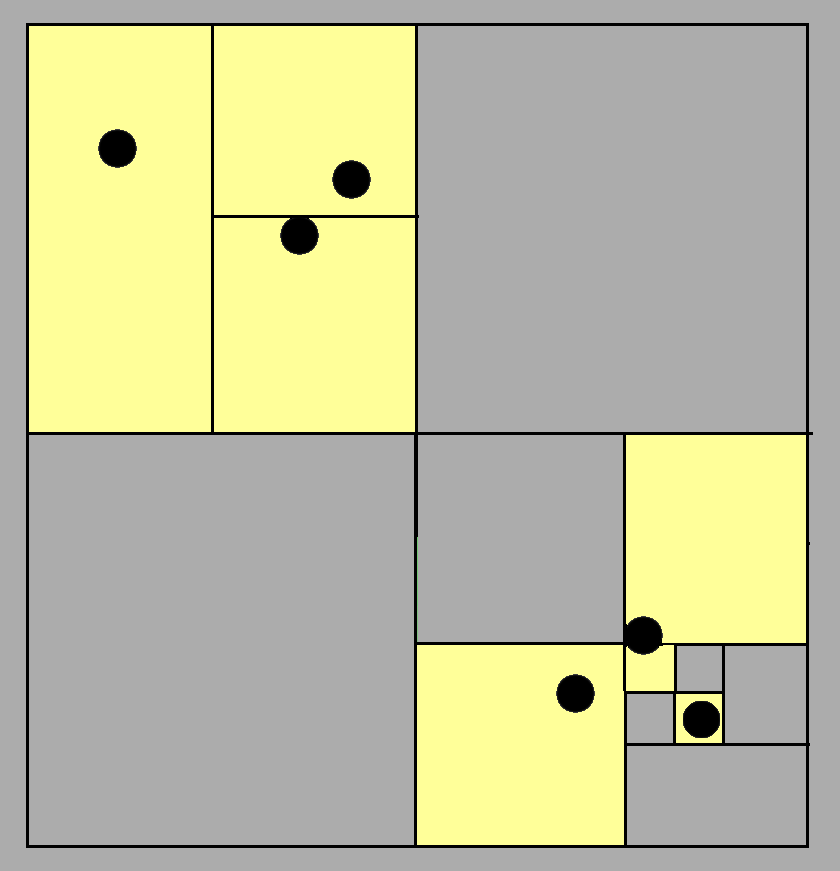
- 八叉树
它类似于四叉树,但有 8 个节点。如果你的 3D 游戏包含不同高度级别的元素,那么八叉树就很不错了。

- BSP(二进制空间分区)
这是一种非常快速的算法,允许你使用片段来分割空间。你将定义一个片段,然后算法将对对象是位于该片段的前面还是后面进行排序。它对于地图、城市、地牢非常有用......如果您生成地图并且可以快进,则可以同时创建片段。
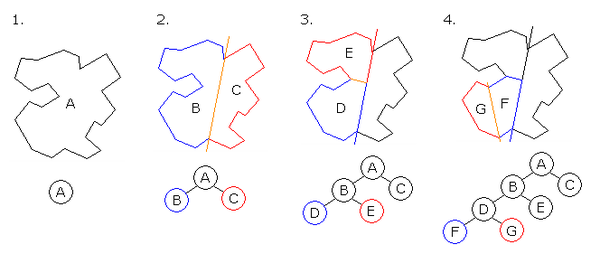
还有很多其他方法,请保持好奇心。我没有实现这些方法中的每一个,我只是为了知道它们存在,以防有一天我需要特定的空间分区。如果您使用多线程,某些算法非常适合并行化,例如八叉树或四叉树,并且还必须在您的决定上保持平衡。
- 计算着色器
计算着色器允许你在着色器上处理计算。只有当你有高度并行化的任务(例如使用简单的边界列表检查碰撞)时,才必须使用此技术。我从未为视锥体剔除实现过这种技术,但如果你有很多移动的对象,则可以在这种情况下使用它来避免更新空间分区。
原文链接:视锥体剔除 - BimAnt