高斯泼溅(Gaussian Splatting)是一种表示 3D 场景和渲染新视图的方法,在"实时辐射场渲染的 3D 高斯泼溅" 中引入。它可以被认为是 NeRF 类模型的替代品,就像当年的 NeRF 一样,高斯泼溅引发了大量新的研究工作,这些研究选择将其用作各种用例的 3D 世界的底层表示。那么它有什么特别之处,为什么它比 NeRF 更好呢?或者说,它真的比 NeRF 更好吗?让我们来一探究竟吧!
TL;DR
首先,从标题就可以看出,这项工作最出名的地方是高渲染速度。这要归功于下面将要介绍的表示本身,以及使用自定义 CUDA 内核定制实现的渲染算法。

图 1:在渲染速度(fps)、训练时间(分钟)和视觉质量(峰值信噪比,越高越好)方面,之前的高质量表示和高斯分布(标记为"我们的")的并排比较
此外,高斯分布根本不涉及任何神经网络。甚至没有一个小型的 MLP,没有任何"神经",场景本质上只是空间中的一组点。这本身就已经吸引了人们的注意力。在我们痴迷于人工智能的世界中,研究公司追逐由越来越多的数十亿个参数组成的模型,看到这种方法越来越受欢迎,这令人耳目一新。其理念源自"表面溅射"³ (2001),因此它树立了一个很酷的例子,表明经典的计算机视觉方法仍然可以启发相关的解决方案。其简单而明确的表示使高斯溅射特别易于解释,这是在某些应用中选择它而不是 NeRF 的一个很好的理由。
2、3D 世界的表示
如前所述,在高斯分布中,3D 世界由一组 3D 点表示,实际上有数百万个 3D 点,数量大约为 50 万到 500 万。每个点都是一个 3D 高斯,具有自己独特的参数,这些参数根据场景进行拟合,以便该场景的渲染与已知的数据集图像紧密匹配。优化和渲染过程将在后面讨论,因此我们暂时先讨论必要的参数。

图 2:高斯中心(均值)
每个 3D 高斯都由以下参数化:
- 均值 μ, 可解释为位置 x、y、z;
- 协方差 Σ;
- 不透明度 σ(𝛼),应用 S 型函数将参数映射到 [0, 1] 区间;
- 颜色参数,(R、G、B) 的 3 个值或球谐函数 (SH) 系数。
这里有两组参数需要进一步讨论,即协方差矩阵和 SH。有专门讨论后者的单独部分。至于协方差,它在设计上被选择为各向异性的,也就是说,不是各向同性的。实际上,这意味着 3D 点可以是沿空间中任何方向旋转和拉伸的椭圆体。它可能需要 9 个参数,但是它们无法直接优化,因为协方差矩阵只有在为半正定矩阵时才具有物理意义。使用梯度下降进行优化很难直接对矩阵施加此类约束,因此它被分解为如下形式:

这种分解称为协方差矩阵的特征分解,可以理解为椭圆体的配置,其中:
- S 是一个对角缩放矩阵,具有 3 个缩放参数;
- R 是一个 3x3 旋转矩阵,用 4 个四元数解析表示。
使用高斯函数的妙处在于每个点都有双重影响。一方面,根据其协方差,每个点实际上代表了接近其均值的空间有限区域。另一方面,它具有理论上无限的范围,这意味着每个高斯函数都定义在整个 3D 空间中,并且可以针对任何点进行评估。这很棒,因为在优化过程中,它允许梯度从远距离流动。⁴
3D 高斯函数 i 对 3D 中任意 3D 点 p 的影响定义如下:

图 3:3D 高斯 i 对 3D 中点 p 的影响
该方程看起来几乎像多元正态分布的概率密度函数,只是忽略了具有协方差决定因素的正则化项,而是通过不透明度进行加权。
3、图像形成模型
给定一组 3D 点,可能最有趣的部分是看看它如何用于渲染。你可能之前熟悉 NeRF 中使用的逐点 𝛼 混合。事实证明,NeRF 和高斯 splatting 共享相同的图像形成模型。为了了解这一点,让我们稍微绕道并重新查看 NeRF² 中给出的体积渲染公式及其许多后续作品 (1)。我们还将使用简单的过渡重写它 (2):
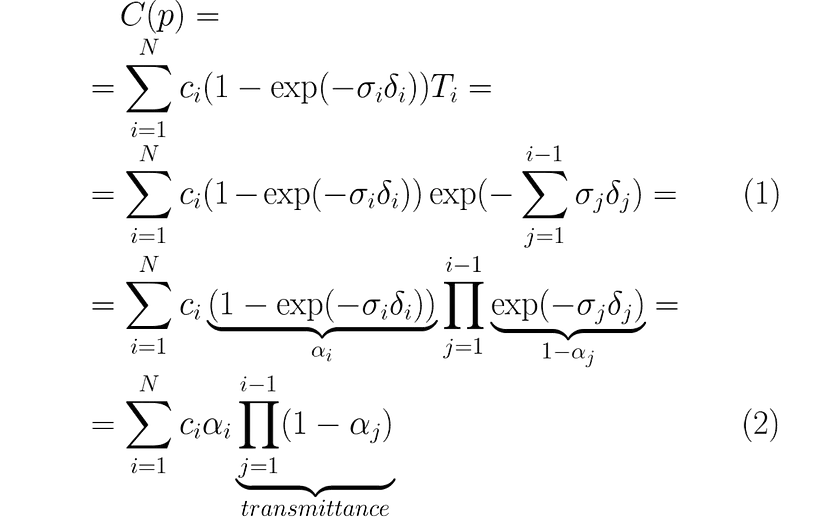
你可以参考 NeRF 论文了解 σ 和 δ 的定义,但从概念上讲,可以这样理解:在 NeRF 中,图像像素 p 中的颜色是通过沿着穿过该像素的射线对样本(MLP 预测)进行积分来近似的。最终颜色是沿着该射线采样的 3D 点颜色的加权和,通过透射率降低权重。考虑到这一点,让我们最后看一下高斯溅射的图像形成模型:

实际上,公式 (2) 和 (3) 几乎完全相同。唯一的区别在于两者之间如何计算 𝛼。在高斯溅射中,每个像素的聚合都是通过投影的 2D 高斯的有序列表的贡献进行的。这种微小的差异在实践中变得极为重要,并导致渲染速度截然不同。事实上,这是高斯溅射实时性能的基础。
要理解为什么会出现这种情况,我们需要了解 f^{2D} 的含义以及它提出了哪些计算要求。这个函数只是我们在上一节中看到的 f(p) 在 2D 中的投影,即在正在渲染的相机的图像平面上的投影。 3D 点及其投影都是多元高斯函数,因此可以使用与 3D 高斯函数对 3D 中其他点的影响相同的公式来计算投影的 2D 高斯函数对像素的影响(见图 3)。唯一的区别是,均值 μ 和协方差 Σ 必须投影到 2D 中,这可以使用 EWA splatting⁵ 的推导来完成。
通过使用固有相机矩阵 K 和外部相机矩阵 W=[R|t],将齐次坐标中的向量 μ(带有额外的 1 个坐标)投影到图像平面,可以轻松获得 2D 中的均值:

也可以用一行来写,如下所示:

这里"z"下标代表 z 标准化。二维中的协方差使用雅可比矩阵 (4) J 定义:

整个过程仍然是可微分的,这对于优化当然至关重要。
3、渲染
公式 (3) 告诉我们如何在单个像素中获得颜色。要渲染整个图像,仍然需要遍历所有 HxW 像素,就像在 NeRF 中一样,但是,该过程要轻量得多,因为:
对于给定的相机,每个 3D 点的 f(p) 可以预先投影到 2D 中,然后再迭代像素。这样,当高斯分布与几个附近的像素混合时,我们就不需要一遍又一遍地重新投影它了。
没有 MLP 需要对单个图像进行 H·W·P 次推理,2D 高斯分布直接混合到图像上。
在射线上评估哪个 3D 点没有歧义,无需选择射线采样策略。与每个像素的射线重叠的一组 3D 点(参见 (3) 中的 N)在优化后是离散的和固定的。
在 GPU 上,使用可微分 CUDA 内核的自定义实现,每帧进行一次预处理排序阶段。
概念上的差异可以在图 4 中看到:

图 4:NeRF 和 GS 之间的概念差异,左:沿射线查询连续 MLP,右:混合与给定射线相关的一组离散高斯
上面提到的排序算法是本文的贡献之一。其目的是使用公式 (3) 为颜色渲染做准备:按深度(与图像平面的接近度)对 3D 点进行排序,并按图块对它们进行分组。前者是计算透射率所必需的,后者允许将每个像素的加权和限制为仅对相关 3D 点(或更具体地说,它们的 2D 投影)进行 α 混合。分组是使用简单的 16x16 像素图块实现的,并且实现方式是,如果高斯与多个视锥体重叠,则可以落在几个图块中。由于排序,每个像素的渲染可以简化为像素所属图块中预先排序的点的 α 混合。

图 5:视锥体,每个视锥体对应一个 16x16 图像块。颜色没有特殊含义。排序算法的结果是每个块内按深度排序的 3D 点子集。
4、优化
一个幼稚的问题可能会浮现在脑海中:如何从空间中的一堆斑点中获得一张看起来不错的图像?好吧,如果高斯函数没有得到适当的优化,渲染中就会出现各种尖锐的伪影。在图 6 中,您可以观察到此类伪影的一个例子,它们看起来非常像椭圆体。获得良好渲染的关键是 3 个组件:良好的初始化、可微分优化和自适应致密化。

图 6:未优化场景的渲染示例
初始化是指在训练开始时设置的 3D 点的参数。对于点位置(均值),作者建议使用由 SfM(运动结构)生成的点云,见图 7。逻辑是,对于任何 3D 重建,无论是使用 GS、NeRF 还是更经典的方法,你都必须知道相机矩阵,因此你可能还是会运行 SfM 来获取这些矩阵。由于 SfM 会产生稀疏点云作为副产品,为什么不使用它进行初始化呢?这就是本文所建议的。当由于某种原因无法获得点云时,可以使用随机初始化,但可能会损失最终重建质量。

图 7:SfM 生成的稀疏 3D 点云,均值初始化
协方差被初始化为各向同性,换句话说,3D 点以球体开始。半径是根据到相邻点的平均距离设置的,这样 3D 世界就可以很好地覆盖,没有"洞"。
初始化后,使用简单的随机梯度下降来正确拟合所有内容。场景针对损失函数进行了优化,该函数是地面真实视图和当前渲染之间的 L1 和 D-SSIM(结构差异指数测量)的组合。
然而,这还不是全部,另一个关键部分仍然存在,那就是自适应致密化。它在训练期间偶尔启动一次,比如每 100 个 SGD 步骤,其目的是解决重建不足和过度重建的问题。需要强调的是,SGD 本身只能调整现有点。但在完全缺乏点或点太多的区域,很难找到好的参数。这就是自适应致密化的作用所在,它分割梯度大的点(图 8),并删除已经收敛到非常低的 α 值的点(如果一个点如此透明,为什么要保留它?)。

图 8:自适应致密化。一个玩具示例,用几个点来拟合我们想要渲染的豆形
5、使用 SH 的视图相关颜色
球谐函数,简称 SH,在计算机图形学中起着重要作用,最初被提出作为一种学习 Plenoxels⁶ 中离散 3D 体素的视图相关颜色的方法。视图依赖性是一种很好的属性,它可以提高渲染质量,因为它允许模型表示非朗伯效应,例如金属表面的镜面反射。然而,这当然不是必须的,因为可以进行简化,选择用 3 个 RGB 值表示颜色,并且仍然使用高斯溅射,就像在 [4] 中所做的那样。这就是为什么我们在布置整个方法之后单独审查这个表示细节。
SH 是在球体表面上定义的特殊函数。换句话说,你可以对球体上的任何一点求出这样的函数并得到一个值。所有这些函数都是从这个单一公式中推导出来的,通过为 ℓ 和 −ℓ ≤ m ≤ ℓ 选择正整数,每个 SH 一个 (ℓ, m) 对:
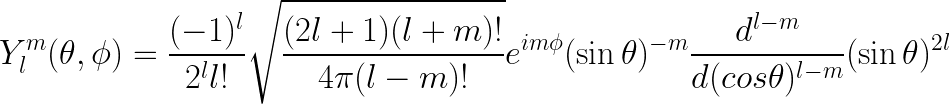
虽然一开始有点吓人,但对于较小的 l 值,这个公式会大大简化。事实上,对于 ℓ = 1,Y = ~0.282,只是整个球面上的一个常数。相反,较高的 ℓ 值会产生更复杂的表面。理论告诉我们,球谐函数形成一个正交基,因此球面上定义的每个函数都可以通过 SH 来表达。
这就是为什么表达视点相关颜色的想法是这样的:让我们将自己限制在一定的自由度 ℓ_max 上,并说每种颜色(红色、绿色和蓝色)都是前 ℓ_max 个 SH 函数的线性组合。对于每个 3D 高斯,我们都希望学习正确的系数,以便当我们从某个方向看这个 3D 点时,它将传达最接近地面真实颜色的颜色。获取视点相关颜色的整个过程可以在图 9 中看到。
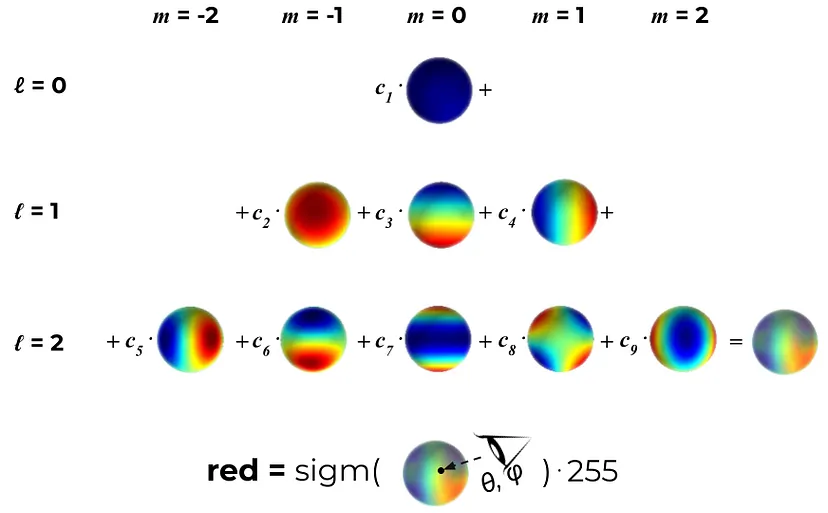
图 9:获取 ℓ_max = 2 且有 9 个学习系数的点的视图相关颜色(红色分量)的过程。S 型函数将值映射到 [0, 1] 区间。通常,会改用裁剪
6、限制
尽管总体效果很好且渲染速度惊人,但表示的简单性是有代价的。最重要的考虑是在优化过程中引入的各种正则化启发式方法,以防止模型出现"破碎的"高斯分布:点太大、太长、冗余等。这部分至关重要,提到的问题可以在新视图渲染之外的任务中进一步放大。
选择放弃连续表示而采用离散表示意味着 MLP 的归纳偏差会丢失。在 NeRF 中,MLP 执行隐式插值并消除给定视图之间可能存在的不一致,而 3D 高斯则更为敏感,这又回到了上面描述的问题。
此外,高斯溅射并不能摆脱 NeRF 中存在的一些众所周知的伪影,它们都从共享图像形成模型中继承了这些伪影:在较少看到或未看到区域的质量较低、靠近图像平面的漂浮物等。
检查点的文件大小是另一个需要考虑的属性,即使新颖的视图渲染还远未部署到边缘设备。考虑到 3D 点的大致数量和流行 NeRF 的 MLP 架构,两者都占用相同数量级的磁盘空间,而 GS 的平均重量仅是后者的几倍。
7、在哪里试用
没有一篇博客文章可以像运行并亲眼看到结果一样公正地介绍一种方法。你可以在这里试用:
- gaussian-splatting --- 使用自定义 CUDA 内核的官方实现;
- nerfstudio--- 是的,nerfstudio 中的高斯 splatting。这是一个最初专用于 NeRF 类模型的框架,但自 23 年 12 月以来,它也支持 GS;
- threestudio-3dgs --- 另一个跨模型框架 threestudio 的扩展。如果你有兴趣从提示生成 3D 模型而不是学习现有的一组图像,则应该使用这个;
- UnityGaussianSplatting --- 如果你喜欢 Unity,可以将训练好的模型移植到这个插件中进行可视化;
- gsplat --- 一个从 nerfstudio 分支出来的用于 CUDA 加速高斯光栅化的库。它可以作为 splatting 的可区分模块用于独立的基于 torch 的项目。
原文链接:高斯泼溅综合指南 - BimAnt