直流电机重要参数
直流电机作为一个电磁装置,对于用户来说要哪些参数是他们关注的呢。
• 额定功率PN:电机在铭牌规定的额定状态下运行时电机的输出功率(W/kW)
• 额定电压UN:电机出线端额定电压(V )
• 额定电流IN:电机出线额定电流(A)
• 额定转速nN:(r/min,r.p.m)
• 额定励磁电压UfN:(V)
• 额定励磁电流IfN: (A)
• 额定效率ŋN: (%)
发电机: P N = U N ⋅ I N P_N = U_N \cdot I_N PN=UN⋅IN
电动机: P N = U N ⋅ I N ⋅ η N P_N = U_N \cdot I_N \cdot \eta_N PN=UN⋅IN⋅ηN
直流电机磁场分析
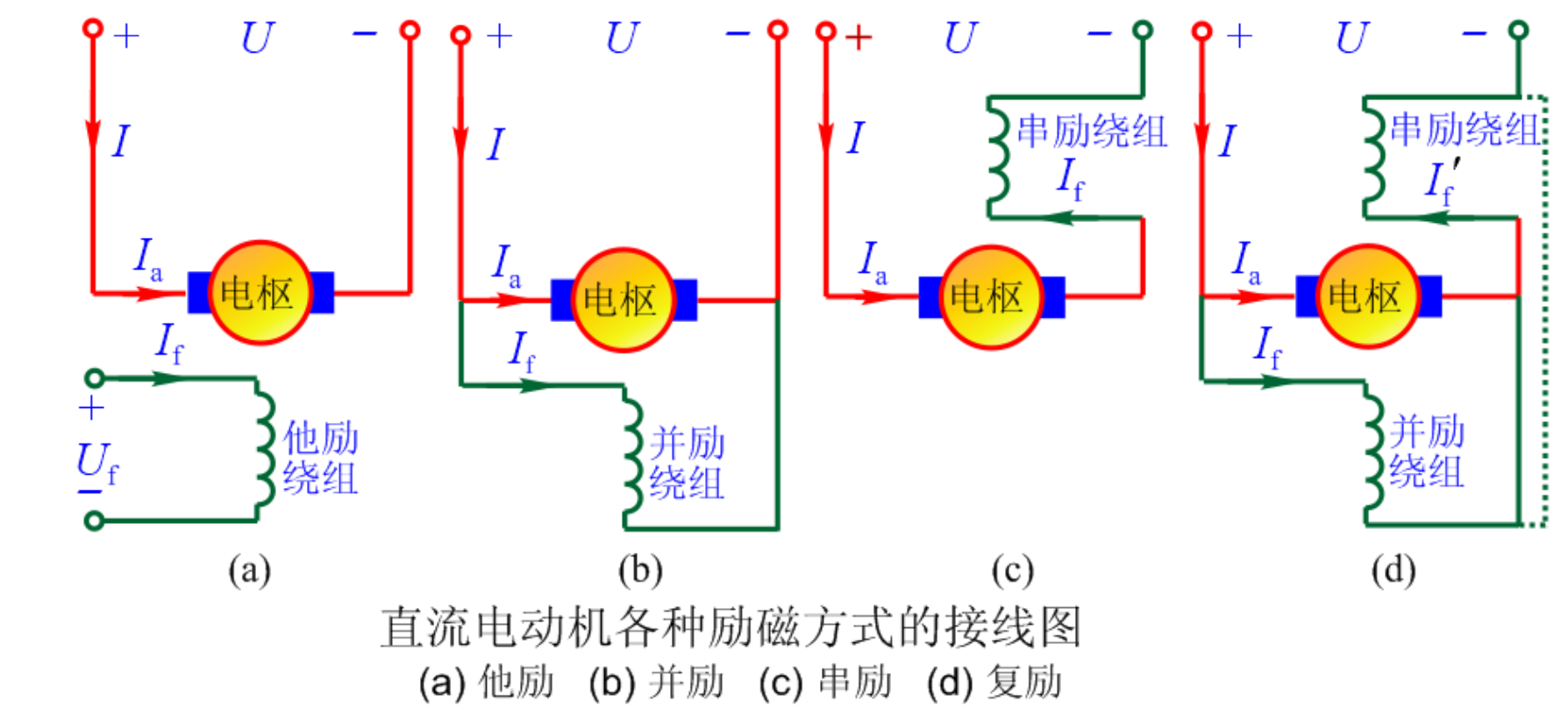
直流电机的四种励磁方式:
直流电机空载磁场分析
空载的特点:
• 输出功率为零
• 有损耗存在,电动机电枢电流≠0
理想空载
• 电枢电流为零且 转速≠0
• 电机中的磁场完全由主极绕组产生
空载磁场
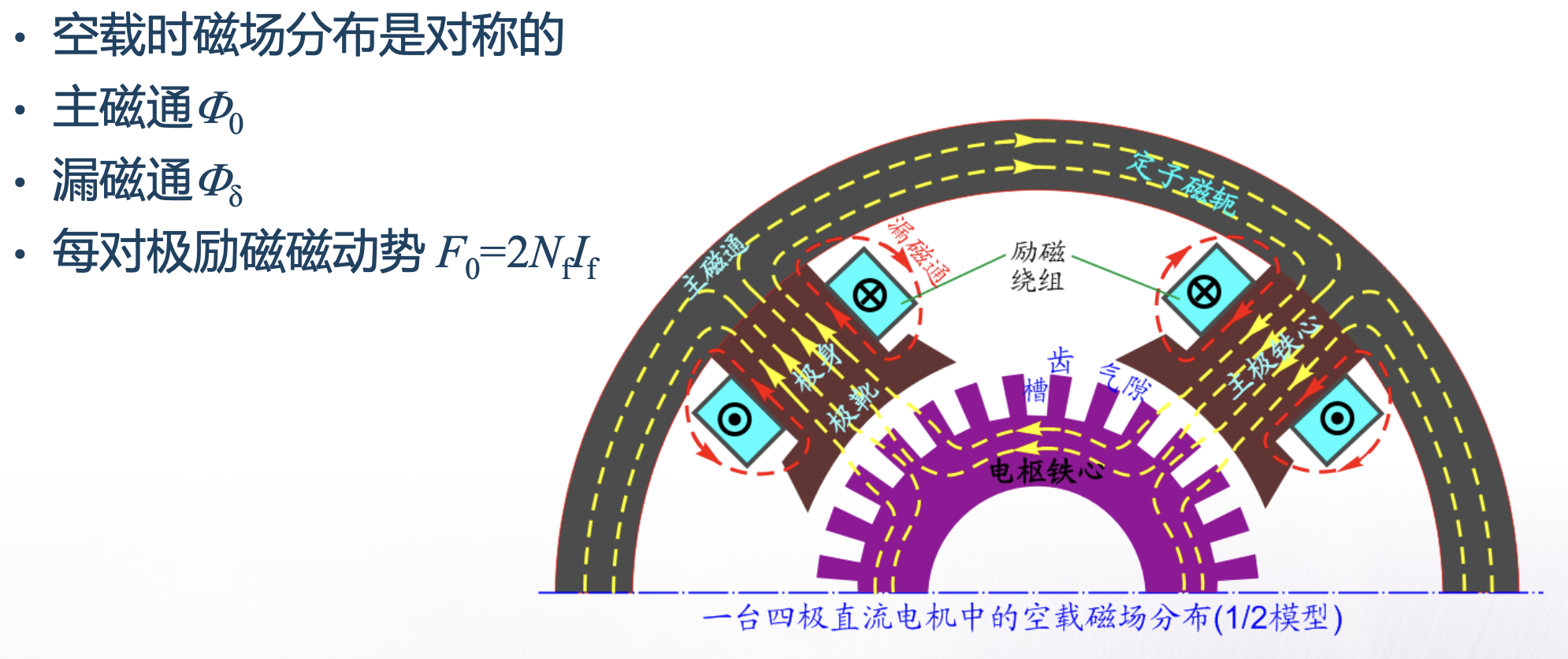
• 主磁通在转子导体(电枢绕组)中产生感应电势
• 漏磁通不产生感应电势,可能引起主极铁心饱和,增大磁路磁阻
空载气隙磁场分布
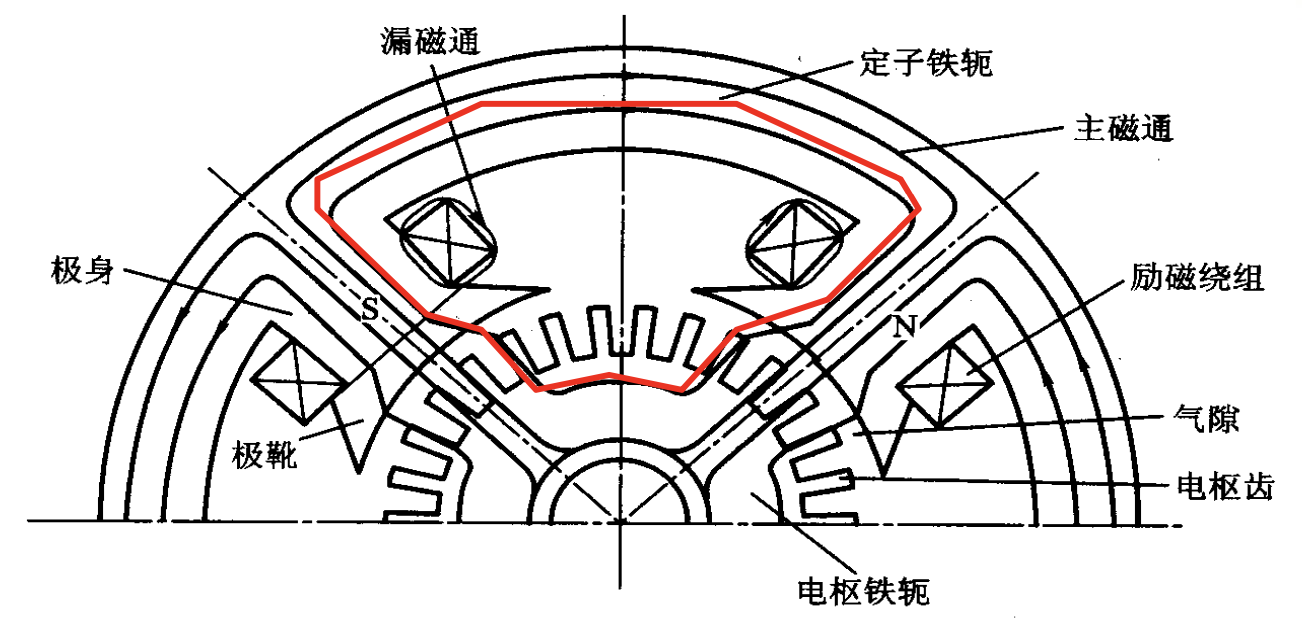
假设
• 铁磁材料μ→∞
• 不计齿槽影响
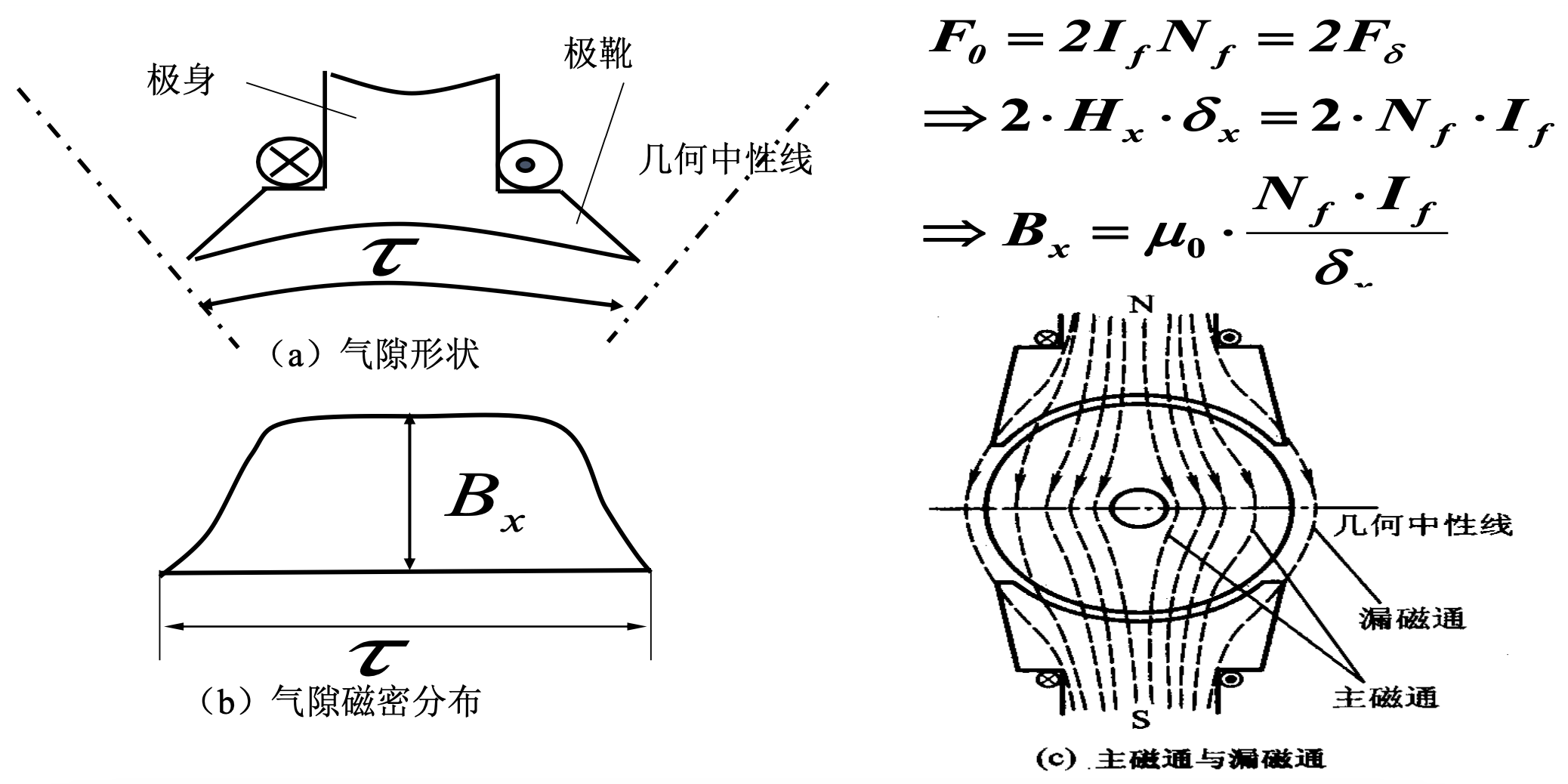
F 0 = ∮ H ⋅ d l = 2 I f N f = 2 F δ + F 定子轭 + 2 F 定子齿 + F 转子轭 + 2 F 转子齿 ≈ 2 F δ F_0 = \oint H \cdot dl = 2I_f N_f = 2F_{\delta} + F_{\text{定子轭}} + 2F_{\text{定子齿}} + F_{\text{转子轭}} + 2F_{\text{转子齿}} \approx 2F_{\delta} F0=∮H⋅dl=2IfNf=2Fδ+F定子轭+2F定子齿+F转子轭+2F转子齿≈2Fδ
空载时,主磁通与空载磁动势或空载励磁电流的关系。
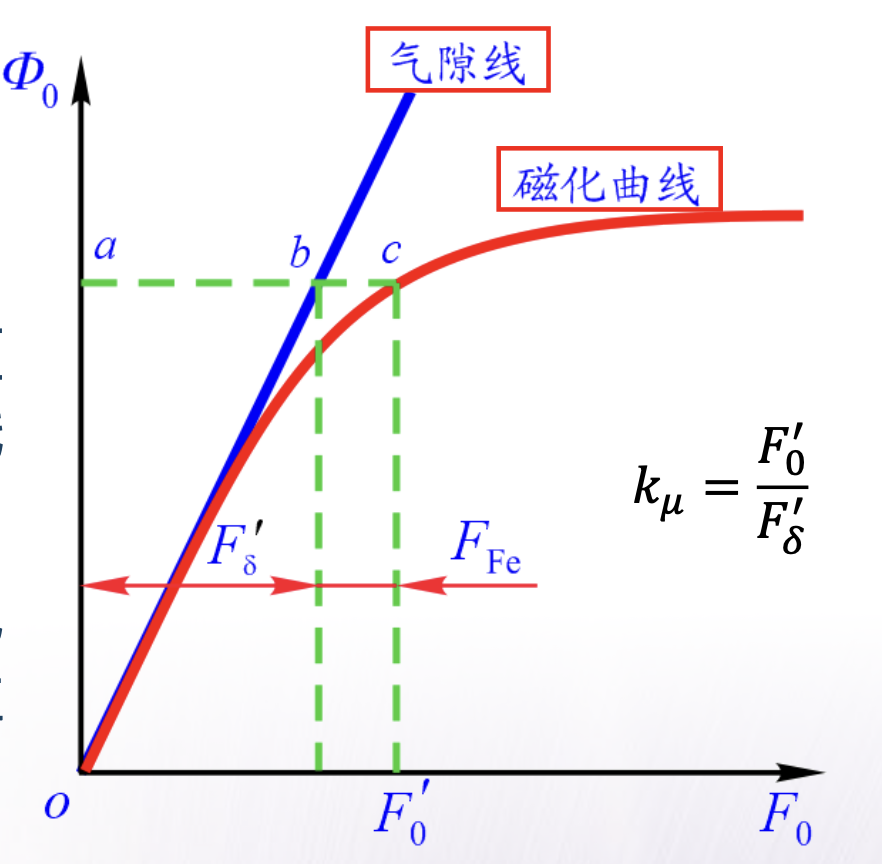
直流电机的磁化曲线: Φ 0 = f ( F 0 ) 或 Φ 0 = f ( I f ) \Phi_0 = f(F_0) \quad \text{或} \quad \Phi_0 = f(I_f) Φ0=f(F0)或Φ0=f(If)
- 饱和系数 k k k: 空载运行时,产生额定电枢电压所需磁动势 F 0 F_0 F0,与同一磁通下气隙线上的磁动势 F ′ F' F′ 的比值
- 为了经济、合理地利用材料,一般直流电机额定运行时,额定磁通设定在磁化特性曲线开始进入饱和区的位置
负载磁场-电枢反应
• 电机负载时,电枢电流不为零,存在电枢磁势。
空载: F δ = F f F_{\delta} = F_{f} Fδ=Ff
负载: F δ = F f + F a F_{\delta} = F_{f} + F_{a} Fδ=Ff+Fa
• 气隙磁场由主极磁势和电枢磁势共同建立。
• 电枢磁场对气隙磁场的影响称为电枢反应。
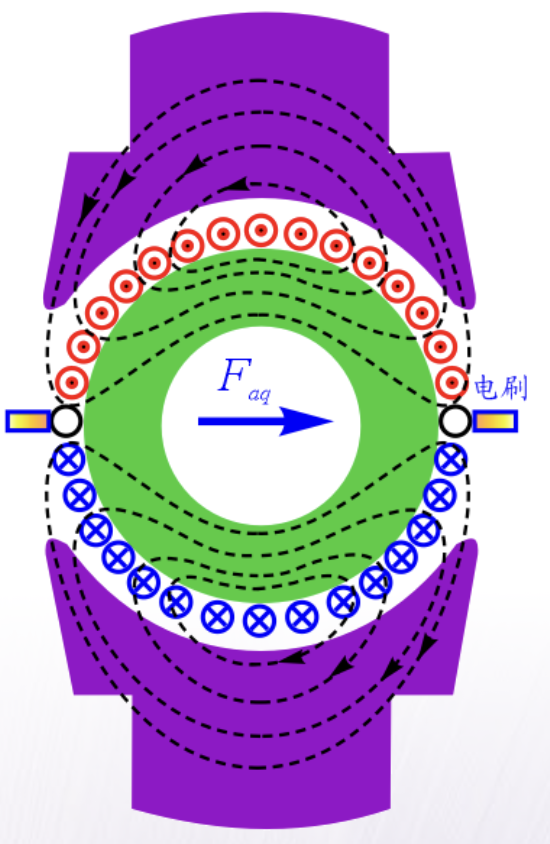
•当电刷在几何中性线上时电枢磁势-交轴电枢磁势
• 线负荷-在电枢表面单位长度上的安培导体数,用A表示。 A = N i a π D a A = \frac{N i_a}{\pi D_a} A=πDaNia
• 主磁极的中心线称为直轴(d轴)
• 相邻N极和S极的分界线称为交轴(q轴)
• 一般情况下,直流电机电枢磁场方向总是对准交轴,称为交轴电枢磁场
电枢磁动势和磁场分布关系
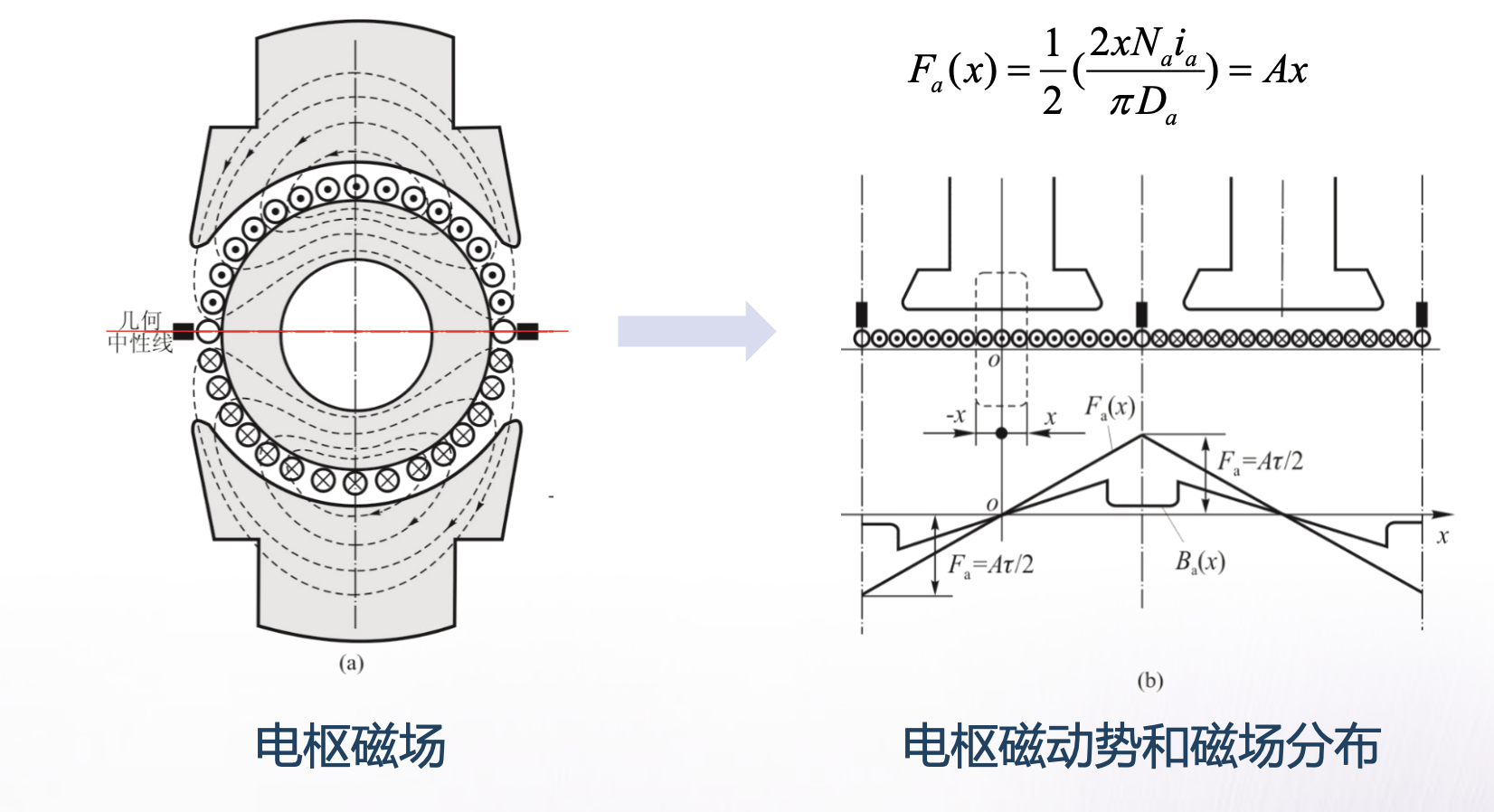
单独考虑电枢磁场。图中根据右手螺旋定则示意性地给出了电枢电流所建立的磁场的分布情况。将电枢沿几何中性线处展开成直线,画出电刷和主极,以主极轴线与电枢表面的交点为原点0,如右图所示。在一极距范围内,取距原点为+x和-x的两点形成一矩形回路,该回路包围的总电流数为 2 x N a i a π D a , N a 为电枢导体数, i a 为导体电流, D a 为电枢外径 \frac{2xN_a i_a }{ π D_a},N_a为电枢导体数,i_a为导体电流,D_a为电枢外径 πDa2xNaia,Na为电枢导体数,ia为导体电流,Da为电枢外径。而由全电流定律可知,这也就是消耗在该回路各段磁路上的总的磁动势。设铁磁材料中的磁压降忽略不计,即全部磁动势都消耗在两个气隙上,则x处的电枢磁动势为
F a ( x ) = 1 2 ( 2 x N a i a π D a ) = ( N a i a π D a ) x = A x F_a(x) = \frac{1}{2} (\frac{2xN_a i_a }{ π D_a}) = (\frac{N_a i_a }{π D_a}) x = Ax Fa(x)=21(πDa2xNaia)=(πDaNaia)x=Ax
式中, A = N a i a π D a A = \frac{N_a i_a }{ π D_a } A=πDaNaia为电机的绕组负荷,表示沿电枢表面单位长度上安培导体数。
在-π/2≤x≤π/2之间,可方便地画出电枢磁动势沿电枢表面的分布,如右图下部所示。图中规定磁场方向以从电枢指向主极为正,反之为负。结果表明,电枢磁动势沿空间的分布为三角形奇函数,在主极轴线处过零,在几何中性线处有最大值
F a = A π 2 F_a = \frac{Aπ} { 2} Fa=2Aπ
可见,当电刷放在几何中性线上时,电枢磁动势的轴线也在几何中性线上,恰与主极 轴线正交(无论主极对数多少,总是在空间上相差 90°电角度,仅在 p =1 时,电角度才与机 械角度相等),故通常称之为交轴电枢磁动势,其最大值记为 _F_aq,即
图片中的文字内容如下:
F a q = F a = A π 2 F_aq = F_a = \frac{Aπ} { 2} Faq=Fa=2Aπ
以上分析是基于电枢表面无槽而且导体均匀分布进行的。若电枢有槽,导体放在槽中,则虽然 F a ( x ) F_a(x) Fa(x)的奇函数特征不变,但分布形状却会由三角形变为阶梯形。
已知电枢磁动势沿气隙的分布,即可求得电枢磁场产生的磁通密度沿气隙的分布为
B a ( x ) = μ 0 H a ( x ) = μ 0 F a ( x ) δ ( x ) = μ 0 A x δ ( x ) B_a(x) = μ_0 H_a(x) = μ_0 \frac{F_a(x)} { δ(x)} = μ_0 \frac{Ax} { δ(x)} Ba(x)=μ0Ha(x)=μ0δ(x)Fa(x)=μ0δ(x)Ax
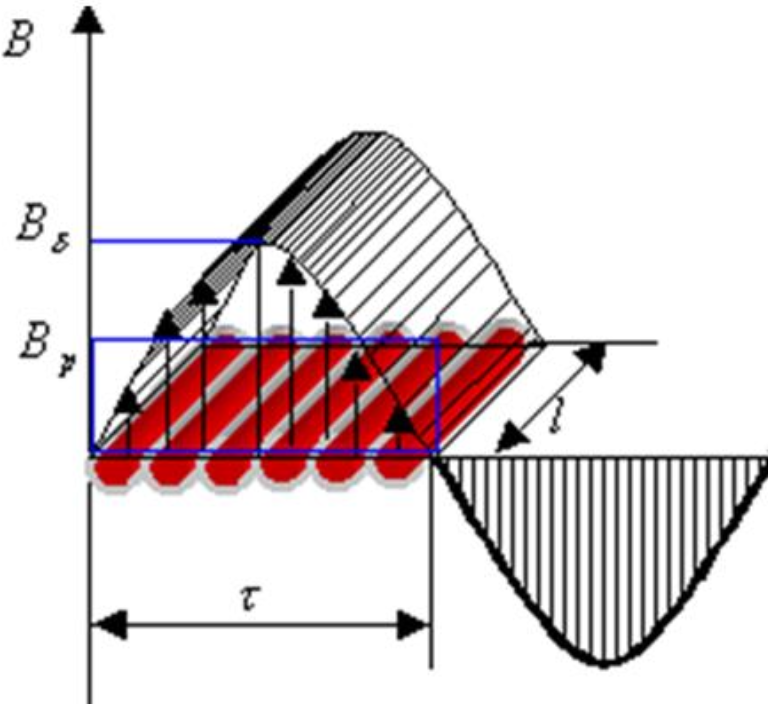
由于主极下的气隙不均匀,并且相邻两主极间的气隙很大,因此磁通密度的分布曲线如右图所示的马鞍形。
交轴电枢反应:交轴电枢磁场对主极磁场的影响
对于任意一台负 载运行的电机来说,这两种磁场都是同时存在的;或者说,电机的负载磁场就是由二者共 同建立的,并且负载磁场与空载磁场之间的差别完全是电枢磁场作用的结果。
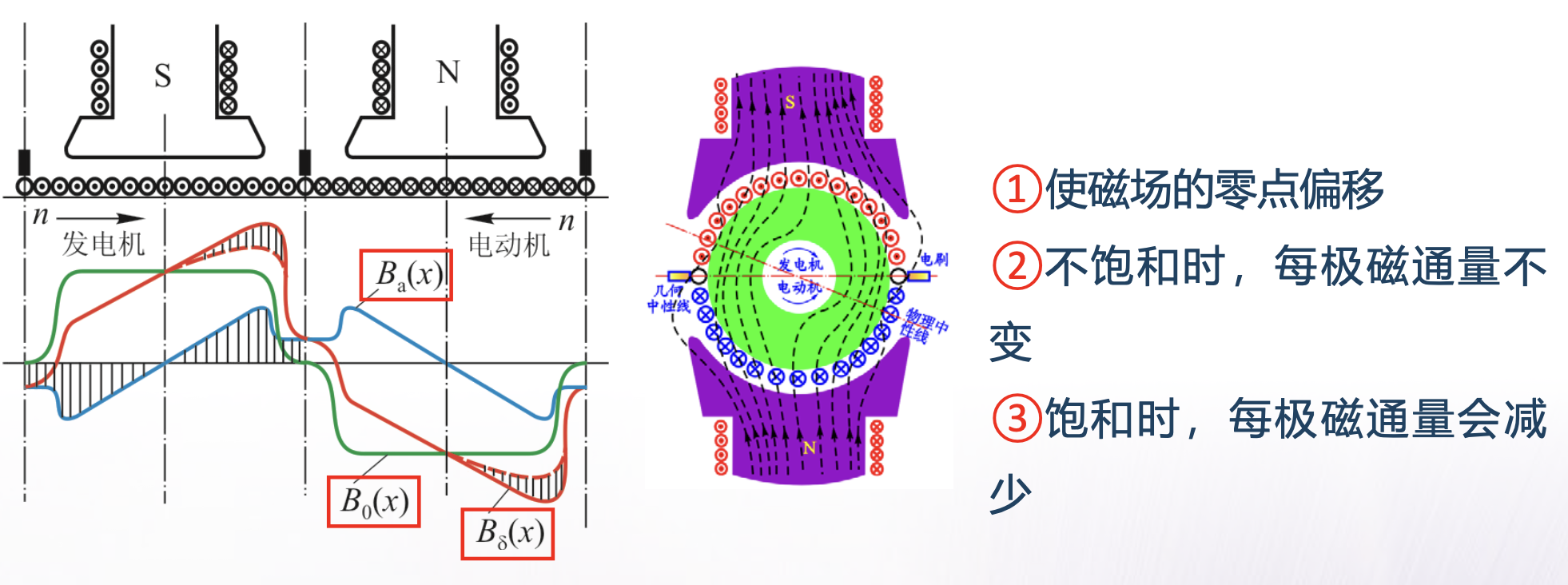
- 交轴电枢反应
电刷在几何中性线上时,电枢磁场只有交轴分量;电机磁场由励磁磁动势和交轴磁动势共同建立,如上图所示。 图中 B 0 ( x ) 为空载气隙磁密分布, B a ( x ) 为电枢磁场产生的气隙磁密分布, B y ( x ) 图中B_0(x)为空载气隙磁密分布,B_a(x)为电枢磁场产生的气隙磁密分布,B_y(x) 图中B0(x)为空载气隙磁密分布,Ba(x)为电枢磁场产生的气隙磁密分布,By(x)为合成气隙磁密波形。
从上图可见,合成后的气隙磁场不但波形发生了畸变,而且电枢上实际的几何中性线(即磁通密度的过零点)也偏移了一个α角度,我们把电枢表面磁通密度的实际过零点的连线称为物理中性线。
结合上图,交轴电枢反应对气隙磁场的影响概述如下:
(1)使物理中性线偏离几何中性线一个α角。对发电机,偏移为顺电枢转向;对电动机则是逆电枢转向。
(2)不计饱和影响,将 B a ( x ) 和 B 0 ( x ) 相加得合成磁场 B σ ( x B_a(x)和B_0(x)相加得合成磁场B_{\sigma}(x Ba(x)和B0(x)相加得合成磁场Bσ(x),如图中的实线所示。此时每个主极下的磁场,一半被削弱,但另一半被加强,总的磁通不变。
(3)计及饱和影响,合成磁场 B σ ( x ) B_{\sigma}(x) Bσ(x)为图中的虚线。对被削弱的一半来说,波形与不计饱和时相同;但对于被加强的一半,由于实际磁路中铁磁材料的饱和影响,磁密曲线会下降,因此,每极磁通量也会减少。
综上所述,实际电机中,交轴电枢反应不但使气隙磁场畸变,而且还有去磁作用。
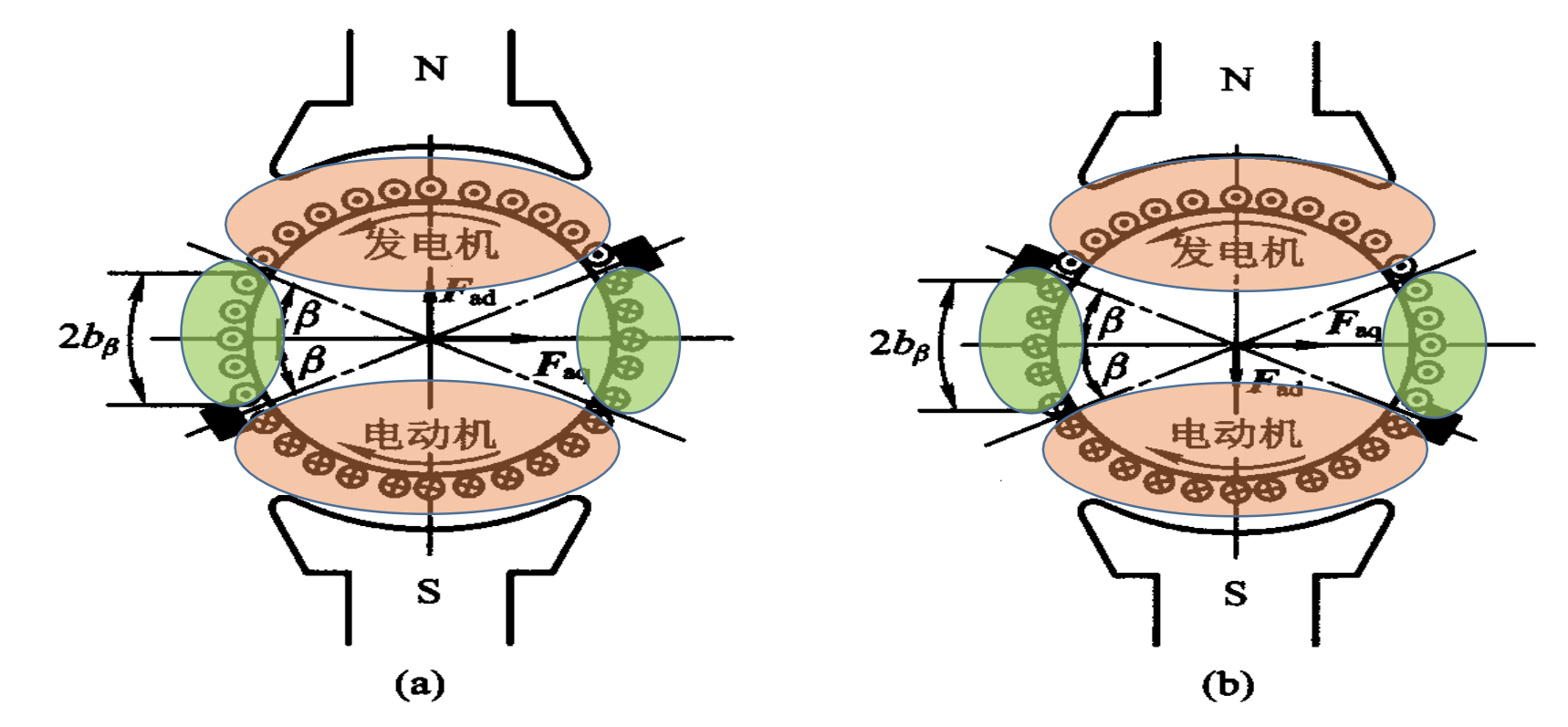
2.直轴电枢反应
电刷偏离几何中性线时,同时产生交轴电枢反应和直轴电枢反应。交轴电枢反应的性质同上,不重复讨论,这里只需要补充介绍直轴电枢反应的有关情况。
由于直轴电枢磁场轴线与主极轴线重合,因此其作用应该只是影响每极磁通的大小。参照上左图,以发电机为例,当电刷顺电枢转向从几何中性线偏移β角度时,直轴电枢磁场与励磁磁场方向相反,起去磁作用,使每极磁通量减少。反之,逆电枢转向偏移,如上图所示,直轴电枢磁场将起助磁作用。考虑饱和影响,此时每极磁通量Φ可把 F a q 与 F 0 F_{aq}与F_0 Faq与F0相加后通过电机的磁化曲线确定。
可以证明,电机作电动机运行时的情况正好与发电机相反,陈述从略。
感应电动势和电磁转矩
感应电动势和产生电磁转矩都是电枢绕组在气隙合成磁场中的电磁行为,前者是导体与磁场相对运动的结果,后者为磁场对载流导体的作用。
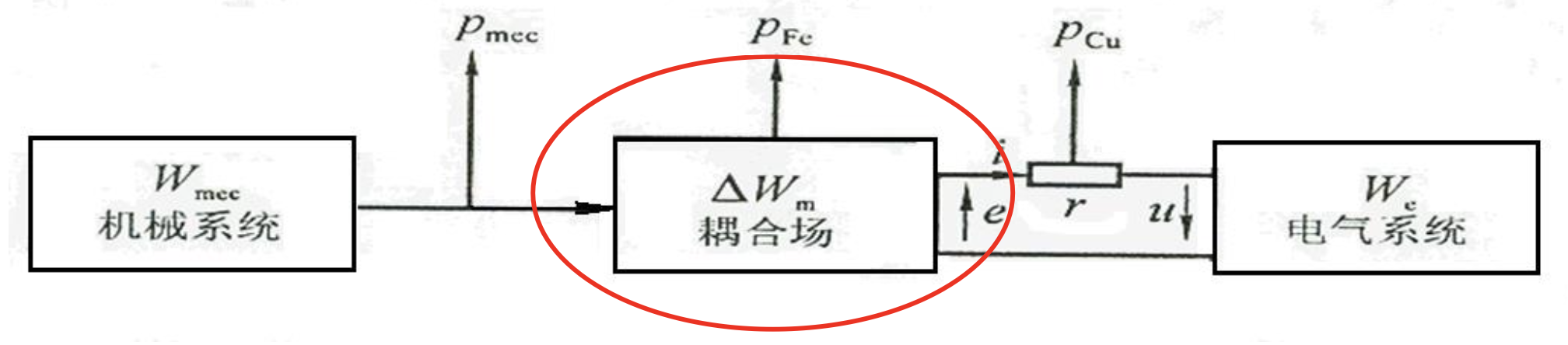
机电能量转换过程重要参数:这三个符号分别代表:
- E a : E_a: Ea:通常表示电枢电动势(Armature EMF),是电枢绕组产生的电动势。
- T e m T_em Tem:通常表示电磁转矩(Electromagnetic Torque),是电机中由电磁力产生的转矩。
- P e m : P_em: Pem:通常表示电磁功率(Electromagnetic Power),是电机中电磁转矩所做的功的功率。
感应电动势
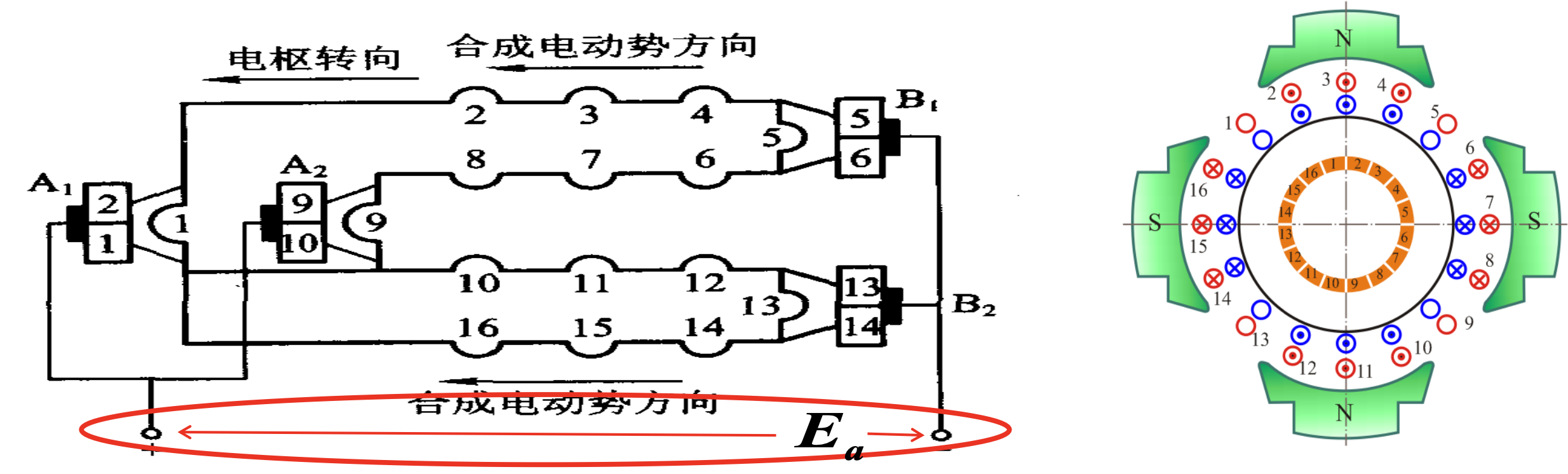
绕组元件的感应电动势由电磁感应定律计算。为简化推导,设绕组为整距,电刷在几何中性线上, N a N_a Na为电枢导体总数,每条支路的串联导体数为 N a / 2 a N_a / 2a Na/2a。由于第k根串联导体的感应电动势为
支路感应电动势 E a = ∑ x = 1 N a ( B x ⋅ l ⋅ v ) = l ⋅ v ⋅ ∑ x = 1 N a B x T e m = ∑ x = 1 N a T x 支路感应电动势 E_a = ∑{x=1}^{N_a}(B_x · l · v) = l · v · ∑{x=1}^{N_a}B_x \\ T_{em} = ∑_{x=1}^{N_a}T_x 支路感应电动势Ea=∑x=1Na(Bx⋅l⋅v)=l⋅v⋅∑x=1NaBxTem=∑x=1NaTx
其中, E a 表示支路感应电动势, B x 表示位置 x 处的磁通密度, l 表示导体长度, v 表示速度, T e m E_a 表示支路感应电动势,B_x 表示位置 x 处的磁通密度,l 表示导体长度,v 表示速度,T_{em} Ea表示支路感应电动势,Bx表示位置x处的磁通密度,l表示导体长度,v表示速度,Tem 表示电磁转矩, T x 表示位置 x 处的转矩 表示电磁转矩,T_x 表示位置 x 处的转矩 表示电磁转矩,Tx表示位置x处的转矩。
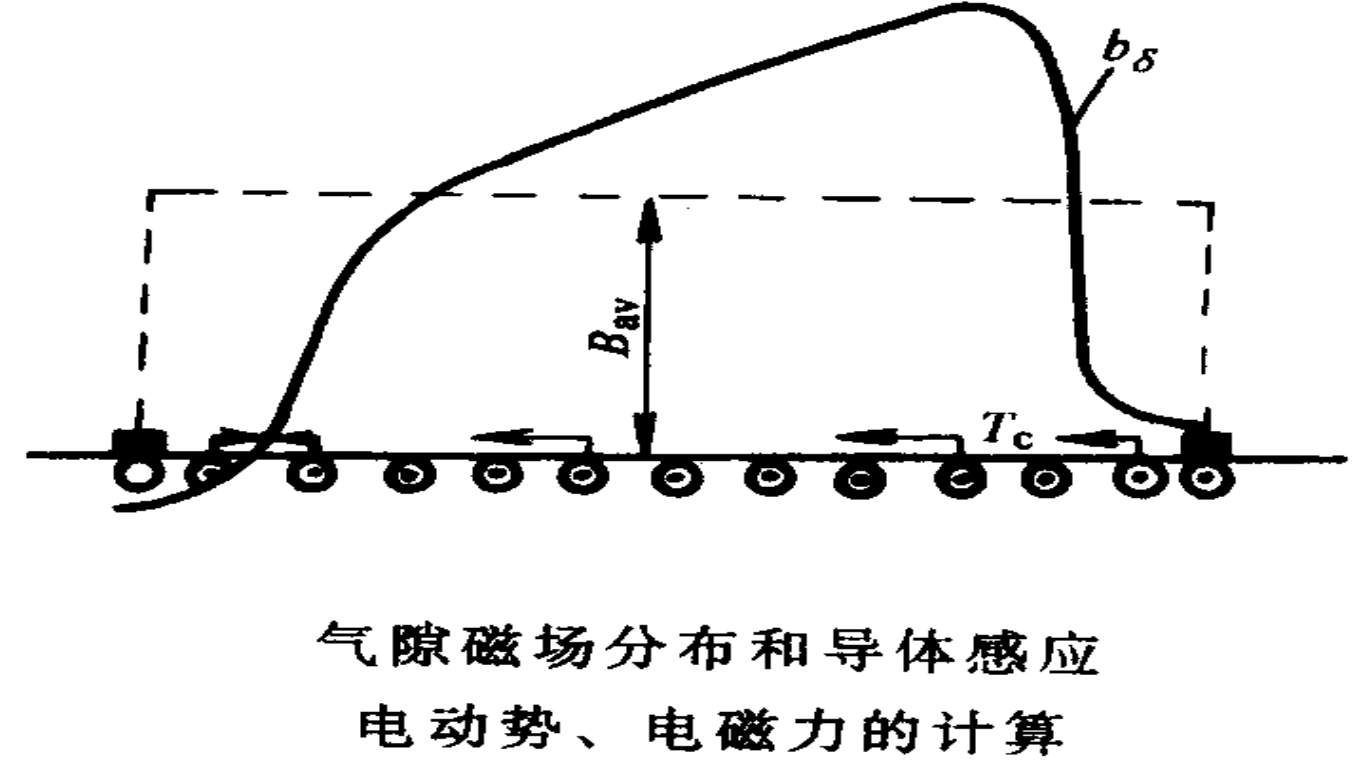
导体感应电势
e x = B x ⋅ l ⋅ v e_x = B_x \cdot l \cdot v ex=Bx⋅l⋅v
导体切割磁场速度
v = n 60 ⋅ 2 p ⋅ τ v = \frac{n}{60} \cdot 2p \cdot \tau v=60n⋅2p⋅τ
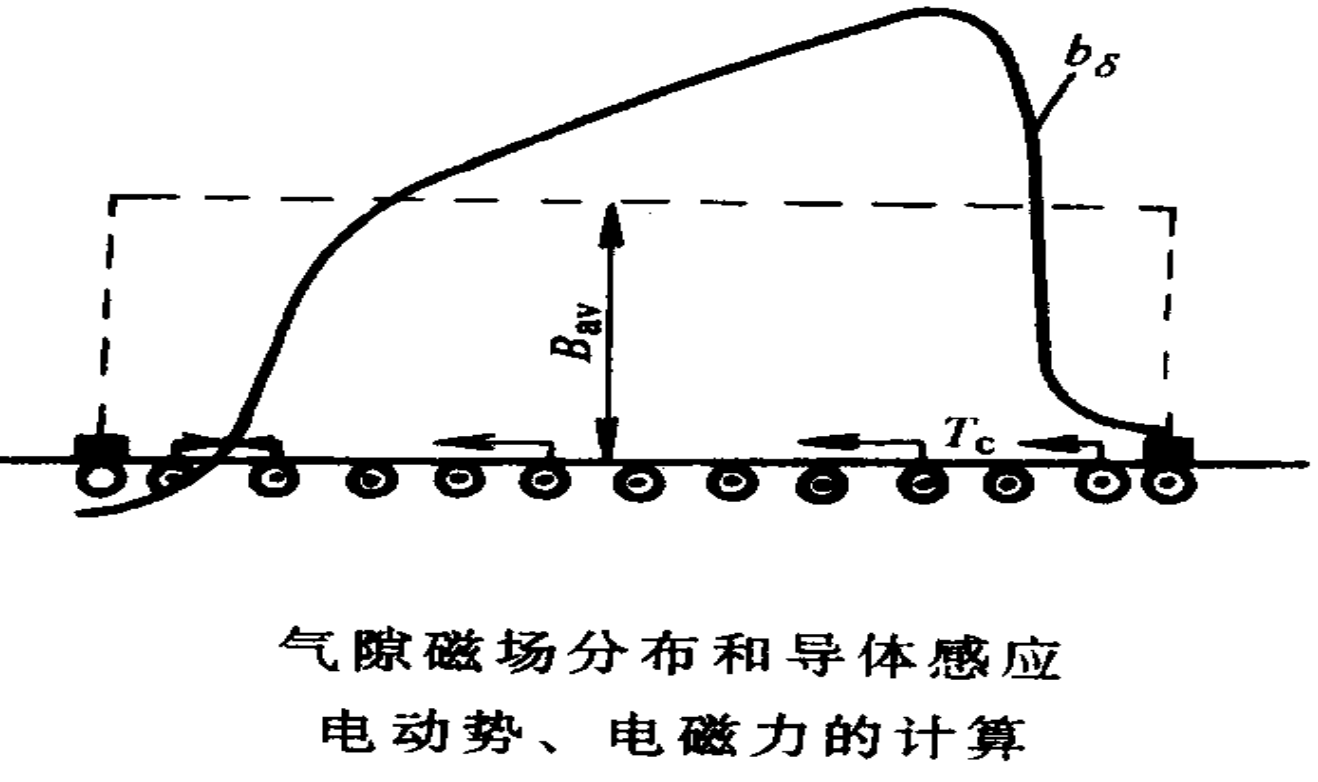
用平均磁通密度 B a B_a Ba。若将它综合成磁场的磁密分布 B a ( x ) B_a(x) Ba(x)。
设电枢绕组总导体数为N,有2a条并联支路
每条支路串联导体数 N a = N / 2 a N_a = N / 2a Na=N/2a
B a v = ∑ x = 1 N a B x N a = ∫ 0 τ B x ⋅ d x τ = ∫ 0 τ B x ⋅ l ⋅ d x τ ⋅ l = Φ τ ⋅ l B_{av} = \frac{∑_{x=1} ^{ N_a} B_x}{N_a} = \frac{∫_0 ^τ B_x · dx} { τ} = \frac{∫_0 ^ τ B_x · l · dx} {τ · l} = \frac{Φ}{ τ · l} Bav=Na∑x=1NaBx=τ∫0τBx⋅dx=τ⋅l∫0τBx⋅l⋅dx=τ⋅lΦ
KaTeX parse error: {align*} can be used only in display mode.
KaTeX parse error: {align*} can be used only in display mode.
KaTeX parse error: {align*} can be used only in display mode.
直流电机的电势常数
结论:
KaTeX parse error: {align*} can be used only in display mode.
电磁转矩
导体电磁力 f x = B x ⋅ l ⋅ i f_x = B_x \cdot l \cdot i fx=Bx⋅l⋅i
磁场不均匀,各导体电磁力不同;用平均磁密进行计算。
f x = B x ⋅ l ⋅ i f_x = B_x \cdot l \cdot i fx=Bx⋅l⋅i
电枢绕组总电流为 I a ,电极外径为 D a I_a,电极外径为D_a Ia,电极外径为Da
每条支路电流 i = I a 2 a i = \frac{I_a}{2a} i=2aIa
一根导体产生的电磁转矩 T x = f x ⋅ D a 2 = B x ⋅ l ⋅ i ⋅ π D a 2 π = 2 p ⋅ τ 2 π ⋅ l ⋅ I a 2 a ⋅ B x T_x = f_x \cdot \frac{D_a}{2} = B_x \cdot l \cdot i \cdot \frac{\pi D_a}{2\pi} = \frac{2p \cdot \tau }{2\pi} \cdot l \cdot \frac{I_a}{2a}\cdot B_x Tx=fx⋅2Da=Bx⋅l⋅i⋅2ππDa=2π2p⋅τ⋅l⋅2aIa⋅Bx
电磁转矩 T e m = ∑ x = 1 N a T x = 2 p ⋅ τ 2 π ⋅ l ⋅ I a 2 a ∑ x = 1 N a B x T_{em} = \sum_{x=1}^{N_a} T_x = \frac{2p \cdot \tau}{2\pi} \cdot l \cdot \frac{I_a}{2a} \sum_{x=1}^{N_a} B_x Tem=∑x=1NaTx=2π2p⋅τ⋅l⋅2aIa∑x=1NaBx
平均磁密 B a v = ∑ x = 1 N a B x N a = ∫ 0 τ B x ⋅ d x τ = ∫ 0 τ B x ⋅ l ⋅ d x τ ⋅ l = Φ τ ⋅ l B_{av} = \frac{\sum_{x=1}^{N_a} B_x}{N_a} = \frac{\int_0^\tau B_x \cdot dx}{\tau} = \frac{\int_0^\tau B_x \cdot l \cdot dx}{\tau \cdot l} = \frac{\Phi}{\tau \cdot l} Bav=Na∑x=1NaBx=τ∫0τBx⋅dx=τ⋅l∫0τBx⋅l⋅dx=τ⋅lΦ
电枢绕组产生的电磁转矩
电磁转矩公式:
T e m = p N 2 π a ⋅ Φ ⋅ I a = C T ⋅ Φ ⋅ I a T_{em} = \frac{pN}{2\pi a} \cdot \Phi \cdot I_a = C_T \cdot \Phi \cdot I_a Tem=2πapN⋅Φ⋅Ia=CT⋅Φ⋅Ia
电机的转矩常数:
C T = p N 2 π a C_T = \frac{pN}{2\pi a} CT=2πapN
结论:
(1) 电磁转矩与每极磁通 ( Φ \Phi Φ) 和电枢电流 ( I a I_a Ia) 成正比,与磁密分布无关: T M ∝ Φ ⋅ I a T_M \propto \Phi \cdot I_a TM∝Φ⋅Ia
(2) 性质:
- 发电机产生制动(反抗)转矩(与转速方向相反),吸收机械能。
- 电动机产生驱动(主)转矩(与转速方向相同),输出机械能。
(3) 改变电动机转矩的方法包括改变磁通方向或改变电枢电流方向。