title: 基数排序
date: 2024-7-25 14:29:53 +0800
categories:
- 排序算法
tags: - 排序
- 算法
- 基数排序
description: 基数排序(radix sort)的核心思想与计数排序一致,也通过统计个数来实现排序。在此基础上,基数排序利用数字各位之间的递进关系,依次对每一位进行排序,从而得到最终的排序结果。
math: true
基数排序
基数排序(Radix Sort)是一种非比较型整数排序算法。它通过将整数按位数分组排序,从最低有效位到最高有效位,或者从最高有效位到最低有效位,依次进行排序,从而实现最终的排序结果。
基数排序的原理
基数排序是一种稳定的排序算法,适用于整数排序。其主要思想是将整数按位数分组,从最低有效位开始,一次对每个位数进行计数排序(Counting Sort),最终得到有序数组。
两种实现方式
- LSD(Least Significant Digit):从最低有效位开始排序,逐步向最高有效位进行。
- MSD(Most Significant Digit):从最高有效位开始排序,逐步向最低有效位进行。
图示

基数排序的步骤
- 确定最大位数:找到数组中最大数的位数,以确定需要进行几轮排序。
- 逐位排序:从最低有效位开始,对每个位进行计数排序。
- 合并结果:每次排序完成后,合并结果进行下一轮排序,直到所有位数排序完成。
示例
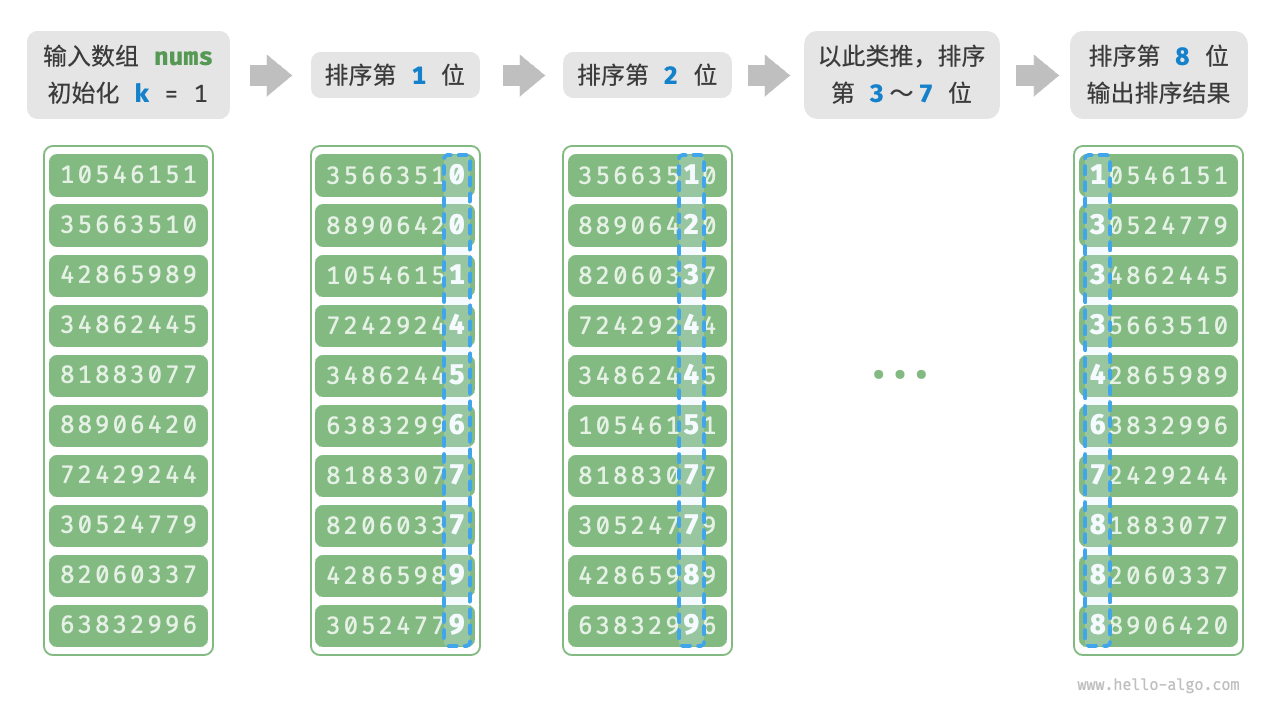
为什么从最低位开始排序?
在连续的排序轮次中,后一轮排序会覆盖前一轮排序的结果。举例来说,如果第一轮排序结果 a < b ,而第二轮排序结果 a > b,那么第二轮的结果将取代第一轮的结果。由于数字的高位优先级高于低位,因此应该先排序低位再排序高位。复杂度分析
相较于计数排序,基数排序适用于数值范围较大的情况,但前提是数据必须可以表示为固定位数的格式,且位数不能过大 。例如,浮点数不适合使用基数排序,因为其位数 k k k 过大,可能导致时间复杂度 O ( n k ) ≫ O ( n 2 ) O(nk) \gg O(n^2) O(nk)≫O(n2) 。
-
时间复杂度为 O ( n k ) O(nk) O(nk)、非自适应排序 :设数据量为 n n n、数据为 d d d 进制、最大位数为 k k k ,则对某一位执行计数排序使用 O ( n + d ) O(n + d) O(n+d) 时间,排序所有 k k k 位使用 O ( ( n + d ) k ) O((n + d)k) O((n+d)k) 时间。通常情况下, d d d 和 k k k 都相对较小,时间复杂度趋向 O ( n ) O(n) O(n) 。
-
空间复杂度为 O ( n + k ) O(n + k) O(n+k)、非原地排序 :与计数排序相同,基数排序需要借助长度为 n n n 和 k k k 的数组
res和counter。 -
稳定排序:当计数排序稳定时,基数排序也稳定;当计数排序不稳定时,基数排序无法保证得到正确的排序结果。
时间复杂度
- 最佳情况 : O ( n k ) O(nk) O(nk)
- 最坏情况 : O ( n k ) O(nk) O(nk)
- 平均情况 : O ( n k ) O(nk) O(nk)
空间复杂度
- 空间复杂度 : O ( n + k ) O(n + k) O(n+k)。
Java代码实现
对于一个 d d d 进制的数字 x x x ,要获取其第 k k k 位 x k x_k xk ,可以使用以下计算公式:
x k = ⌊ x d k − 1 ⌋ m o d d x_k = \lfloor\frac{x}{d^{k-1}}\rfloor \bmod d xk=⌊dk−1x⌋modd
其中 ⌊ a ⌋ \lfloor a \rfloor ⌊a⌋ 表示对浮点数 a a a 向下取整,而 m o d d \bmod \: d modd 表示对 d d d 取模(取余)。
比如8位10进制的数据, d = 10 d = 10 d=10 且 k ∈ [ 1 , 8 ] k \in [1, 8] k∈[1,8] 。
此外,我们需要小幅改动计数排序代码,使之可以根据数字的第 k k k 位进行排序:
java
/* 获取元素 num 的第 k 位,其中 exp = 10^(k-1) */
int digit(int num, int exp) {
// 传入 exp 而非 k 可以避免在此重复执行昂贵的次方计算
return (num / exp) % 10;
}
/* 计数排序(根据 nums 第 k 位排序) */
void countingSortDigit(int[] nums, int exp) {
// 十进制的位范围为 0~9 ,因此需要长度为 10 的桶数组
int[] counter = new int[10];
int n = nums.length;
// 统计 0~9 各数字的出现次数
for (int i = 0; i < n; i++) {
int d = digit(nums[i], exp); // 获取 nums[i] 第 k 位,记为 d
counter[d]++; // 统计数字 d 的出现次数
}
// 求前缀和,将"出现个数"转换为"数组索引"
for (int i = 1; i < 10; i++) {
counter[i] += counter[i - 1];
}
// 倒序遍历,根据桶内统计结果,将各元素填入 res
int[] res = new int[n];
for (int i = n - 1; i >= 0; i--) {
int d = digit(nums[i], exp);
int j = counter[d] - 1; // 获取 d 在数组中的索引 j
res[j] = nums[i]; // 将当前元素填入索引 j
counter[d]--; // 将 d 的数量减 1
}
// 使用结果覆盖原数组 nums
for (int i = 0; i < n; i++)
nums[i] = res[i];
}
/* 基数排序 */
void radixSort(int[] nums) {
// 获取数组的最大元素,用于判断最大位数
int m = Integer.MIN_VALUE;
for (int num : nums)
if (num > m)
m = num;
// 按照从低位到高位的顺序遍历
for (int exp = 1; exp <= m; exp *= 10) {
// 对数组元素的第 k 位执行计数排序
// k = 1 -> exp = 1
// k = 2 -> exp = 10
// 即 exp = 10^(k-1)
countingSortDigit(nums, exp);
}
}