文章目录
- 1、知识回顾
- 2、Self-attetion实现步骤
- 3、准备输入
- 4、初始化参数
- 5、获取Q,K,V
- [6、计算attention scores](#6、计算attention scores)
- 7、计算softmax
- 8、给values乘上scores
- 9、完整代码
- 10、总结
🍃作者介绍:双非本科大四网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法,初步涉猎人工智能和前端开发。
🦅个人主页:@逐梦苍穹
📕所属专栏:人工智能
🌻gitee地址:xzl的人工智能代码仓库
✈ 您的一键三连,是我创作的最大动力🌹
1、知识回顾
关于Self-Attention的一系列理论知识,请看我的另外一篇文章:
深入剖析Self-Attention自注意力机制【图解】:https://xzl-tech.blog.csdn.net/article/details/141308634
这篇文章讲到了self-attention的计算过程,如果不想看那么细致的话,我们还是在这里简单复习一下:
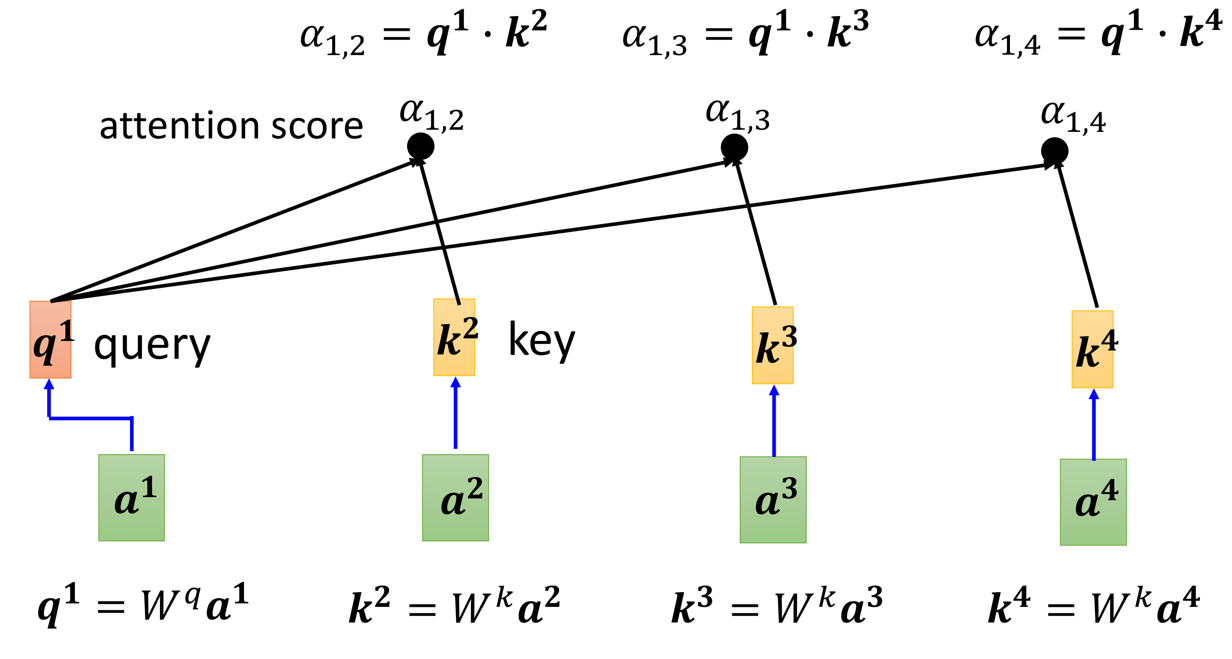
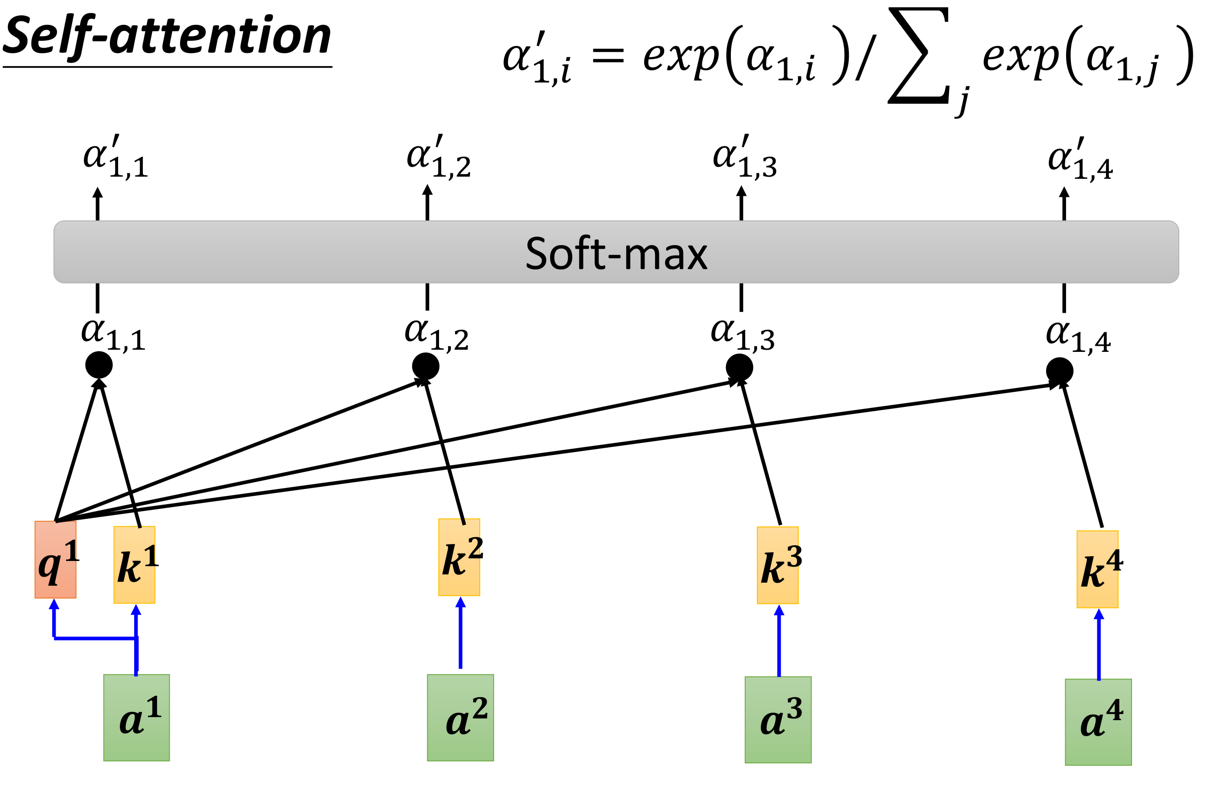
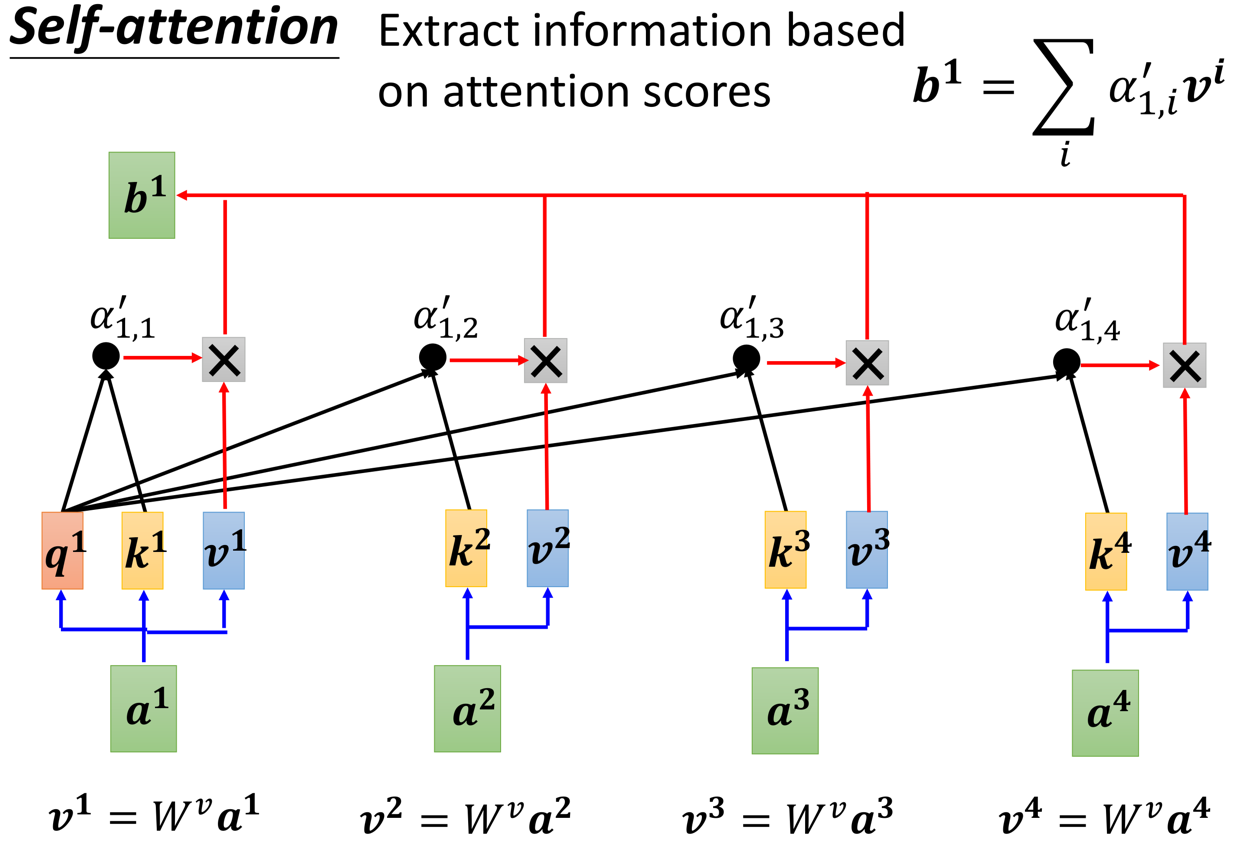
那么,需要告诉大家的是,既然是要用代码实现,那肯定是需要以一个矩阵的角度去看待整个self-attention的计算过程,请看下文!
2、Self-attetion实现步骤
这里我们实现的注意力机制是现在比较流行的点积相乘的注意力机制
self-attention机制的实现步骤:
- 准备输入
- 初始化参数
- 获取key,query和value
- 给input1计算attention score
- 计算softmax
- 给value乘上score,获得output
整个过程都是以矩阵的视角在操作的:

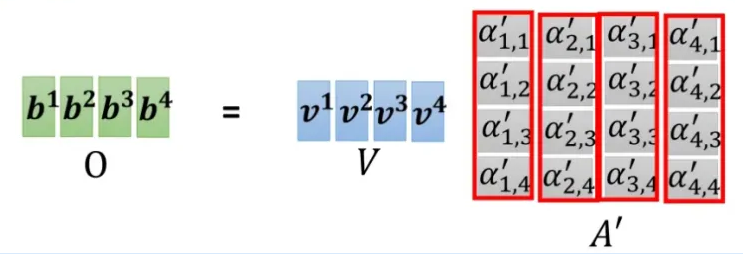
3、准备输入
本文的关注点在于实现过程,所以数据方面我们采用自定义的方式获取:
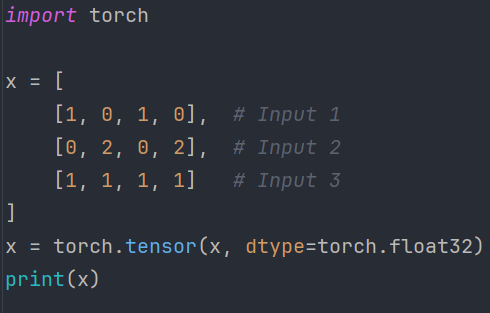
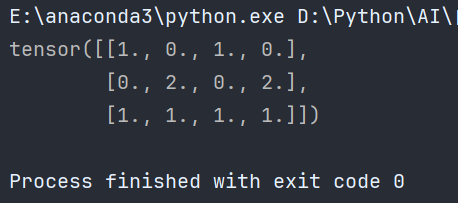
这样就会得到如下张量:
4、初始化参数
在我上一篇剖析self-attention机制的文章中提到,整个self-attention的计算过程,需要学习的只有三个参数,那就是q,k,v对应的权重矩阵:
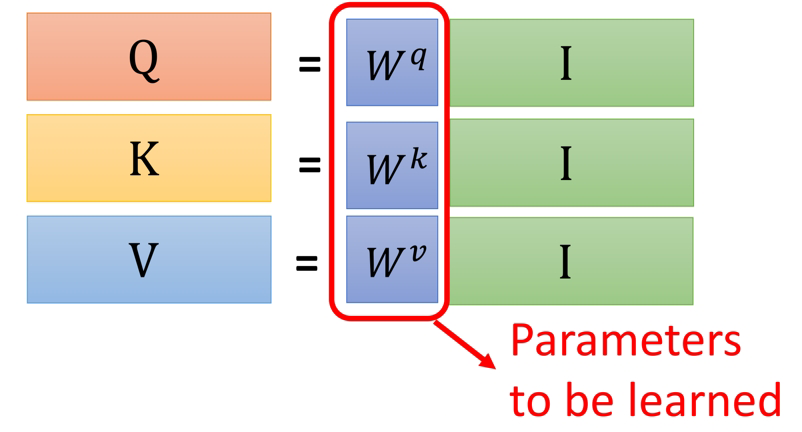
这里同样不细讲如何学习,这里的重点在于带大家跑通整个self-attention计算的代码流程,
所以初始化参数如下:
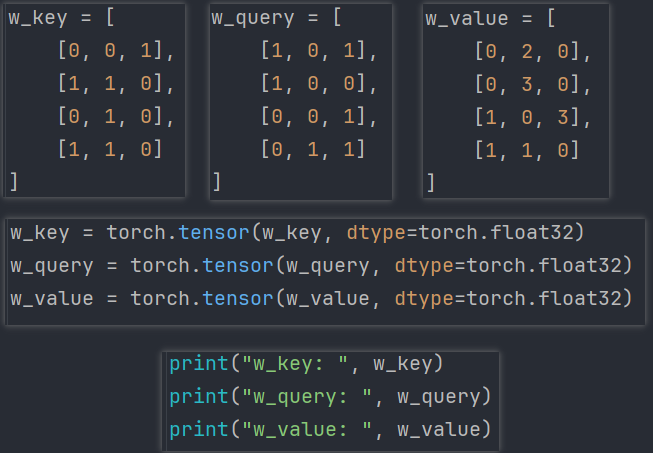
来看一下输出:
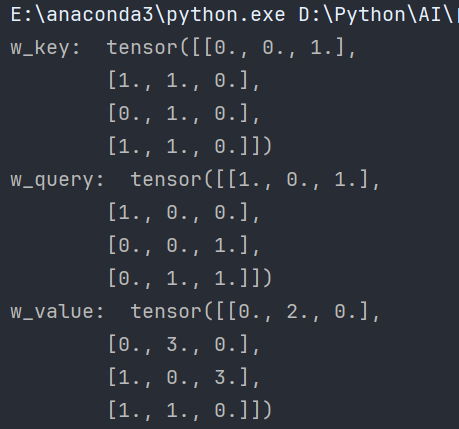
5、获取Q,K,V
前面初始化了q,k,v对应的权重矩阵,下面获取Q,K,V:
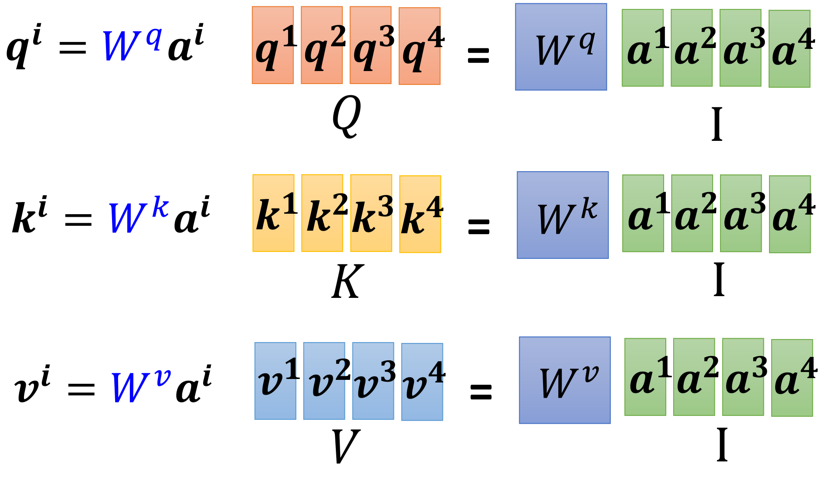
如图所示,我们可以得到如下表达式:
Q = W q ( I n p u t ) Q=W^q(Input) Q=Wq(Input)
K = W k ( I n p u t ) K=W^k (Input) K=Wk(Input)
V = W v ( I n p u t ) V=W^v (Input) V=Wv(Input)
代码实现:

得到结果:
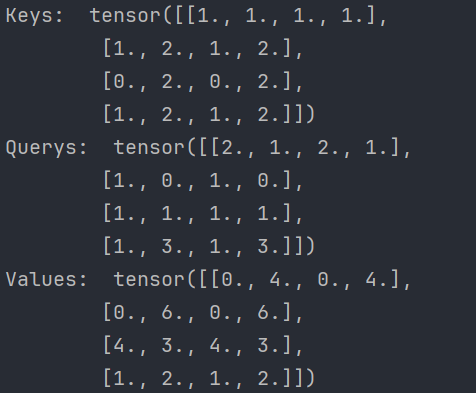
6、计算attention scores
我在上一篇讲解self-attention机制的文章中,关于计算attention scores的过程其实是分步计算的:
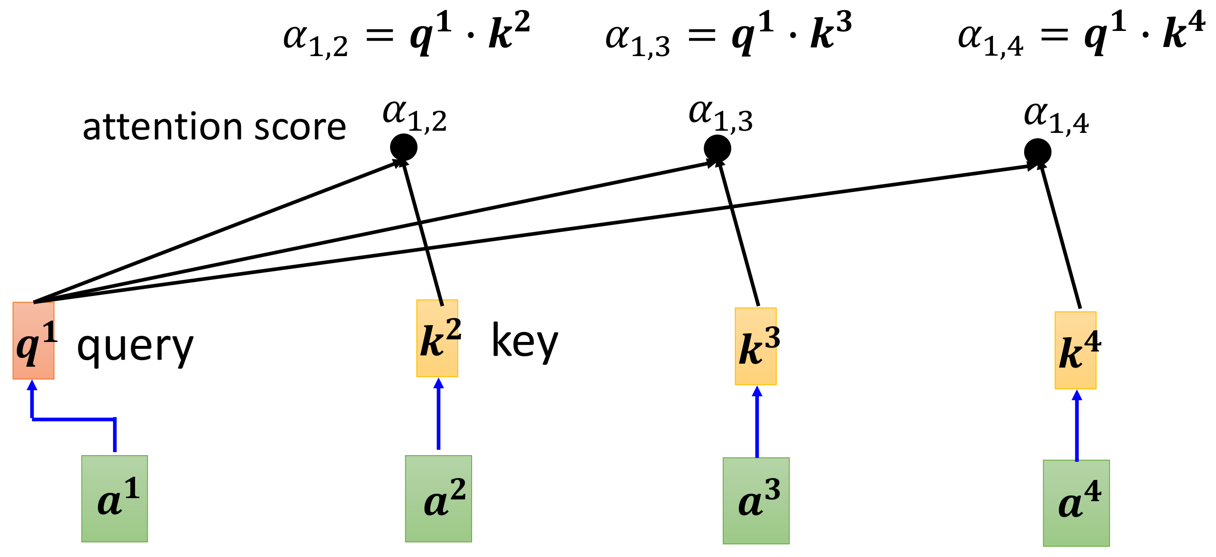
即分步计算 α i , j \alpha_{i,j} αi,j
但是在代码实现上,我们上面已经全部矩阵化了,我们得到的不是单独的 K 1 K^1 K1或者是 K 2 K^2 K2,而是关于 K a l l K^{all} Kall的矩阵( Q a l l Q^{all} Qall和 V a l l V^{all} Vall同理):
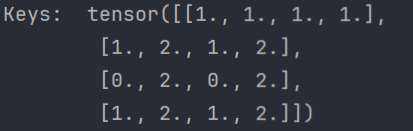
画成图解就是:
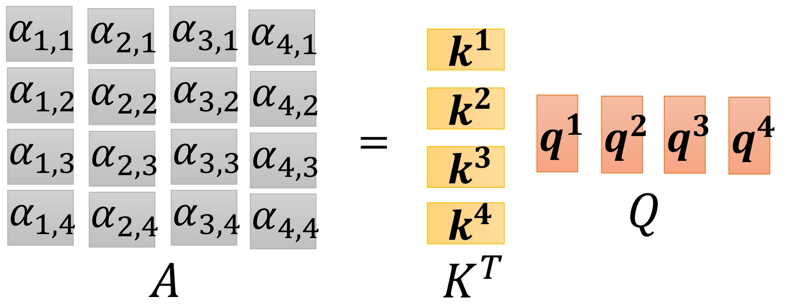
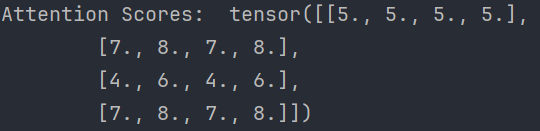
所以这里计算的attention scores 用代码表示就是:

输出效果:
7、计算softmax
同样,这里一口气将所有的 α i , j \alpha_{i,j} αi,j经过 S o f t m a x Softmax Softmax处理:

代码:

输出:

代码里面的dim=-1,指定在最后一个维度上应用 softmax 操作;
在二维张量的情况下,
dim=-1指的是在每一行(行向量)上计算 softmax
8、给values乘上scores
使用经过softmax后的attention score乘以它对应的value值:
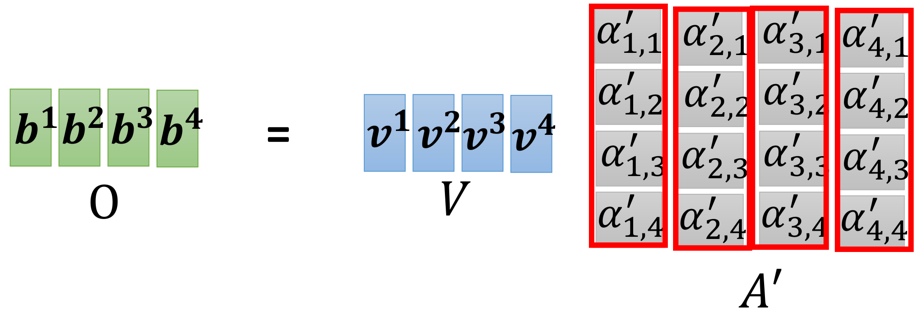
代码:

输出:
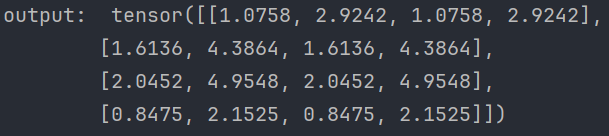
9、完整代码
完整代码,代码即注释:
python
# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/8/19 17:24
import torch
from torch.nn.functional import softmax
# 输入数据 x,包含3个输入向量,每个向量有4个维度
x = [
[1, 0, 1, 0], # 输入向量1
[0, 2, 0, 2], # 输入向量2
[1, 1, 1, 1] # 输入向量3
]
# 将输入数据转换为 PyTorch 张量,并设置数据类型为 float32
x = torch.tensor(x, dtype=torch.float32)
# 定义键(Key)的权重矩阵,形状为 (4, 3)
w_key = [
[0, 0, 1],
[1, 1, 0],
[0, 1, 0],
[1, 1, 0]
]
# 定义查询(Query)的权重矩阵,形状为 (4, 3)
w_query = [
[1, 0, 1],
[1, 0, 0],
[0, 0, 1],
[0, 1, 1]
]
# 定义值(Value)的权重矩阵,形状为 (4, 3)
w_value = [
[0, 2, 0],
[0, 3, 0],
[1, 0, 3],
[1, 1, 0]
]
# 将权重矩阵转换为 PyTorch 张量,并设置数据类型为 float32
w_key = torch.tensor(w_key, dtype=torch.float32)
w_query = torch.tensor(w_query, dtype=torch.float32)
w_value = torch.tensor(w_value, dtype=torch.float32)
# 打印权重矩阵以供检查
print("w_key: ", w_key)
print("w_query: ", w_query)
print("w_value: ", w_value)
# 计算 Keys: 将输入 x 与键的权重矩阵相乘,生成键向量
keys = w_key @ x
# 计算 Queries: 将输入 x 与查询的权重矩阵相乘,生成查询向量
querys = w_query @ x
# 计算 Values: 将输入 x 与值的权重矩阵相乘,生成值向量
values = w_value @ x
# 打印键、查询和值向量以供检查
print("Keys: ", keys)
print("Querys: ", querys)
print("Values: ", values)
# 计算注意力分数(Attention Scores):通过键和查询向量的点积计算
# 结果是一个 (4, 4) 的矩阵,其中每个元素表示查询和键之间的相似度
attn_scores = keys @ querys
print("Attention Scores: ", attn_scores)
# 对注意力分数应用 Softmax 函数,将其转换为概率分布
# Softmax 处理后的矩阵形状仍为 (4, 4),表示每个查询对所有键的关注度
attn_scores_softmax = softmax(attn_scores, dim=-1)
print("Attention Scores Softmax: ", attn_scores_softmax)
# 计算加权后的输出值:将值向量与注意力分数进行加权求和
# 结果是一个形状为 (4, 4) 的矩阵,表示经过注意力加权后的最终输出
output = values @ attn_scores_softmax
print("output: ", output)10、总结
对全文的代码过程做一个总结:
这份代码实现了自注意力机制的核心部分,包括键 (Key)、查询 (Query)和值 (Value)的计算,以及通过注意力分数进行加权求和的过程
- 输入与权重定义
- 输入数据
x包含 3 个向量,每个向量有 4 个维度 - 定义了三个权重矩阵
w_key、w_query和w_value,分别用于生成键、查询和值向量。
- 输入数据
- 计算键、查询和值向量
- 将输入
x分别与w_key、w_query和w_value相乘,生成对应的键、查询和值向量 - 这个步骤是将输入映射到不同的特征空间,以便进行注意力计算
- 将输入
- 计算注意力分数
- 通过键向量和查询向量的点积计算注意力分数
- 这些分数表示查询向量与键向量之间的相似度,用于决定每个查询向量对不同键向量的关注程度
- 应用 Softmax 函数
- 对注意力分数进行
softmax操作,将这些分数转换为概率分布,确保每个查询对所有键的注意力之和为 1 - 这一步将注意力分数变为实际的注意力权重
- 对注意力分数进行
- 计算加权后的输出值
- 将值向量与注意力权重相乘并求和,得到最终的加权输出
- 这一步模拟了注意力机制如何根据注意力权重聚合输入信息,从而生成最终的上下文表示
这些代码完整地展示了自注意力机制的基本工作流程;
通过计算注意力分数并对值向量进行加权求和,自注意力机制能够在输入序列中捕捉到相关信息,从而在各种深度学习任务中生成更具上下文感知的输出。