letcode 分类练习 110. 平衡二叉树 257. 二叉树的所有路径 404. 左叶子之和 222. 完全二叉树的节点个数

letcode 分类练习 110. 平衡二叉树 101. 对称二叉树 104.二叉树的最大深度 111.二叉树的最小深度

[110. 平衡二叉树](#110. 平衡二叉树)
[257. 二叉树的所有路径](#257. 二叉树的所有路径)
[404. 左叶子之和](#404. 左叶子之和)
[222. 完全二叉树的节点个数](#222. 完全二叉树的节点个数)

对称二叉树 104.二叉树的最大深度 111.二叉树的最小深度)

110. 平衡二叉树

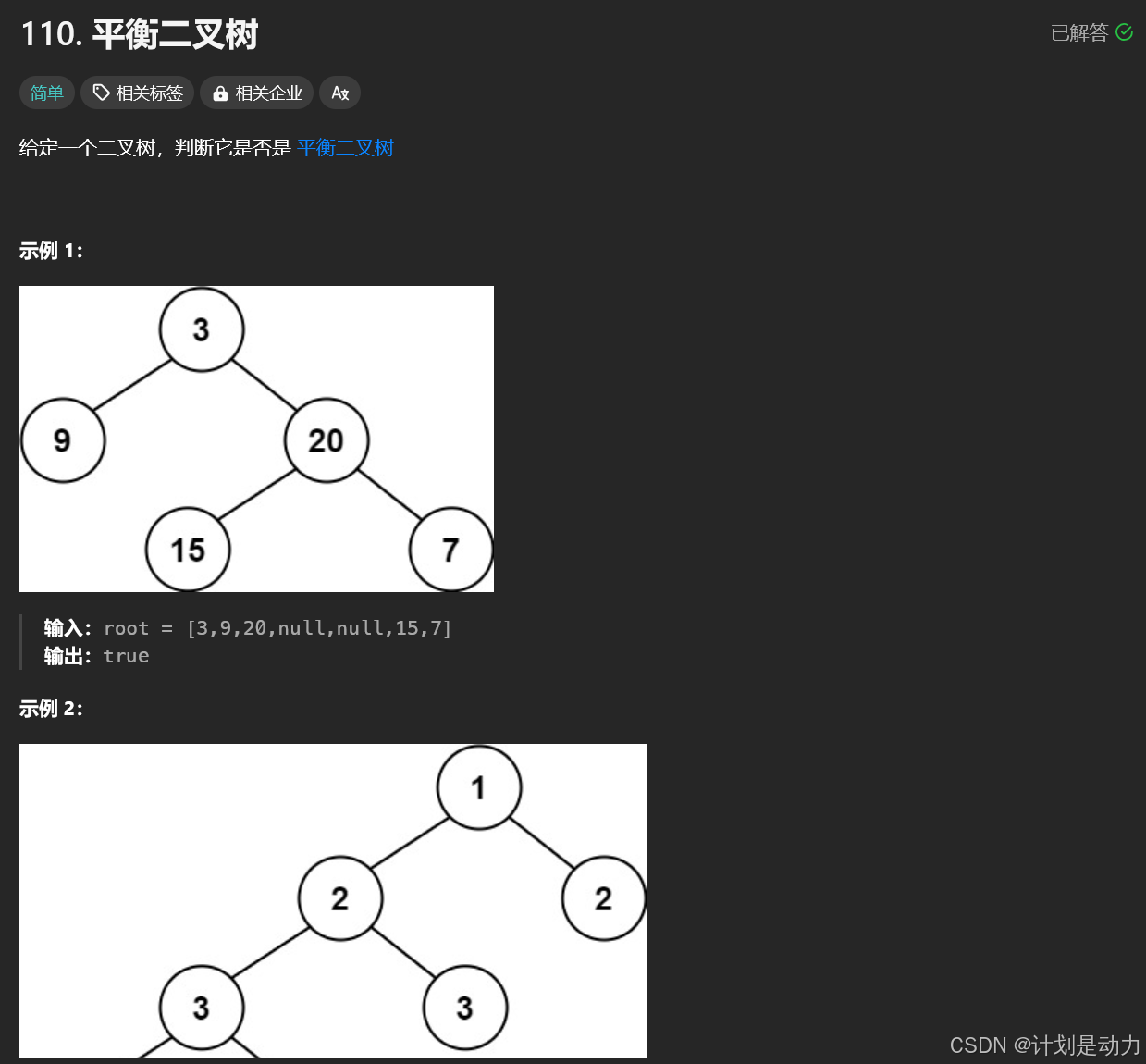
用递归的思路检查左子树和右子树的高度差绝对值是不是在1以内,为了方便同时获取左子树和右子树的高度，我们定义如果高度为-1表示该子树不满足平衡二叉树，如果不等于-1表示子树的高度

c 复制代码

class Solution {
public:
    int height(TreeNode* node){
        if(!node) return 0;
        int left_depth = height(node -> left);
        int right_depth = height(node -> right);
        if(left_depth == -1 || right_depth == -1 || abs(left_depth - right_depth) > 1)return -1;
        else return max(left_depth, right_depth) + 1;
    }
    bool isBalanced(TreeNode* root) {
        return height(root) >= 0;
    }
};

257. 二叉树的所有路径

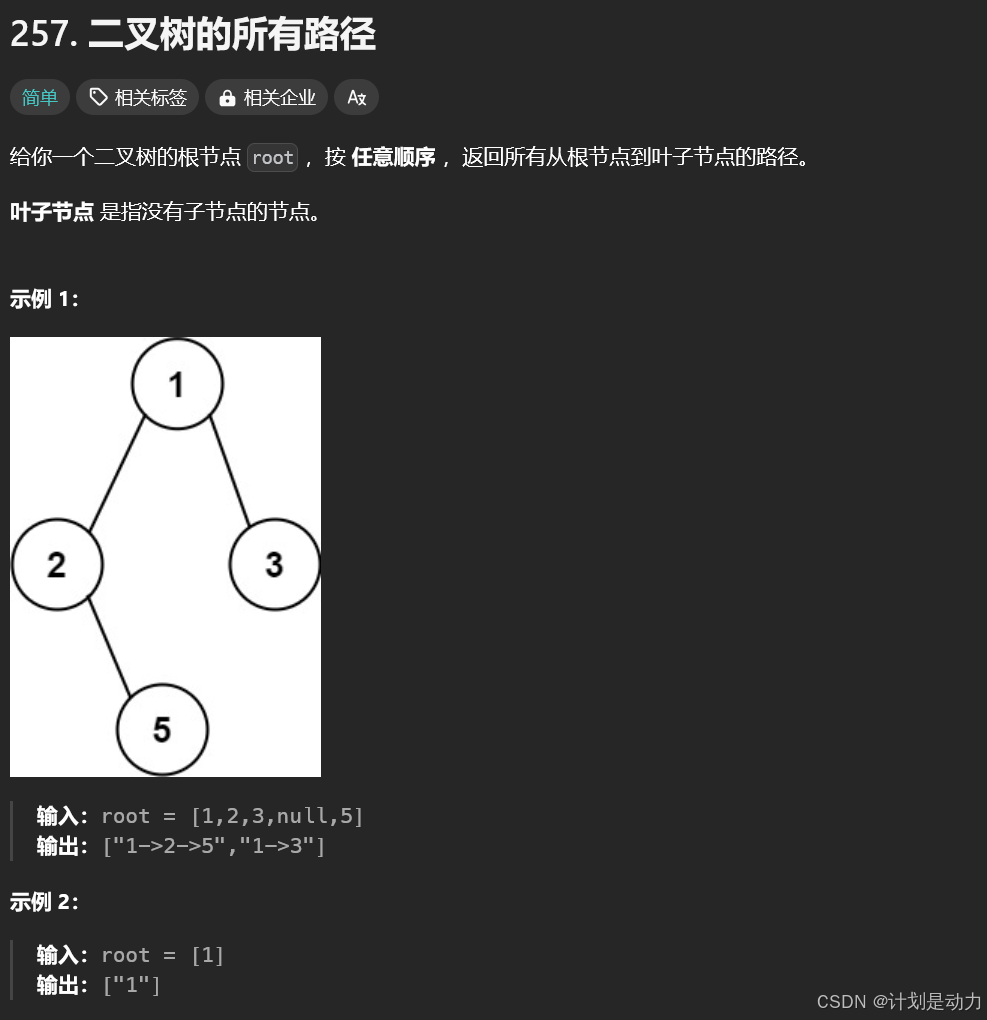
每个节点都对应唯一的从根节点出发的路径，只需要做一个遍历，如果它是叶子节点就记录路径即可

c 复制代码

class Solution {
public:
    vector<string> result;
    void dfs(TreeNode* root, string s){
        if(!root) return;
        if(!root->left && !root->right)result.push_back(s);
        if(root->left)dfs(root -> left, s + "->" + to_string(root -> left -> val));
        if(root->right)dfs(root -> right, s + "->" + to_string(root -> right -> val));
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        if(!root) return result;
        if(!root -> left&& !root->right){result.push_back(to_string(root->val)); return result;}
        dfs(root, to_string(root->val));
        return result;
    }
};

404. 左叶子之和

传参的时候可以告诉该节点是左孩子还是右孩子，再判断一下当前节点是不是叶子结点即可

c 复制代码

class Solution {
public:
    int sum = 0;
    void dfs(TreeNode* root, int flag){
        if(!root) return;
        if(!root -> left && !root -> right && flag == 0)sum+= root->val;
        dfs(root->left, 0);
        dfs(root ->right, 1);
    }
    int sumOfLeftLeaves(TreeNode* root) {
        dfs(root, -1);
        return sum;
    }
};

222. 完全二叉树的节点个数

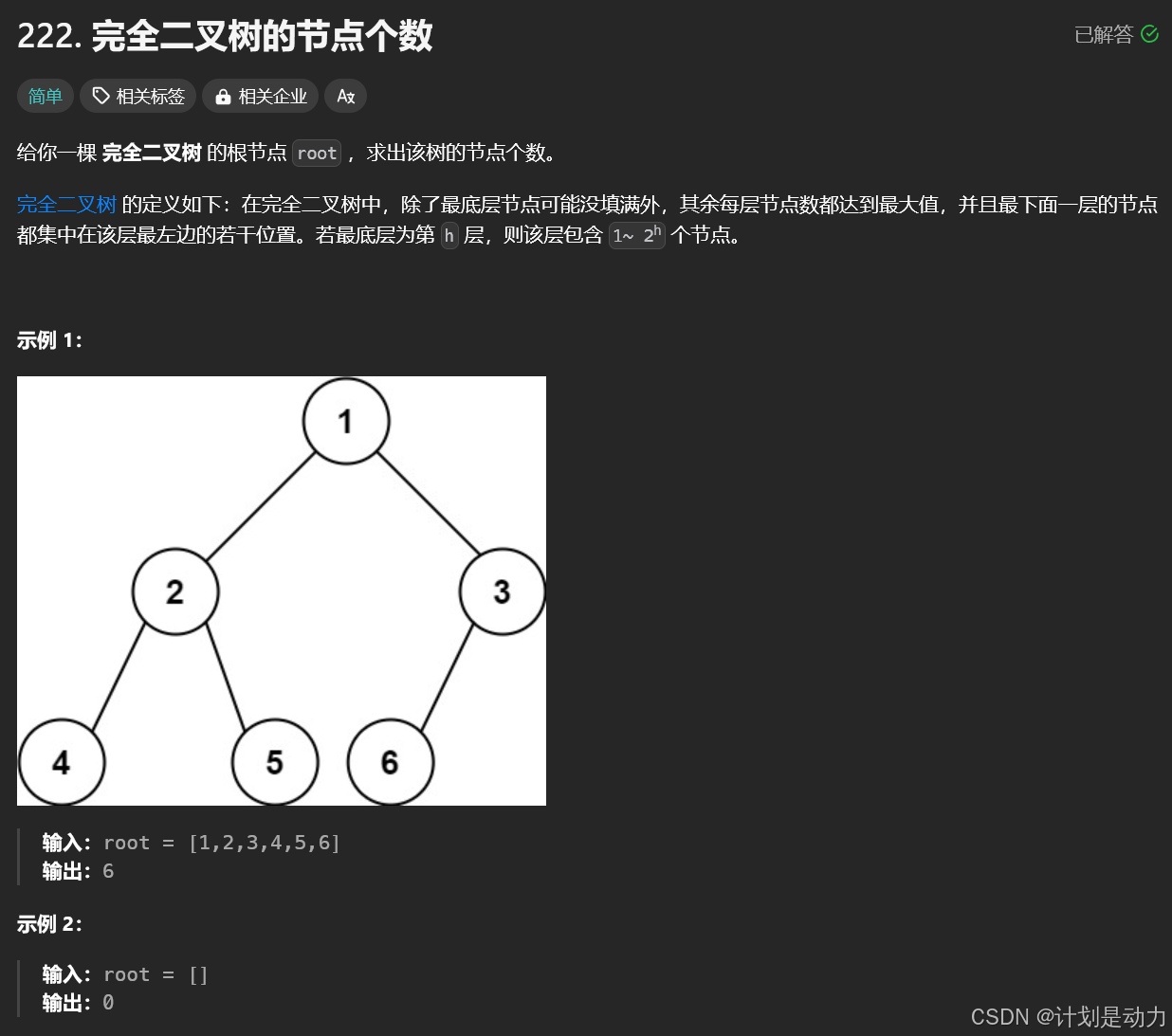
可以利用完全二叉树的性质解题

完全二叉树是一定要按照一层一层的顺序装填的，所以判断完全二叉树只需要一直向左和一直向右迭代，两边的深度一样即可，注意下面的不是完全二叉树：

c 复制代码

class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr) return 0;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
        while (left) {  // 求左子树深度
            left = left->left;
            leftDepth++;
        }
        while (right) { // 求右子树深度
            right = right->right;
            rightDepth++;
        }
        if (leftDepth == rightDepth) {
            return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0
        }
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};