代码随想录算法训练营第二十三天（回溯 二）

力扣题部分:

39. 组合总和

题目链接:. - 力扣（LeetCode）

题面:

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

思路:

记得昨天的组合吗？

这道题和那道题最大的差别就是一个数能不能重复多次选取。

传送门:代码随想录算法训练营第二十二天（回溯 一）-CSDN博客

如果那道题看懂了，这道题唯一的难点就是一个数能重复用代码上是怎么体现的，

可能会有人觉得这一点就会让代码差别巨大，这样的想法其实没什么问题，但是对于这道题，改的其实不多，添一个sum的求和我就不多讲了，下面的代码中最值得注意的还是调用递归那行：

fun(candidates, target, sum, i);

如果你对组合的代码还有印象，那应该记得组合的代码递归时i应该是i + 1才对。

如果递归从i开始，进入递归函数后之前的i变成index，在新的函数中又从index开始，那是不是就可以一直重复了呢？相反，i+1意味着递归的i只能从原来i（index）的下一个开始遍历。

理解完这个点和组合代码的来龙去脉，打出下面的代码就没什么问题了。

代码实现:

class Solution {
public:
    vector<int> rightnums;
    vector<vector<int>> ressult;
    void fun(vector<int> candidates, int target, int sum, int index)
    {
        if(sum == target)
        {
            ressult.push_back(rightnums);
            return;
        }
        if(sum > target) return;
        for(int i = index;i < candidates.size();i ++)
        {
            sum += candidates[i];
            rightnums.push_back(candidates[i]);
            fun(candidates, target, sum, i);
            sum -= candidates[i];
            rightnums.pop_back();
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        fun(candidates,target,0, 0);
        return ressult;
    }
};

40.组合总和II

题目链接:. - 力扣（LeetCode）

题面:

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

**注意：**解集不能包含重复的组合。

思路:

虽然又改动了一些，这次的应对就相对前一道题麻烦不少。

因为数字可以有多个相同的，按照原来的代码，这会造成一个问题， 下面我们举个例子：

示例 1:

candidates = [10,1,2,7,6,1,5], target = 8,

很明显，因为有两个1，我们会得到两个{1，7}。

有人可能会说，将原来数组去掉重复的1不就好了？

如果去掉了两个1中的任何一个，我们又会少掉{1，1，6}这个答案。

看来没什么投机取巧的简单改动了，所以这里选择的是用一个bool类型的数组记录各元素使用情况，不仅如此，为了让同样的元素在一块，我们还要排序，排好之后怎么去重呢？下面的一行代码可以解决去重问题，我先呈现代码，再做解释：

if(i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) continue;

这行代码其实挺难解释的， 如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。

此时for循环里就应该做continue的操作。

这块比较抽象，代码随想录弄了一个图解，

这里为了让图弄得不会太复杂，换一个简单一点的例子

candidates = [1, 1, 2], target = 3，（candidates已经排序，相同元素在一起）

我在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：

• used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
• used[i - 1] == false，说明同一树层candidates[i - 1]使用过

可能有的录友想，为什么 used[i - 1] == false 就是同一树层呢，因为同一树层，used[i - 1] == false 才能表示，当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。

而 used[i - 1] == true，说明是进入下一层递归，去下一个数，所以是树枝上，如图所示：

这块去重的逻辑很抽象，希望大家多理解记忆吧。

代码实现:

class Solution {
public:
    vector<int> rightnums;
    vector<vector<int>> result;
    void fun(vector<int>candidates, int target, int sum, int index, vector<bool> &used)
    {
        if(sum > target) return;
        if(sum == target)
        {

            result.push_back(rightnums);
            return;
        }
        for(int i = index; i < candidates.size(); i ++)
        {
            if(i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) continue;
            sum += candidates[i];
            rightnums.push_back(candidates[i]);
            used[i] = true;
            fun(candidates, target, sum, i + 1, used);
            rightnums.pop_back();
            sum -= candidates[i];
            used[i] = false;
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> used(candidates.size(), false);
        sort(candidates.begin(), candidates.end());
        fun(candidates,target, 0, 0, used);
        return result;
    }
};

131.分割回文串

题目链接:. - 力扣（LeetCode）

题面:

给你一个字符串 s，请你将s分割成一些子串，使每个子串都是 回文串

（回文 串是向前和向后读都相同的字符串。）

返回 s 所有可能的分割方案。

思路:

本题这涉及到两个关键问题：

1. 切割问题，有不同的切割方式
2. 判断回文

这种题目，想用for循环暴力解法，可能都不那么容易写出来，所以要换一种暴力的方式，就是回溯。

一些同学可能想不清楚 回溯究竟是如何切割字符串呢？

我们来分析一下切割，其实切割问题类似组合问题。

例如对于字符串abcdef：

• 组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个.....。
• 切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段.....。

所以切割问题，也可以抽象为一棵树形结构，如图：

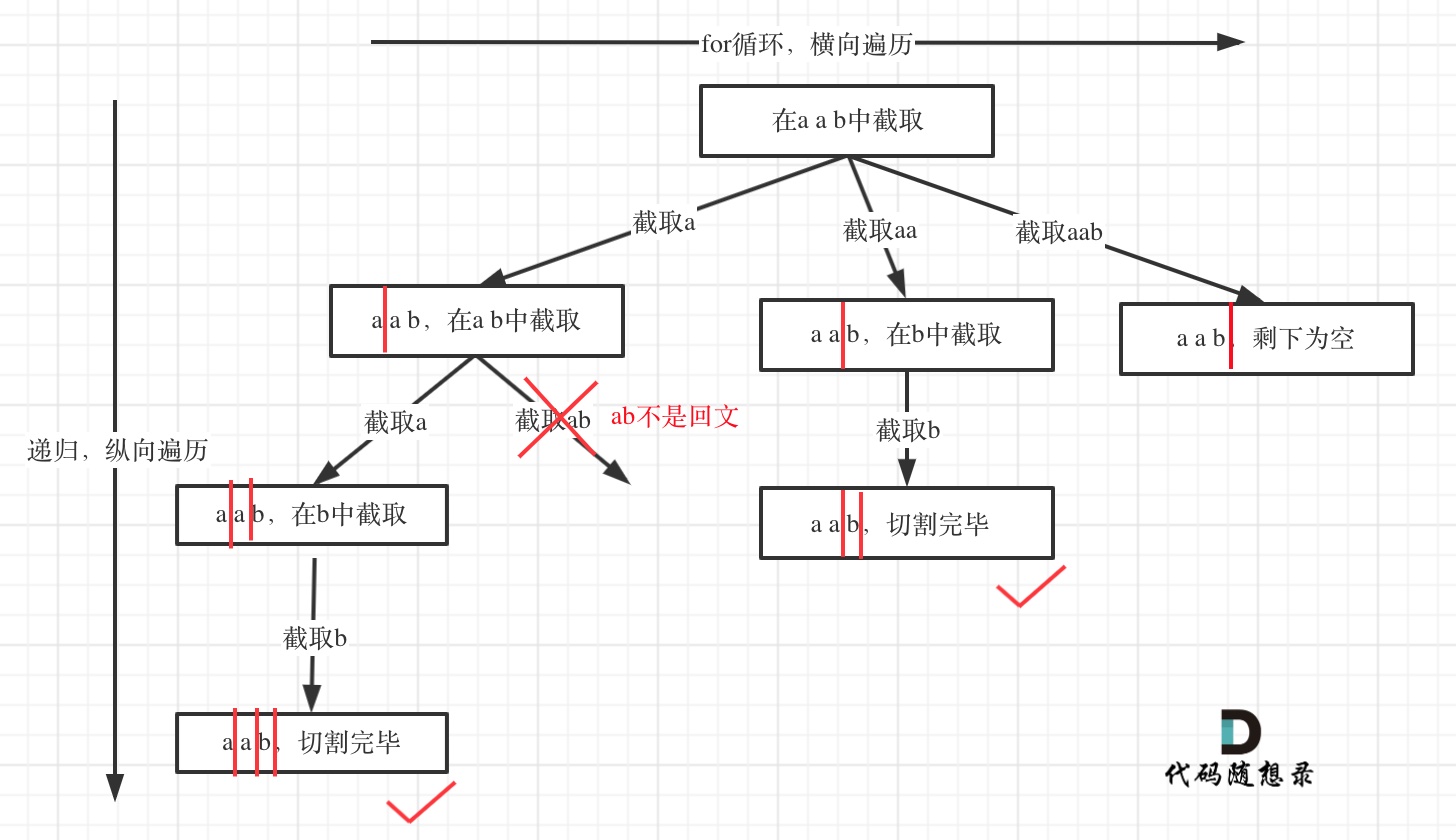
递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

那么在代码里什么是切割线呢？

在处理组合问题的时候，递归参数需要传入startIndex，表示下一轮递归遍历的起始位置，这个startIndex就是切割线，可以结合下面的判断终止条件的代码理解一下

void backtracking (const string& s, int startIndex) {
    // 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
    if (startIndex >= s.size()) {
        result.push_back(path);
        return;
    }
}

终止条件想明白了的话其实难点也差不多没了，剩下的就是for循环遍历和判断回文了，个人感觉没什么其他太多值得说的，我就直接呈现套模板的代码了。

代码实现:

class Solution {
public:
    vector<vector<string>> result;
    vector<string> right; // 放已经回文的子串
    bool judge(const string &s, int begin, int end)
    {
        int i, j;
        for(i = begin, j = end; i < j; i ++, j --)
        {
            if(s[i] != s[j]) return false;
        }
        return true;
    }
    void backtracking (const string &s, int startIndex) 
    {
        if(startIndex >= s.size())
        {
            result.push_back(right);
            return;
        }
        for(int i = startIndex; i < s.size(); i ++)
        {
            if(judge(s, startIndex, i))
            {
                string son = s.substr(startIndex,i - startIndex + 1);
                right.push_back(son);
                backtracking(s, i + 1);
                right.pop_back();
            }
        }
    }
    vector<vector<string>> partition(string s) 
    {
        backtracking(s, 0);
        return result;
    }
};