【Hot100】LeetCode—94. 二叉树的中序遍历

目录

• [1- 思路](#1- 思路)
• • 栈-统一遍历
• [2- 实现](#2- 实现)
• • [⭐94. 二叉树的中序遍历------题解思路](#⭐94. 二叉树的中序遍历——题解思路)
• [3- ACM实现](#3- ACM实现)

---

• 原题连接：94. 二叉树的中序遍历

1- 思路

栈-统一遍历

二叉树的处理遍历过程，主要分为两步

• 1- 访问节点
• 2- 处理节点

中序遍历

• 中序遍历的顺序是 ------> 左 中 右 ------> 给我们的又是根节点，需要从根节点开始访问
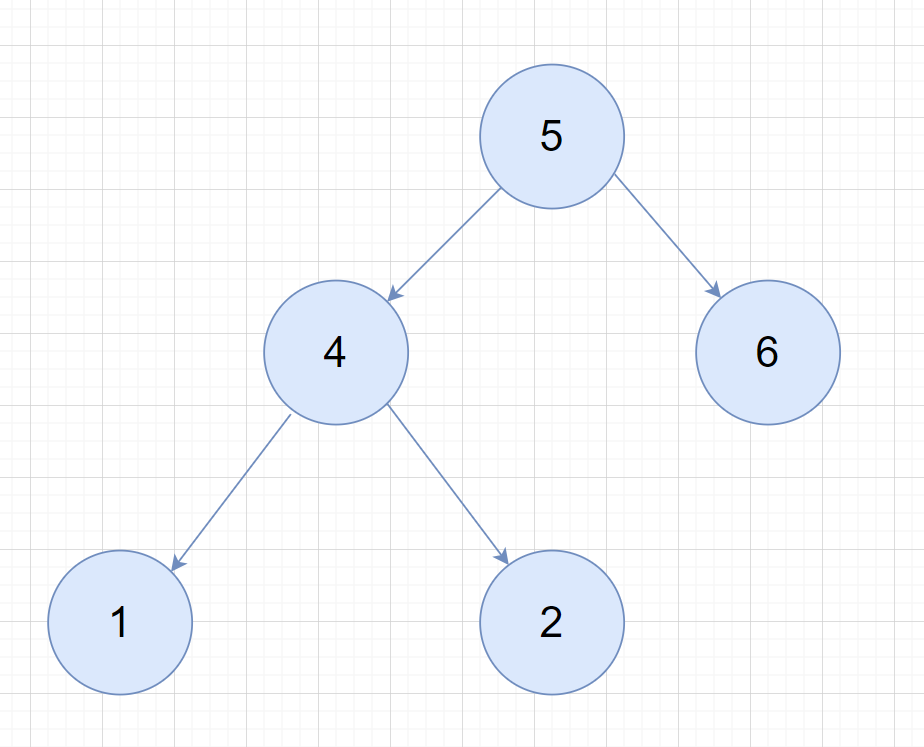
• 例如二叉树，可以看到从根节点 5 开始访问，但不能先处理节点 5
  • 先访问 5 ------> 4 ------> 1 ，其中 1 才是我们需要处理的结点。

借助栈实现

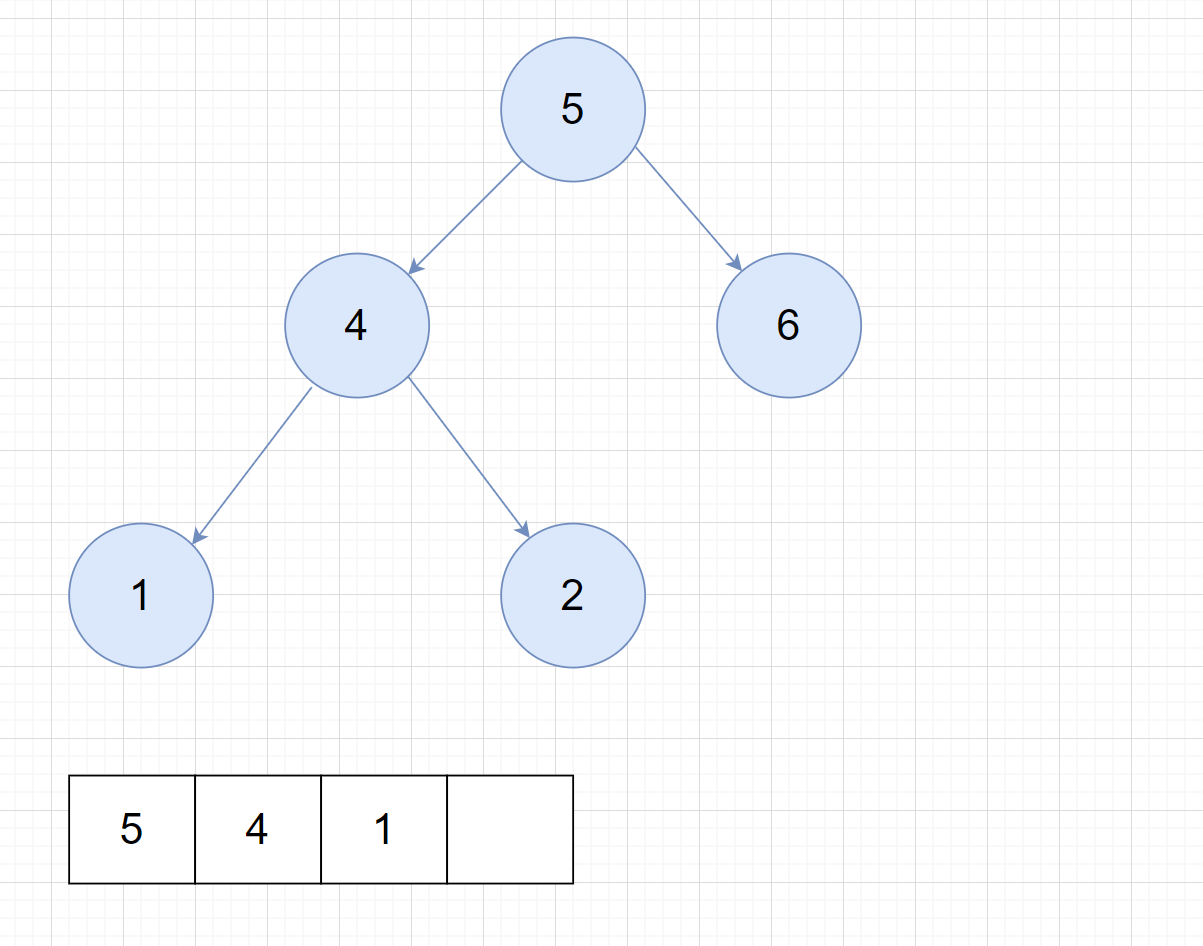
• 使用一个指针，来遍历二叉树，访问节点后将其入栈
• 直到遍历到 null，比如指针到 1 的左节点此时是 null 了，就需要栈中弹出元素，处理第一个结点就是 1 ，之后将 1 加入结果集

---

2- 实现

⭐94. 二叉树的中序遍历------题解思路

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> st = new Stack<>();
        if(root==null){
            return res;
        }

        // 指针
        TreeNode cur = root;
        while(cur!=null || !st.isEmpty()){
            if(cur!=null){
                st.push(cur);
                cur = cur.left;
            }else{
                cur = st.pop();
                res.add(cur.val);
                cur = cur.right;
            }
        }
        return res;
    }
}

---

3- ACM实现

public class inorderT {

    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode() {}
        TreeNode(int val) { this.val = val; }
        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }



    public static TreeNode build(String str){
        if(str == null || str.length()==0){
            return null;
        }
        String input = str.replace("[","");
        input = input.replace("]","");
        String[] parts = input.split(",");

        Integer[] nums = new Integer[parts.length];
        for(int i  = 0 ; i < parts.length;i++){
            if(!parts[i].equals("null")){
                nums[i] = Integer.parseInt(parts[i]);
            }else{
                nums[i] = null;
            }
        }
        Queue<TreeNode> queue = new LinkedList<>();
        TreeNode root = new TreeNode(nums[0]);
        queue.offer(root);
        int index = 1;
        while(!queue.isEmpty()&& index<parts.length){
            TreeNode node = queue.poll();
            if(index<nums.length && nums[index]!=null){
                node.left = new TreeNode(nums[index]);
                queue.offer(node.left);
            }
            index++;
            if(index<nums.length && nums[index]!=null){
                node.right = new TreeNode(nums[index]);
                queue.offer(node.right);
            }
            index++;
        }
        return root;
    }


    public static List<Integer> inorderT(TreeNode root){
        // 借助 栈 + 指针
        TreeNode cur = root;
        Stack<TreeNode> st = new Stack<>();
        List<Integer> res = new ArrayList<>();
        if(root==null){
            return res;
        }
        // 遍历
        while (cur!=null || !st.isEmpty()){
            // 一直遍历
            if(cur!=null){
                st.push(cur);
                cur = cur.left;
            }else{
                // 处理节点
                cur = st.pop();
                res.add(cur.val);
                cur = cur.right;
            }
        }
        return res;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String input = sc.nextLine();
        TreeNode root = build(input);
        List<Integer> res = inorderT(root);
        System.out.println(res.toString());
    }
}