manim边学边做--曲线类

manim中曲线，除了前面介绍的圆弧类曲线，也可以绘制任意的曲线。

manim中提供的CubicBezier模块，可以利用三次贝塞尔曲线的方式绘制任意曲线。

关于贝塞尔曲线的介绍，可以参考：https://en.wikipedia.org/wiki/Bézier_curve。

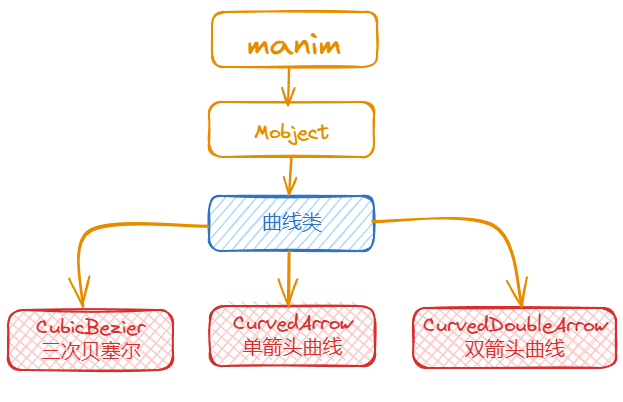
本文主要介绍贝塞尔曲线和两种带箭头的曲线的模块。

1. CubicBezier：三次贝塞尔曲线，可以绘制平面上的任意曲线
2. CurvedArrow：单箭头曲线
3. CurvedDoubleArrow：双箭头曲线

1. 主要参数

CurvedArrow和CurvedDoubleArrow的主要参数就是曲线的起点和终点，

这两个模块继承自ArcBetweenPoints模块。

参数名称	类型	说明
start	Point3D	起点
end	Point3D	终点

CubicBezier模块的参数是四个点，建议先了解三次贝塞尔曲线的原理，然后就能明白这4个参数的意义。

参数名称	类型	说明
start_anchor	Point3D	起点
start_handle	Point3D	第一个控制点，影响曲线起点到中间部分的弯曲方向
end_handle	Point3D	第二个控制点，影响曲线中间部分到终点的弯曲方向
end_anchor	Point3D	终点

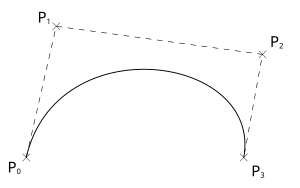
比如下面的贝塞尔曲线，其中:

• P_0 相当于参数start_anchor
• P_1 相当于参数start_handle
• P_2 相当于参数end_handle
• P_4 相当于参数end_anchor。

2. 使用示例

2.1. 带箭头的曲线

带箭头的曲线由起点 开始沿逆时针 方向旋转到终点。

CurvedArrow(
    LEFT / 2 + UP,
    RIGHT / 2 + UP,
    color=BLUE,
)
CurvedArrow(
    LEFT + UP / 2,
    RIGHT + UP / 2,
    color=RED,
)
CurvedDoubleArrow(
    LEFT * 2 + UP / 2,
    RIGHT * 2 + UP / 2,
    color=YELLOW,
)

CurvedDoubleArrow(
    RIGHT * 2 + DOWN * 1.6,
    LEFT * 2 + DOWN * 1.6,
    color=YELLOW,
)
CurvedArrow(
    RIGHT + DOWN * 1.6,
    LEFT + DOWN * 1.6,
    color=RED,
)
CurvedArrow(
    RIGHT / 2 + DOWN * 2.1,
    LEFT / 2 + DOWN * 2.1,
    color=BLUE,
)

2.2. 贝塞尔曲线绘制过程

贝塞尔曲线通过四个点就能绘制出非常平滑的曲线，其中的原理网络上有很多文章介绍，这里不再赘述。

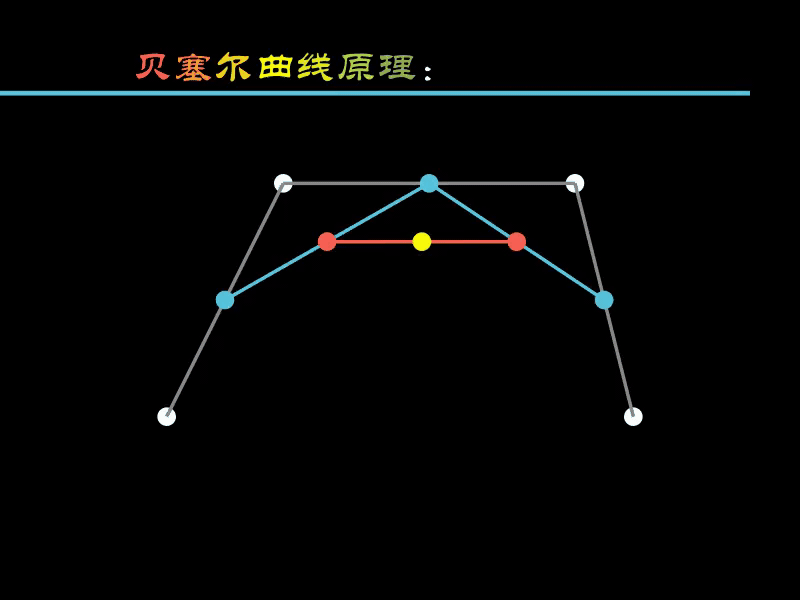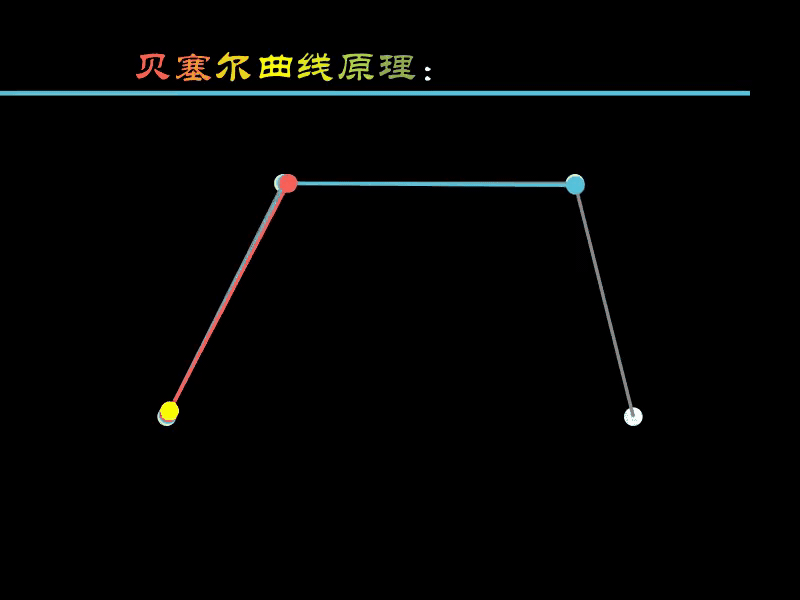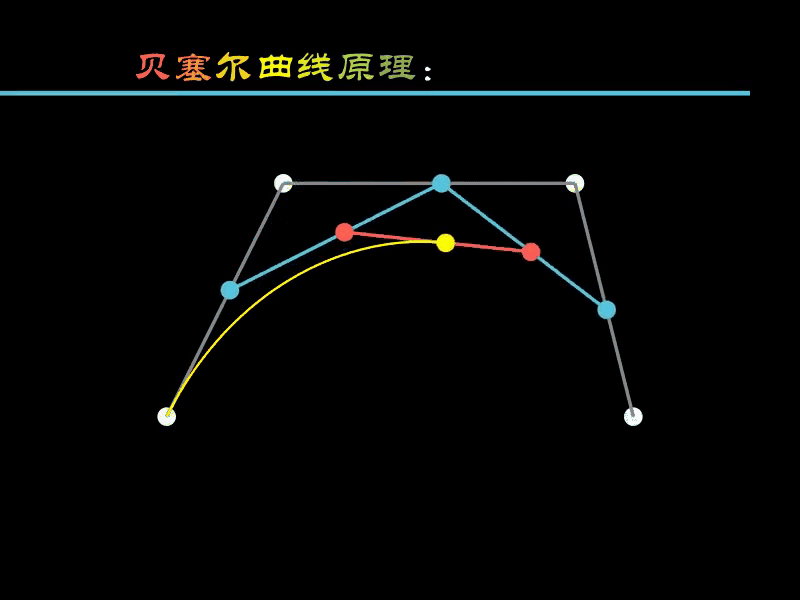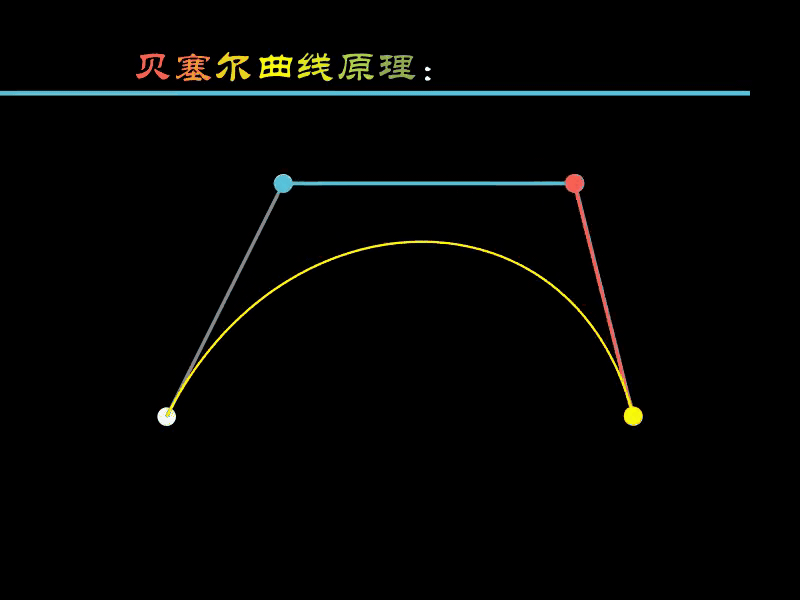
下面通过一个动画演示其绘制的原理。

1. 白色的点：用于绘制贝塞尔曲线的4个固定点
2. 蓝色点：根据4个白色点计算得出
3. 红色点：根据3个蓝色点计算得出
4. 黄色点：根据2个红色点计算得出

蓝色点 沿着白色点 连接的线移动，红色点 随蓝色点联动，黄色点随红色点联动，

黄色点的运动轨迹就是绘制出的曲线。

有了CubicBezier模块，可以根据四个点直接绘制贝塞尔曲线，效果和上面的一样，只是代码会简化很多。

points = [
    LEFT * 2 + DOWN,
    LEFT + UP,
    RIGHT * 1.5 + UP,
    RIGHT * 2 + DOWN,
]

CubicBezier(
    points[0],
    points[1],
    points[2],
    points[3],
    color=YELLOW,
)

2.3. 绘制爱心

贝塞尔曲线可以绘制非常光滑的曲线，理论上可以绘制各种复杂的曲线图形。

下面尝试用三次贝塞尔曲线来绘制一个爱心的图案。

points = [
    2 * DOWN * 0.5,
    2 * LEFT,
    2 * (LEFT + UP),
    2 * UP * 0.5,
]
# 左半部分
CubicBezier(
    points[0],
    points[1],
    points[2],
    points[3],
    color=RED,
)

points = [
    2 * DOWN * 0.5,
    2 * RIGHT * 1,
    2 * (RIGHT * 1 + UP),
    2 * UP * 0.5,
]
# 右半部分
CubicBezier(
    points[0],
    points[1],
    points[2],
    points[3],
    color=GREEN,
)

3. 附件

文中完整的代码放在网盘中了（bezier.py），

下载地址: 完整代码 (访问密码: 6872)