在数据可视化世界中,我们经常用直方图来描述数据的分布情况,但今天我想介绍两种特别而优雅的点状图变体:威尔金森点状图 和麦穗图。
它们像数据世界的"点彩派"画家,用简单的点创造出丰富的信息层次。
与直方图相比,这种点绘法不仅能够更直观地展示数据分布的细节,还能更好地揭示数据之间的关系和模式,使得观察者能够从更广阔的视角理解数据集的特点。
1. 威尔金森点状图
想象一下,你有一袋彩色弹珠,需要按颜色分类展示。如果只是简单地把所有弹珠倒出来,它们会杂乱无章。
但如果你为每种颜色准备一个小盒子,把相同颜色的弹珠整齐地堆叠在里面,这就是威尔金森点状图 的基本思想。
威尔金森点状图将数据点堆叠在对应的数值区域,形成类似直方图的分布展示,但保留了每个数据点的个体性。
它不是用条形的高度表示频率,而是用实际的数据点数量来可视化分布。
下面基于matplotlib库封装了一个绘制威尔金森点状图的函数。
python
def wilkinson_dot_plot(
data, bins=10, dot_size=40, dot_spacing=0.8, show_stats=True, random_seed=42
):
"""
创建威尔金森点状图
参数:
data: 输入数据(一维数组)
bins: 分组数量或分组边界
dot_size: 点的大小
dot_spacing: 点之间的垂直间距
random_seed: 随机种子
"""
np.random.seed(random_seed)
# 创建图形
fig, ax = plt.subplots(figsize=(10, 7))
# 计算直方图数据
hist, bin_edges = np.histogram(data, bins=bins)
# 为每个分组创建点
max_count = 0 # 记录最大堆叠高度
bin_centers = [] # 保存每个分组的中心位置
# 省略...
plt.tight_layout()
return fig, ax, (bin_edges, hist)威尔金森点状图的核心算法可以分解为几个步骤:
- 数据分箱:将连续数据分成若干个等宽的区间
- 点位置计算:在每个区间内,将数据点垂直堆叠
- 避免重叠:通过调整点的垂直位置防止重叠,同时保持可读性
使用起来也简单:
python
# 生成示例数据
np.random.seed(42)
# 数据集:正态分布
data_normal = np.random.normal(100, 15, 100)
dot_size = 200
# 创建威尔金森点状图
fig1, ax1, stats1 = wilkinson_dot_plot(data_normal, bins=12, dot_size=dot_size)
plt.show()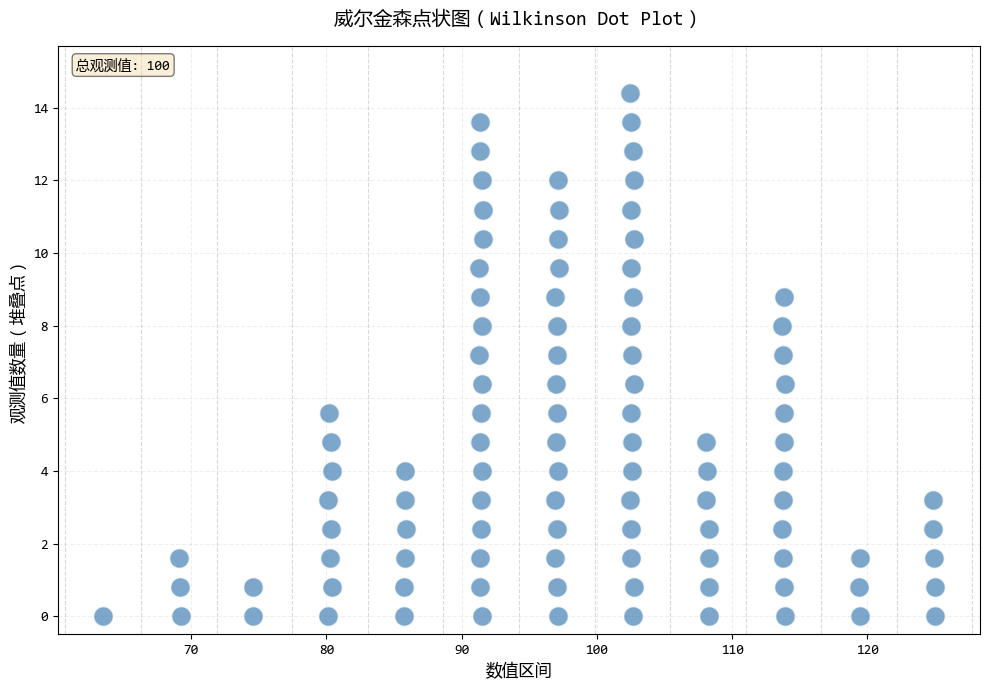
2. 麦穗图
如果把威尔金森点状图 比作整齐堆叠的弹珠,那么麦穗图就像是田野中的麦穗------每个数据点都像一颗麦粒,精确地生长在自己的位置上,展示其实际数值。
麦穗图 是威尔金森点状图的一种变体,它将点放置在其实际数值位置,而不是分组中心。
这保留了数据的精确性,同时通过堆叠避免了重叠。
麦穗图 的实现与威尔金森点状图 类似,但有一个关键区别:点沿x轴放置在实际数据值位置,而不是分组中心。
python
# 封装麦穗图函数
def strip_plot(
data,
bin_edges=None,
bins=10,
dot_size=40,
dot_spacing=0.8,
jitter_amount=0.2,
random_seed=42,
):
"""
创建麦穗图(在威尔金森点状图基础上显示实际值)
参数:
data: 输入数据(一维数组)
bin_edges: 可选,使用预定义的分组边界
bins: 如果未提供bin_edges,则使用此参数创建分组
dot_size: 点的大小
dot_spacing: 点之间的垂直间距
jitter_amount: 水平抖动程度(避免重叠)
random_seed: 随机种子
"""
np.random.seed(random_seed)
# 创建图形
fig, ax = plt.subplots(figsize=(10, 7))
# 如果没有提供分组边界,则计算
if bin_edges is None:
hist, bin_edges = np.histogram(data, bins=bins)
else:
hist, bin_edges = np.histogram(data, bins=bin_edges)
# 对数据进行排序
sorted_data = np.sort(data)
# 将数据分配到对应的分组
data_by_bin = []
for i in range(len(bin_edges) - 1):
lower, upper = bin_edges[i], bin_edges[i + 1]
bin_data = sorted_data[(sorted_data >= lower) & (sorted_data < upper)]
data_by_bin.append(bin_data)
# 处理最后一个分组(包含最大值)
if len(data) > 0:
last_bin_data = sorted_data[sorted_data >= bin_edges[-2]]
if len(data_by_bin) > 0:
data_by_bin[-1] = last_bin_data
# 绘制麦穗图
max_points_in_bin = 0
# 省略 ...
plt.tight_layout()
return fig, ax, (bin_edges, data_by_bin)使用起来也简单:
python
# 生成示例数据
np.random.seed(42)
# 数据集:正态分布
data_normal = np.random.normal(100, 15, 100)
dot_size = 200
# 创建的麦穗图
bin_edges = 12
fig2, ax2, stats2 = strip_plot(
data_normal, bin_edges=bin_edges, dot_size=dot_size, jitter_amount=0.15
)
plt.show()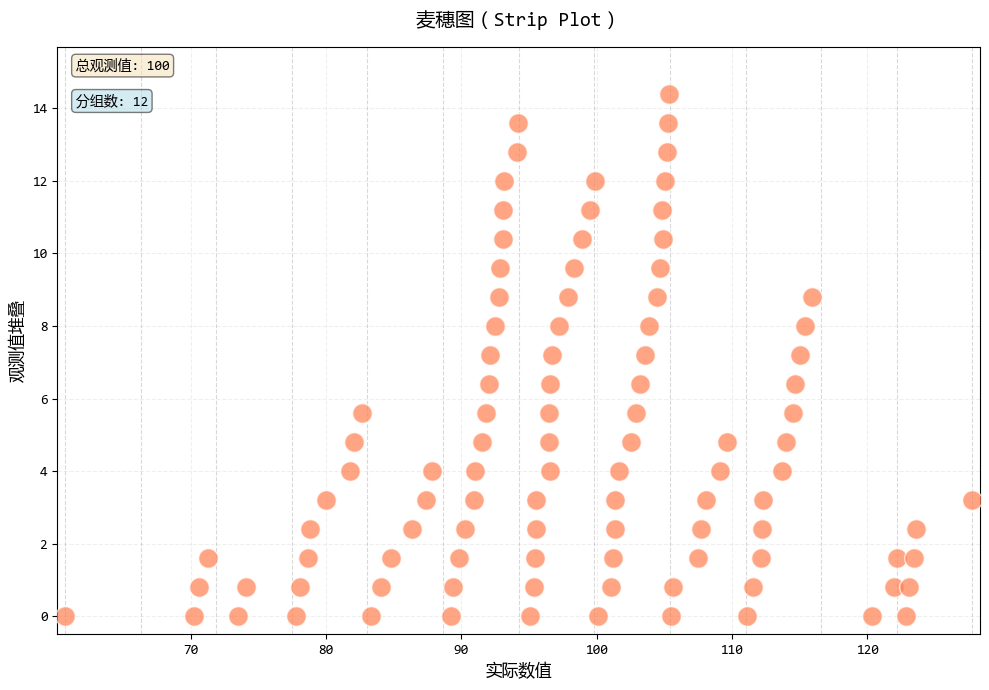
3. 两种图的应用场景
下面模拟一个学生考试成绩分布的分析场景,看看上面两种点状图的应用。
python
# 示例:学生考试成绩分布分析
print("示例:学生考试成绩分布分析")
print("-" * 40)
# 创建模拟的考试成绩数据
np.random.seed(42)
exam_scores = np.concatenate(
[
np.random.normal(65, 8, 45), # 中等水平学生
np.random.normal(85, 6, 30), # 优秀学生
np.random.normal(45, 10, 24), # 需要帮助的学生
]
)
# 过滤掉不合理分数
exam_scores = np.clip(exam_scores, 0, 100)
print(f"学生总数: {len(exam_scores)}")
print(f"分数范围: {exam_scores.min():.1f} - {exam_scores.max():.1f}")
print(f"平均分: {exam_scores.mean():.1f}")
print(f"及格率: {(exam_scores >= 60).sum() / len(exam_scores) * 100:.1f}%\n")
# 使用威尔金森点状图
print("创建威尔金森点状图...")
fig1, ax1, stats1 = wilkinson_dot_plot(
exam_scores,
bins=[0, 40, 60, 70, 80, 90, 100],
)
plt.show()
# 使用麦穗图
print("创建麦穗图...")
fig2, ax2, stats2 = strip_plot(
exam_scores,
bins=[0, 40, 60, 70, 80, 90, 100],
jitter_amount=0.15,
)
plt.show()
## 输出结果:
'''
示例:学生考试成绩分布分析
----------------------------------------
学生总数: 99
分数范围: 25.1 - 94.4
平均分: 65.3
及格率: 63.6%
'''
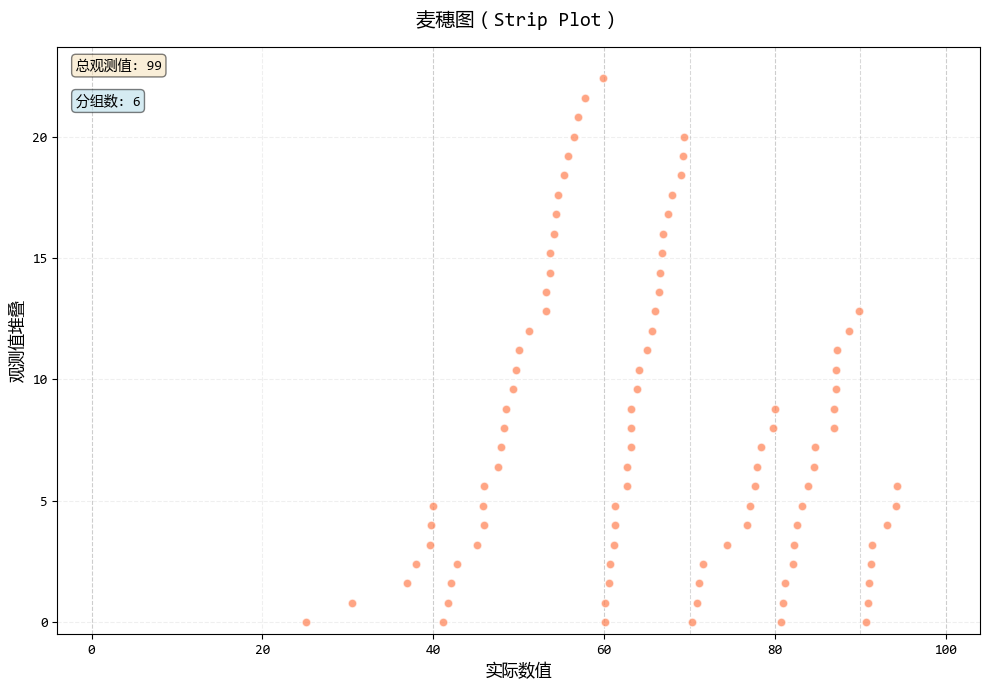
在学生考试成绩分析这个场景中:
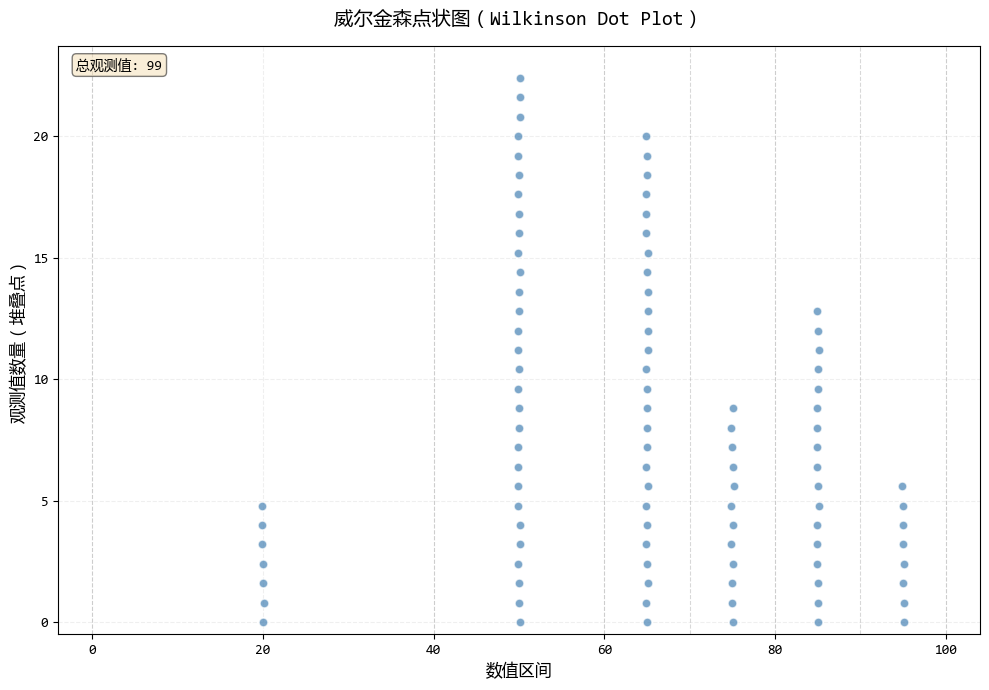
- 威尔金森点状图:将分数分组成区间(如60-70分),所有该区间的学生点都堆叠在区间中心,清晰地展示了分数段的整体分布形态,类似直方图但能看到个体点。
- 麦穗图:点在实际分数位置堆叠(如65分、68分等),既显示了每个学生的具体分数,又通过垂直堆叠避免了重叠,保留了数据的精确性。
总的来说,威尔金森点状图 看分布形态(区间视角 ),麦穗图 看具体数值(精确视角)。
4. 总结
威尔金森点状图 和麦穗图为数据可视化工具箱增添了优雅而实用的工具。
它们填补了传统直方图 和散点图之间的空白,提供了同时展示数据分布和个体数据点的独特方式。
在数据可视化中,选择合适的图表类型就像选择正确的工具来完成工作。
威尔金森点状图 和麦穗图提供了独特的视角,让我们能够同时看到森林和树木------既理解整体分布,又关注个体数据点。
完整代码分享:威尔金森与麦穗图.ipynb (访问密码: 6872)