目录
- 一、预训练
- 二、语言模型
- 三、词向量
- 四、Word2Vec 模型
- 五、自然语言处理的预训练模型
- 六、RNN 和 LSTM
- 七、ELMo 模型
- 八、Attention
- 九、Position Embedding
- 十、Transformer
- 十一、Transformer 动态流程展示
- 十二、GPT 模型
- 十三、BERT 模型
- 十四、BERT 下游任务改造
- 十五、预训练语言模型总结
- 十六、参考资料
Bert 最近很火,应该是最近最火爆的 AI 进展,网上的评价很高,从模型创新角度看一般,创新不算大。但是架不住效果太好了,基本刷新了很多 NLP 的任务的最好性能,有些任务还被刷爆了,这个才是关键。另外一点是 Bert 具备广泛的通用性,就是说绝大部分 NLP 任务都可以采用类似的两阶段模式直接去提升效果,这个第二关键。客观的说,把 Bert 当做最近两年 NLP 重大进展的集大成者更符合事实。
本文的主题是预训练语言模型的前世今生,会大致说下 NLP 中的预训练技术是一步一步如何发展到 Bert 模型的,从中可以很自然地看到 Bert 的思路是如何逐渐形成的,Bert 的历史沿革是什么,继承了什么,创新了什么,为什么效果那么好,主要原因是什么,以及为何说模型创新不算太大,为何说 Bert 是近年来 NLP 重大进展的集大成者。
预训练语言模型的发展并不是一蹴而就的,而是伴随着诸如词嵌入、序列到序列模型及 Attention 的发展而产生的。
DeepMind 的计算机科学家 Sebastian Ruder 给出了 21 世纪以来,从神经网络技术的角度分析,自然语言处理的里程碑式进展,如下表所示:
| 年份 | 2013 年 | 2014 年 | 2015 年 | 2016 年 | 2017 年 |
|---|---|---|---|---|---|
| 技术 | word2vec | GloVe | LSTM/Attention | Self-Attention | Transformer |
| 年份 | 2018 年 | 2019 年 | 2020 年 |
|---|---|---|---|
| 技术 | GPT/ELMo/BERT/GNN | XLNet/BoBERTa/GPT-2/ERNIE/T5 | GPT-3/ELECTRA/ALBERT |
本篇文章将会通过上表显示的 NLP 中技术的发展史一一叙述,由于 19 年后的技术大都是 BERT 的变体,在这里不会多加叙述,读者可以自行加以了解。
一、预训练
1.1 图像领域的预训练
在介绍图像领域的预训练之前,我们首先介绍下卷积神经网络(CNN),CNN 一般用于图片分类任务,并且CNN 由多个层级结构组成,不同层学到的图像特征也不同,越浅的层学到的特征越通用(横竖撇捺),越深的层学到的特征和具体任务的关联性越强(人脸-人脸轮廓、汽车-汽车轮廓),如下图所示:

由此,当领导给我们一个任务:阿猫、阿狗、阿虎的图片各十张,然后让我们设计一个深度神经网络,通过该网络把它们三者的图片进行分类。
对于上述任务,如果我们亲手设计一个深度神经网络基本是不可能的,因为深度学习一个弱项就是在训练阶段对于数据量的需求特别大,而领导只给我们合计三十张图片,显然这是不够的。
虽然领导给我们的数据量很少,但是我们是否可以利用网上现有的大量已做好分类标注的图片。比如 ImageNet 中有 1400 万张图片,并且这些图片都已经做好了分类标注。
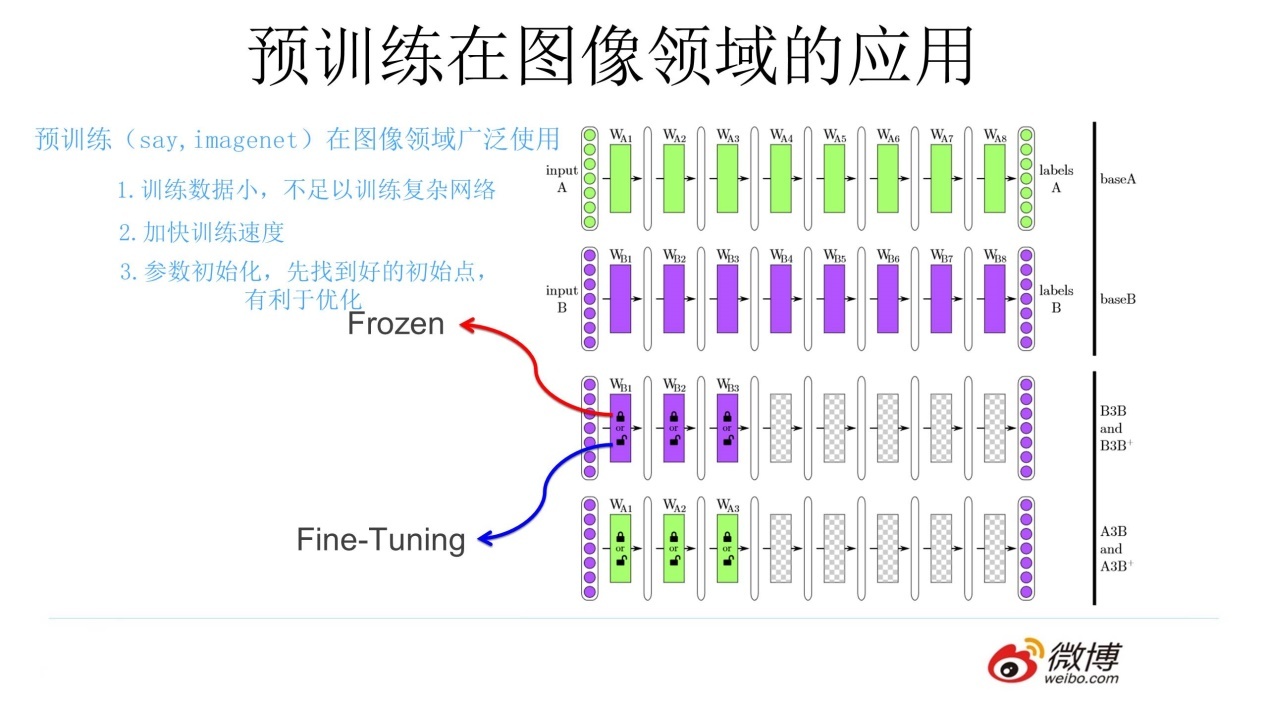
上述利用网络上现有图片的思想就是预训练的思想,具体做法就是:
- 通过 ImageNet 数据集我们训练出一个模型 A
- 由于上面提到 CNN 的浅层学到的特征通用性特别强,我们可以对模型 A 做出一部分改进得到模型 B(两种方法):
- 冻结:浅层参数使用模型 A 的参数,高层参数随机初始化,浅层参数一直不变,然后利用领导给出的 30 张图片训练参数
- 微调:浅层参数使用模型 A 的参数,高层参数随机初始化,然后利用领导给出的 30 张图片训练参数,但是在这里浅层参数会随着任务的训练不断发生变化
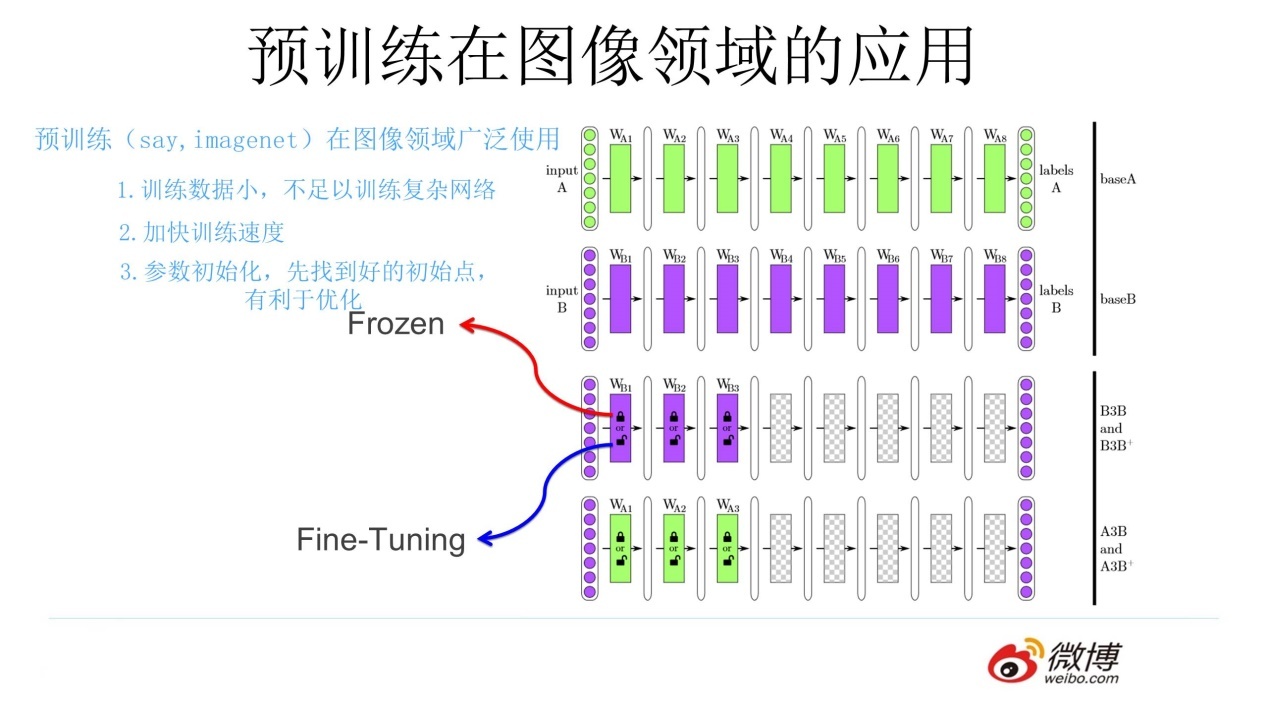
通过上述的讲解,对图像预训练做个总结(可参照上图):对于一个具有少量数据的任务 A,首先通过一个现有的大量数据搭建一个 CNN 模型 A,由于 CNN的浅层学到的特征通用性特别强,因此在搭建一个 CNN 模型 B,其中模型 B 的浅层参数使用模型 A 的浅层参数,模型 B 的高层参数随机初始化,然后通过冻结或微调的方式利用任务 A 的数据训练模型 B,模型 B 就是对应任务 A 的模型。
1.2 预训练的思想
有了图像领域预训练的引入,我们在此给出预训练的思想:任务 A 对应的模型 A 的参数不再是随机初始化的,而是通过任务 B 进行预先训练得到模型 B,然后利用模型 B 的参数对模型 A 进行初始化,再通过任务 A 的数据对模型 A 进行训练。注:模型 B 的参数是随机初始化的。
二、语言模型
想了解预训练语言模型,首先得了解什么是语言模型。
语言模型通俗点讲就是**计算一个句子的概率。**也就是说,对于语言序列 w1,w2,⋯,wn�1,�2,⋯,��,语言模型就是计算该序列的概率,即 P(w1,w2,⋯,wn)�(�1,�2,⋯,��)。
下面通过两个实例具体了解上述所描述的意思:
- 假设给定两句话 "判断这个词的磁性" 和 "判断这个词的词性",语言模型会认为后者更自然。转化成数学语言也就是:P(判断,这个,词,的,词性)>P(判断,这个,词,的,磁性)�(判断,这个,词,的,词性)>�(判断,这个,词,的,磁性)
- 假设给定一句话做填空 "判断这个词的____",则问题就变成了给定前面的词,找出后面的一个词是什么,转化成数学语言就是:P(词性|判断,这个,词,的)>P(磁性|判断,这个,词,的)�(词性|判断,这个,词,的)>�(磁性|判断,这个,词,的)
通过上述两个实例,可以给出语言模型更加具体的描述:给定一句由 n� 个词组成的句子 W=w1,w2,⋯,wn�=�1,�2,⋯,��,计算这个句子的概率 P(w1,w2,⋯,wn)�(�1,�2,⋯,��),或者计算根据上文计算下一个词的概率 P(wn|w1,w2,⋯,wn−1)�(��|�1,�2,⋯,��−1)。
下面将介绍语言模型的两个分支,统计语言模型和神经网络语言模型。
2.1 统计语言模型
统计语言模型的基本思想就是计算条件概率。
给定一句由 n� 个词组成的句子 W=w1,w2,⋯,wn�=�1,�2,⋯,��,计算这个句子的概率 P(w1,w2,⋯,wn)�(�1,�2,⋯,��) 的公式如下(条件概率乘法公式的推广,链式法则):
P(w1,w2,⋯,wn)=P(w1)P(w2|w1)P(w3|w1,w2)⋯p(wn|w1,w2,⋯,wn−1)=∏iP(wi|w1,w2,⋯,wi−1)�(�1,�2,⋯,��)=�(�1)�(�2|�1)�(�3|�1,�2)⋯�(��|�1,�2,⋯,��−1)=∏��(��|�1,�2,⋯,��−1)
对于上一节提到的 "判断这个词的词性" 这句话,利用上述的公式,可以得到:
P(判断,这个,词,的,词性)=P(判断)P(这个|判断)P(词|判断,这个)P(的|判断,这个,词)P(词性|判断,这个,词,的)P(判断,这个,词,的,词性)�(判断,这个,词,的,词性)=�(判断)�(这个|判断)�(词|判断,这个)�(的|判断,这个,词)�(词性|判断,这个,词,的)�(判断,这个,词,的,词性)
对于上一节提到的另外一个问题,当给定前面词的序列 "判断,这个,词,的" 时,想要知道下一个词是什么,可以直接计算如下概率:
P(wnext|判断,这个,词,的)公式(1)�(�����|判断,这个,词,的)公式(1)
其中,wnext∈V�����∈� 表示词序列的下一个词,V� 是一个具有 |V||�| 个词的词典(词集合)。
对于公式(1),可以展开成如下形式:
P(wnext|判断,这个,词,的)=count(wnext,判断,这个,词,的)count(判断,这个,词,的)公式(2)�(�����|判断,这个,词,的)=�����(�����,判断,这个,词,的)�����(判断,这个,词,的)公式(2)
对于公式(2),可以把字典 V� 中的多有单词,逐一作为 wnext�����,带入计算,最后取最大概率的词作为 wnext����� 的候选词。
如果 |V||�| 特别大,公式(2)的计算将会非常困难,但是我们可以引入马尔科夫链的概念(当然,在这里只是简单讲讲如何做,关于马尔科夫链的数学理论知识可以自行查看其他参考资料)。
假设字典 V� 中有 "火星" 一词,可以明显发现 "火星" 不可能出现在 "判断这个词的" 后面,因此(火星,判断,这个,词,的)这个组合是不存在的,并且词典中会存在很多类似于 "火星" 这样的词。
进一步,可以发现我们把(火星,判断,这个,词,的)这个组合判断为不存在,是因为 "火星" 不可能出现在 "词的" 后面,也就是说我们可以考虑是否把公式(1)转化为
P(wnext|判断,这个,词,的)≈P(wnext|词,的)公式(3)�(�����|判断,这个,词,的)≈�(�����|词,的)公式(3)
公式(3)就是马尔科夫链的思想:假设 wnext����� 只和它之前的 k� 个词有相关性,k=1�=1 时称作一个单元语言模型,k=2�=2 时称为二元语言模型。
可以发现通过马尔科夫链后改写的公式计算起来将会简单很多,下面我们举个简单的例子介绍下如何计算一个二元语言模型的概率。
其中二元语言模型的公式为:
P(wi|wi−1)=count(wi−1,wi)count(wi−1)公式(4)�(��|��−1)=�����(��−1,��)�����(��−1)公式(4)
假设有一个文本集合:
basic
“词性是动词”
“判断单词的词性”
“磁性很强的磁铁”
“北京的词性是名词”对于上述文本,如果要计算 P(词性|的)�(词性|的) 的概率,通过公式(4),需要统计 "的,词性" 同时按序出现的次数,再除以 "的" 出现的次数:
P(词性|的)=count(的,词性)count(的)=23公式(5)�(词性|的)=�����(的,词性)�����(的)=23公式(5)
上述文本集合是我们自定制的,然而对于绝大多数具有现实意义的文本,会出现数据稀疏的情况,例如训练时未出现,测试时出现了的未登录单词。
由于数据稀疏问题,则会出现概率值为 0 的情况(填空题将无法从词典中选择一个词填入),为了避免 0 值的出现,会使用一种平滑的策略------分子和分母都加入一个非 0 正数,例如可以把公式(4)改为:
P(wi|wi−1)=count(wi−1,wi)+1count(wi−1)+|V|公式(6)
excel计算时间差-显示每堂课时间-CSDN博客 https://blog.csdn.net/qq_41517071/article/details/141255523?spm=1000.2115.3001.6382&utm_medium=distribute.pc_feed_v2.none-task-blog-personrec_tag-4-141255523-null-null.329^v9^%E4%B8%AA%E6%8E%A8pc%E9%A6%96%E9%A1%B5%E6%8E%A8%E8%8D%90%E2%80%94%E6%A1%B67&depth_1-utm_source=distribute.pc_feed_v2.none-task-blog-personrec_tag-4-141255523-null-null.329^v9^%E4%B8%AA%E6%8E%A8pc%E9%A6%96%E9%A1%B5%E6%8E%A8%E8%8D%90%E2%80%94%E6%A1%B67