点击蓝字

关注我们
AI TIME欢迎每一位AI爱好者的加入!
点击 阅读原文 观看作者直播讲解回放!
作者简介
孙浩鑫,复旦大学博士生,主要研究方向为大规模图上快速算法设计。
概述
森林矩阵在网络科学、观点动力学和机器学习相关应用中扮演着至关重要的角色,深刻刻画了网络的结构信息与内在联系。在本文中,我们研究了在演化中的图(与静态图相比,更准确地代表了现实世界网络的动态特性)中查询森林矩阵元素的问题。为了应对演化图所带来的独特挑战,我们首先为静态图中森林矩阵元素查询提出了两种近似算法,SFQ和SFQPlus。SFQ采用了森林矩阵的概率解释,而SFQPlus则结合了一种新颖的方差减少技术,我们理论证明了SFQPlus拥有更小的方差,因而可以提供更高的精确度。基于这两种算法,我们进一步设计了两种动态算法,这些算法的核心是高效地维护一系列带根的生成森林列表。这种方法确保了更新(包括边的添加和删除)以及查询矩阵元素的运行时间复杂度为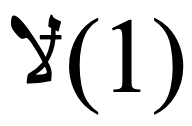 ,并且提供了森林矩阵元素的无偏估计。最后,通过在各种真实世界网络上进行广泛的实验,我们证明了我们算法的效率和有效性。特别是,我们的算法可以扩展到拥有超过四千万个节点的大规模网络中。
,并且提供了森林矩阵元素的无偏估计。最后,通过在各种真实世界网络上进行广泛的实验,我们证明了我们算法的效率和有效性。特别是,我们的算法可以扩展到拥有超过四千万个节点的大规模网络中。
论文地址:https://dl.acm.org/doi/10.1145/3637528.3671822
AITIME
01
Background
本文首先定义了森林矩阵Ω,它是单位矩阵I与拉普拉斯矩阵L和的逆矩阵。拉普拉斯矩阵L由图的度矩阵D减去邻接矩阵A得到。森林矩阵在有向图中的元素值介于0到1之间,且每行元素之和为1,表现为行随机矩阵。其对角元素在网络分析中作为森林中心性指标具有特别意义,已经有研究深入探讨了森林中心性的性质与应用。其非对角元素则可用来衡量两点之间"距离"的远近,也有重要意义。

除此之外,在采用数学建模刻画社会观点的传播与扩散时,森林矩阵在Friedkin-Johnsen(FJ)模型中被视为核心矩阵。该模型是观点动力学领域的著名模型,曾被用来解释巴黎协定达成共识的过程。然而,鉴于社交网络等现实世界的网络不断变化,本文关注于在不断演化的图上面提出快速查询森林矩阵元素的方法,以适应网络的动态特性。
AITIME
02
Contributions
该研究的贡献主要体现在两个方面:首先,在静态图领域,研究者提出了森林矩阵元素的概率解释,并开发了两种快速算法SFQ和SFQ+,其中SFQ+算法通过引入创新的方差减少技术,实现了性能上的显著提升。其次,针对演化图,研究者专注于边的插入和删除操作,因为节点的插入和删除可以看成一系列连续的边的增删操作。为此,作者设计了一种策略,利用特定的内存数据结构存储图信息,并在图更新时快速调整该结构,以实现在O(1)时间内快速更新和查询所需元素。

AITIME
03
Spanning Converging Forest
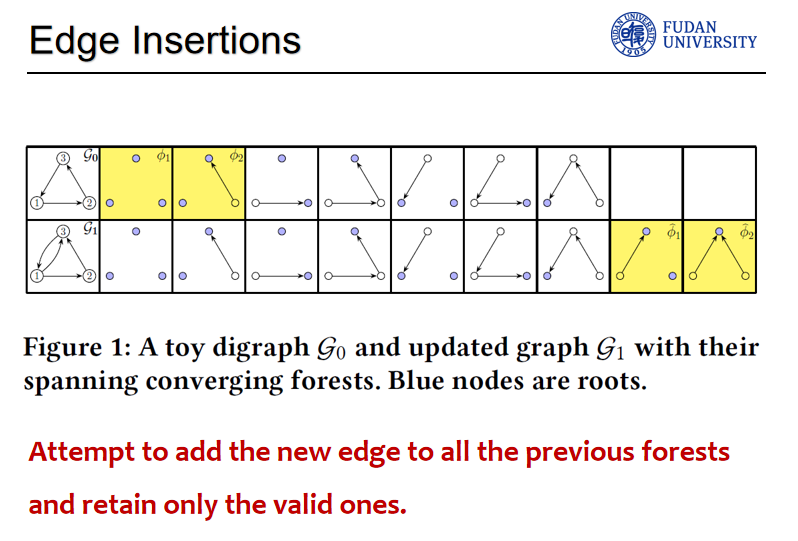
作者首先介绍了带根生成森林的概念,并解释了为何称之为森林矩阵,原因在于该矩阵的元素与图上的带根生成森林紧密相关。
随后,研究者阐释了带根生成树的定义:它是一个连通图且形态为树,具有一个特定的根节点,该节点的出度为0,而树中其他所有节点的出度均为1。带根生成森林由多个这样的连通分支组成,每个分支都是一棵以特定节点为根的树。
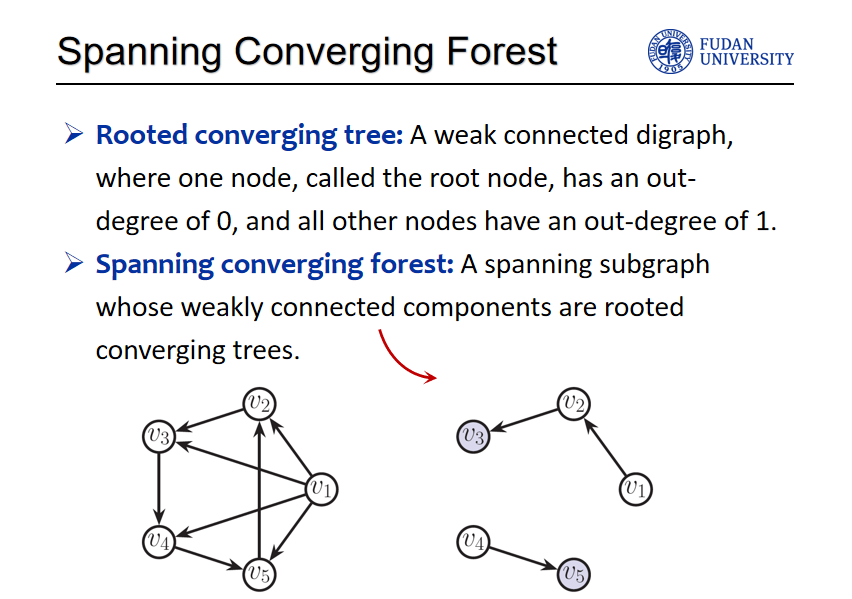
例如,通过观察提供的图示,可以看到左侧的图是一个包含五个顶点和多条边的小型图。而右侧的图则展示了该图中的一棵生成森林,其中三节点和五节点被选为根节点,而图中的其他节点则是森林中的普通成员。
AITIME
04
Sampling Algorithm SFQ
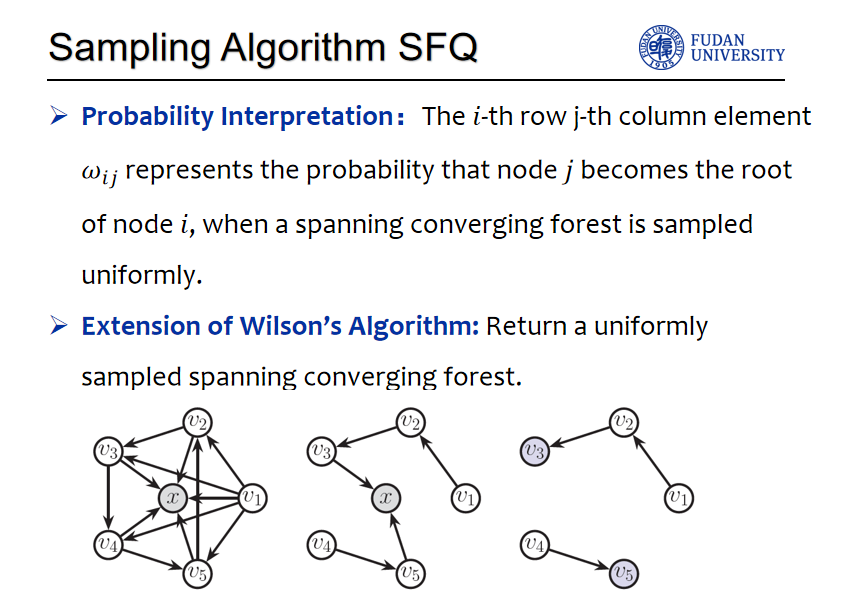
作者通过矩阵森林定理阐释了森林矩阵元素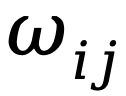 的含义,它代表在均匀生成的带根生成森林中,节点i的根为节点j的概率。为了生成这样的均匀带根生成森林,研究者采用了Wilson算法的扩展版本,Wilson提出的原始的算法可以返回一个给定根节点的生成树,这里作者使用了它的拓展版本,用于生成带根生成森林。左侧的图示展示了这一过程的起始步骤。
的含义,它代表在均匀生成的带根生成森林中,节点i的根为节点j的概率。为了生成这样的均匀带根生成森林,研究者采用了Wilson算法的扩展版本,Wilson提出的原始的算法可以返回一个给定根节点的生成树,这里作者使用了它的拓展版本,用于生成带根生成森林。左侧的图示展示了这一过程的起始步骤。
AITIME
05
Static Graphs-- SFQ
在前面的图中,作者通过新增一个第6个顶点x,并在原图中加入五条指向新节点x的新边,这样生成了拓展图。接着,使用Wilson算法生成了一个以x为根的生成树。第三步,删除了新顶点x及其指向它的边,从而获得了一个均匀的带根生成森林。这种方法具有O(n)的时间复杂度,适用于大规模网络,并且支持并行处理,能够在多个核上同时运行,显著提高了效率。

作者提出了一种基础算法,称为SFQ算法。该算法在查询时,基于已采样的l个森林,计算节点的根为节点的概率。SFQ算法的时间复杂度为O(l),这表明它在处理查询时效率较高。
AITIME
06
Static Graphs-- SFQPLUS



AITIME
07
Algorithms SFQ and SFQPLUS
作者在静态图上提出了两种算法:SFQ和SFQ Plus。SFQ算法首先利用了威尔逊算法的扩展和矩阵森林定理,并且提供了一个无偏估计。而SFQ Plus算法由于聚合了更多的信息,不仅保持了无偏估计的特性,还拥有比SFQ更小的方差,从而提供了更优的结果。简而言之,研究者提出的第二个算法,SFQ Plus,在性能上超越了最初的SFQ算法。

AITIME
08
Evolving Graphs

AITIME
09
Edge Insertions






AITIME
10
Edge Deletions


具体而言,对应下列算法的中的第二行-第九行。

AITIME
11
Pruning Technique


AITIME
12
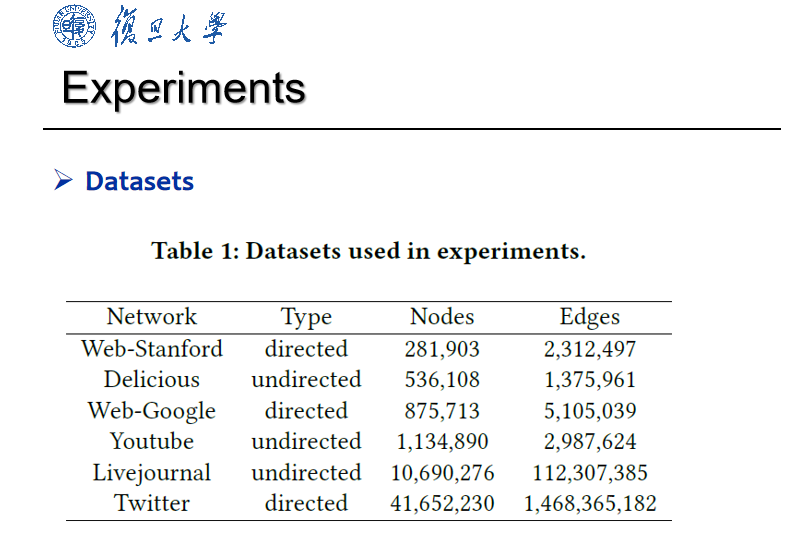
Experiments
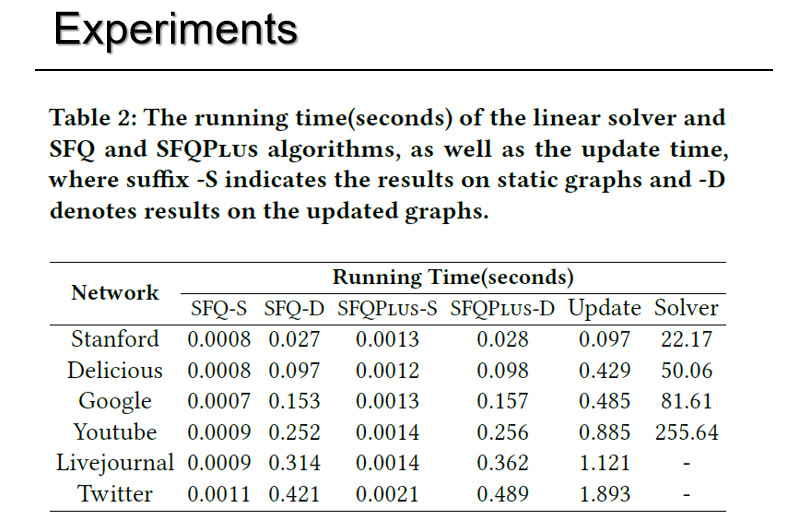
本文的算法通过一系列实验验证了其性能,结果表明,该算法能够高效地处理大规模网络,例如在推特网络上,算法能够顺利处理达到四千万节点的图,且运行过程中没有出现问题。这展示了算法在处理大规模数据集时的稳定性和可靠性。
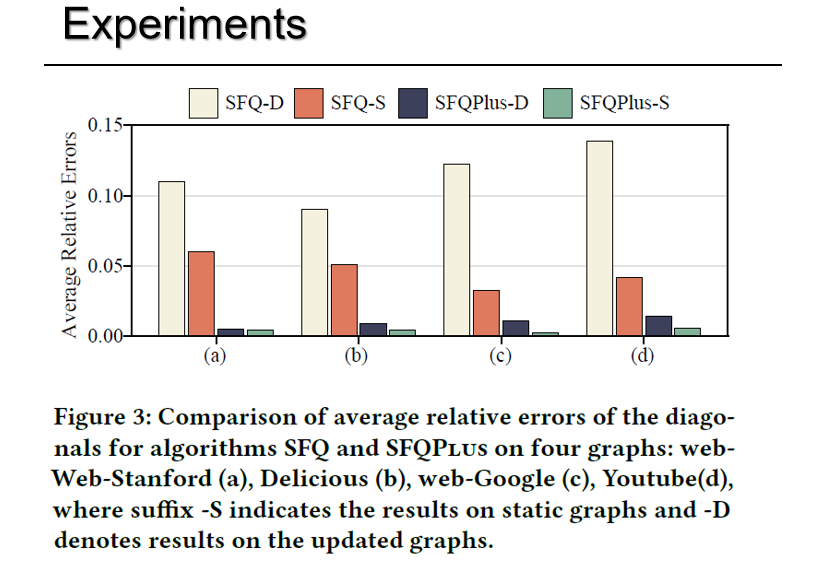
森林矩阵的对角元有重要意义,可用于衡量节点的中心性。作者首先对算法的对角元精度进行了测试,发现以平均相对误差为衡量标准,相较于SFQ算法,提出的SFQPlus算法精度有显著提高。作者在演化图与静态图上都进行了实验,发现算法在演化图上的误差高于静态图,这可能是由于生成森林数量增加导致相关性增强,使得误差随迭代次数增长。这一现象指明了未来研究需要关注的优化方向。
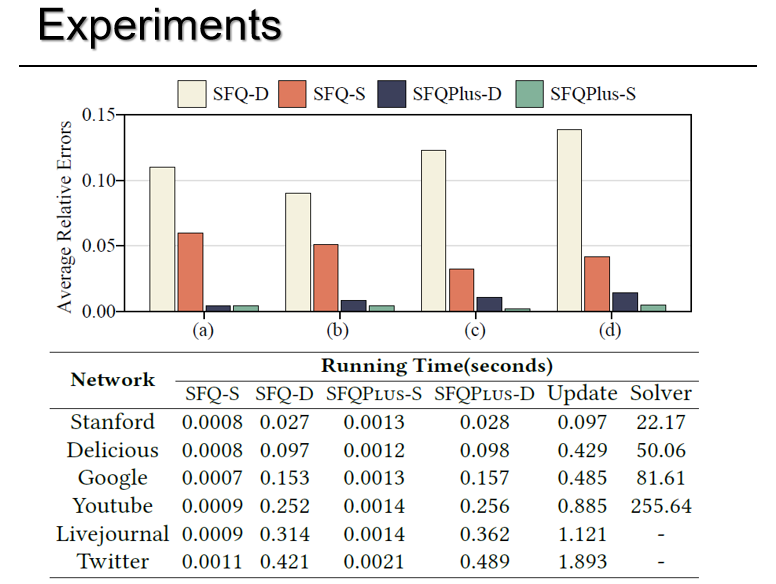

同时,常数时间的复杂度使得算法在查询和更新速度上表现出色,无论是在中小规模网络还是在拥有千万节点的大规模网络。如下表格展示了,当网络节点规模达到千万级别,当前最优秀的图求解器算法也无法在短时间内返回查询结果,而本文提出的算法则可以在极短时间内返回结果。
本篇文章由陈研整理

点击 阅读原文 观看作者直播讲解回放!
往期精彩文章推荐
论文解读 | ACL2024 Outstanding Paper:因果指导的主动学习方法:助力大语言模型自动识别并去除偏见
关于AI TIME
AI TIME源起于2019年,旨在发扬科学思辨精神,邀请各界人士对人工智能理论、算法和场景应用的本质问题进行探索,加强思想碰撞,链接全球AI学者、行业专家和爱好者,希望以辩论的形式,探讨人工智能和人类未来之间的矛盾,探索人工智能领域的未来。
迄今为止,AI TIME已经邀请了1800多位海内外讲者,举办了逾600场活动,超700万人次观看。

我知道你
在看
提出观点,表达想法,欢迎
留言

点击 阅读原文 观看作者直播讲解回放!