大家好,欢迎来到无限大的频道。
今日继续给大家带来力扣题解。
题目描述(简单):
公交站间的距离
环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
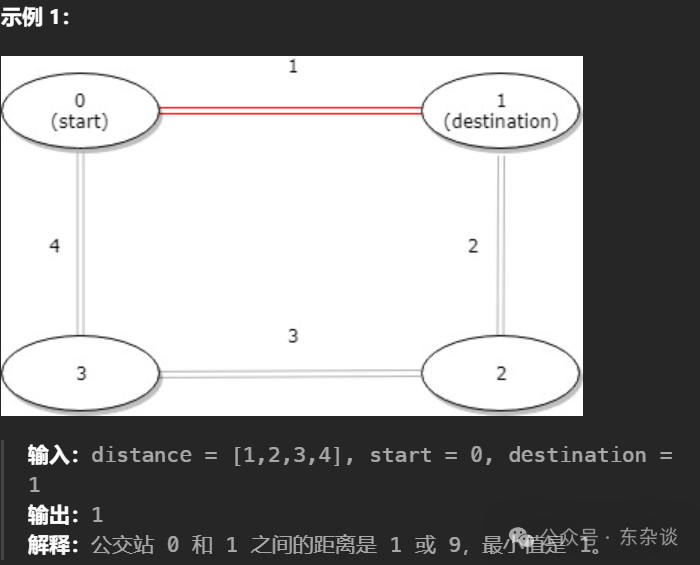
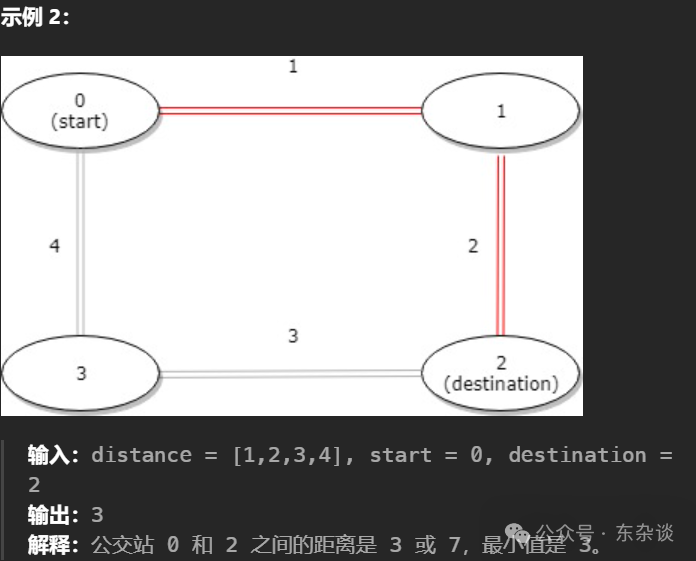
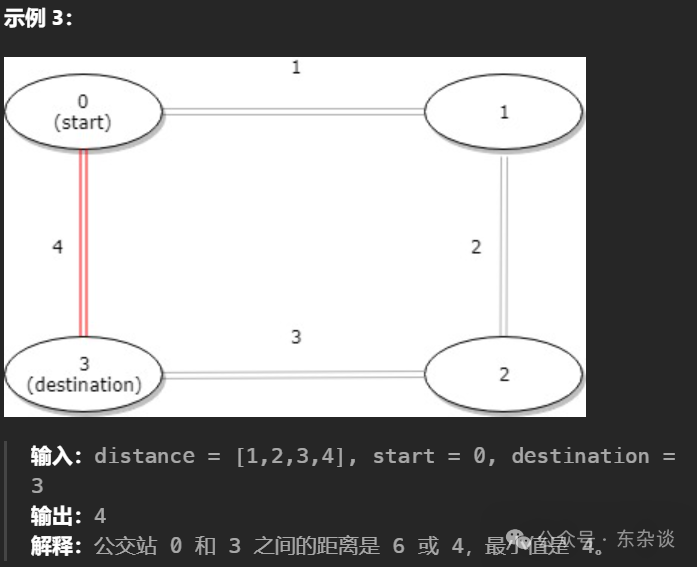
解题思路:
-
输入和初始化:
- 输入为公交站数 n、车站间距数组 distance、出发点 start 和目的地 destination。
-
计算顺时针距离:
- 从 start 到 destination 的顺时针距离可以通过计算 distance 数组中相应站点之间的距离累加得出。
-
计算逆时针距离:
- 逆时针距离可以通过计算从 destination 到 start 的总距离减去顺时针距离得出。这是因为在环形路线中,总距离是固定的。
-
取最小值:
-
最后,返回顺时针和逆时针距离中的最小值。
-
参考代码:
int distanceBetweenBusStops(int* distance, int distanceSize, int start, int destination) {
// 确保 start 是较小的索引
if (start > destination) {
int temp = start;
start = destination;
destination = temp;
}
// 计算顺时针距离
int clockwiseDistance = 0;
for (int i = start; i < destination; i++) {
clockwiseDistance += distance[i];
}
// 计算逆时针距离
int totalDistance = 0;
for (int i = 0; i < distanceSize; i++) {
totalDistance += distance[i];
}
int counterClockwiseDistance = totalDistance - clockwiseDistance;
// 返回最小距离
return clockwiseDistance < counterClockwiseDistance ? clockwiseDistance : counterClockwiseDistance;
}时间复杂度:
- 确保 `start` 是较小的索引:
if (start > destination) {
int temp = start;
start = destination;
destination = temp;
}
这部分代码只进行了一次比较和可能的交换,因此它的时间复杂度是 O(1)。
- 计算顺时针距离:
int clockwiseDistance = 0;
for (int i = start; i < destination; i++) {
clockwiseDistance += distance[i];
}
这个循环从 `start` 到 `destination` 之间的索引进行累加。假设 `start` 和 `destination` 之间的距离为 d,这个部分的时间复杂度是 O(d)。
- 计算总距离:
int totalDistance = 0;
for (int i = 0; i < distanceSize; i++) {
totalDistance += distance[i];
}
这个循环遍历整个 `distance` 数组,计算总距离。由于 `distanceSize` 为 n,这个部分的时间复杂度是 O(n)。
- 计算逆时针距离:
int counterClockwiseDistance = totalDistance - clockwiseDistance;
这部分只进行了一次减法运算,因此它的时间复杂度是 O(1)。
- 返回最小距离:
return clockwiseDistance < counterClockwiseDistance ? clockwiseDistance : counterClockwiseDistance;
这部分也是一个简单的比较和返回,所以时间复杂度也是 \(O(1)\)。
将所有部分的时间复杂度相加,我们得到:
-
计算顺时针距离:O(d)
-
计算总距离:O(n)
因此,整体的时间复杂度主要由这两个部分决定。由于 d可能最多等于 n(在最坏情况下,即 `start` 为 0,`destination` 为 n-1),所以我们可以将 d的复杂度视为 O(n)。
最终,这段代码的总时间复杂度是:
O(n)
空间复杂度:
在空间复杂度方面,代码中只使用了常量级别的额外空间(几个整型变量),因此空间复杂度是 O(1)。