一、最小二乘法（Least Squares Method）一般步骤
非线性最小二乘法是一种用于优化非线性系统模型的数学方法，它通过迭代过程来逐步逼近最优解。这种方法在处理非线性系统时非常有用，因为它允许模型在数据拟合过程中具有更灵活的形式。以下是使用非线性最小二乘法优化非线性系统模型的非线性最小二乘法：
-
模型建立：首先，你需要建立一个非线性模型，该模型能够描述系统的行为。这个模型通常形式为 f(x,θ)f(x,θ)，其中 xx 是输入变量，θθ 是模型参数。
-
定义残差函数：残差函数 r(θ)r(θ) 表示模型预测值与实际观测值之间的差异。在最小二乘法中，目标是最小化这个残差的平方和。
-
选择初始参数：为模型参数 θθ 选择一个初始值。这个初始值可以基于经验、先前的研究或其他估计方法得到。
-
迭代优化：使用如高斯-牛顿法、牛顿法或梯度下降法等迭代算法来更新参数 θθ。这些方法通过计算残差函数的梯度和/或海塞矩阵（Hessian）来寻找误差平方和的最小值。
-
收敛判断：在每次迭代后，检查参数更新是否足够小，或者残差是否已经足够接近零。如果满足收敛条件，则停止迭代；否则，继续迭代。
-
模型验证：一旦找到最优参数，使用这些参数在模型中进行预测，并与实际数据进行比较，以验证模型的准确性。
二、LSM原理及应用
最小二乘法原理：未知量的最可能值是使各项实际观测值和计算值之间差的平方乘以其精确度的数值以后的和最小。
也就是说：
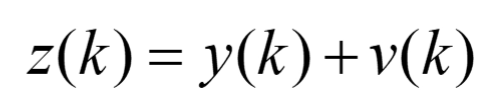
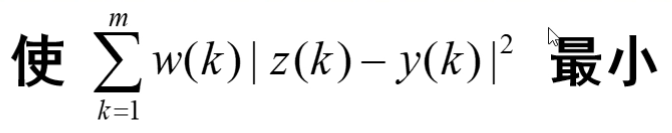
下面举一个例子说明算法原理：
通过试验确定热敏电阻阻值和温度之间的关系：
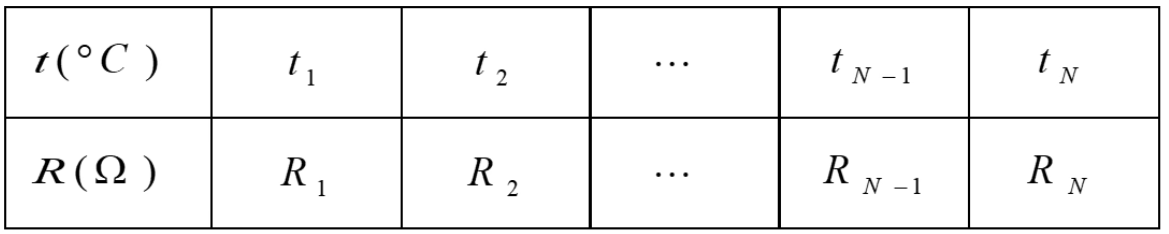
其中R = a + bt。
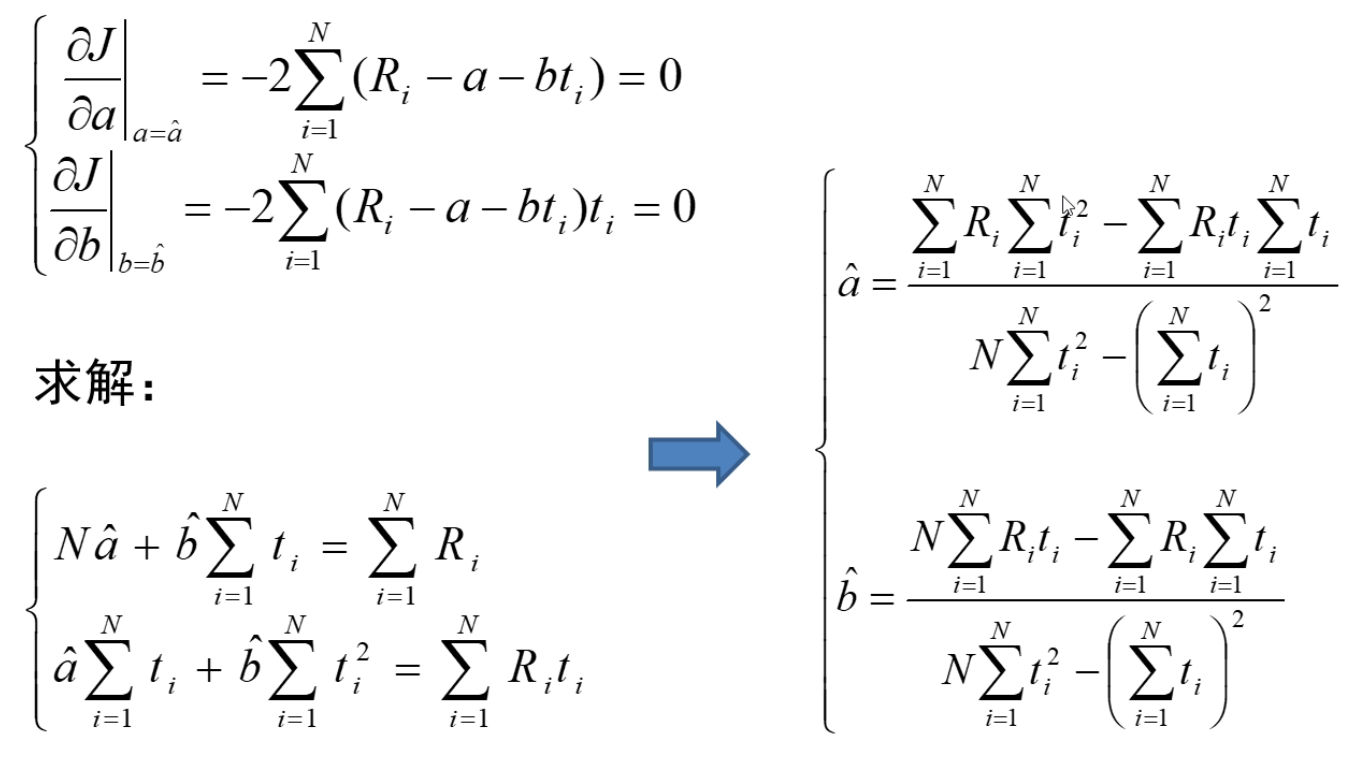
对于上面的例子，在matlab中实现并进行计算：
clear;
t = [20.5 26 32.7 40 51 61 73 80 88 95.7];
R = [765 790 826 850 873 910 942 980 1010 1022];
figure;
plot(t,R,"*");
hold on;
N = numel(t);
%最小二乘法拟合线性模型参数
den = N*sum(t.^2) - sum(t)^2;
a = (sum(R)*sum(t.^2) - sum(R.*t)*sum(t))/den
b = (N*sum(R.*t) - sum(R)*sum(t))/den
%绘制拟合直线
t1 = 1:100;
R1 = a + b*t1;
plot(t1, R1);
%计算温度t2 = 70对应的组织
t2 = 70;
R2 = a + b*t2补充：如果希望将数据点连接起来，可以将plot语句改成：plot(t,R,"*-");
输出结果如下：
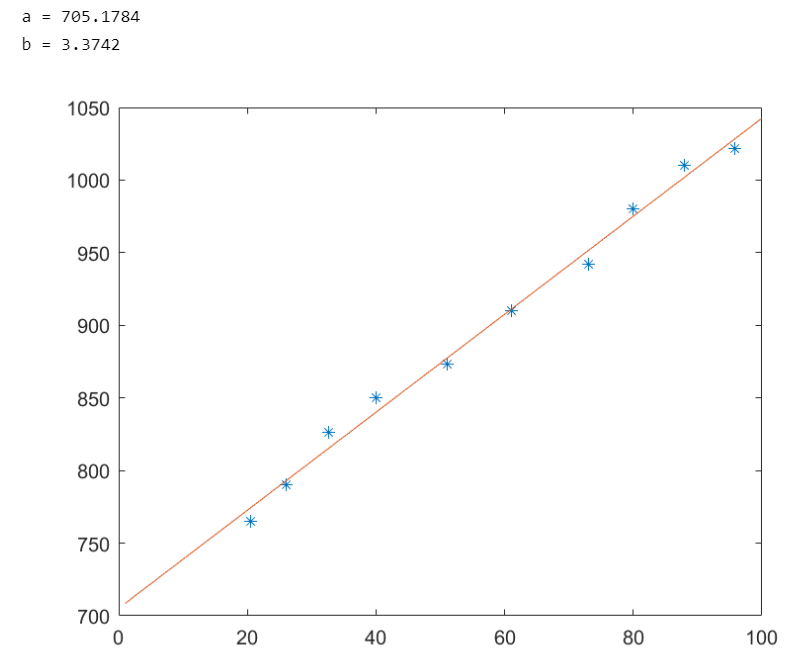
三、LSM在控制系统建模中的应用
算法原理：
注意事项：
伪随机序列（M序列）的产生：
matlab代码：
clear;
n = 4; %四个移位寄存器
L = 2^n-1; %M序列的周期
mag = 5; %M序列的幅值
y1 = 1; y2 = 1; y3 = 1; y4 = 0; %四个移位寄存器的初始值
for i = 1:L
x1 = xor(y3,y4);
x2 = y1;
x3 = y2;
x4 = y3;
y(i) = y4;
if y(i) > 0.5
u(i) = -mag;
else
u(i) = mag;
end
y1 = x1;
y2 = x2;
y3 = x3;
y4 = x4;
end
figure(1); stem(u); grid on;
title('输入如信号M序列')生成的信号如下：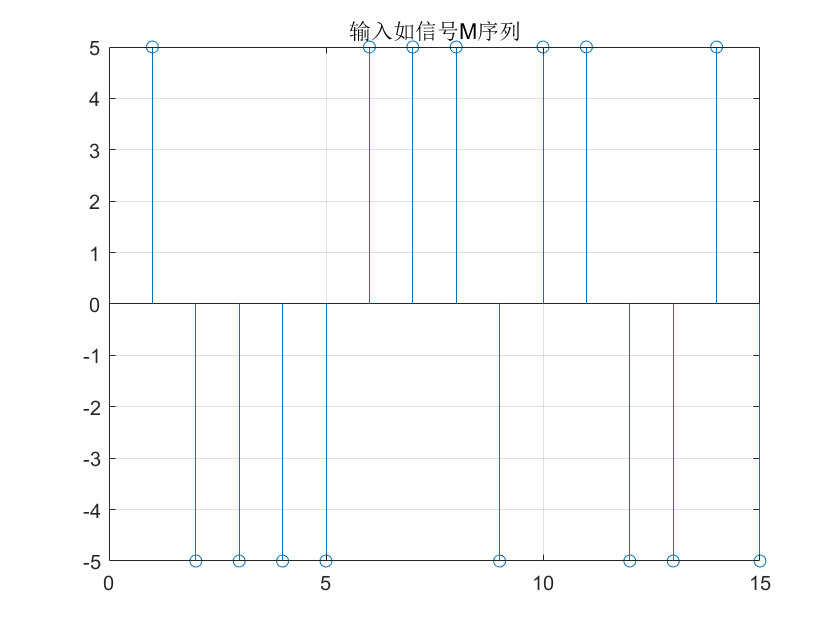
本文仅作为个人笔记使用，源自：Matlab系统辨识 - Yu_tiann - 博客园 (cnblogs.com)
https://www.cnblogs.com/yutian-blogs/p/15775734.html