简介
马拉车算法(Manacher Algorithm)于 1975 年被 Manacher(全名 Glenn K. Manacher)提出,该算法完美的解决了 O(n2)O(n^2)O(n2) 找最长回文串耗时久的特点。
算法作用
该算法主要是在 O(n)O(n)O(n) 的时间复杂度下解决了求最长回文串的问题。
概念引入
回文串:就是正着读和反着读都一样的字符串。
回文中心:回文串的对称中心,也是回文串的中点。
回文半径:回文中心到两端的距离。
举个例子:
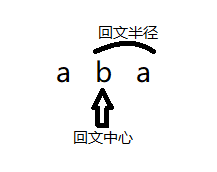
当然,有时是这样的情况:
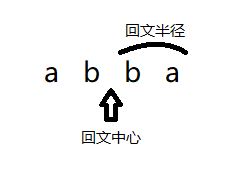
因此,对于回文串,我们通常会在字符之间加一个符号(比如加一个 #),当然,头和尾也要加:
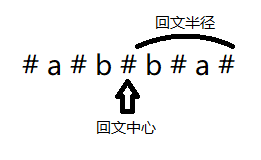
(上面那个同理,我就不过多说明了。)
算法讲解
首先先让我们回顾一下之前我们是怎么找最长回文串的:
找到一个字符,往两边拓展,直到没法再拓展。
这样就太费时间了,有没有办法通过已知信息来优化呢?
于是 Manacher 算法诞生了。
Manacher 的核心其实就一个:借助回文串的对称性用旧的更新新的。
具体怎么说呢?我们假设目前最靠右的回文串的回文中心是 c,r[c] 是以 c 为回文中心的最长回文半径:
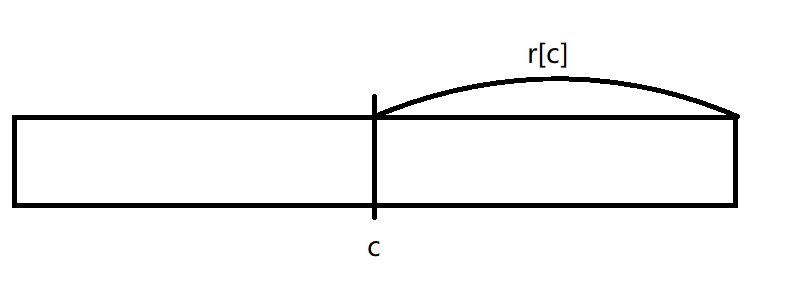
然后现在我们要更新 i 的最长回文半径(也就是 r[i]),那 c 肯定在 i 之前就被扫过了:
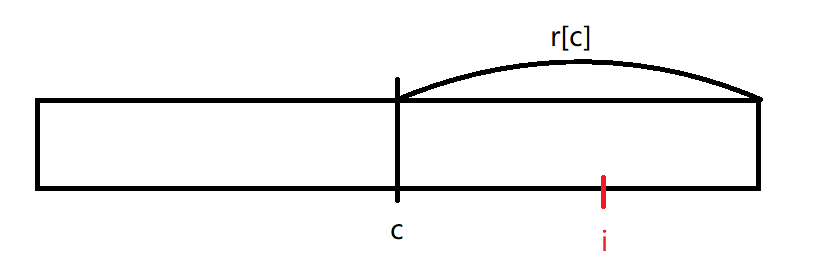
现在考虑 i 关于 c 的对称点 j:
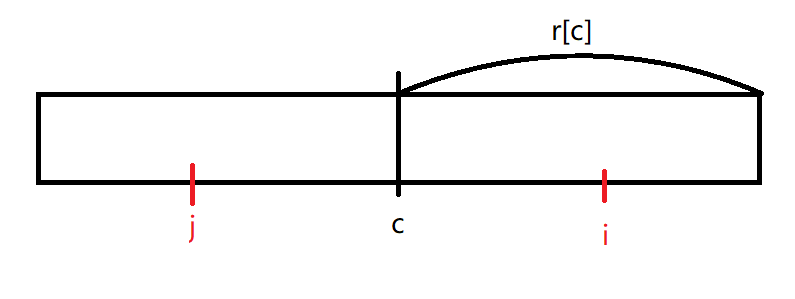
明显,我们已经知道了 r[j] 的大小,我们在图上表示出来:
氛围两种情况:
情况一
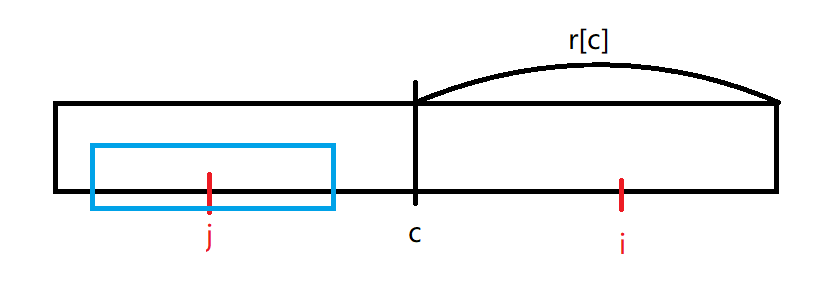
其中蓝色方框内就是以 j 为回文中心的回文串。
那么根据回文串的对称性,这个蓝色的方框应该也可以被翻过去:
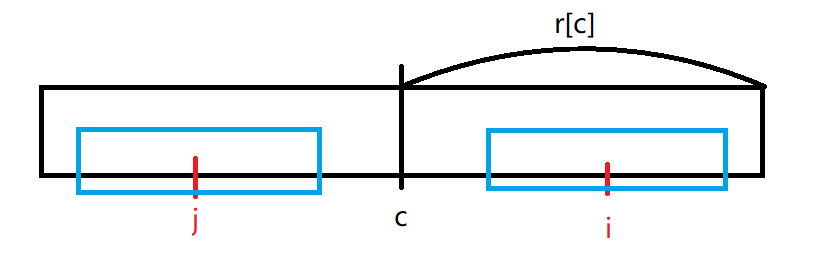
此时 r[i]=r[j],而 i+j2=c\cfrac{i+j}{2}=c2i+j=c,所以 j=2×c−ij=2\times c-ij=2×c−i。
第二种情况
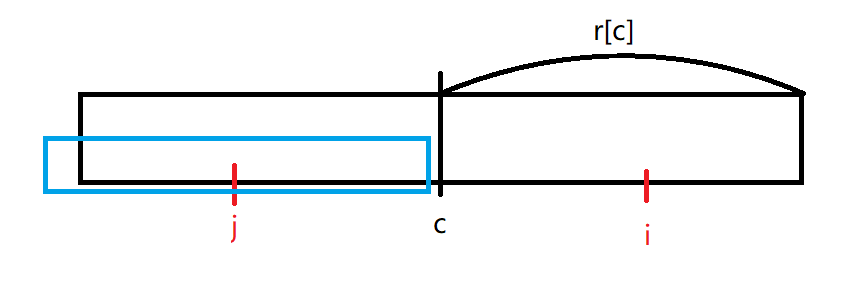
这个时候我们就不能直接翻过去了,因为我们前面说了:以 c 为回文中心的回文串是目前最靠右的回文串。这说明在 c+r[c] 后面的字符串跟前面的根本不一样,但是我们可以确定的是绿色方框内的这一部分一定一样:
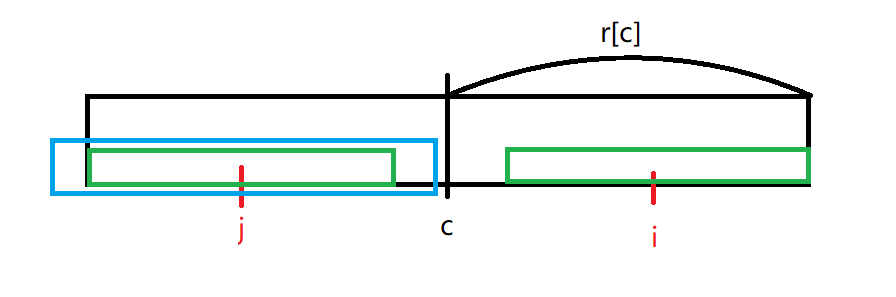
所以此时 r[i]=c+r[c]-i。
然后我们再暴力往两边拓展就行了。
核心代码:
cpp
cin>>s;
n=s.size();
ss+='#';
for(int i=0;i<n;i++)//在字符之间加一个 #
{
ss+=s[i];
ss+='#';
}
int c=0;
for(int i=0;i<2*n+1;i++)
{
if(i<c+r[c])//注意:这个点一定要在最靠右的回文串内,不然我们是不知道它的做优字符是什么的
{
r[i]=min(r[2*c-i],c+r[c]-i);//这里为了方便其实可以简写为取最小值
}
while(i>=r[i]&&ss[i-r[i]]==ss[i+r[i]])//暴力往两边拓展
{
r[i]++;
}
r[i]--;//最后出来的时候是一定会多算一位的,所以要减去
if(r[i]+i>r[c]+c)//随时更新 c
{
c=i;
}
}然后就没然后了。