- 二叉树最大宽度
已解答
中等
相关标签
相关企业
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
示例 1: 
输入:root = [1,3,2,5,3,null,9]
输出:4
解释:最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9) 。示例 2:

输入:root = [1,3,2,5,null,null,9,6,null,7]
输出:7
解释:最大宽度出现在树的第 4 层,宽度为 7 (6,null,null,null,null,null,7) 。示例 3:
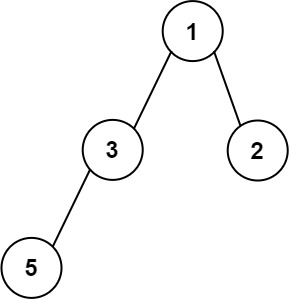
输入:root = [1,3,2,5]
输出:2
解释:最大宽度出现在树的第 2 层,宽度为 2 (3,2) 。解法一:
思路: 使用BFS的思想,依次把结点按照层序遍历存储到队列里面。由于题目说了需要空节点也要算进去,这里存储是我们应该存储【结点,结点在顺序表的位置】,采用字典即可。对于每层来说,只需找到每层第一个元素的位置和最后一个元素的位置,然后用end-start+1表示结果,遍历每一层结点,更新最大值,即可求得结果。

对于结点的编号,我们采用:根节点的编号是1(i),其左孩子结点的编号为2(2 *i),其右孩子的结点是3(2 *i+1)。如果遍历到空结点,我们就直接加入queue中,如果非空,我们就将孩子结点加入queue中,同时更新字典。
代码如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def widthOfBinaryTree(self, root):
"""
:type root: TreeNode
:rtype: int
"""
ans=0
node_index={}
queue=[root]
node_index[root]=1
while queue:
size=len(queue)
start=node_index[queue[0]]
while size:
size-=1
node=queue.pop(0)
index=node_index[node]
if node.left:
queue.append(node.left)
node_index[node.left]=2*index
if node.right:
queue.append(node.right)
node_index[node.right]=2*index+1
if size==0:
ans=max(ans,index-start+1)
return ans