LeetCode //C - 407. Trapping Rain Water II

407. Trapping Rain Water II

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

Example 1:

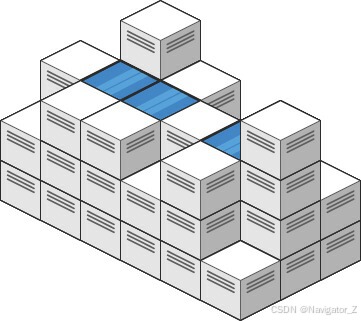
Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.

We have two small ponds 1 and 3 units trapped.

The total volume of water trapped is 4.

Example 2:

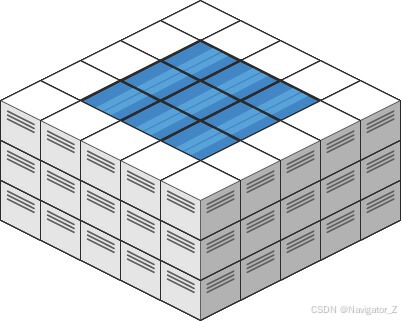
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

Constraints:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 < = h e i g h t M a p [ i ] [ j ] < = 2 ∗ 1 0 4 0 <= heightMap[i][j] <= 2 * 10^4 0<=heightMap[i][j]<=2∗104

From: LeetCode

Link: 407. Trapping Rain Water II

---

Solution:

Ideas:

1. Dynamic Min-Heap Implementation:

• A MinHeap structure is created to manage the elements in the heap. It includes functions for initializing the heap, inserting elements, and extracting the minimum element.
• The capacity of the heap is doubled whenever it is full, avoiding the issues of insufficient space.

2. Element Structure:

• The Element structure is used to store the coordinates and height of each cell.

3. Boundary Processing:

• The code ensures boundary cells are added to the heap correctly and avoids overwriting memory by properly managing the heap size.

4. Clean-up:

• Proper memory deallocation is done to avoid memory leaks.

Code:

typedef struct {
    int x, y;
    int height;
} Element;

typedef struct {
    Element *elements;
    int size;
    int capacity;
} MinHeap;

void initMinHeap(MinHeap *heap, int capacity) {
    heap->elements = (Element *)malloc(sizeof(Element) * capacity);
    heap->size = 0;
    heap->capacity = capacity;
}

void swap(Element *a, Element *b) {
    Element temp = *a;
    *a = *b;
    *b = temp;
}

void insertMinHeap(MinHeap *heap, Element element) {
    if (heap->size == heap->capacity) {
        heap->capacity *= 2;
        heap->elements = (Element *)realloc(heap->elements, sizeof(Element) * heap->capacity);
    }
    heap->elements[heap->size] = element;
    int i = heap->size++;
    while (i > 0) {
        int parent = (i - 1) / 2;
        if (heap->elements[i].height < heap->elements[parent].height) {
            swap(&heap->elements[i], &heap->elements[parent]);
            i = parent;
        } else {
            break;
        }
    }
}

Element extractMin(MinHeap *heap) {
    Element minElement = heap->elements[0];
    heap->elements[0] = heap->elements[--heap->size];
    int i = 0;
    while (true) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int smallest = i;
        if (left < heap->size && heap->elements[left].height < heap->elements[smallest].height) {
            smallest = left;
        }
        if (right < heap->size && heap->elements[right].height < heap->elements[smallest].height) {
            smallest = right;
        }
        if (smallest == i) {
            break;
        }
        swap(&heap->elements[i], &heap->elements[smallest]);
        i = smallest;
    }
    return minElement;
}

bool isInBounds(int x, int y, int m, int n) {
    return x >= 0 && x < m && y >= 0 && y < n;
}

int trapRainWater(int** heightMap, int heightMapSize, int* heightMapColSize) {
    if (heightMapSize == 0 || *heightMapColSize == 0) {
        return 0;
    }

    int m = heightMapSize;
    int n = *heightMapColSize;
    int totalWater = 0;

    bool **visited = (bool **)malloc(m * sizeof(bool *));
    for (int i = 0; i < m; i++) {
        visited[i] = (bool *)malloc(n * sizeof(bool));
        for (int j = 0; j < n; j++) {
            visited[i][j] = false;
        }
    }

    MinHeap heap;
    initMinHeap(&heap, m * n);

    // Add all boundary cells to the min-heap
    for (int i = 0; i < m; i++) {
        visited[i][0] = true;
        visited[i][n - 1] = true;
        insertMinHeap(&heap, (Element){i, 0, heightMap[i][0]});
        insertMinHeap(&heap, (Element){i, n - 1, heightMap[i][n - 1]});
    }
    for (int j = 0; j < n; j++) {
        visited[0][j] = true;
        visited[m - 1][j] = true;
        insertMinHeap(&heap, (Element){0, j, heightMap[0][j]});
        insertMinHeap(&heap, (Element){m - 1, j, heightMap[m - 1][j]});
    }

    int directions[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    
    // Process the heap
    while (heap.size > 0) {
        Element current = extractMin(&heap);
        int x = current.x;
        int y = current.y;
        int currentHeight = current.height;

        for (int j = 0; j < 4; j++) {
            int nx = x + directions[j][0];
            int ny = y + directions[j][1];
            
            if (isInBounds(nx, ny, m, n) && !visited[nx][ny]) {
                visited[nx][ny] = true;
                // Calculate the water that can be trapped
                if (currentHeight > heightMap[nx][ny]) {
                    totalWater += currentHeight - heightMap[nx][ny];
                }
                // Add the neighbor to the heap with the maximum height
                insertMinHeap(&heap, (Element){nx, ny, heightMap[nx][ny] > currentHeight ? heightMap[nx][ny] : currentHeight});
            }
        }
    }

    // Clean up
    for (int i = 0; i < m; i++) {
        free(visited[i]);
    }
    free(visited);
    free(heap.elements);

    return totalWater;
}