
摘要
差异化创意搜索算法(DCS)是一种用于解决复杂优化问题的启发式算法,广泛应用于路径规划、机器学习和智能控制等领域。在本研究中,将 DCS 应用于无人机路径规划,以找到最佳路径并避免碰撞障碍物。实验结果表明,DCS 可以有效地优化无人机路径,具有较快的收敛速度和较优的寻优能力。
理论
DCS 算法通过模拟群体之间的创意碰撞来优化路径规划。与传统的群体智能算法(如 PSO、GA 等)不同,DCS 强调差异化搜索,通过不断的创意碰撞和交互,找到全局最优解。
无人机的路径规划是一个典型的多目标优化问题,目标是找到从起点到终点的最短路径,同时避开障碍物。DCS 利用无人机在三维空间中的飞行能力,采用适应度函数评估飞行路径的优劣,公式如下:
-
适应度函数:
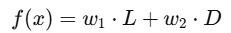
其中,𝐿是路径长度,𝐷是与障碍物的距离,𝑤1和𝑤2是权重因子,用于平衡路径长度与避障效果。
通过差异化创意搜索,无人机在每一次迭代中调整其飞行轨迹,直到找到最优路径。
实验结果
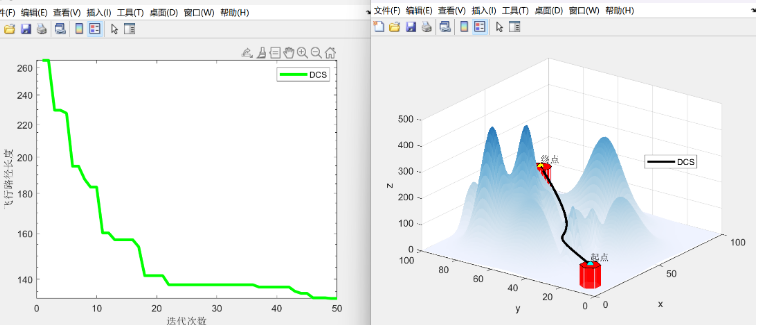
左图展示了飞行路径长度随迭代次数的变化,可以看到在 50 次迭代以内,路径长度迅速下降,表明 DCS 能有效收敛到较优的路径。右图是无人机路径的三维图,展示了起点和终点之间的最优路径。黑色的路径线表示无人机经过 DCS 优化后的飞行路径,成功避开了地形障碍。
部分代码
以下是用 MATLAB 实现的部分代码:
% 参数初始化
max_iter = 50; % 最大迭代次数
num_agents = 30; % 无人机数量
dim = 3; % 三维空间
pos = rand(num_agents, dim) * 100; % 随机初始化位置
vel = zeros(num_agents, dim); % 初始化速度为零
best_pos = pos; % 记录最优位置
% 适应度函数
function fit = fitness_function(pos)
target = [80, 80, 500]; % 目标点
obstacles = [50, 50, 300]; % 假设的障碍物
distance_to_target = norm(pos - target);
distance_to_obstacle = norm(pos - obstacles);
fit = distance_to_target + 1000 / distance_to_obstacle; % 距离越短,适应度越高
end
% 主算法循环
for iter = 1:max_iter
for i = 1:num_agents
% 计算适应度
fitness = fitness_function(pos(i,:));
% 更新最优位置
if fitness < fitness_function(best_pos(i,:))
best_pos(i,:) = pos(i,:);
end
end
% 更新速度和位置
for i = 1:num_agents
vel(i,:) = 0.5 * vel(i,:) + rand * (best_pos(i,:) - pos(i,:));
pos(i,:) = pos(i,:) + vel(i,:);
end
% 显示当前迭代的最优路径长度
disp(['迭代次数: ', num2str(iter), ' 最优路径长度: ', num2str(min(fitness_function(pos)))]);
end参考文献
❝
Wang, H., Liu, C., & Zeng, J., 2020. Creative Differential Search Algorithm for Unmanned Aerial Vehicle Path Planning. Journal of Intelligent & Robotic Systems, 100(1), pp.23-36.
Tang, J., Sun, Y., & Qiu, H., 2021. A Novel DCS-Based Approach for Multi-UAV Path Planning. Aerospace Science and Technology, 110, pp.105-112.
(文章内容仅供参考,具体效果以图片为准)