标定目的:建立相机成像几何模型并矫正透镜畸变。
- 建立相机成像几何模型:计算机视觉的首要任务就是要通过拍摄到的图像信息获取到物体在真实三维世界里相对应的信息,于是,建立物体从三维世界映射到相机成像平面这一过程中的几何模型就显得尤为重要,而这一过程最关键的部分就是要得到相机的内参和外参。
- 矫正透镜畸变:我们最开始接触到的成像方面的知识应该是有关小孔成像的,但是由于这种成像方式只有小孔部分能透过光线就会导致物体的成像亮度很低,于是聪明的人类发明了透镜。虽然亮度问题解决了,但是新的问题又来了:由于透镜的制造工艺,会使成像产生多种形式的畸变,于是为了去除畸变(使成像后的图像与真实世界的景象保持一致),人们计算并利用畸变系数来矫正这种像差。虽然理论上可以设计出不产生畸变的透镜,但其制造工艺相对于球面透镜会复杂很多,所以相对于复杂且高成本的制造工艺,人们更喜欢用数学来解决问题。
双目标定包含的两个内容:
(1)左目和右目各自内参和畸变系数的标定(单目标定)
(2)两台相机之间相互位置的标定(双目标定)
因为在许多三维重建算法(将二维图像转换为三维空间模型的技术)中,我们都要知道两台相机之间的相对位置关系,这样才能进行距离计算。
双目标定前后,双目模型对比如下图所示:
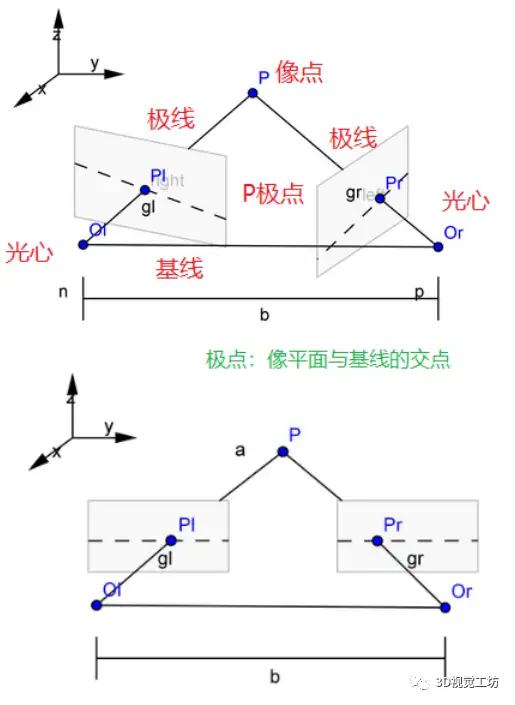
概念如下:
基线:两个光心的连线称为基线
极平面:物点(空间点M)与两个光心的连线构成的平面称为极平面;
极线:极平面与成像平面的交线
极点:极线的一端,基线与像平面的交点
像点:极线的一端,光心与物点连线与像平面的交点;
可以看出:
校正前,相机的光心不是相互平行的
校正后,极点在无穷远处,两个相机的光轴平行,像点在左右图像上的高度一致
标定+校正后图片:

图2 立体校正后左右相机图像发生一定扭曲
这样做的好处是:比如后续的立体匹配时,只需在同一行上搜索左右像平面的匹配点即可,能使效率大大提高。所以,我们要知道右相机相对于左相机的位姿关系,那我们才可以做校正。
单目相机标定理论
相机成像原理
相机成像系统中,共包含四个坐标系:世界坐标系、相机坐标系、图像坐标系、像素坐标系。
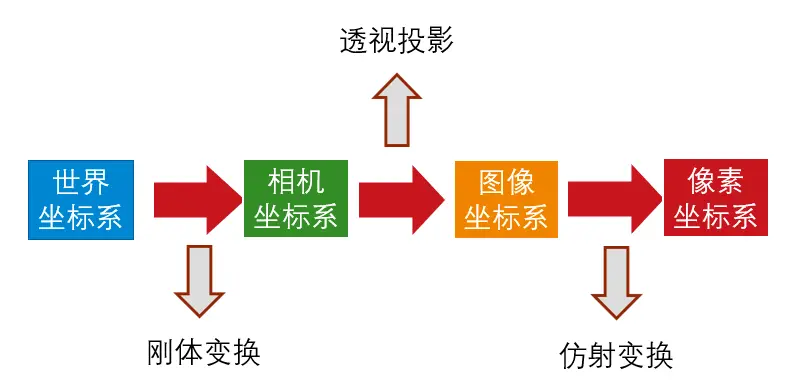
这四个坐标系之间的转化关系为:
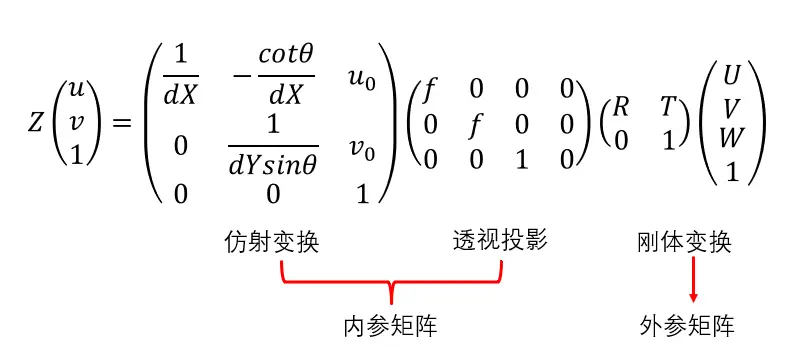
其中, (U ,V ,W )为在世界坐标系下一点的物理坐标, (u ,v )为该点对应的在像素坐标系下的像素坐标, Z为尺度因子。
我们将矩阵:
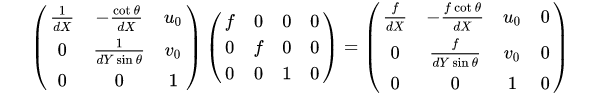
称为相机的内参矩阵,内参矩阵取决于相机的内部参数。其中, f 为像距, dX , dY 分别表示X ,Y 方向上的一个像素在相机感光板上的物理长度(即一个像素在感光板上是多少毫米), u 0,v 0 分别表示相机感光板中心在像素坐标系下的坐标, θ 表示感光板的横边和纵边之间的角度( 90°表示无误差)。
我们将矩阵:
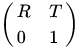
称为相机的外参矩阵,外参矩阵取决于相机坐标系和世界坐标系的相对位置, R 表示旋转矩阵, T 表示平移矢量。
即单点无畸变的相机成像模型如下:
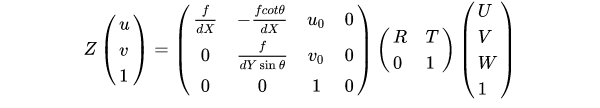
因此,相机标定的第一个目的就是获得相机的内参矩阵和外参矩阵。
畸变与畸变矫正
另外,相机拍摄的图片还存在一定的畸变,畸变包括桶形畸变和枕形畸变。畸变模型包括径向畸变和切向畸变。
畸变公式(3阶)如下:
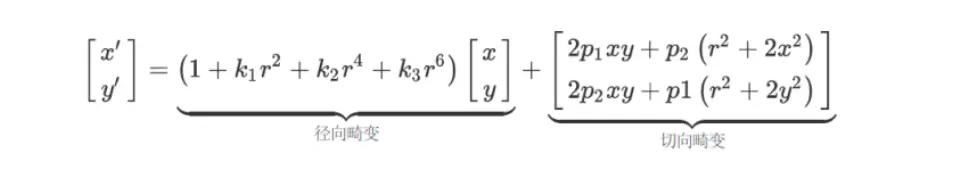
其中, (x,y),(x′,y′) 分别为理想的无畸变的归一化的图像坐标、畸变后的归一化图像坐标,
r 为图像像素点到图像中心点的距离,即 
相机标定的第二个目的就是获得相机的畸变参数,如上式中的 k 1, k 2, p 1, p2等,进而对拍摄的图片进行去畸变处理。
张正友标定法
张正友标定法利用如下图所示的棋盘格标定板,在得到一张标定板的图像之后,可以利用相应的图像检测算法得到每一个角点的像素坐标 (u ,v)。
张正友标定法将世界坐标系固定于棋盘格上,则棋盘格上任一点的物理坐标 W =0,由于标定板的世界坐标系是人为事先定义好的,标定板上每一个格子的大小是已知的,我们可以计算得到每一个角点在世界坐标系下的物理坐标 (U ,V ,W=0)。
我们将利用这些信息:每一个角点的像素坐标 (u ,v )、每一个角点在世界坐标系下的物理坐标 (U ,V ,W =0),来进行相机的标定,获得相机的内外参矩阵、畸变参数。
