针对考研的C语言学习（二叉树专题）

二叉树层次建树

对于二叉树，建树过程中需要一个（尾插法的）链表（或队列）来辅助确认当前父亲节点

由于尾插法需要一个尾指针。因此可以理解为队列，只不过是不带头结点的链表版队列。

但其实就是一个辅助找到当前父亲节点的作用，不必纠结是啥名字。

代码如下：

#include<stdio.h>
#include<stdlib.h>
typedef char ElemType;
//树结构体
typedef struct tree_node{
  ElemType val;
  struct tree_node*lc;
  struct tree_node*rc;
}Tnode,*BTree;

//链表
typedef struct link{
  BTree tree;//存储的是树的节点
  struct link*next;
}LinkNode,*LinkList;

void build_tree(BTree&tree,LinkList&front,LinkList& rear)
{
    //还需要一个指向当前父亲节点的指针
    LinkList cur = NULL;
    ElemType data;
    while(scanf("%c",&data) && data != '\n')
    {
        //每次来一个新建一个树的节点和链表的节点
        BTree newTree = (BTree)calloc(1,sizeof(Tnode));
        LinkList newList = (LinkList)calloc(1,sizeof(LinkNode));
        newTree->val = data;
        newList->tree=newTree;
        //进行判读是不是父亲节点
        if(tree == NULL)
        {
            tree = newTree;
            //入队
            front = rear = newList;
            cur=rear;
        }
        else
        {
            if(cur->tree->lc == NULL)
            {
                //插入左子树
                cur->tree->lc=newTree;
                //入队并更新尾指针
                rear->next=newList;
                rear = rear->next;
            }
            else
            {
                cur->tree->rc = newTree;
                //入队并更新尾指针
                rear->next=newList;
                rear = rear->next;
                //注意这里左右子树都满了，当前父亲节点要换
                cur= cur->next;
            }
        }
    }
}

//前序便利
void pre_print(BTree tree)
{
    if(tree)
    {
        putchar(tree->val);
        pre_print(tree->lc);
        pre_print(tree->rc);
    }
}
void mid_print(BTree tree)
{
    if(tree)
    {
        //左跟右
        mid_print(tree->lc);
        putchar(tree->val);
        mid_print(tree->rc);
    }
}
void post_print(BTree tree)
{
    if(tree)
    {
        //左右跟
        post_print(tree->lc);
        post_print(tree->rc);
        putchar(tree->val);
    }
}
int main()
{
    BTree tree = NULL;//树根
    LinkList front=NULL;
    LinkList rear=NULL;//需要用到尾插法
    build_tree(tree,front,rear);
    pre_print(tree);
    puts("");
    mid_print(tree);
    puts("");
    post_print(tree);
	return 0;
}

前序便利：根左右--->先打印自身再左子树再右子树

//前序便利
void pre_print(BTree tree)
{
    if(tree)
    {
        putchar(tree->val);
        pre_print(tree->lc);
        pre_print(tree->rc);
    }
}

中序遍历：左根右--->先打印左子树再打印自身再右子树

void mid_print(BTree tree)
{
    if(tree)
    {
        //左跟右
        mid_print(tree->lc);
        putchar(tree->val);
        mid_print(tree->rc);
    }
}

后序遍历：左右根--->先打印左子树再右子树再自身

void post_print(BTree tree)
{
    if(tree)
    {
        //左右跟
        post_print(tree->lc);
        post_print(tree->rc);
        putchar(tree->val);
    }
}

【注意】以上三中便利采用递归思想。

代码运行结果如下

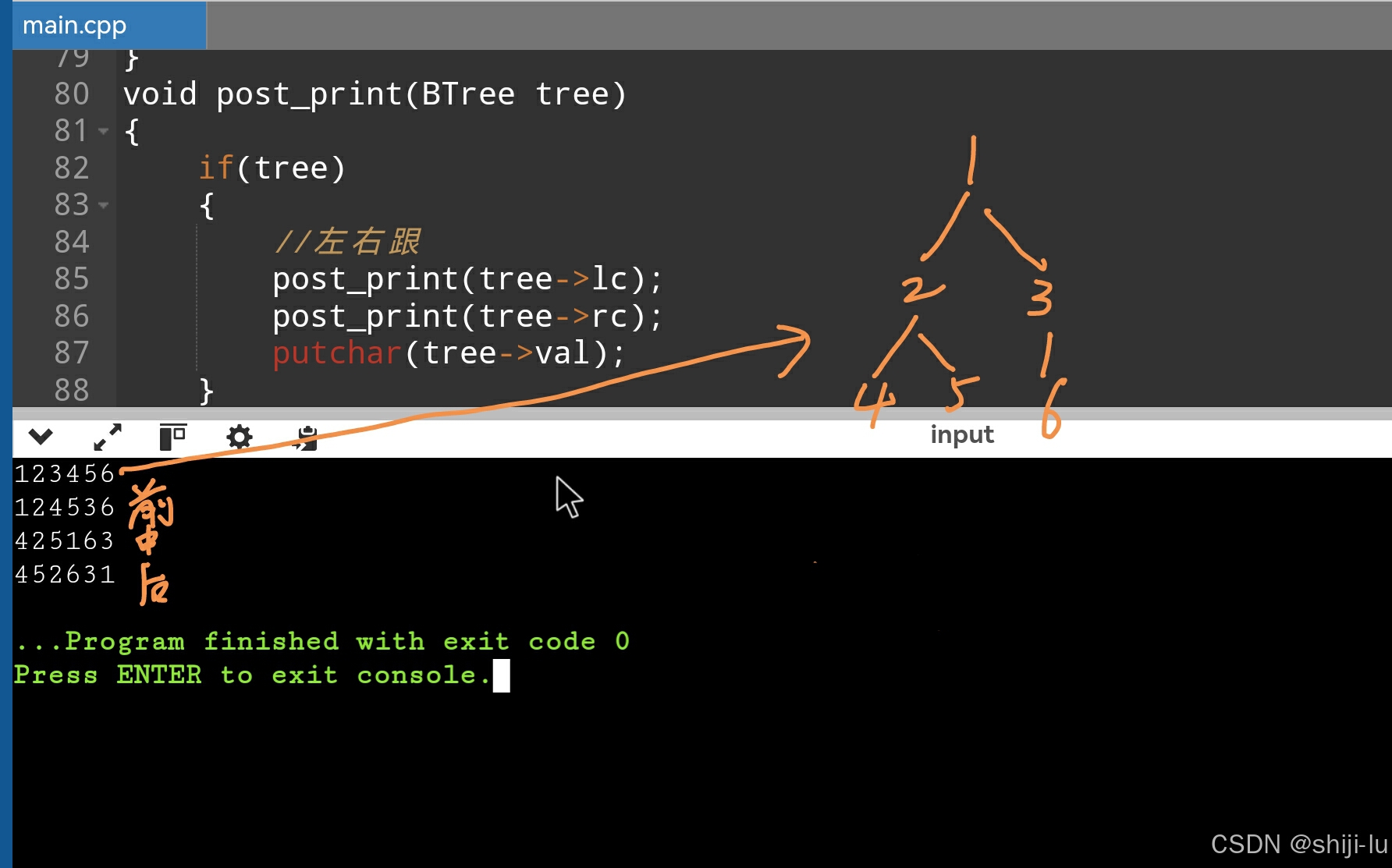
封装思想展示，队列封装

#include<stdio.h>
#include<stdlib.h>
typedef char ElemType;

//树
typedef struct trees{
    ElemType data;
    struct trees*lc;
    struct trees*rc;
}treeNode,*Tree;

//链表
typedef struct Links{
    Tree tree;
    struct Links*next;
}LNode,*LinkList;

//队列
typedef struct{
  LinkList front;
  LinkList rear;
}LinkQue;

void init_que(LinkQue&q)
{
    q.front=q.rear=(LinkList)calloc(1,sizeof(LNode));
    q.front=q.rear;
}

bool isEmpty(LinkQue&q)
{
    return q.front == q.rear;
}

//入队
void push_que(LinkQue&q,Tree tree)
{
    //新建链表节点
    LinkList newList = (LinkList)calloc(1,sizeof(LNode));
    newList->next=NULL;
    newList->tree=tree;
    q.rear->next=newList;
    q.rear=q.rear->next;
}
bool pop_que(LinkQue&q,Tree &tree)
{
    if(isEmpty(q))
    {
        return false;
    }
    LinkList del = q.front->next;//头结点不存数据，第一个节点才是真的数据起始位置
    q.front->next=del->next;//断链
    tree=del->tree;
    if(q.rear == del)//只剩下尾节点的数据
    {
        q.rear=q.front;//置空
    }
    free(del);
    return true;
}

void build_tree(Tree&tree)
{
    LinkQue q;
    init_que(q);
    LinkList cur = NULL;
    ElemType data;
    while(scanf("%c",&data) && data != '\n')
    {
        Tree newTree = (Tree)calloc(1,sizeof(treeNode));//申请新的树的节点
        newTree->data=data;
        if(tree == NULL)
        {
            tree = newTree;
            push_que(q,tree);//入队
            cur = q.rear;
        }
        else
        {
            if(cur->tree->lc == NULL)
            {
                cur->tree->lc = newTree;
                push_que(q,newTree);
            }
            else
            {
                cur->tree->rc = newTree;
                push_que(q,newTree);
                //改变当前父亲节点
                cur = cur->next;
            }
        }
    }
}

void pre_print(Tree t)
{
    if(t)
    {
        putchar(t->data);
        pre_print(t->lc);
        pre_print(t->rc);
    }
}
void mid_print(Tree t)
{
    if(t)
    {
        mid_print(t->lc);
        putchar(t->data);
        mid_print(t->rc);
    }
}
void post_print(Tree t)
{
    if(t)
    {
        post_print(t->lc);
        post_print(t->rc);
        putchar(t->data);
    }
}


int main()
{
    Tree tree = NULL;
    build_tree(tree);
    // pre_print(tree);
  
    return 0;
}

层次遍历在下节