AcWing272

AcWing 272. 最长公共上升子序列【LCIS + 优化】 - AcWing

这题结合了 LCS（最长公共子序列） 和 LIS（最长递增子序列） 的思想，用动态规划解决两个序列之间的匹配与递增关系。

问题思路：

这道题结合了 LIS（最长上升子序列） 和 LCS（最长公共子序列） 两种思想，求解两个数组中的最长公共上升子序列。所以DP设计上也是两者的结合。

DP 分析：

1. 初始化：

   • 使用二维数组 f[i][j]，表示考虑数组 a 的前 i 个数字和数组 b 的前 j 个数字，且以 b[j] 结尾的 LCIS 的最大长度。

2. 状态转移：

   

   

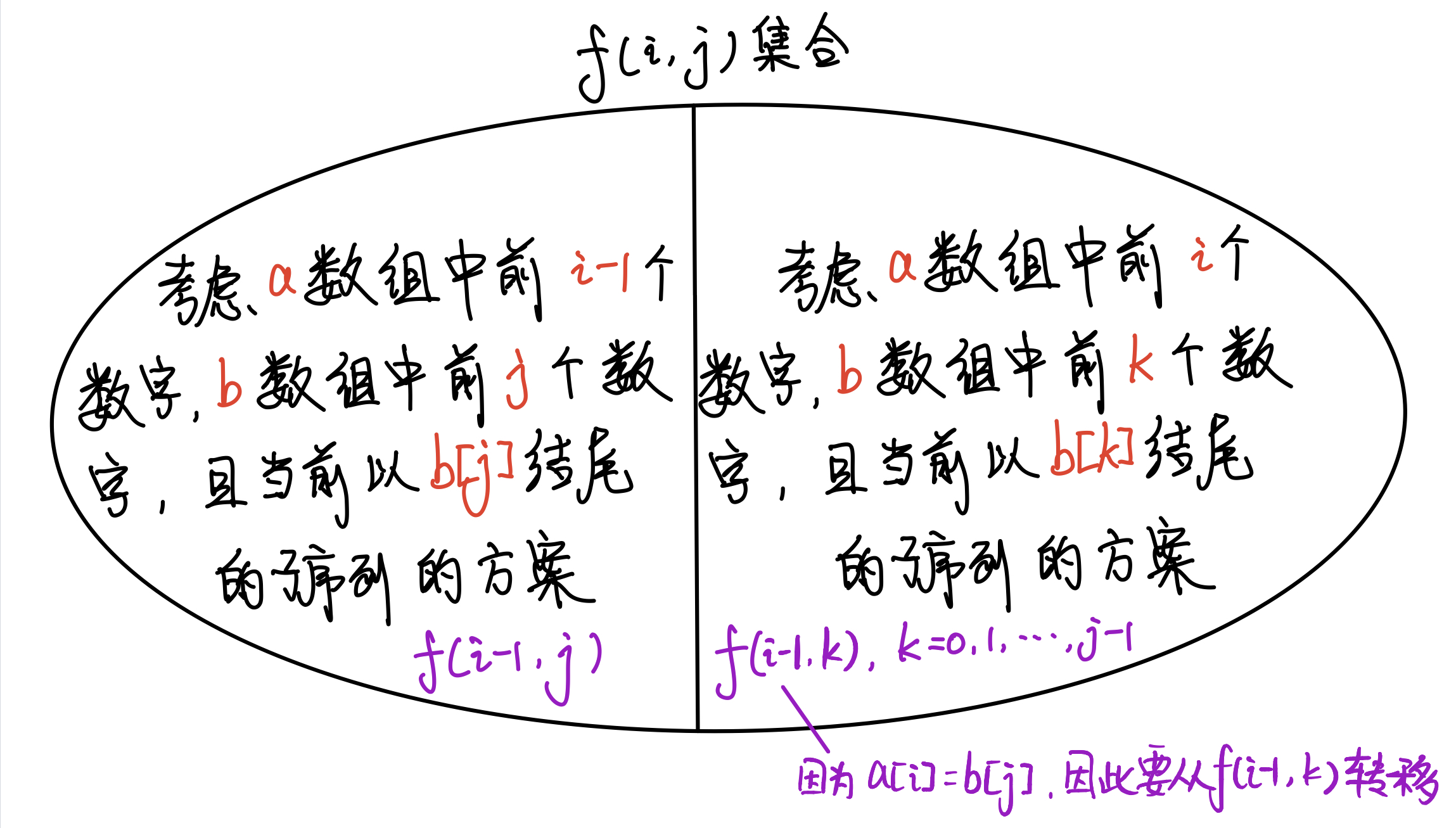
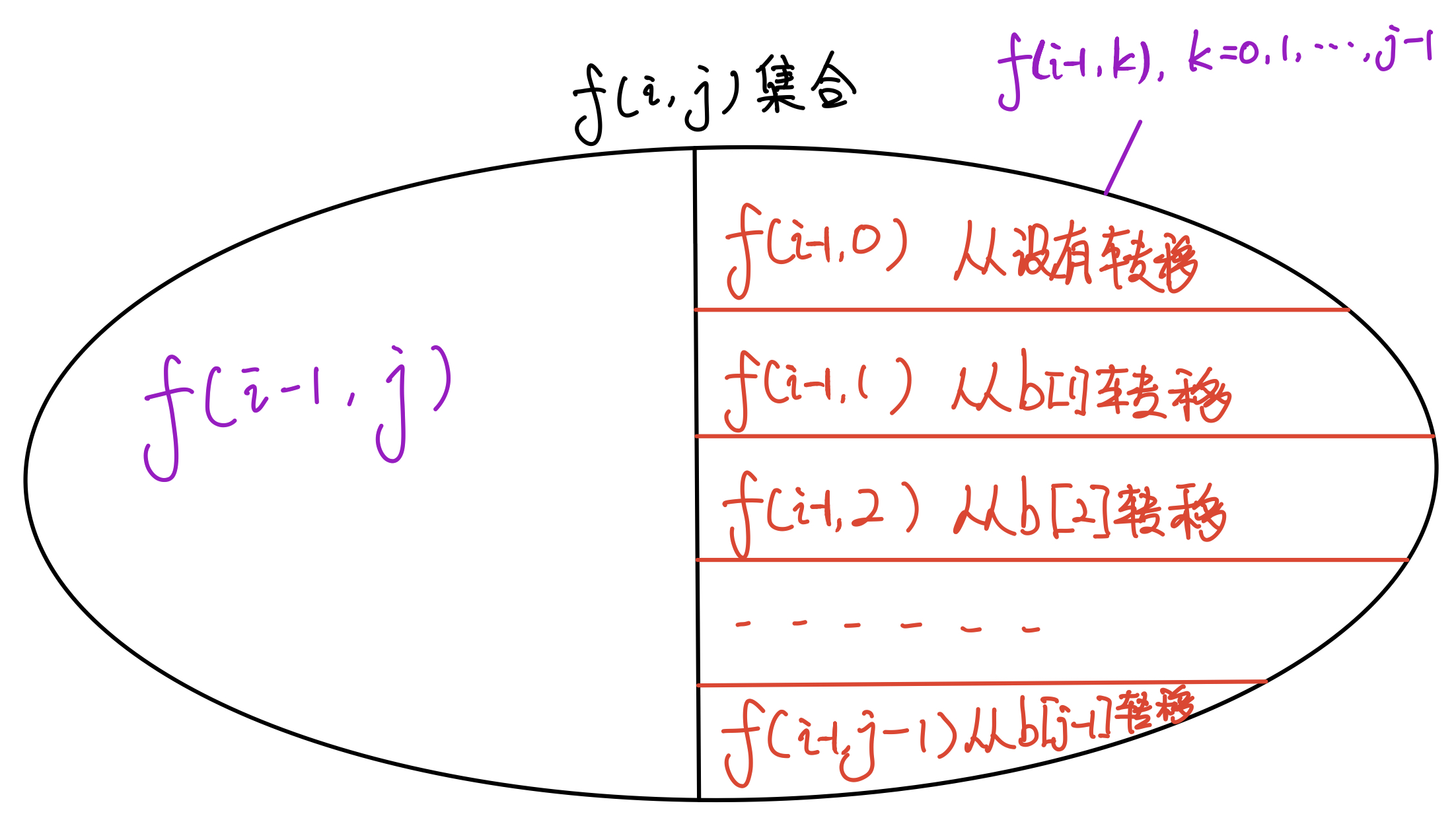
3. 目标状态 ：

   计算所有 f[n][j] 中的最大值，即为最终 LCIS 的长度。

代码

作者：一只野生彩色铅笔
链接：https://www.acwing.com/solution/content/52304/
来源：AcWing
#include <iostream>

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];

int main()
{
    //input
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> a[i];
    for (int i = 1; i <= n; ++ i) cin >> b[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 1; j <= n; ++ j)
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j])
            {
                for (int k = 0; k < j; ++ k)
                {
                    if (b[j] > b[k])
                    {
                        f[i][j] = max(f[i][j], f[i - 1][k] + 1);
                    }
                }
            }
        }
    }

    //find result
    int res = 0;
    for (int i = 0; i <= n; ++ i) res = max(res, f[n][i]);
    cout << res << endl;

    return 0;
}