day01 数组
Java JDK是17.0.11
35 34 69 367
26 283 844 977
904 76
54 剑指offer 29
1 数组理论基础
数组是存放在连续内存空间上的相同类型数据的集合。
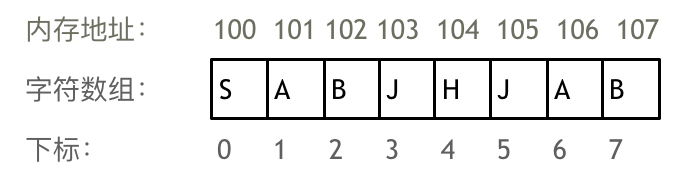
数组下标都是从0开始的。
数组内存空间的地址是连续的。
因为数组在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。
例如删除下标为3的元素,需要对下标为3的元素后面的所有元素都要做移动操作。

数组的元素是不能删的,只能覆盖。
Java:二维数组在内存中不是连续的,每个子数组是独立的对象。
java
public class FundamentalsTheory {
public static void main(String[] args) {
testArr();
}
public static void testArr(){
//初始化二维数组
int[][] arr=new int[2][3];
arr[0]=new int[]{1,2,3};
arr[1]=new int[]{4,5,6};
//输出地址
for(int i=0;i< arr.length;i++){
System.out.println("Subarray " + i + ": " + System.identityHashCode(arr[i]));
for(int j=0;j<arr[i].length;j++){
System.out.println(System.identityHashCode(arr[i][j])+" ");
}
System.out.println();
}
}
}
java
Subarray 0: 1324119927
1607521710
363771819
2065951873
Subarray 1: 1791741888
1595428806
1072408673
1531448569 Java:二维数组在内存中不是连续的,每个子数组是独立的对象。
2 二分查找法
区间定义,一般是左闭右闭,左闭右开。
左闭右闭
java
package com.jiangxun.array;
/**
* @author jiangxun
*/
public class BinarySearch {
/**
* leetcode27
* 左闭右闭
* while(left<=right) 小于等于 当 left=right [1,1] 区间合法。 mid=left+(right-left)/2。target是我们的目标值
* if(nums[mid] > target),nums[mid]不等于target,我的搜索区间包含right,而nums[mid]确定不是target,right = mid-1。
* if(nums[mid] < target),nums[mid]不等于target,我的搜索区间包含left,而nums[mid]确定不是target,left = mid+1。
* if(nums[mid] = target)返回mid。否则返回-1;
* 左闭右开
* 注意right=nums.length
* while(left < right) 小于 当 left=right [1,1) 区间不合法。mid=left+(right-left)/2。target是我们的目标值
* if(nums[mid] > target),nums[mid]不等于target,我的搜索区间不包含right,right = mid。
* if(nums[mid] < target),nums[mid]不等于target,我的搜索区间包含left,所以left = mid+1。
*/
public static void main(String[] args) {
int[] nums = {1, 2, 3, 4, 5};
int target1 = 3;
int target2 = 4;
int result1 = search1(nums, target1);
int result2 = search2(nums, target2);
System.out.println("Index of " + target1 + " is: " + result1);
System.out.println("Index of " + target2 + " is: " + result2);
}
public static int search1(int[] nums, int target) {
int left=0;
int right=nums.length-1;
while(left<=right){
int mid=left+(right-left)/2;
if (nums[mid]>target){
right=mid-1;
}
else if(nums[mid]<target){
left=mid+1;
}
else{
return mid;
}
}
//没找到
return -1;
}
public static int search2(int[] nums, int target) {
int left=0;
//注意数组区间个数
int right=nums.length;
while(left<right){
int mid=left+(right-left)/2;
if (nums[mid]>target){
right=mid;
}
else if(nums[mid]<target){
left=mid+1;
}
else{
return mid;
}
}
//没找到
return -1;
}
}
//时间复杂度:O(log n)
//空间复杂度:O(1)3 移除元素
plain
package com.jiangxun.array;
/**
* @author jiangxun
*/
public class RemoveElement {
public static void main(String[] args) {
int[] nums = {3, 2, 2, 3};
int val = 3;
// int result1 = removeElement1(nums, val);
// System.out.println("New length: " + result1);
int result2 = removeElement2(nums, val);
System.out.println("New length: " + result2);
}
/**
* leetcode27
* 移除数组中值为val的元素,返回 nums 中与 val 不同的元素的数量。
* 快指针用来获取新数组中的元素,慢指针用来获取新数组中需要更新的位置
* @param nums
* @param val
* @return
*/
public static int removeElement1(int[] nums, int val) {
int fast=0;
int slow=0;
while(fast<nums.length){
if(nums[fast]!=val){
nums[slow]=nums[fast];
slow++;
}
fast++;
}
return slow;
}
/**
* 双向指针移动 一个指针从左向右移动,另一个指针从右向左移动,如果左指针指向的元素等于val,
* 则将右指针指向的元素赋值给左指针指向的元素,右指针向左移动。
* @param nums
* @param val
* @return
*/
public static int removeElement2(int[] nums, int val) {
int left=0;
int right=nums.length-1;
while(left<=right){
if(nums[left]==val){
nums[left]=nums[right];
right--;
}else{
left++;
}
}
return left;
}
}4 平方数
plain
package com.jiangxun.array;
import java.util.Arrays;
/**
* @author jiangxun
*/
public class SortedSquares {
public static void main(String[] args)
{
int[] nums = {-4,-1,0,3,10};
// int[] result = sortedSquares1(nums);
int[] result = sortedSquares2(nums);
for (int i : result)
{
System.out.println(i);
}
}
/**
* 977 终于碰到简单的题了!
* @param nums
* @return
*/
public static int[] sortedSquares1(int[] nums){
for (int i = 0; i < nums.length; i++) {
nums[i] = nums[i] * nums[i];
}
Arrays.sort(nums);
return nums;
}
/**
* 初始化结果数组 result,长度与输入数组相同。
* 使用两个指针 left 和 right 分别指向数组的起始和末尾。
* 使用 pos 指向结果数组的末尾。
* 在 while 循环中,比较 left 和 right 所指元素的平方值,将较大的平方值放入结果数组的 pos 位置,并移动相应的指针。
* 重复上述步骤,直到所有元素都被处理完。
* 返回结果数组。
* @param nums
* @return
*/
public static int[] sortedSquares2(int[] nums) {
int n = nums.length;
int[] result = new int[n];
int left = 0;
int right = n - 1;
int pos = n - 1;
while (left <= right) {
int leftSquare = nums[left] * nums[left];
int rightSquare = nums[right] * nums[right];
if (leftSquare > rightSquare) {
result[pos] = leftSquare;
left++;
} else {
result[pos] = rightSquare;
right--;
}
pos--;
}
return result;
}
}day02 数组
1 长度最小的子数组
介绍数组操作中另一个重要的方法:滑动窗口。
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢。
首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置。
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
那么问题来了, 滑动窗口的起始位置如何移动呢?
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:
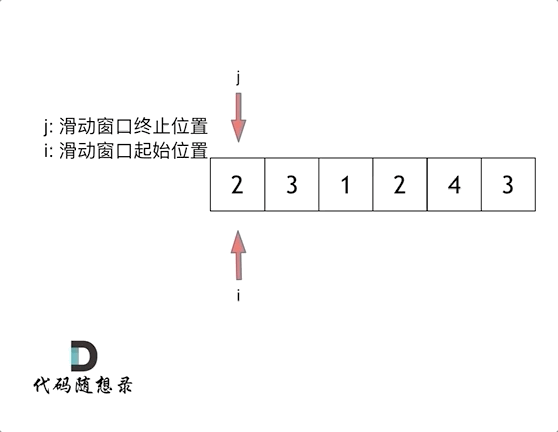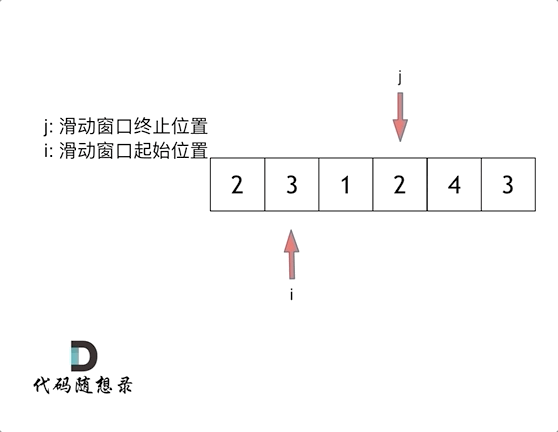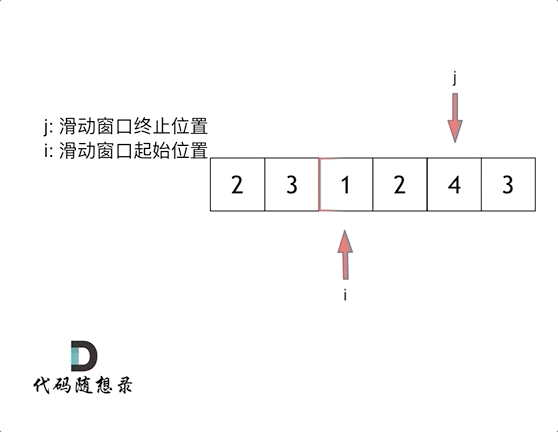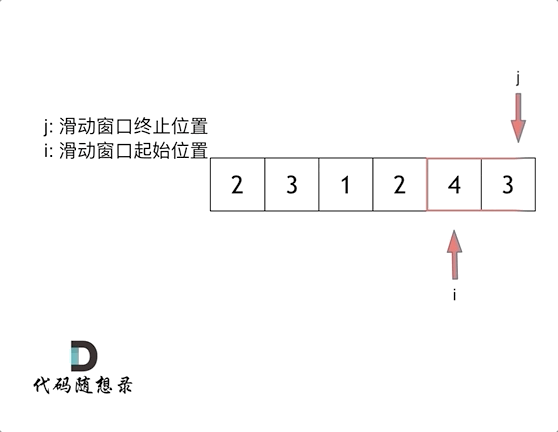
java
//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int left = 0, right = 0, sum = 0, minLen = Integer.MAX_VALUE;
while (right < nums.length) {
sum += nums[right];
while (sum >= target) {
minLen = Math.min(minLen, right - left + 1);
sum -= nums[left];
left++;
}
right++;
}
return minLen == Integer.MAX_VALUE ? 0 : minLen;
}
}
//leetcode submit region end(Prohibit modification and deletion)2 螺旋数组59
java
package com.jiangxun.leetcode.editor.cn;//<p>给你一个正整数 <code>n</code> ,生成一个包含 <code>1</code> 到 <code>n<sup>2</sup></code> 所有元素,且元素按顺时针顺序螺旋排列的 <code>n x n</code> 正方形矩阵 <code>matrix</code> 。</p>
//
//<p> </p>
//
//<p><strong>示例 1:</strong></p>
//<img alt="" src="https://assets.leetcode.com/uploads/2020/11/13/spiraln.jpg" style="width: 242px; height: 242px;" />
//<pre>
//<strong>输入:</strong>n = 3
//<strong>输出:</strong>[[1,2,3],[8,9,4],[7,6,5]]
//</pre>
//
//<p><strong>示例 2:</strong></p>
//
//<pre>
//<strong>输入:</strong>n = 1
//<strong>输出:</strong>[[1]]
//</pre>
//
//<p> </p>
//
//<p><strong>提示:</strong></p>
//
//<ul>
// <li><code>1 <= n <= 20</code></li>
//</ul>
//
//<div><div>Related Topics</div><div><li>数组</li><li>矩阵</li><li>模拟</li></div></div><br><div><li>👍 1340</li><li>👎 0</li></div>
//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
public int[][] generateMatrix(int n) {
int[][] nums = new int[n][n];
//从1开始放数字
int number = 1;
//循环次数count
int count = 1;
//起点(x,y),i是行,j是列
int startX = 0;
int startY = 0;
int i=1;
int j=1;
//初始化偏移值设为 1,固定某一循环,每一次填充数量
int offset = 1;
/**
* 3*3的矩阵
* 第一次填充上部 1 2,第二次填充右侧 3 4 左闭右开
* 第三次填充下部 5 6,第四次填充左部 7 8
* (以此循环)填充 9
*/
while (count <= n / 2) {
//上
for (j = startY; j < n - offset; j++) {
nums[i][j] = number++;
}
//右
for (i = startX; i < n - offset; i++) {
nums[i][j] = number++;
}
//下
for(; j > startY; j--){
nums[i][j] = number++;
}
//左
for(; i > startX; i--){
nums[i][j] = number++;
}
//更新起点
startX++;
startY++;
//更新偏移值
offset++;
//更新循环次数
count++;
}
//如果n是奇数,单独处理中间数字
if(n % 2 == 1){
nums[startX][startY] = number;
}
return nums;
}
}
//leetcode submit region end(Prohibit modification and deletion)
java
package com.jiangxun.leetcode.editor.cn;//<p>给你一个正整数 <code>n</code> ,生成一个包含 <code>1</code> 到 <code>n<sup>2</sup></code> 所有元素,且元素按顺时针顺序螺旋排列的 <code>n x n</code> 正方形矩阵 <code>matrix</code> 。</p>
//
//<p> </p>
//
//<p><strong>示例 1:</strong></p>
//<img alt="" src="https://assets.leetcode.com/uploads/2020/11/13/spiraln.jpg" style="width: 242px; height: 242px;" />
//<pre>
//<strong>输入:</strong>n = 3
//<strong>输出:</strong>[[1,2,3],[8,9,4],[7,6,5]]
//</pre>
//
//<p><strong>示例 2:</strong></p>
//
//<pre>
//<strong>输入:</strong>n = 1
//<strong>输出:</strong>[[1]]
//</pre>
//
//<p> </p>
//
//<p><strong>提示:</strong></p>
//
//<ul>
// <li><code>1 <= n <= 20</code></li>
//</ul>
//
//<div><div>Related Topics</div><div><li>数组</li><li>矩阵</li><li>模拟</li></div></div><br><div><li>👍 1340</li><li>👎 0</li></div>
//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
public int[][] generateMatrix(int n) {
int[][] nums = new int[n][n];
//从1开始放数字
int number = 1;
//循环次数count
int count = 1;
//起点(x,y),i是行,j是列
int startX = 0;
int startY = 0;
int i=1;
int j=1;
//初始化偏移值设为 1,固定某一循环,每一次填充数量
int offset = 1;
/**
* 3*3的矩阵
* 第一次填充上部 1 2,第二次填充右侧 3 4 左闭右开
* 第三次填充下部 5 6,第四次填充左部 7 8
* (以此循环)填充 9
*/
while (count <= n / 2) {
//上
for (j = startY; j < n - offset; j++) {
i=startX;
nums[i][j] = number++;
}
//右
for (i = startX; i < n - offset; i++) {
nums[i][j] = number++;
}
//下
for(; j > startY; j--){
nums[i][j] = number++;
}
//左
for(; i > startX; i--){
nums[i][j] = number++;
}
//更新起点
startX++;
startY++;
//更新偏移值
offset++;
//更新循环次数
count++;
}
//如果n是奇数,单独处理中间数字
if(n % 2 == 1){
nums[startX][startY] = number;
}
return nums;
}
}
//leetcode submit region end(Prohibit modification and deletion)- 区间和
【题目描述】
在一个城市区域内,被划分成了n * m个连续的区块,每个区块都拥有不同的权值,代表着其土地价值。目前,有两家开发公司,A 公司和 B 公司,希望购买这个城市区域的土地。
现在,需要将这个城市区域的所有区块分配给 A 公司和 B 公司。
然而,由于城市规划的限制,只允许将区域按横向或纵向划分成两个子区域,而且每个子区域都必须包含一个或多个区块。
为了确保公平竞争,你需要找到一种分配方式,使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。
注意:区块不可再分。
【输入描述】
第一行输入两个正整数,代表 n 和 m。
接下来的 n 行,每行输出 m 个正整数。
输出描述
请输出一个整数,代表两个子区域内土地总价值之间的最小差距。
【输入示例】
3 3 1 2 3 2 1 3 1 2 3
【输出示例】
0
【提示信息】
如果将区域按照如下方式划分:
1 2 | 3 2 1 | 3 1 2 | 3
两个子区域内土地总价值之间的最小差距可以达到 0。
【数据范围】:
1 <= n, m <= 100;
n 和 m 不同时为 1。
#思路
看到本题,大家如果想暴力求解,应该是 n^3 的时间复杂度,
一个 for 枚举分割线, 嵌套 两个for 去累加区间里的和。
如果本题要求 任何两个行(或者列)之间的数值总和,大家在0058.区间和 的基础上 应该知道怎么求。
就是前缀和的思路,先统计好,前n行的和 q[n],如果要求矩阵 a行 到 b行 之间的总和,那么就 q[b] - q[a - 1]就好。
至于为什么是 a - 1,大家去看 0058.区间和 的分析,使用 前缀和 要注意 区间左右边的开闭情况。
本题也可以使用 前缀和的思路来求解,先将 行方向,和 列方向的和求出来,这样可以方便知道 划分的两个区间的和。
java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int sum = 0;
int[][] vec = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
vec[i][j] = scanner.nextInt();
sum += vec[i][j];
}
}
// 统计横向
int[] horizontal = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
horizontal[i] += vec[i][j];
}
}
// 统计纵向
int[] vertical = new int[m];
for (int j = 0; j < m; j++) {
for (int i = 0; i < n; i++) {
vertical[j] += vec[i][j];
}
}
int result = Integer.MAX_VALUE;
int horizontalCut = 0;
for (int i = 0; i < n; i++) {
horizontalCut += horizontal[i];
result = Math.min(result, Math.abs(sum - 2 * horizontalCut));
}
int verticalCut = 0;
for (int j = 0; j < m; j++) {
verticalCut += vertical[j];
result = Math.min(result, Math.abs(sum - 2 * verticalCut));
}
System.out.println(result);
scanner.close();
}
}
day03 链表
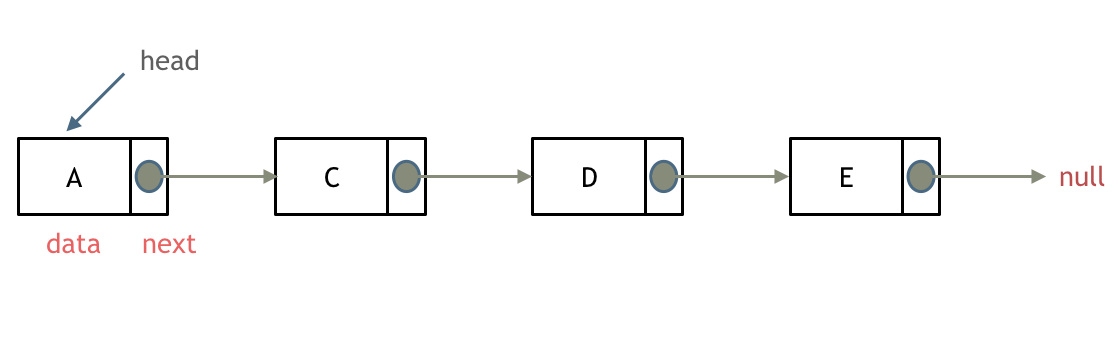
单链表:链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。链表的入口节点称为链表的头结点也就是head。
双链表
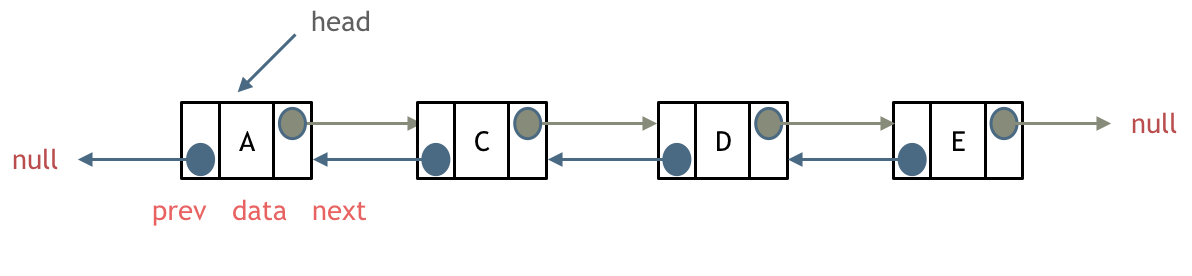
单链表中的指针域只能指向节点的下一个节点。
双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。
双链表 既可以向前查询也可以向后查询。
循环链表
循环链表,顾名思义,就是链表首尾相连。
循环链表可以用来解决约瑟夫环问题。
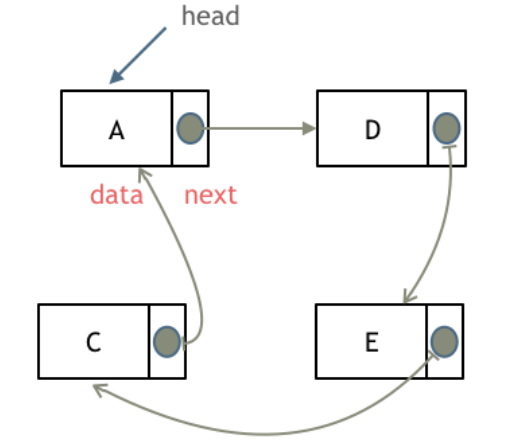
链表的存储方式
了解完链表的类型,再来说一说链表在内存中的存储方式。
数组是在内存中是连续分布的,但是链表在内存中可不是连续分布的。
链表是通过指针域的指针链接在内存中各个节点。
所以链表中的节点在内存中不是连续分布的 ,而是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理。
链表的定义
接下来说一说链表的定义。
链表节点的定义,很多同学在面试的时候都写不好。
这是因为平时在刷leetcode的时候,链表的节点都默认定义好了,直接用就行了,所以同学们都没有注意到链表的节点是如何定义的。
而在面试的时候,一旦要自己手写链表,就写的错漏百出。
这里我给出C/C++的定义链表节点方式
java
public static class ListNode{
// 节点上存储的元素
int val;
// 指向下一个节点的指针
ListNode next;
// 节点的构造函数
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
203 移除链表元素
plain
class Solution203 {
public ListNode removeElements(ListNode head, int val) {
ListNode dummyHead = new ListNode();
dummyHead.next = head;
ListNode cur = dummyHead;
while (cur.next != null) {
if (cur.next.val == val) {
cur.next = cur.next.next;
} else {
cur = cur.next;
}
}
return dummyHead.next;
}
/*
public ListNode removeElements(ListNode head, int val) {
while(head!=null&&head.val==val){
head=head.next;
}
ListNode cur=head;
while(cur!=null && cur.next!=null){
if(cur.next.val==val){
cur.next=cur.next.next;
}else {
cur=cur.next;
}
}
return head;
}
*/
}707 设计链表
plain
class ListNode {
int val;
ListNode next;
ListNode prev;
ListNode() {}
ListNode(int val) {
this.val = val;
}
ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
ListNode(int val, ListNode next, ListNode prev) { // 构造函数新增 prev 参数
this.val = val;
this.next = next;
this.prev = prev;
}
}
class MyLinkedList {
//记录链表中元素的数量
int size;
//记录链表的虚拟头结点和尾结点
ListNode head,tail;
public MyLinkedList() {
//初始化操作
this.size = 0;
this.head = new ListNode(0);
this.tail = new ListNode(0);
//这一步非常关键,否则在加入头结点的操作中会出现null.next的错误!!!
head.next=tail;
tail.prev=head;
}
public int get(int index) {
//判断index是否有效
if(index>=size){
return -1;
}
ListNode cur = this.head;
//判断是哪一边遍历时间更短
if(index >= size / 2){
//tail开始
cur = tail;
for(int i=0; i< size-index; i++){
cur = cur.prev;
}
}else{
for(int i=0; i<= index; i++){
cur = cur.next;
}
}
return cur.val;
}
public void addAtHead(int val) {
//等价于在第0个元素前添加
addAtIndex(0,val);
}
public void addAtTail(int val) {
//等价于在最后一个元素(null)前添加
addAtIndex(size,val);
}
public void addAtIndex(int index, int val) {
//index大于链表长度
if(index>size){
return;
}
size++;
//找到前驱
ListNode pre = this.head;
for(int i=0; i<index; i++){
pre = pre.next;
}
//新建结点
ListNode newNode = new ListNode(val);
newNode.next = pre.next;
pre.next.prev = newNode;
newNode.prev = pre;
pre.next = newNode;
}
public void deleteAtIndex(int index) {
//判断索引是否有效
if(index>=size){
return;
}
//删除操作
size--;
ListNode pre = this.head;
for(int i=0; i<index; i++){
pre = pre.next;
}
pre.next.next.prev = pre;
pre.next = pre.next.next;
}
}
/*
class MyLinkedList {
int size;
*/
/**
* 虚拟头节点
*//*
ListNode dummyHead;
*/
/**
* 初始化链表
*//*
public MyLinkedList() {
size = 0;
dummyHead = new ListNode();
}
public int get(int index) {
if (index < 0 || index >= size) {
return -1;
}
ListNode curNode = dummyHead;
//包含虚拟头节点,找index+1个节点
for (int i = 0; i < index + 1; i++) {
curNode = curNode.next;
}
return curNode.val;
}
public void addAtHead(int val) {
ListNode newNode=new ListNode(val);
//先处理后面一条线,在处理前面的线
newNode.next=dummyHead.next;
dummyHead.next=newNode;
size++;
}
public void addAtTail(int val) {
ListNode newNode=new ListNode(val);
//找到尾节点
ListNode cur=dummyHead;
while(cur.next!=null){
cur = cur.next;
}
cur.next=newNode;
size++;
}
*/
/**
* addAtIndex(0, int val) 头插
* addAtIndex(size, int val) 尾插
* index>size,返回-1
*//*
public void addAtIndex(int index, int val) {
if(index>size){
return;
}
if(index<0){
return;
}
//找到前驱节点
ListNode predNode=dummyHead;
for (int i=0;i<index;i++){
predNode=predNode.next;
}
//创建待插入的新结点
ListNode toAddNode=new ListNode(val);
//先处理后一根线,再处理前面一个线
toAddNode.next=predNode.next;
predNode.next=toAddNode;
//长度加一
size++;
}
public void deleteAtIndex(int index) {
if(index<0||index>=size){
return;
}
//有虚拟头节点,不用考虑index=0;
ListNode predNode=dummyHead;
//找到前驱接节点
for(int i=0;i<index;i++){
predNode=predNode.next;
}
predNode.next=predNode.next.next;
size--;
}
}
*/206 反转链表
plain
class Solution206 {
public ListNode reverseList(ListNode head){
//递归
return reverse(null,head);
}
private ListNode reverse(ListNode prev, ListNode cur) {
if(cur==null){
return prev;
}
ListNode temp=null;
temp=cur.next;
cur.next=prev;
return reverse(cur,temp);
}
/*public ListNode reverseList(ListNode head) {
//双指针
ListNode prevNode=null;
ListNode curNode=head;
ListNode tempNode=null;
while(curNode!=null){
tempNode=curNode.next;
curNode.next=prevNode;
prevNode=curNode;
curNode=tempNode;
}
return prevNode;
}*/
}
day04 链表
24 两两交换链表中的节点
java
public ListNode swapPairs(ListNode head) {
// base case 退出提交
if(head == null || head.next == null) return head;
// 获取当前节点的下一个节点
ListNode next = head.next;
// 进行递归
ListNode newNode = swapPairs(next.next);
// 这里进行交换
next.next = head;
head.next = newNode;
return next;
}19.删除链表的倒数第N个节点
java
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummyNode = new ListNode(0);
dummyNode.next = head;
ListNode fast = dummyNode;
ListNode slow = dummyNode;
// 快慢指针差n个节点
for (int i = 0; i <= n; i++) {
fast=fast.next;
}
while (fast!=null){
fast=fast.next;
slow=slow.next;
}
if(slow.next!=null){
slow.next=slow.next.next;
}
return dummyNode.next;
}面试题 02.07. 链表相交
java
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode p1 = headA, p2 = headB;
while (p1 != p2) {
if (p1 == null) p1 = headB;
else p1 = p1.next;
if (p2 == null) p2 = headA;
else p2 = p2.next;
}
return p1;
}
}- 环形链表 II
java
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
ListNode index1 = fast;
ListNode index2 = head;
while (index1 != index2) {
index1 = index1.next;
index2 = index2.next;
}
return index1;
}
}
return null;
}
}总结
- 链表理论基础
链表是一种线性数据结构,但不像数组那样在内存中连续存储。链表由一系列节点组成,每个节点包含数据部分和一个指向列表中下一个节点的引用(或指针)。 - 移除链表元素 (Remove Linked List Elements)
题目要求移除链表中所有具有特定值的元素。可以通过遍历链表并检查每个节点的数据来实现。如果节点的数据等于给定值,就跳过该节点,即让前一个节点直接指向下一个节点。 - 设计链表 (Design Linked List)
题目要求实现一个单链表类,支持一些基本操作如获取、添加、删除节点等。通常需要定义一个内部的节点类,并且维护一个指向链表头部的指针。 - 翻转链表 (Reverse Linked List)
翻转链表是一个常见的面试题,可以通过迭代或递归的方式来解决。迭代方法中,我们需要三个指针分别用来记录当前节点、前一个节点和后一个节点。 - 两两交换链表中的节点 (Swap Nodes in Pairs)
这个题目要求以两个节点为一组进行交换。可以使用递归或迭代的方法来解决,关键在于正确地调整节点之间的连接关系。 - 删除链表的倒数第N个节点 (Remove Nth Node From End of List)
为了删除链表的倒数第N个节点,可以使用双指针技术。首先让第一个指针向前移动N步,然后同时移动两个指针直到第一个指针到达链表末尾。此时第二个指针所指向的就是要删除的节点。 - 链表相交 (Intersection of Two Linked Lists)
要找到两个链表的交点,可以先计算两个链表的长度,然后让较长的链表先走几步,使两个链表剩余长度相同。之后同步遍历两个链表,当遇到相同的节点时即为交点。 - 环形链表II (Linked List Cycle II)
检测链表中是否存在环,并返回环的起始节点。这通常通过快慢指针法实现,先用快慢指针检测环的存在,再通过数学方法找到环的入口。
day06 哈希表
1 哈希表理论基础
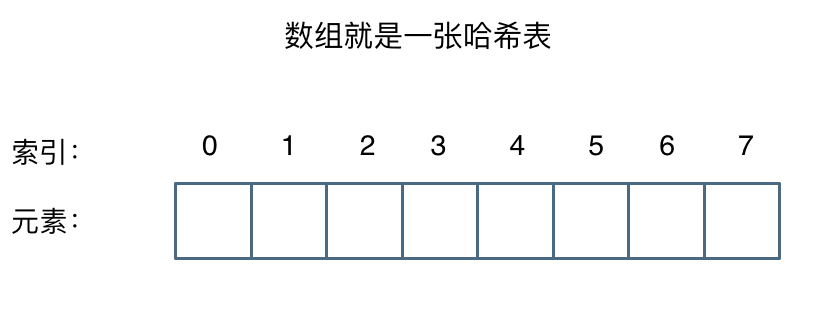
哈希函数,把学生的姓名直接映射为哈希表上的索引,然后就可以通过查询索引下标快速知道这位同学是否在这所学校里了。
哈希函数如下图所示,通过hashCode把名字转化为数值,一般hashcode是通过特定编码方式,可以将其他数据格式转化为不同的数值,这样就把学生名字映射为哈希表上的索引数字了。
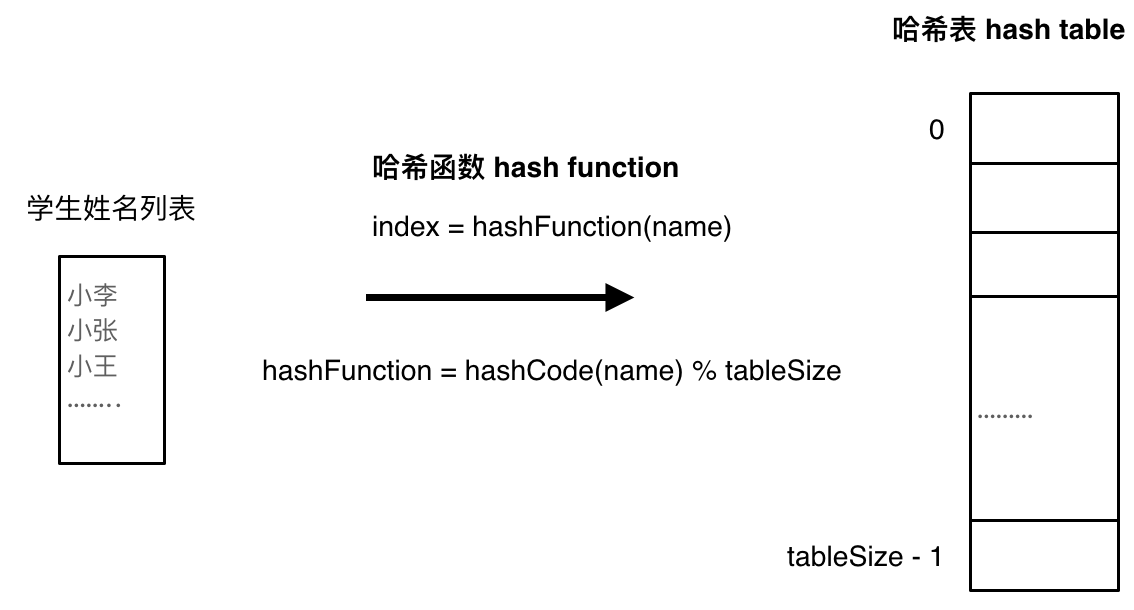
如果hashCode得到的数值大于 哈希表的大小了,也就是大于tableSize了,怎么办呢?
此时为了保证映射出来的索引数值都落在哈希表上,我们会在再次对数值做一个取模的操作,这样我们就保证了学生姓名一定可以映射到哈希表上了。
此时问题又来了,哈希表我们刚刚说过,就是一个数组。
如果学生的数量大于哈希表的大小怎么办,此时就算哈希函数计算的再均匀,也避免不了会有几位学生的名字同时映射到哈希表 同一个索引下标的位置。
接下来哈希碰撞登场
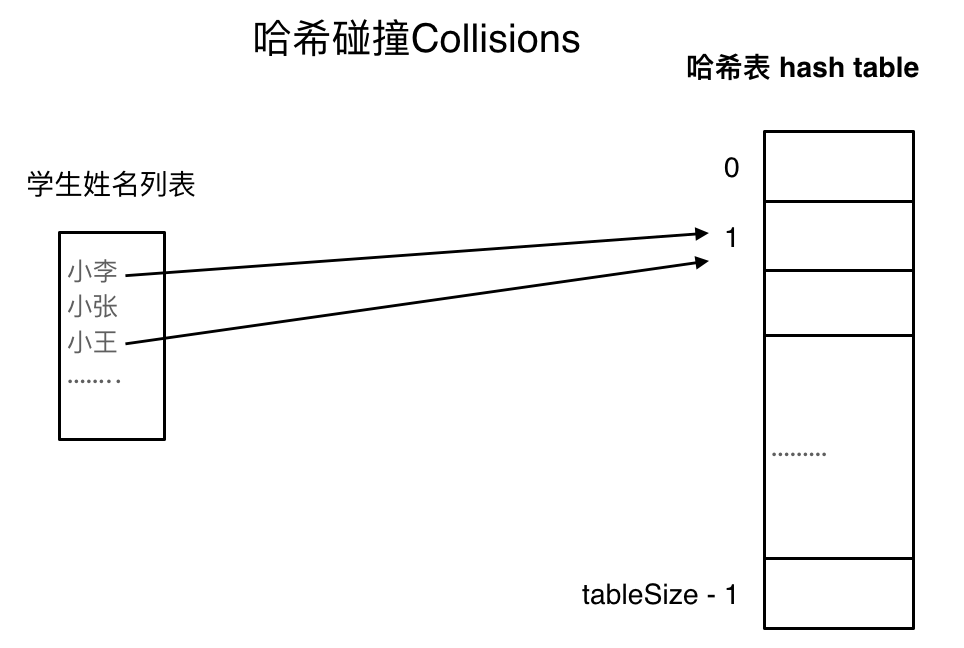
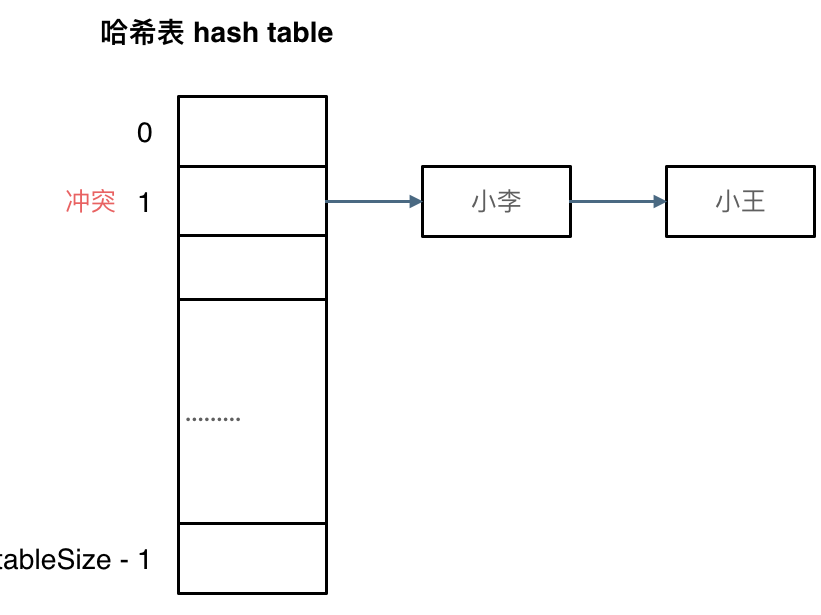
拉链法
(数据规模是dataSize, 哈希表的大小为tableSize)
其实拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
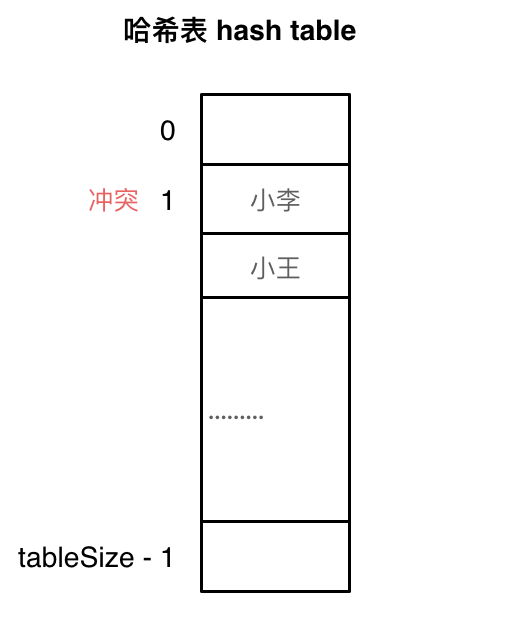
线性探测法
使用线性探测法,一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。
例如冲突的位置,放了小李,那么就向下找一个空位放置小王的信息。所以要求tableSize一定要大于dataSize ,要不然哈希表上就没有空置的位置来存放 冲突的数据了。
常见的三种哈希结构
当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。
- 数组
- set (集合)
- map(映射)
这里数组就没啥可说的了,我们来看一下set。
在C++中,set 和 map 分别提供以下三种数据结构,其底层实现以及优劣如下表所示:
| 集合 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::set | 红黑树 | 有序 | 否 | 否 | O(log n) | O(log n) |
| std::multiset | 红黑树 | 有序 | 是 | 否 | O(logn) | O(logn) |
| std::unordered_set | 哈希表 | 无序 | 否 | 否 | O(1) | O(1) |
std::unordered_set底层实现为哈希表,std::set 和std::multiset 的底层实现是红黑树,红黑树是一种平衡二叉搜索树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加。
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::map | 红黑树 | key有序 | key不可重复 | key不可修改 | O(logn) | O(logn) |
| std::multimap | 红黑树 | key有序 | key可重复 | key不可修改 | O(log n) | O(log n) |
| std::unordered_map | 哈希表 | key无序 | key不可重复 | key不可修改 | O(1) | O(1) |
242.有效的字母异位词
java
class Solution {
public boolean isAnagram(String s, String t) {
int[] record=new int[26];
for(int i=0;i<s.length();i++){
record[s.charAt(i)-'a']++;
}
for(int i=0;i<t.length();i++){
record[t.charAt(i)-'a']--;
}
for(int count:record){
if(count!=0){
return false;
}
}
return true;
}
}- 两个数组的交集
java
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
int[] hash1 = new int[1002];
int[] hash2 = new int[1002];
for(int i : nums1)
hash1[i]++;
for(int i : nums2)
hash2[i]++;
List<Integer> resList = new ArrayList<>();
for(int i = 0; i < 1002; i++)
if(hash1[i] > 0 && hash2[i] > 0)
resList.add(i);
int index = 0;
int res[] = new int[resList.size()];
for(int i : resList)
res[index++] = i;
return res;
}
}- 快乐数
java
class Solution {
public boolean isHappy(int n) {
Set<Integer> record = new HashSet<>();
while (n != 1 && !record.contains(n)) {
record.add(n);
n = getNextNumber(n);
}
return n == 1;
}
private int getNextNumber(int n) {
int res = 0;
while (n > 0) {
int temp = n % 10;
res += temp * temp;
n = n / 10;
}
return res;
}
}- 两数之和
java
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> indexMap = new HashMap<>();
for(int i = 0; i < nums.length; i++){
int balance = target - nums[i]; // 记录当前的目标值的余数
if(indexMap.containsKey(balance)){ // 查找当前的map中是否有满足要求的值
return new int []{i, indexMap.get(balance)}; // 如果有,返回目标值
} else{
indexMap.put(nums[i], i); // 如果没有,把访问过的元素和下标加入map中
}
}
return null;
}
}