1. 简单介绍
我们知道set和map的底层为红黑树,使用迭代器进行遍历时(中序),所得到的数据是有序的。
而unordered_set和unordered_map的底层为哈希表,顾名思义,二者存储的数据是无序的。
虽然数据无序,但unordered_set和unordered_map的查找效率可达O(1),在一些只要求能快速查找而不要求有序场景下有很高的价值,因此也在C++11中被纳入了标准。
unordered_set/unordered_map与set/map的使用如出一辙,只是一个数据有序,一个数据无序。
所以在这里我们就不多介绍其用法了,大家可以参考set/map的使用方法:
或者直接参考文档:
2. 模拟实现
unordered太难写了,接下来都直接简称set/map。
2.1 set/map专用哈希表
仅用于学习原理的哈希表我们已经实现过了:
要用来适配出unordered_set和unoerdered_map还需要对其进行一些修改,我们使用链地址法的那一版来进行修改。
首先我们要明确,set/map的最主要的区别只在于存储的是key还是pair,底层的哈希表逻辑基本相同,所以我们修改出来的哈希表最好能同时适配出二者。
所以如何区别存储的数据是key还是pair呢?因为在查找删除时用到的都是key,如果存储的是pair,我们还需要访问pair的first才能得到key。
2.1.1 仿函数KeyOfT
参照STL源码,我们可以看到其解决上面问题的方式是:
在哈希表的参数列表中传入仿函数KeyOfT,用于获取数据(T)的key,该仿函数在set和map的中分别实现并传给自身内部的哈希表。
对于set来说,SetKeyOfT直接返回数据本身;对于map来说,MapKeyOfT返回pair的first。
cpp
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
struct MapKeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};这样,在哈希表内部需要用到key时,统一使用仿函数KeyOfT取得,就不需要对二者进行区分了。
相应地,我们要对数据结点进行修改:
cpp
template<class T>
struct HashNode
{
T _data;
HashNode* _next;
HashNode(const T& data)
:_data(data)
, _next(nullptr)
{}
};在哈希表地参数列表中,也不以传入K,V的方式传入数据类型了,而是传入K,T:
cpp
template<class K, class T, class KeyOfT, class Hash, class Compare>
class HashTable另外,Hash和Compare也由外层的set/map指定,所以也不需要缺省值了。
注意,这样修改之后,各个函数都需要相应地发生变化,注意修改。
2.1.2 迭代器
unordered_set/unordered_map的迭代器是单向迭代器,底层就是对结点指针的包装。
迭代器实现中唯一的难点就是,当一个桶中没有任何数据或访问到桶的最后一个数据时,需要跳转到下一个有数据的桶中,也就是operator++的逻辑。
如果能访问到哈希表内部的数组,这一点自然很好解决。
而为了降低耦合提高代码的可维护性,迭代器与哈希表是分开实现的,且哈希表内部的数组是private成员。
参考STL源代码,其解决方式是给迭代器增加一个指向对应哈希表的指针成员,并声明为哈希表的友元类,以便其访问哈希表底层的数组。
cpp
// 前置声明
template<class K, class T, class KeyOfT, class Hash, class Compare>
class HashTable;
template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash, class Compare>
class HTIterator
{
typedef HashNode<T> Node;
typedef HTIterator<K, T, Ref, Ptr, KeyOfT, Hash, Compare> Self;
typedef HashTable<K, T, KeyOfT, Hash, Compare> Table;
public:
HTIterator(Node* node, Table* pHT)
:_node(node)
, _pHT(pHT)
{}
template<class reference, class pointer>
HTIterator(const HTIterator<K, T, reference, pointer, KeyOfT, Hash, Compare>& it)
:_node(it._node)
, _pHT(it._pHT)
{}
bool operator==(const Self& it)
{
return _node == it._node;
}
bool operator!=(const Self& it)
{
return _node != it._node;
}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &(_node->_data);
}
Self& operator++()
{
assert(_node);
if (_node->_next)
_node = _node->_next;
else
{
size_t pos = _hash(_keyOf(_node->_data)) % _pHT->_tables.size();
++pos;
while (pos < _pHT->_tables.size() && _pHT->_tables[pos] == nullptr)
{
++pos;
}
if (pos < _pHT->_tables.size())
_node = _pHT->_tables[pos];
else
_node = nullptr;
}
return *this;
}
Self operator++(int)
{
Self it = *this;
++(*this);
return it;
}
private:
Node* _node;
Table* _pHT;
Hash _hash;
KeyOfT _keyOf;
};注意,模板声明为友元类需要带上参数列表:
cpp
template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash, class Compare>
friend class HTIterator;2.1.3 插入函数
由于map需要实现operator[],所以插入函数的返回值需要改为:
cpp
pair<iterator, bool>相应的逻辑也要发生变化:
cpp
pair<iterator, bool> Insert(const T& data)
{
iterator it = Find(_keyof(data));
if (it != end())
return {it, false};
// 负载因子等于1,扩容
if (_n == _tables.size())
{
vector<Node*> newTables(__stl_next_prime(_n + 1));
// 原结点依次插入新表
for (size_t i = 0; i < _n; i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t pos = _hash(_keyof(cur->_data)) % _tables.size();
cur->_next = newTables[pos];
newTables[pos] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newTables);
}
size_t pos = _hash(_keyof(data)) % _tables.size();
Node* newnode = new Node(data);
newnode->_next = _tables[pos];
_tables[pos] = newnode;
++_n;
return { iterator(newnode, this) , true};
}2.1.4 代码参考示例
cpp
#pragma once
#include<string>
#include<vector>
#include<assert.h>
using namespace std;
static const int __stl_num_primes = 28;
static const unsigned long __stl_prime_list[__stl_num_primes] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
inline unsigned long __stl_next_prime(unsigned long n)
{
const unsigned long* first = __stl_prime_list;
const unsigned long* last = __stl_prime_list + __stl_num_primes;
const unsigned long* pos = lower_bound(first, last, n);
return pos == last ? *(last - 1) : *pos;
}
// 哈希函数采用除留余数法
template<class K>
struct HashFunc
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
// 哈希表中支持字符串的操作
template<>
struct HashFunc<string>
{
size_t operator()(const string& key)
{
size_t hash = 0;
for (auto e : key)
{
hash *= 131;
hash += e;
}
return hash;
}
};
template<class K>
struct Equal
{
bool operator()(const K& key1, const K& key2)
{
return key1 == key2;
}
};
// 给unorder_set和unordered_map使用的HashTable
namespace lbz
{
template<class T>
struct HashNode
{
T _data;
HashNode* _next;
HashNode(const T& data)
:_data(data)
, _next(nullptr)
{}
};
// 前置声明
template<class K, class T, class KeyOfT, class Hash, class Compare>
class HashTable;
template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash, class Compare>
class HTIterator
{
typedef HashNode<T> Node;
typedef HTIterator<K, T, Ref, Ptr, KeyOfT, Hash, Compare> Self;
typedef HashTable<K, T, KeyOfT, Hash, Compare> Table;
public:
HTIterator(Node* node, Table* pHT)
:_node(node)
, _pHT(pHT)
{}
template<class reference, class pointer>
HTIterator(const HTIterator<K, T, reference, pointer, KeyOfT, Hash, Compare>& it)
:_node(it._node)
, _pHT(it._pHT)
{}
bool operator==(const Self& it)
{
return _node == it._node;
}
bool operator!=(const Self& it)
{
return _node != it._node;
}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &(_node->_data);
}
Self& operator++()
{
assert(_node);
if (_node->_next)
_node = _node->_next;
else
{
size_t pos = _hash(_keyOf(_node->_data)) % _pHT->_tables.size();
++pos;
while (pos < _pHT->_tables.size() && _pHT->_tables[pos] == nullptr)
{
++pos;
}
if (pos < _pHT->_tables.size())
_node = _pHT->_tables[pos];
else
_node = nullptr;
}
return *this;
}
Self operator++(int)
{
Self it = *this;
++(*this);
return it;
}
private:
Node* _node;
Table* _pHT;
Hash _hash;
KeyOfT _keyOf;
};
template<class K, class T, class KeyOfT, class Hash, class Compare>
class HashTable
{
template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash, class Compare>
friend class HTIterator;
typedef HashNode<T> Node;
typedef HashTable<K, T, KeyOfT, Hash, Compare> Self;
public:
typedef HTIterator<K, T, T&, T*, KeyOfT, Hash, Compare> iterator;
typedef HTIterator<K, T, const T&, const T*, KeyOfT, Hash, Compare> const_iterator;
HashTable()
:_tables(__stl_next_prime(0))
, _n(0)
{}
HashTable(const Self& hashtable)
:HashTable()
{
for (auto cur : hashtable._tables)
{
while (cur)
{
Insert(cur->_kv);
cur = cur->_next;
}
}
}
Self& operator=(Self hashtable)
{
swap(_tables, hashtable._tables);
swap(_n, hashtable._n);
return *this;
}
~HashTable()
{
for (auto cur : _tables)
{
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
}
}
iterator begin()
{
if (_n == 0)
return end();
size_t i = 0;
for (i = 0; i < _tables.size(); i++)
{
if (_tables[i] != nullptr)
break;
}
return iterator(_tables[i], this);
}
iterator end()
{
return iterator(nullptr, this);
}
const_iterator begin() const
{
if (_n == 0)
return end();
size_t i = 0;
for (i = 0; i < _tables.size(); i++)
{
if (_tables[i] != nullptr)
break;
}
return const_iterator(_tables[i], this);
}
const_iterator end() const
{
return const_iterator(nullptr, this);
}
pair<iterator, bool> Insert(const T& data)
{
iterator it = Find(_keyof(data));
if (it != end())
return {it, false};
// 负载因子等于1,扩容
if (_n == _tables.size())
{
vector<Node*> newTables(__stl_next_prime(_n + 1));
// 原结点依次插入新表
for (size_t i = 0; i < _n; i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t pos = _hash(_keyof(cur->_data)) % _tables.size();
cur->_next = newTables[pos];
newTables[pos] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newTables);
}
size_t pos = _hash(_keyof(data)) % _tables.size();
Node* newnode = new Node(data);
newnode->_next = _tables[pos];
_tables[pos] = newnode;
++_n;
return { iterator(newnode, this) , true};
}
iterator Find(const K& key)
{
size_t pos = _hash(key) % _tables.size();
Node* cur = _tables[pos];
while (cur && !_com(_keyof(cur->_data), key)) { cur = cur->_next; }
return iterator(cur, this);
}
bool Erase(const K& key)
{
size_t pos = _hash(key) % _tables.size();
if (_tables[pos] == nullptr)
return false;
Node* del = nullptr;
if (_com(_keyof(_tables[pos]->_data), key))
{
del = _tables[pos];
_tables[pos] = _tables[pos]->_next;
}
else
{
Node* parent = _tables[pos];
while (parent->_next && !_com(_keyof(parent->_next->_data), key))
{
parent = parent->_next;
}
if (parent->_next == nullptr)
return false;
del = parent->_next;
parent->_next = parent->_next->_next;
}
delete del;
--_n;
return true;
}
private:
vector<Node*> _tables;
size_t _n = 0; // 表中存储数据个数
Hash _hash;
Compare _com;
KeyOfT _keyof;
};
}2.2 unordered_set
没什么好说的,注意set中的key是不可修改的,所以在传入参数T时直接传入const K。
cpp
#pragma once
#include"hashTable.h"
namespace lbz
{
template<class K, class Hash = HashFunc<K>, class Compare = Equal<K>>
class unordered_set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename HashTable<K, const K, SetKeyOfT, Hash, Compare>::iterator iterator;
typedef typename HashTable<K, const K, SetKeyOfT, Hash, Compare>::const_iterator const_iterator;
pair<iterator, bool> Insert(const K& key)
{
return _hashtable.Insert(key);
}
bool Erase(const K& key)
{
return _hashtable.Erase(key);
}
iterator begin()
{
return _hashtable.begin();
}
iterator end()
{
return _hashtable.end();
}
const_iterator begin() const
{
return _hashtable.begin();
}
const_iterator end() const
{
return _hashtable.end();
}
private:
HashTable<K, const K, SetKeyOfT, Hash, Compare> _hashtable;
};
}2.3 unordered_map
也没什么好说的,就是还需要实现一个operator[],具体实现方式参考下面的代码(当然下面的代码也是参考STL源码实现的)。
cpp
#pragma once
#include"hashTable.h"
namespace lbz
{
template<class K, class V, class Hash = HashFunc<K>, class Compare = Equal<K>>
class unordered_map
{
struct MapKeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename HashTable<K, pair<const K, V>, MapKeyOfT, Hash, Compare>::iterator iterator;
typedef typename HashTable<K, pair<const K, V>, MapKeyOfT, Hash, Compare>::const_iterator const_iterator;
pair<iterator, bool> Insert(const pair<K, V>& kv)
{
return _hashtable.Insert(kv);
}
bool Erase(const K& key)
{
return _hashtable.Erase(key);
}
iterator begin()
{
return _hashtable.begin();
}
iterator end()
{
return _hashtable.end();
}
const_iterator begin() const
{
return _hashtable.begin();
}
const_iterator end() const
{
return _hashtable.end();
}
V& operator[](const K& key)
{
pair<iterator, bool> pr = _hashtable.Insert({ key, V() });
return pr.first->second;
}
private:
HashTable<K, pair<const K, V>, MapKeyOfT, Hash, Compare> _hashtable;
};
}3. 总结
unordered_set/unordered_map底层为哈希表,相比于底层为红黑树的set/map来说,数据无序但查找插入都更高效。
要自己实现unordered_set/unordered_map,重点在于底层哈希表的实现,难点在于各个结构之间的相互嵌套,参数类型的传值,在自己实现的过程中一定会出现很多问题的。而且报出来的错误会让你觉得牛头不对马嘴,例如:
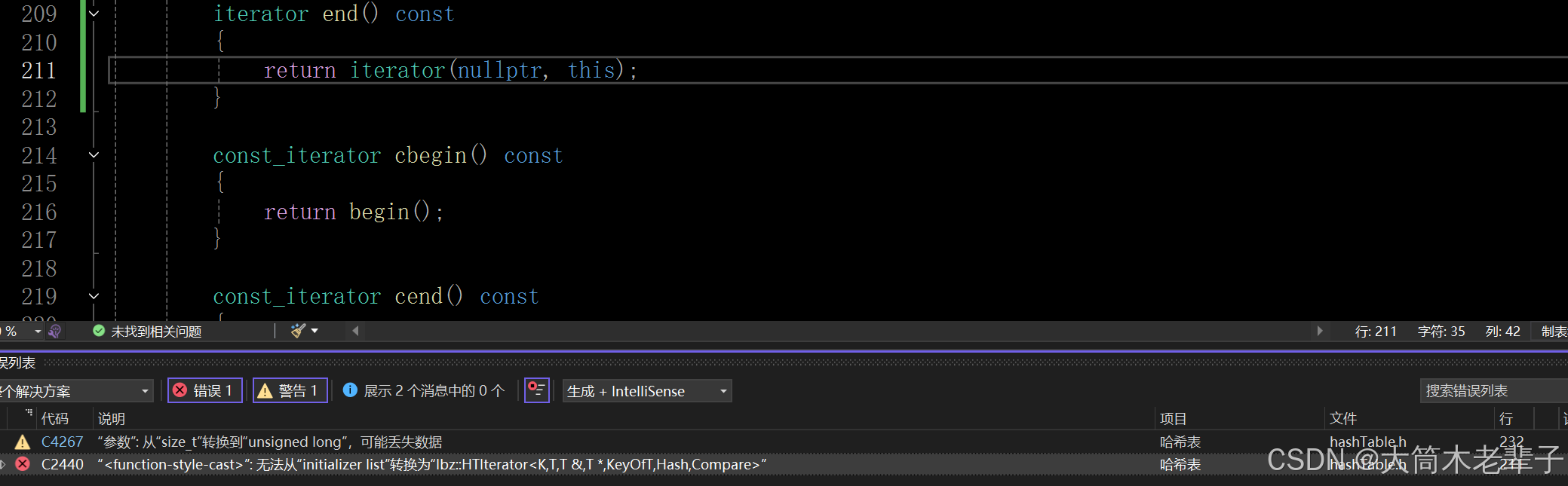
这是由于end()后面加上了const而发生的报错,但感觉怎么想二者之间都没关系,真给我搞红温了。
4. set/map的模拟实现
红黑树的实现可以参考:C++笔记---红黑树的插入删除_红黑树 删除-CSDN博客 。
这里我就不再多说了,基本实现思路与上面相似,但红黑树结构更复杂,在改的过程中会更加困难,有多难呢?难得我都不想再水一篇文章了,直接贴到下面大家参考一下吧。
4.1 SM_RBTree
就是set/map专用红黑树的意思,没什么含义哈。
cpp
#pragma once
#include"reverse_iterator.h"
namespace lbz
{
// 枚举值表示颜色
enum Colour
{
RED,
BLACK
};
// 这里我们默认按key/value结构实现
template<class T>
struct RBTreeNode
{
// 这里更新控制平衡也要加入parent指针
T _data;
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
Colour _col;
RBTreeNode(const T& data, Colour col = RED)
:_data(data)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _col(col)
{}
};
template<class T, class Ref, class Ptr>
struct RBTreeIterator
{
typedef RBTreeIterator<T, Ref, Ptr> Self;
typedef RBTreeNode<T> Node;
typedef T value_type;
typedef Ref reference;
typedef Ptr pointer;
public:
RBTreeIterator(Node* node = nullptr, Node* root = nullptr)
:_node(node)
,_root(root)
{}
RBTreeIterator(const Self& it)
:_node(it._node)
,_root(it._root)
{}
template<class T, class reference, class pointer>
RBTreeIterator(const RBTreeIterator<T, reference, pointer>& it)
:_node(it._node)
,_root(it._root)
{}
bool operator==(const Self& it) const
{
return _node == it._node;
}
bool operator!=(const Self& it) const
{
return _node != it._node;
}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &(_node->_data);
}
Self& operator++()
{
Node* next = nullptr;
if (_node->_right)
{
next = _node->_right;
while (next->_left) { next = next->_left; }
}
else
{
next = _node;
while (next->_parent && next == next->_parent->_right) { next = next->_parent; }
next = next->_parent;
}
_node = next;
return *this;
}
Self operator++(int)
{
Self tmp = *this;
++(*this);
return tmp;
}
Self& operator--()
{
Node* next = nullptr;
if (_node == nullptr)
{
next = _root;
while (next->_right) { next = next->_right; }
}
else if (_node->_left)
{
next = _node->_left;
while (next->_right) { next = next->_right; }
}
else
{
next = _node;
while (next->_parent && next == next->_parent->_left) { next = next->_parent; }
next = next->_parent;
}
_node = next;
return *this;
}
Self operator--(int)
{
Self tmp = *this;
--(*this);
return tmp;
}
Node* _node;
Node* _root;
};
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
typedef RBTree<K, T, KeyOfT> Self;
public:
typedef RBTreeIterator<T, T&, T*> iterator;
typedef RBTreeIterator<T, const T&, const T*> const_iterator;
typedef Reverse_iterator<iterator> reverse_iterator;
typedef Reverse_iterator<const_iterator> const_reverse_iterator;
public:
RBTree() = default;
RBTree(const RBTree& tree)
{
_root = Construct(tree._root);
}
RBTree(const initializer_list<const T>& li)
{
for (auto& e : li)
{
Insert(e);
}
}
~RBTree()
{
Destroy(_root);
_root = nullptr;
}
RBTree& operator=(RBTree tree)
{
std::swap(_root, tree._root);
return *this;
}
iterator begin()
{
Node* first = _root;
while (first->_left) { first = first->_left; }
return iterator(first, _root);
}
const_iterator begin() const
{
return (Self)(*this).begin();
}
iterator end()
{
return iterator(nullptr, _root);
}
const_iterator end() const
{
return (Self)(*this).end();
}
reverse_iterator rbegin()
{
return end();
}
const_reverse_iterator rbegin() const
{
return end();
}
reverse_iterator rend()
{
return begin();
}
const_reverse_iterator rend() const
{
return begin();
}
pair<iterator, bool> Insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return {iterator(_root, _root), true};
}
Node* cur = _root, * parent = nullptr;
while (cur)
{
parent = cur;
if (keyOf(data) < keyOf(cur->_data))
cur = cur->_left;
else if (keyOf(data) > keyOf(cur->_data))
cur = cur->_right;
else
return {iterator(cur, _root), false};
}
cur = new Node(data);
Node* ret = cur;
cur->_col = RED;
if (keyOf(data) < keyOf(cur->_data))
parent->_left = cur;
else
parent->_right = cur;
cur->_parent = parent;
while (parent && parent->_col == RED)
{
// 因为_root为黑色,所以parent为红色,grandfather一定存在且为黑色
Node* grandfather = parent->_parent;
// 不进行双旋时需变色
parent->_col = BLACK;
grandfather->_col = RED;
if (parent == grandfather->_left)// uncle在右子树
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)// uncle存在且为红,直接变色
{
uncle->_col = BLACK;
cur = grandfather;
parent = cur->_parent;
}
else// uncle不存在或为黑,变色加旋转
{
if (cur == parent->_right)
{
RotateL(parent);
if (uncle)
uncle->_col = RED;
parent->_col = RED;
cur->_col = BLACK;
}
RotateR(grandfather);
break;// 转后parent为子树根(黑),无需继续向上更新
}
}
else
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
uncle->_col = BLACK;
cur = grandfather;
parent = cur->_parent;
}
else
{
if (cur == parent->_left)
{
RotateR(parent);
if (uncle)
uncle->_col = RED;
parent->_col = RED;
cur->_col = BLACK;
}
RotateL(grandfather);
break;
}
}
}
_root->_col = BLACK;
return {iterator(ret, _root), true};
}
bool Erase(const K& k)
{
Node* del = Find(k);
if (del == nullptr)
return false;
// 两个孩子都有,更新要删除的结点
if (del->_left && del->_right)
{
Node* replace = del->_right;
while (replace->_left) { replace = replace->_left; }
std::swap(del->_data, replace->_data);
del = replace;
}
// 接下来处理至少一个孩子为空
if (del == _root)
_root = nullptr;
else if (del->_left || del->_right || del->_col == RED)// 有一个孩子或为红色
{
Node* child = del->_left ? del->_left : del->_right;
if (child)
child->_parent = del->_parent;
if (del->_parent->_left == del)
del->_parent->_left = child;
else
del->_parent->_right = child;
if (del->_col == BLACK)
child->_col = BLACK;
}
else// 没有孩子且为黑色
{
Node* cur = del;// 可能会向上调整,用cur代替del,始终认为cur无孩子
while (1)
{
if (cur->_parent->_col == RED)// 父结点为红色,一定有黑色兄弟,直接删除+变色
{
cur->_parent->_col = BLACK;
if (cur->_parent->_left == cur)
{
cur->_parent->_left = nullptr;
cur->_parent->_right->_col = RED;
}
else
{
cur->_parent->_right = nullptr;
cur->_parent->_left->_col = RED;
}
}
else// 父结点为黑色,看情况单双旋或调整
{
Node* parent = cur->_parent;
if (parent->_left == cur)// 在左,右边是兄弟
{
Node* brother = parent->_right;
parent->_left = nullptr;
if (brother->_col == RED)// 红色兄弟,一定有两个黑孩子
{
brother->_col = BLACK;
brother->_left->_col = RED;
RotateL(parent);
}
else// 黑色兄弟,要么没孩子,要么有红孩子
{
if (brother->_left == nullptr && brother->_right == nullptr)// 兄弟没孩子,差一个调不了,向上调整
{
brother->_col = RED;
cur = parent;
continue;
}
else if (brother->_right)
{
brother->_right->_col = BLACK;
RotateL(parent);
}
else
{
brother->_left->_col = BLACK;
RotateR(brother);
RotateL(parent);
}
}
}
else// 在右,左边是兄弟
{
Node* brother = parent->_left;
parent->_right = nullptr;
if (brother->_col == RED)// 红色兄弟,一定有两个黑孩子
{
brother->_col = BLACK;
brother->_right->_col = RED;
RotateR(parent);
}
else// 黑色兄弟,要么没孩子,要么有红孩子
{
if (brother->_left == nullptr && brother->_right == nullptr)// 兄弟没孩子,差一个调不了,向上调整
{
brother->_col = RED;
cur = parent;
continue;
}
else if (brother->_left)
{
brother->_left->_col = BLACK;
RotateR(parent);
}
else
{
brother->_right->_col = BLACK;
RotateL(brother);
RotateR(parent);
}
}
}
}
break;
}
}
delete del;
return true;
}
void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* subR = cur->_right;
parent->_left = subR;
if (subR)
subR->_parent = parent;
cur->_right = parent;
cur->_parent = parent->_parent;
if (parent->_parent)
{
if (parent->_parent->_left == parent)
parent->_parent->_left = cur;
else
parent->_parent->_right = cur;
}
parent->_parent = cur;
if (parent == _root)
_root = cur;
}
void RotateL(Node* parent)
{
Node* cur = parent->_right;
Node* subL = cur->_left;
parent->_right = subL;
if (subL)
subL->_parent = parent;
cur->_left = parent;
cur->_parent = parent->_parent;
if (parent->_parent)
{
if (parent->_parent->_left == parent)
parent->_parent->_left = cur;
else
parent->_parent->_right = cur;
}
parent->_parent = cur;
if (parent == _root)
_root = cur;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key < keyOf(cur->_data))
cur = cur->_left;
else if (key > keyOf(cur->_data))
cur = cur->_right;
else
return cur;
}
return nullptr;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool isRBTree()
{
if (_isRBTree(_root) == -1)
return false;
else
return true;
}
private:
Node* Construct(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copy = new Node(root->_data, root->_col);
copy->_left = Construct(root->_left);
copy->_left->_parent = copy;
copy->_right = Construct(root->_right);
copy->_right->_parent = copy;
return copy;
}
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << keyOf(_root->_data) << " ";
_InOrder(root->_right);
}
int _isRBTree(Node* root)
{
int flag = 0;
if (root == nullptr)
return 0;
if (root->_col == RED && root->_parent->_col == RED)
return -1;
if (root->_col == BLACK)
flag = 1;
int left = _isRBTree(root->_left);
int right = _isRBTree(root->_right);
if (left == right)
return left + flag;
else
return -1;
}
KeyOfT keyOf;
private:
Node* _root = nullptr;
};
}4.2 mySet
cpp
#pragma once
#include"SM_RBTree.h"
namespace lbz
{
template<class K>
class set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef RBTreeNode<K> Node;
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;
typedef typename RBTree<K, K, SetKeyOfT>::const_reverse_iterator reverse_iterator;
typedef typename RBTree<K, K, SetKeyOfT>::const_reverse_iterator const_reverse_iterator;
pair<iterator, bool> Insert(const K& key)
{
return _tree.Insert(key);
}
bool Erase(const K& key)
{
return _tree.Erase(key);
}
iterator begin()
{
return _tree.begin();
}
const_iterator begin() const
{
return _tree.begin();
}
iterator end()
{
return _tree.end();
}
const_iterator end() const
{
return _tree.end();
}
reverse_iterator rbegin()
{
return _tree.rbegin();
}
const_reverse_iterator rbegin() const
{
return _tree.rbegin();
}
reverse_iterator rend()
{
return _tree.rend();
}
const_reverse_iterator rend() const
{
return _tree.rend();
}
private:
RBTree<K, K, SetKeyOfT> _tree;
};
}4.3 myMap
cpp
#pragma once
#include"SM_RBTree.h"
namespace lbz
{
template<class K, class V>
class map
{
struct MapKeyOfT
{
const K& operator()(const pair<const K, V>& p)
{
return p.first;
}
};
public:
typedef pair<const K, V> T;
typedef RBTreeNode<T> Node;
typedef typename RBTree<K, T, MapKeyOfT>::iterator iterator;
typedef typename RBTree<K, T, MapKeyOfT>::const_iterator const_iterator;
typedef typename RBTree<K, T, MapKeyOfT>::reverse_iterator reverse_iterator;
typedef typename RBTree<K, T, MapKeyOfT>::const_reverse_iterator const_reverse_iterator;
pair<iterator, bool> Insert(const T& data)
{
return _tree.Insert(data);
}
bool Erase(const T& data)
{
return _tree.Erase(data);
}
V& operator[](const K& key)
{
pair<iterator, bool> p = Insert({ key, V() });
return p.first->second;
}
iterator begin()
{
return _tree.begin();
}
const_iterator begin() const
{
return _tree.begin();
}
iterator end()
{
return _tree.end();
}
const_iterator end() const
{
return _tree.end();
}
reverse_iterator rbegin()
{
return _tree.rbegin();
}
const_reverse_iterator rbegin() const
{
return _tree.rbegin();
}
reverse_iterator rend()
{
return _tree.rend();
}
const_reverse_iterator rend() const
{
return _tree.rend();
}
private:
RBTree<K, pair<const K, V>, MapKeyOfT> _tree;
};
}