Exercise 2.63
Each of the following two procedures converts a binary tree to a list.
(define (tree->list-1 tree)
(if (null? tree)
'()
(append (tree->list-1 (left-branch tree))
(cons (entry tree)
(tree->list-1
(right-branch tree))))))
(define (tree->list-2 tree)
(define (copy-to-list tree result-list)
(if (null? tree)
result-list
(copy-to-list (left-branch tree)
(cons (entry tree)
(copy-to-list
(right-branch tree)
result-list)))))
(copy-to-list tree '()))a. Do the two procedures produce the same result for every tree? If not, how do the results differ? What lists do the two procedures produce for the trees in Figure 2.16?
b. Do the two procedures have the same order of growth in the number of steps required to convert a balanced tree withn elements to a list? If not, which one grows more slowly?
a. 对于 图2.16 的三种形式,这两个函数执行的结果是相同的,如下所示:
(define t1 (make-tree 3 (make-tree 1 '() '()) (make-tree 5 '() '())))
(define t2 (make-tree 9 '() (make-tree 11 '() '())))
(define test1 (make-tree 7 t1 t2))
(tree->list-1 test1)
(tree->list-2 test1)
(define t3 (make-tree 3 (make-tree 1 '() '()) '()))
(define t4 (make-tree 9 (make-tree 7 '() '()) (make-tree 11 '() '())))
(define test2 (make-tree 5 t3 t4))
(tree->list-1 test2)
(tree->list-2 test2)
(define t5 (make-tree 1 '() '()))
(define t6 (make-tree 7 (make-tree 5 '() '()) (make-tree 9 '() (make-tree 11 '() '()))))
(define test3 (make-tree 3 t5 t6))
(tree->list-1 test3)
(tree->list-2 test3)
; 结果如下
'(1 3 5 7 9 11)
'(1 3 5 7 9 11)
'(1 3 5 7 9 11)
'(1 3 5 7 9 11)
'(1 3 5 7 9 11)
'(1 3 5 7 9 11)b. 对于 tree->list-1,因为 append 需要花费线性时间,所以T(n) = 2 * T(n/2) + O(n/2),时间复杂度为 O(n * log n); 对于 tree->list-2,T(n) = 2*T(n/2) + O(1),时间复杂度为 O(n),第二个增长的慢一些。
Exercise 2.64
The following procedure list->tree converts an ordered list to a balanced binary tree. The helper procedure partial-tree takes as arguments an integer n and list of at least n elements
and constructs a balanced tree containing the firstn elements of the list. The result returned by partial-tree is a pair (formed with cons) whose car is the constructed tree and
whose cdr is the list of elements not included in the tree.
(define (list->tree elements)
(car (partial-tree elements (length elements))))
(define (partial-tree elts n)
(if (= n 0)
(cons '() elts)
(let ((left-size (quotient (- n 1) 2)))
(let ((left-result
(partial-tree elts left-size)))
(let ((left-tree (car left-result))
(non-left-elts (cdr left-result))
(right-size (- n (+ left-size 1))))
(let ((this-entry (car non-left-elts))
(right-result
(partial-tree
(cdr non-left-elts)
right-size)))
(let ((right-tree (car right-result))
(remaining-elts
(cdr right-result)))
(cons (make-tree this-entry
left-tree
right-tree)
remaining-elts))))))))a. Write a short paragraph explaining as clearly as you can how partial-tree works. Draw the tree produced by list->tree for the list (1 3 5 7 9 11).
b. What is the order of growth in the number of steps required by list->tree to convert a list ofn elements?
a. 这个函数首先取前 (n-1)/2 个元素作为树的左子树,取剩下的元素中第一个作为树的根,然后把剩下的元素作为右子树,对于每一个子树也采用同样的方法,最后把左子树、根和右子树拼起来作为返回结果的第一个元素。
结果如下所示:
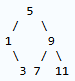
b. partial-tree 每一次都把列表分成2个大概是 n/2 的新列表和中间的一个元素,然后再把他们拼成一颗树。所以 T(n) = 2T(n/2) + O(1),根据 Master theorem,a=2, b=2, f(n) = O(1) = O(n^0), 即 c=0.
则 T(n) = O(n),具体计算方法参考这篇维基百科。