前一章节我们介绍了B树,了解了B树是 适用于大规模数据存储和 磁盘访问的树结构,而今天要讲的B+是B树的一种改进,是B树的一种优化和改进,被大多数据库系统采纳作为索引结构使用。
一、基本概念B+树是B树的改进,因而同样是一种自平衡的多叉树,它更适用于数据库索引。其基本特征如下图表:

一棵正常的B+树,如下图:
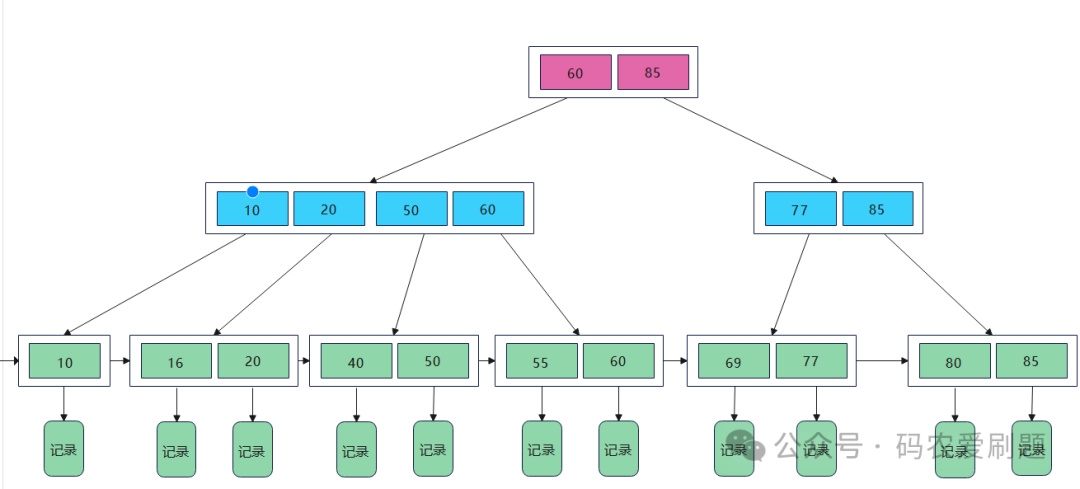
二、B+树的查找
B+树中的所有数据均保存在叶子节点,且根结点和内部节点均只是充当控制查找记录的媒介,并不代表数据本身,所有的内部节点关键字都同时存在于子节点中,是子节点关键字中是值最大(或最小)的。例如在上图中的B+树中查找55这个关键字,步骤如下:
1.在根节点中对比55和根节点中的元素[60, 85],发现55<60,因此应该在第一个节点中继续寻找;
2.同理,比较55和第一个节点中的元素[10, 20, 50, 60],发现50<55<60,因此55应该存在于第四个结点当中;
3.继续对比55和第四个结点中的元素[55, 60],找到55,查找成功。当然,也有查找失败的情况,即要查找的元素并不在B+树中。
三、B+树的插入
B+树的插入和B树十分相似,其插入规则如下:. 插入的操作全部都在叶子节点上进行,且不能破坏关键字自小而大的顺序;
2. 当插入关键字后节点的关键字个数大于m,需要进行"分裂"。B+树的插入有四种情况:
1. 若被插入关键字所在的节点,其含有关键字数目小于m,则直接插入;
2. 若被插入关键字所在的节点,其含有关键字数目等于m,则需要将这个节点分为左右两部分,中间的节点放到父节点中。假设其双亲结点中包含的关键字个数小于m,则插入操作完成。
3. 在第2种情况中,如果上移操作导致其双亲节点中关键字个数大于m,则应继续分裂其双亲节点。
4. 若插入的关键字比当前节点中的最大值还大,破坏了B+树中从根节点到当前节点的所有索引值,此时需要及时修正后,再做其他操作。四、B+树的删除
B+树的删除也和B树十分类似,它同样有下面几种情况:
1. 找到存储有该关键字所在的节点时,由于该节点中关键字个数>=⌈m/2⌉,做删除操作不会破坏B+树,则可以直接删除;
2. 当删除某节点中最大或者最小的关键字,就会涉及到更改其双亲节点一直到根节点中所有索引值的更改。
3. 当删除该关键字,导致当前节点中关键字个数小于 ⌈m/2⌉,若其兄弟节点中含有多余的关键字,可以从兄弟节点中借关键字完成删除操作。
4. 第3种情况中,如果其兄弟节点没有多余的关键字,则需要同其兄弟节点进行合并;当进行合并时,可能会产生因合并使其双亲节点破坏 B+树的结构,需要依照以上规律处理其双亲节点。五、B+树和B树的区别
从以上图表可以看出,B树和B+树的差异主要有以下几点:
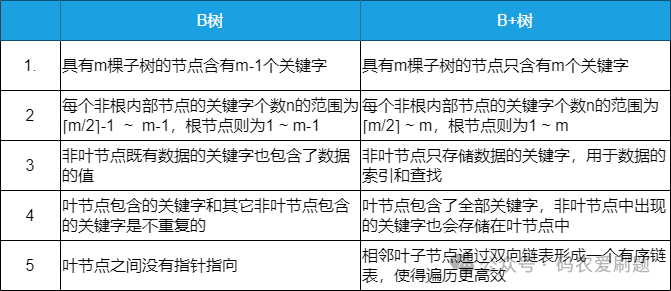
B+ 树的优点在于:
1.由于B+树在非叶子节点上不包含真正的数据,只当做索引使用,因此在内存相同的情况下,能够存放更多的key。
2.B+树的叶子节点都是相连的,因此对整棵树的遍历只需要一次线性遍历叶子节点即可。而且由于数据顺序排列并且相连,所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。
B树的优点在于:
由于B树的每一个节点都包含key和value,因此我们根据key查找value时,只需要找到key所在的位置,就能找到value,但B+树只有叶子节点存储数据,索引每一次查找,都必须一次一次,一直找到树的最大深度处,也就是叶子节点的深度,才能找到value。
六、B+树在数据库中的应用
在数据库的操作中,查询操作可以说是最频繁的一种操作,因此在设计数据库时,必须要考虑到查询的效率问题,在很多数据库中,都是用到了B+树来提高查询的效率;在操作数据库时,我们为了提高查询效率,可以基于某张表的某个字段建立索引,就可以提高查询效率,那其实这个索引就是B+树这种数据结构实现的。
未建立主键索引查询
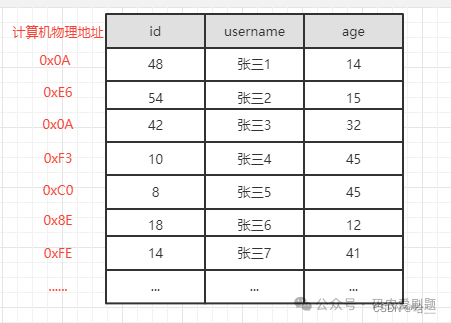
执行 select * from user where id=18 ,需要从第一条数据开始,一直查询到第6条,发现id=18,此时才能查询出目标结果,共需要比较6次;
建立主键索引查询

区间查询
执行 select * from user where id=18 ,所以我们只需要找到id为12的叶子节点,然后按照遍历链表的方式顺序往后查即可,效率非常高。