(⊙﹏⊙)下周有要开组会,不知道该说啥,啊啊啊啊😫
目录
1.基本概念
提到树,我们第一反应都是数据结构中的二叉树,那么决策树又是什么?他有什么特别之处呢?
决策树是一类常见的机器学习算法。按照西瓜书里给出的定义👇:
以二分类任务为例,我们希望从给定的数据集学得一个模型用于对新示例进行分类,这个把样本分类的任务,可以看作对"当前样本属于正类吗?"这个问题的"决策"或"判定"过程。
这个定义看起来还是有些晦涩,通俗的来讲,决策树就是一种依赖树型结构进行决策的模型 。例如,我们买西瓜的时候肯定想挑一个熟透的好瓜,一般来讲我们都有一套判断这个西瓜怎么样的标准,比如拍一拍听西瓜的声音是怎么样的?西瓜的色泽是不是鲜明的等等,我们把每个判断标准作为一个树结点,判断结果作为两个子结点连接下一个判断条件,最终得到叶子结点判断这个瓜是好瓜还是坏瓜。这个构建树并且根据树进行决策的过程就叫做决策树算法。
如下图就是西瓜书中给出的一个例子:
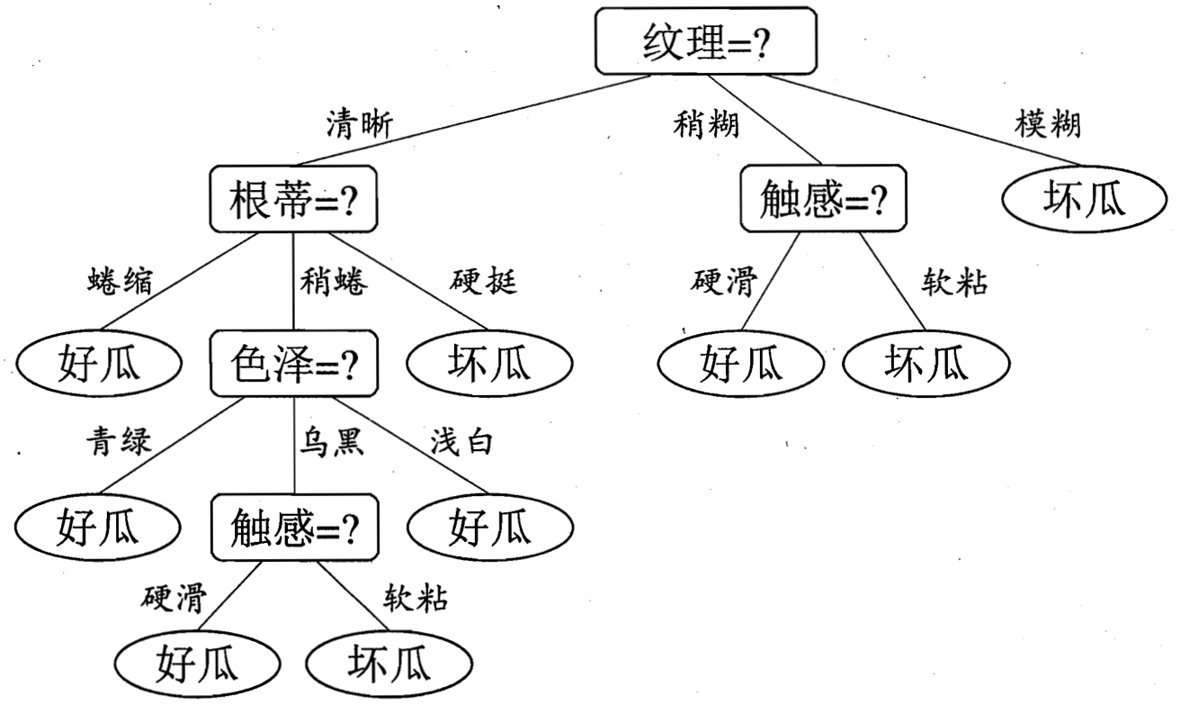
一般的,一颗决策树只包含一个根结点、若干个内部和若干个叶结点;叶结点对应于决策的结果,其他每个结点则对应于一个属性测试;每个结点包含包含的样本集合根据属性测试的结果被划分到子结点中;根节点包含样本全集。算法流程用伪代码可以描述为:
python
Input: 训练样本集D={(x1,y1),(x2,y2)......(xn,yn)}
属性集A={a1,a2,......,an}
TreeGenerate(D,A):
生成节点node
if D中样本全属于同一类别C:
将node标记为C类叶节点
return
end if
if 属性集A为空或者D的所有属性值均一样:
将node标记为最多类
return
end if
从A中选取最佳划分属性a*
for a in a*:
为node生成一个分支,令Dv表示D中在a*属性值为a的样本子集
if Dv为空:
continue;
else:
TreeGenerate(Dv,A\{a*})递归继续
end if
end for
显然,决策树的生成是一个递归过程。决策树基本算法中,有三种情况会导致递归返回:
- 当前结点包含的样本全属于同一类别,无需划分;
- 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分;
- 当前结点包含的样本集合为空,不能划分。
2.ID3算法
ID3 算法是建立在奥卡姆剃刀(用较少的东西,同样可以做好事情)的基础上:越是小型的决策树越优于大的决策树。
构造一棵优秀的决策树关键在于划分最优属性,也就是我们希望决策树的分支结点尽可能的属于同一类别,即结点的"纯度"越来越高。
ID3算法就是从这一角度出发,核心思想就是计算样本集合的信息熵 (从信息论的知识中我们知道:信息熵越大,从而样本纯度越低)以划分属性后的信息增益来度量特征选择 ,选择信息增益最大的特征进行分裂。算法采用自顶向下的贪婪搜索遍历可能的决策树空间(C4.5 也是贪婪搜索)。
假定当前样本集合 D 中第 k 类样本所占的比例为 pk(k=1,2...,∣γ),则 D 的信息熵定义为:

Ent(D) 的值越小,则 D 的纯度越高。
然而我们还应考虑一点,根据离散属性 a 进行划分后,各个结点包含的样本数不同,理论上每个分支节点的权重也应该不同,所以应给各分支点赋予权重 。于是我们可以计算中用属性 a 进行划分得到的**"信息增益"(information gain)**

其中 V 表示离散属性 a 的 V 个可能取值,其中第 v 个分支结点包含了 D 中所有在属性 a 上取值为 的样本,记为
。
信息增益越大表示使用特征 A 来划分所获得的**"纯度提升越大"**。
算法实例
我们以西瓜书中的西瓜数据集2.0为例,该数据集包含17个训练样例:
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 2 | 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 3 | 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 4 | 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 5 | 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 6 | 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 7 | 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 是 |
| 8 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 9 | 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
| 10 | 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 否 |
| 11 | 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 12 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 否 |
| 13 | 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 14 | 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 15 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 否 |
| 16 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
| 17 | 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
根结点包含 D 中所有的样例,其中正例占p1=8/17,反例p1=8/15,于是可以计算出根结点的信息熵为:

我们首先要确定第一个划分属性,因此需要计算每个属性的信息增益做对比取最大值,这里我们以"色泽"为例,它有三个可能的取值:{青绿,乌黑,浅白},经过划分后可以得到三个子集,分别为

子集 D1 中的正例有3个,反例有3个,子集 D2 中的正例有4个,反例有2个,子集 D3 中的正例有1个,反例有4个。计算3个分支结点的信息熵得:

于是可以计算出属性"色泽"的信息增益为:

我们可以计算出类似的其他属性的信息增益:
显然,属性"纹理"的信息增益最大,于是它被选为划分属性。
剩下的操作类似,直至构造出一棵完整的决策树。

那到这里为止,我们已经知道了构建树的算法,上面也说了有了树,我们直接遍历决策树就能得到我们预测样例的类别。
性能评价
优点:
- 1.假设空间包含所有的决策树,搜索空间完整。
- 2.健壮性好,不受噪声影响。
- 3.可以训练缺少属性值的实例。
缺点:
- ID3 没有剪枝策略,容易过拟合;
- 信息增益准则对可取值数目较多的特征有所偏好,类似"编号"的特征其信息增益接近于 1;
- 只能用于处理离散分布的特征;
- 没有考虑缺失值。
3.C4.5算法
C4.5 相对于 ID3 的缺点对应有以下改进方式:
- 引入悲观剪枝策略进行后剪枝;
- 引入信息增益率作为划分标准;
- 将连续特征离散化,假设 n 个样本的连续特征 A 有 m 个取值,C4.5 将其排序并取相邻两样本值的平均数共 m-1 个划分点,分别计算以该划分点作为二元分类点时的信息增益,并选择信息增益最大的点作为该连续特征的二元离散分类点;
- 对于缺失值的处理可以分为两个子问题:
- 问题一:在特征值缺失的情况下进行划分特征的选择?(即如何计算特征的信息增益率)
- 问题二:选定该划分特征,对于缺失该特征值的样本如何处理?(即到底把这个样本划分到哪个结点里)
- 针对问题一,C4.5 的做法是:对于具有缺失值特征,用没有缺失的样本子集所占比重来折算;
- 针对问题二,C4.5 的做法是:将样本同时划分到所有子节点,不过要调整样本的权重值,其实也就是以不同概率划分到不同节点中。
算法思想
ID3 算法,算法的核心思想是划分后每个子集的元素尽量都属于一个类别,那么如果我们把样本"编号"也当作一种属性考虑会是什么情况呢?
若以"编号"作为划分属性,我们可以得到17个分支,并且计算它的信息增益发现"编号''的信息增益居然是最大的,原高于其他的属性,那么我们是否可以选则"编号"作为我们的划分属性呢?用常识思考一下就会发现这种划分是没有任何意义的,这样的决策树不具备泛化能力,是根本无法对新样本进行有效预测的。
因此避免信息增益准测对可取值数目多的属性产生偏好,著名的 C4.5 决策树算法没有直接采用信息增益,可以使用了"增益率"这一概念来划分最优属性。增益率定义为:

IV(a) 称为属性 a 的"固有值",属性 a 的可能取值数目越多,则 IV(a) 的值越大。

这里需要注意,信息增益率对可取值较少的特征有所偏好(分母越小,整体越大),因此 C4.5 并不是直接用增益率最大的特征进行划分,而是使用一个启发式方法:先从候选划分特征中找到信息增益高于平均值的特征,再从中选择增益率最高的。
性能评价
优点:
- 产生的规则易于理解;准确率较高;实现简单;
- 解决了偏向子类别多的特征的问题;
- 解决了 ID3 算法无法处理连续变量的问题;
缺点;
- 对数据进行多次顺序扫描和排序,效率较低;
- 只适合小规模数据集,需要将数据放到内存中
4.CART算法
ID3 和 C4.5 虽然在对训练样本集的学习中可以尽可能多地挖掘信息,但是其生成的决策树分支、规模都比较大,CART 算法的二分法可以简化决策树的规模,提高生成决策树的效率。
算法思想
CART 包含的基本过程有分裂,剪枝和树选择。
- 分裂: 分裂过程是一个二叉递归划分过程,其输入和预测特征既可以是连续型的也可以是离散型的,CART 没有停止准则,会一直生长下去;
- 剪枝: 采用代价复杂度剪枝,从最大树开始,每次选择训练数据熵对整体性能贡献最小的那个分裂节点作为下一个剪枝对象,直到只剩下根节点。CART 会产生一系列嵌套的剪枝树,需要从中选出一颗最优的决策树;
- 树选择: 用单独的测试集评估每棵剪枝树的预测性能(也可以用交叉验证)。
CART 在 C4.5 的基础上进行了很多提升。
- C4.5 为多叉树,运算速度慢,CART 为二叉树,运算速度快;
- C4.5 只能分类,CART 既可以分类也可以回归;
- CART 使用 Gini 系数作为变量的不纯度量,减少了大量的对数运算;
- CART 采用代理测试来估计缺失值,而 C4.5 以不同概率划分到不同节点中;
- CART 采用"基于代价复杂度剪枝"方法进行剪枝,而 C4.5 采用悲观剪枝方法。
划分标准
CART决策树使用了"基尼指数"来选择划分属性,基尼指数反映了从数据集中随机抽取两个样本,其类别标记不一致的概率。因此基尼指数越小,则数据集纯度越高。基尼指数偏向于特征值较多的特征,类似信息增益。基尼指数可以用来度量任何不均匀分布,是介于 0~1 之间的数,0 是完全相等,1 是完全不相等。

其中 k 代表类别,Ck 表示属于 k 类别的样本数,属性 a 的基尼指数定义为:

于是我们在候选属性集合 A 中,选择那个划分后基尼指数最小的属性作为最优划分属性。
剪枝策略
CART算法采用一种"基于代价复杂度的剪枝"方法进行后剪枝,这种方法会生成一系列树,每个树都是通过将前面的树的某个或某些子树替换成一个叶节点而得到的,这一系列树中的最后一棵树仅含一个用来预测类别的叶节点。
然后用一种成本复杂度的度量准则来判断哪棵子树应该被一个预测类别值的叶节点所代替。这种方法需要使用一个单独的测试数据集来评估所有的树,根据它们在测试数据集熵的分类性能选出最佳的树。
类别不平衡问题
CART 的一大优势在于:无论训练数据集有多失衡,它都可以将其子冻消除不需要建模人员采取其他操作。
CART 使用了一种先验机制,其作用相当于对类别进行加权。这种先验机制嵌入于 CART 算法判断分裂优劣的运算里,在 CART 默认的分类模式中,总是要计算每个节点关于根节点的类别频率的比值,这就相当于对数据自动重加权,对类别进行均衡。
对于一个二分类问题,节点 node 被分成类别 1 当且仅当:

比如二分类,根节点属于 1 类和 0 类的分别有 20 和 80 个。在子节点上有 30 个样本,其中属于 1 类和 0 类的分别是 10 和 20 个。如果 10/20>20/80,该节点就属于 1 类。
通过这种计算方式就无需管理数据真实的类别分布。假设有 K 个目标类别,就可以确保根节点中每个类别的概率都是 1/K。这种默认的模式被称为"先验相等"。
先验设置和加权不同之处在于先验不影响每个节点中的各类别样本的数量或者份额。先验影响的是每个节点的类别赋值和树生长过程中分裂的选择。
5.连续与缺失值处理
我们上述描述的例子都是基于数据比较优质,可以直接拿来分析处理。然而一般情况下我们采集到的数据都或多或少存在一些问题,比如数据缺失,这种情况下我们需要先对数据进行一些处理才能进行决策树的构建。
5.1.连续值处理
到目前为止我们仅讨论了基于离散属性 来生成决策树,现实学习任务中常常遇到连续属性,有必要讨论如何在决策树学习中使用连续属性。我们将相邻的两个属性值的平均值作为候选点。
基本思路:连续属性离散化。
常见的简单做法:二分法(这正是C4.5决策树算法中采用的机制)。
对于连续属性 a,我们可考察包括 n−1 个元素的候选划分集合( n 个属性值可形成 n−1 个候选点):
我们以西瓜数据集做个示范;
| 密度 | 含糖率 | 好瓜 |
|---|---|---|
| 0.697 | 0.460 | 是 |
| 0.774 | 0.376 | 是 |
| 0.634 | 0.264 | 是 |
| 0.608 | 0.318 | 是 |
| 0.556 | 0.215 | 是 |
| 0.403 | 0.237 | 是 |
| 0.481 | 0.149 | 是 |
| 0.437 | 0.211 | 是 |
| 0.666 | 0.091 | 否 |
| 0.243 | 0.267 | 否 |
| 0.245 | 0.057 | 否 |
| 0.343 | 0.099 | 否 |
| 0.639 | 0.161 | 否 |
| 0.657 | 0.198 | 否 |
| 0.360 | 0.370 | 否 |
| 0.593 | 0.042 | 否 |
| 0.719 | 0.103 | 否 |
对于数据集中的属性"密度",在决策树开始学习时,根节点包含的17个训练样本在该属性上取值均不同。该属性的候选划分点集合包括16个候选值:
- 密度={0.244,0.294,0.351,0.381,0.42.,0.459,0.518,0.574,0.600,0.621,0.636,0.648,0.661,0.681,0.708,0.746}T密度={0.244,0.294,0.351,0.381,0.42.,0.459,0.518,0.574,0.600,0.621,0.636,0.648,0.661,0.681,0.708,0.746}
计算可知属性"密度"信息增益为0.262,对应划分点0.381.
对属性"含糖率",其候选划分点集合也包括16个候选值:
- 含糖率={0.049,0.074,0.095,0.101,0.126,0.155,0.179,0.204,0.213,0.226,0.250,0.265,0.292,0.344,0.373,0.418}T含糖率={0.049,0.074,0.095,0.101,0.126,0.155,0.179,0.204,0.213,0.226,0.250,0.265,0.292,0.344,0.373,0.418}
计算可知其信息增益为0.349,对应于划分点0.126.
类似的,计算得到的各属性的信息增益值:

比较能够知道纹理的信息增益值最大,因此,"纹理"被选作根节点划分属性,下面只要重复上述过程递归的进行,就能构造出一颗决策树:
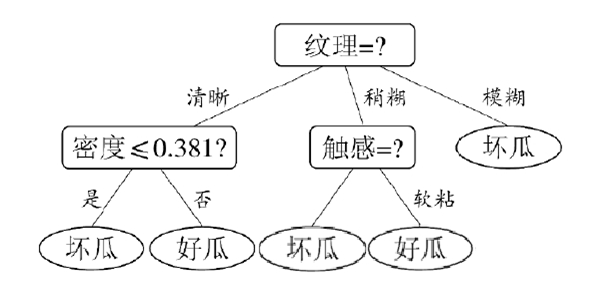
有一点需要注意的是:与离散属性不同,若当前结点划分属性为连续属性,该属性还可作为其后代结点的划分属性。什么意思呢?就是例如我们上面这颗决策树以连续变量密度 ≤0.381 作为一个结点,那么这个结点的后代结点我还可以用这个属性划分,比如后面添加一个密度 ≤0.2 的结点。
5.2.缺失值处理
现实任务中常会遇到不完整样本,即样本的某些属性值缺失。如果简单地放弃不连续样本,仅使用无缺值样本来进行学习,显然是对数据信息极大的浪费。显然我们有必要考虑利用有缺失属性值的训练样例来进行学习。
在决策树中处理含有缺失值的样本的时候,需要解决两个问题:
- 如何在属性值缺失的情况下进行划分属性的选择?(比如"色泽"这个属性有的样本在该属性上的值是缺失的,那么该如何计算"色泽"的信息增益?)
对于第一个问题,假如你使用ID3算法,那么选择分类属性时,就要计算所有属性的熵增(信息增益,Gain)。假设10个样本,属性是a,b,c。在计算a属性熵时发现,第10个样本的a属性缺失,那么就把第10个样本去掉,前9个样本组成新的样本集,在新样本集上按正常方法计算a属性的熵增。然后结果乘0.9(新样本占raw样本的比例),就是a属性最终的熵。
- 给定划分属性,若样本在该属性上的值是缺失的,那么该如何对这个样本进行划分?(即到底把这个样本划分到哪个结点里?)
比如该节点是根据a属性划分,但是待分类样本a属性缺失,怎么办呢?假设a属性离散,有1,2两种取值,那么就把该样本分配到两个子节点中去,但是权重由1变为相应离散值个数占样本的比例。然后计算错误率的时候,注意,不是每个样本都是权重为1,存在分数。
6.剪枝处理
剪枝(pruning)是决策树学习算法用于处理"过拟合"的重要手段,有关过拟合的概念我们以及在上一个 level 做了简单的解释。在决策树算法中,所谓的过拟合是指因为结点划分过程中分支过多 ,以至于把训练集自己的一些特点当作所以样本的一般特征导致的过拟合。因此可以考虑通过去掉一些分支来降低过拟合风险。
6.1.预剪枝策略
决策树剪枝的策略可以分为预剪枝、后剪枝两类。
预剪枝指在每个结点划分前就进行估计,考虑结点对于整体划分效果是否有提升。如果当前结点的划分不能对决策树泛化性能有提高吗,则停止划分并将当前结点标记为叶结点。
总结:边构造边剪枝。
我们这里根据前面小节的西瓜数据集举一个预剪枝操作的例子:
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 2 | 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 3 | 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 4 | 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 5 | 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 6 | 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 7 | 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 是 |
| 8 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 9 | 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
| 10 | 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 否 |
| 11 | 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 12 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 否 |
| 13 | 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 14 | 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 15 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 否 |
| 16 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
| 17 | 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
- 首先,基于信息增益准则,我们计算每个属性值得信息增益发现 "脐部" 的信息增益最大,因此我们选择 "脐部" 作为划分属性。
- 然后,考虑是否要按照"脐部"划分。在划分前,只有一个根节点,也是叶子节点,标记为"好瓜"。通过测试集验证,只有{4,5,8}3个样本可以正确分类,精度为 37×100%=42.9%73×100%=42.9% 。当按照脐部划分后,再进行验证,发现{4,5,8,11,12}被正确分类,精度为 57×100%=71.5%75×100%=71.5% 。精度提高,所以按照"脐部"进行划分。
- 当按照脐部进行划分后,会对结点 (2) 进行划分,再次使用信息增益挑选出值最大的那个特征,信息增益值最大的那个特征是"色泽",则使用"色泽"划分后决策树为。但是,使用"色泽"划分后,编号为{5}的样本会从"好瓜"被分类为"坏瓜",只有{4,8,11,12}被正确分类,精确度为 47×100%=57.1%74×100%=57.1% 。所以,预剪枝操作会不再被这个节点进行划分。
- 对于节点(3),最优属性为"根蒂"。但是,这么划分后精确度仍然是 71.4% ,所以也不会对这个节点进行操作。
预剪枝得到的决策树如下图所示。
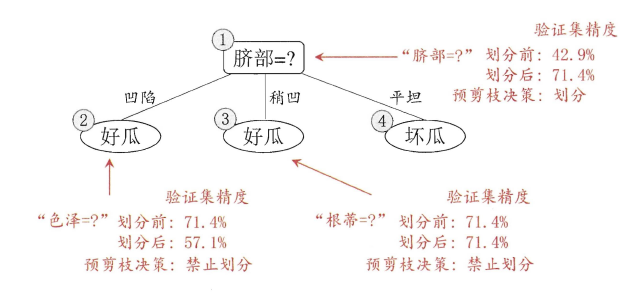
**评价:**预剪枝基于 "贪心" 本质禁止这些分支展开,虽然降低了 "过拟合" 的风险,节省了决策树训练的时间开销,但另一方面有些直接去掉的分支虽然暂时不能给决策树带来性能上的提升,但是他们的后续结点未必会是这样,给预剪枝决策树带来了 "欠拟合" 的风险。
6.2.后剪枝策略
后剪枝则是先从训练集中生成一棵完整的决策树,然后自底向上的考察每一个非叶结点,和预剪枝相反,如果将该结点对应的子树替换为叶结点能给决策树带来性能上的提升,则将该子树替换为叶结点。
总结:构造完再剪枝。
我们根据上面给出的数据集根据信息增益构造出一棵决策树:
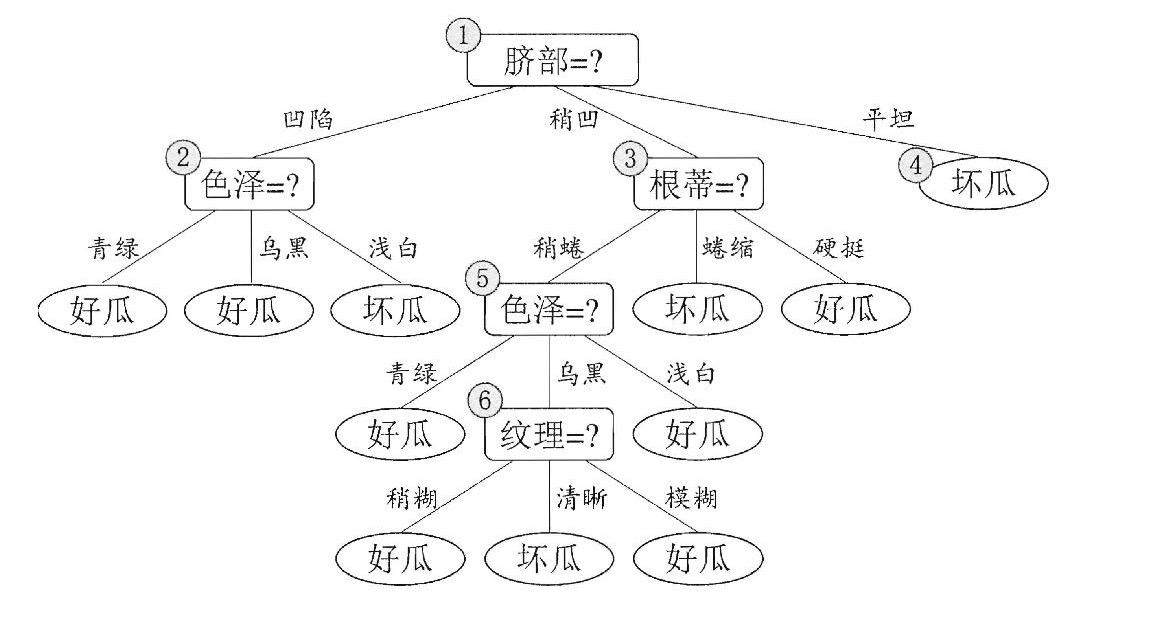
- 后剪枝算法首先考察上图中的结点 (6),若将以其为根节点的子树删除,即相当于把结点 (6) 替换为叶结点,替换后的叶结点包括编号为{7,15}的训练样本,因此把该叶结点标记为"好瓜"(因为这里正负样本数量相等,所以随便标记一个类别),因此此时的决策树在验证集上的精度为57.1%57.1%(未剪枝的决策树为 42.9%42.9%),所以后剪枝策略决定剪枝。
- 接着考察结点 5,同样的操作,把以其为根节点的子树替换为叶结点,替换后的叶结点包含编号为{6,7,15}的训练样本,根据"多数原则"把该叶结点标记为"好瓜",测试的决策树精度认仍为 57.1%57.1% ,所以不进行剪枝。
- 考察结点 2 ,和上述操作一样,不多说了,叶结点包含编号为{1,2,3,14}的训练样本,标记为"好瓜",此时决策树在验证集上的精度为 71.4%71.4% ,因此,后剪枝策略决定剪枝。
- 接着考察结点 3 ,同样的操作,剪枝后的决策树在验证集上的精度为 71.4%71.4% ,没有提升,因此不剪枝;对于结点 1 ,剪枝后的决策树的精度为 42.9%42.9% ,精度下降,因此也不剪枝。
因此,基于后剪枝策略生成的最终的决策树如下图所示,其在验证集上的精度为 71.4%71.4% 。
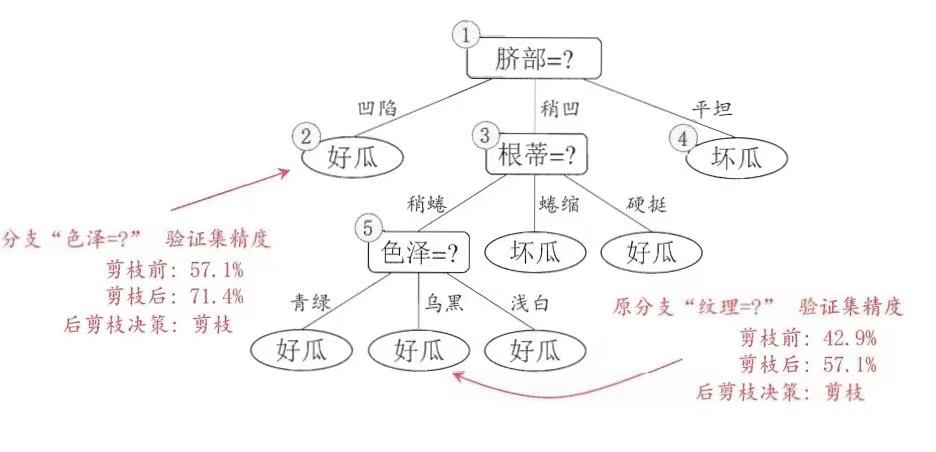
**评价:**对比预剪枝和后剪枝,能够发现,后剪枝决策树通常比预剪枝决策树保留了更多的分支,一般情形下,后剪枝决策树的欠拟合风险小,泛华性能往往也要优于预剪枝决策树。但后剪枝过程是在构建完全决策树之后进行的,并且要自底向上的对树中的所有非叶结点进行逐一考察,因此其训练时间开销要比未剪枝决策树和预剪枝决策树都大得多。
7.实例代码
1.计算经验熵值
python
#1.calcShannonEnt函数说明:计算给定数据集的经验熵(香农熵)
#Parameters: dataSet:数据集
#Returns: shannonEnt:经验熵
def calcShannonEnt(dataSet):
# 返回数据集行数
numEntries = len(dataSet)
# 获取数据集的样本数量,用于后续计算每个标签出现的概率等操作
# 保存每个标签(label)出现次数的字典
labelCounts = {}
# 创建一个空字典,用于统计每个标签在数据集中出现的次数
# 对每组特征向量进行统计
for featVec in dataSet:
currentLabel = featVec[-1] # 提取标签信息
# 对于数据集中的每个特征向量,提取其最后一个元素作为当前标签
if currentLabel not in labelCounts.keys(): # 如果标签没有放入统计次数的字典,添加进去
labelCounts[currentLabel] = 0
# 如果当前标签不在统计字典中,将其添加并初始化为0
labelCounts[currentLabel] += 1 # label计数
# 对当前标签的出现次数加1,表示又出现了一次该标签
shannonEnt = 0.0 # 经验熵
# 初始化经验熵的值为0.0,后续将根据标签出现的概率来计算其具体值
# 计算经验熵
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries # 选择该标签的概率
# 计算每个标签在数据集中出现的概率,即该标签出现的次数除以数据集的总行数
shannonEnt -= prob * log(prob, 2) # 利用公式计算
# 根据香农熵的计算公式H = -Σp(x)log₂p(x),将每个标签的概率乘以其对数(以2为底)并累加到shannonEnt中(注意这里是减去,因为公式前面有个负号)
return shannonEnt # 返回经验熵
# 函数执行完毕后,返回计算得到的经验熵值shannonEnt2.创建数据集
python
#2.createDataSet函数说明:创建测试数据集
#Parameters:无
#Returns: dataSet:数据集
# labels:分类属性
def createDataSet():
# 数据集
dataSet = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
# 创建一个二维列表作为数据集,每个子列表代表一个数据样本,最后一个元素是该样本的分类标签('yes'或'no'),前面的元素是该样本的各种特征值
# 分类属性
labels = ['年龄', '有工作', '有自己的房子', '信贷情况']
# 创建一个列表,包含了数据集中每个特征对应的名称,用于后续对数据和决策树的理解和操作
# 返回数据集和分类属性
return dataSet, labels
# 函数执行完毕后,返回创建好的数据集dataSet和对应的分类属性列表labels3.splitDataSet函数说明:按照给定特征划分数据集
python
#3.splitDataSet函数说明:按照给定特征划分数据集
#Parameters: dataSet:待划分的数据集
# axis:划分数据集的特征
# value:需要返回的特征值
#Returns: 无
def splitDataSet(dataSet, axis, value):
# 创建返回的数据集列表
retDataSet = []
# 创建一个空列表,用于存储划分后符合条件的数据样本,它将作为函数的返回值
# 遍历数据集
for featVec in dataSet:
if featVec[axis] == value:
# 对于数据集中的每个特征向量,检查其在指定的特征索引axis处的值是否等于给定的特征值value,如果相等,则说明该样本符合划分条件,需要进行后续处理
# 去掉axis特征
reduceFeatVec = featVec[:axis]
# 创建一个新的列表,它包含了原特征向量featVec中指定特征索引axis之前的所有元素,即去掉了指定特征
# 将符合条件的添加到返回的数据集
reduceFeatVec.extend(featVec[axis + 1:])
# 将原特征向量featVec中指定特征索引axis之后的所有元素添加到reduceFeatVec中,这样就得到了一个去掉指定特征的新特征向量
retDataSet.append(reduceFeatVec)
# 将处理好的新特征向量reduceFeatVec添加到retDataSet列表中,该列表最终将包含所有符合划分条件的样本
# 返回划分后的数据集
return retDataSet
# 函数执行完毕后,返回划分后的数据集retDataSet4.chooseBestFeatureToSplit函数说明:计算给定数据集的经验熵(香农熵)
python
#4.chooseBestFeatureToSplit函数说明:计算给定数据集的经验熵(香农熵)
#Parameters: dataSet:数据集
#Returns: shannonEnt:信息增益最大特征的索引值
def chooseBestFeatureToSplit(dataSet):
# 特征数量
numFeatures = len(dataSet[0]) - 1
# 获取数据集中每个样本的特征数量,通过取数据集中第一个样本的长度并减去1(因为最后一个元素是标签)来得到
# 计数数据集的香农熵
baseEntropy = calcShannonEnt(dataSet)
# 调用calcShannonEnt函数计算数据集的初始香农熵,即未考虑任何特征划分时的熵值,将其作为基础熵值保存起来,用于后续计算信息增益
# 信息增益
bestInfoGain = 0.0
# 初始化信息增益的最大值为0.0,后续将在遍历特征的过程中不断更新这个值,以找到最大的信息增益
# 最优特征的索引值
bestFeature = -1
# 初始化最优特征的索引值为 -1,同样在遍历特征过程中,当找到信息增益最大的特征时,将更新这个值为该特征的实际索引
# 遍历所有特征
for i in range(numFeatures):
# 循环变量i从0到特征数量减1,代表每个特征的索引,开始遍历数据集中的每一个特征
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
# 对于当前遍历到的特征索引i,创建一个列表featList,它包含了数据集中每个样本在该特征索引处的值,即提取了数据集中所有样本的第i个特征的值
# 创建set集合{},元素不可重复
uniqueVals = set(featList)
# 将featList转换为集合uniqueVals,集合中的元素具有唯一性,这样就可以得到该特征所有可能出现的不同值,用于后续根据不同值划分数据集并计算条件熵
# 经验条件熵
newEntropy = 0.0
# 初始化经验条件熵的值为0.0,用于在后续根据不同特征值划分数据集后计算条件熵,并累加到这个变量中
# 计算信息增益
for value in uniqueVals:
# 遍历当前特征的所有不同值,即遍历集合uniqueVals中的每个元素
# subDataSet划分后的子集
subDataSet = splitDataSet(dataSet, i, value)
# 对于当前特征的每个不同值value,调用splitDataSet函数根据该特征值对数据集进行划分,得到划分后的子集subDataSet
# 计算子集的概率
prob = len(subDataSet) / float(len(dataSet))
# 计算划分后得到的子集subDataSet在原数据集中所占的比例,即该子集出现的概率,通过子集的长度除以原数据集的长度来得到
# 根据公式计算经验条件熵
newEntropy += prob * calcShannonEnt((subDataSet)) # 调用calcShannonEnt
# 根据条件熵的计算公式,将子集出现的概率乘以该子集的香农熵(通过调用calcShannonEnt函数计算得到),并累加到newEntropy中,这样就逐步计算出了基于当前特征的经验条件熵
# 信息增益
infoGain = baseEntropy - newEntropy # 计算信息增益
# 根据信息增益的计算公式"信息增益 = 基础熵 - 条件熵",用之前计算得到的基础熵baseEntropy减去当前特征的经验条件熵newEntropy,得到当前特征的信息增益infoGain
# 打印每个特征的信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain))
# 打印出当前特征的信息增益值,方便查看每个特征对分类的贡献程度,格式为"第特征索引个特征的增益为具体增益值",其中具体增益值保留三位小数
# 计算信息增益
if (infoGain > bestInfoGain):
# 检查当前特征的信息增益是否大于之前记录的最大信息增益bestInfoGain,如果大于,则说明找到了一个信息增益更大的特征
# 更新信息增益,找到最大的信息增益
bestInfoGain = infoGain
# 如果当前特征的信息增益更大,就更新最大信息增益的值为当前特征的信息增益值
# 记录信息增益最大的特征的索引值
bestFeature = i
# 同时更新最优特征的索引值为当前特征的索引i,表2024-11-07 0:00:00示当前特征是目前找到的信息增益最大的特征
# 返回信息增益最大特征的索引值
return bestFeature
# 函数执行完毕后,返回信息增益最大特征的索引值bestFeature5.createTree函数说明:创建决策树
python
#5.createTree函数说明:创建决策树
#Parameters: dataSet:训练数据集
# labels:分类属性标签
# featLabels:存储选择的最优特征标签
#Returns: myTree:决策树
def createTree(dataSet, labels, featLabels):
# 取分类标签(是否放贷:yes or no)
classList = [example[-1] for example in dataSet]
# 创建一个列表classList,它包含了数据集中每个样本的分类标签,通过提取每个样本的最后一个元素得到,用于后续判断数据集中的类别是否完全相同
# 如果类别完全相同,则停止继续划分
if classList.count(classList[0]) == len(classList):
return classList[0]
# 检查classList中第一个元素出现的次数是否等于列表的长度,如果相等,说明数据集中所有样本的分类标签都相同,此时不需要再继续划分数据集创建决策树,直接返回该相同的分类标签即可
# 选择最优特征
bestFeat = chooseBestFeatureToSplit(dataSet)
# 调用chooseBestFeatureToSplit函数,在给定的数据集中选择信息增益最大的特征,并将该特征的索引值赋给bestFeat,这个特征将作为当前划分数据集创建决策树的最优特征
# 最优特征的标签
bestFeatLabel = labels[bestFeat]
# 根据最优特征的索引值bestFeat,从分类属性标签列表labels中获取该最优特征对应的标签,将其赋给bestFeatLabel
featLabels.append(bestFeatLabel)
# 将最优特征的标签添加到featLabels列表中,用于记录在创建决策树过程中已经选择过的最优特征标签
# 根据最优特征的标签生成树
myTree = {bestFeatLabel: {}}
# 根据最优特征的标签创建一个字典myTree,并将其初始化为一个以最优特征标签为键,值为空字典的结构,这个字典将逐步构建成完整的决策树
# 删除已经使用的特征标签
del(labels[bestFeat])
# 从分类属性标签列表labels中删除已经被选为最优特征的那个标签,因为在后续递归创建决策树时,不需要再考虑这个已经使用的特征
# 得到训练集中所有最优特征的属性值
featValues = [example[bestFeat] for example in dataSet]
# 创建一个列表featValues,它包含了数据集中每个样本在最优特征索引处的值,即获取了训练集中所有最优特征的属性值,用于后续根据这些属性值进一步划分数据集并递归创建决策树
# 去掉重复的属性值
uniqueVls = set(featValues)
# 将featValues转换为集合uniqueVls,得到最优特征所有可能出现的不同属性值,集合中的元素具有唯一性,这样可以根据这些不同值分别划分数据集并递归创建决策树
# 遍历特征,创建决策树
for value in uniqueVls:
myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet, bestFeat, value),
labels, featLabels) # 递归调用createTree
# 遍历最优特征的所有不同属性值。对于每个属性值value,首先调用splitDataSet函数根据最优特征和该属性值对数据集进行划分,得到划分后的数据集。然后递归调用createTree函数,使用划分后的数据集、更新后的分类属性标签列表labels和已经记录的最优特征标签列表featLabels继续创建决策树,并将创建好的子决策树作为当前决策树字典myTree中以最优特征标签为键,以该属性值为键的子字典的值
return myTree
# 函数执行完毕后,返回创建好的完整决策树myTree6.决策树分类
python
#6.使用决策树进行分类
#Parameters: inputTree;已经生成的决策树
# #featLabels:存储选择的最优特征标签
#testVec:测试数据列表,顺序对应最优特征标签
#Returns: classLabel:分类结果
def classify(inputTree, featLabels, testVec):
# 获取决策树节点
firstStr = next(iter(inputTree))
# 获取决策树的根节点的键,即决策树字典中的第一个键,通过将决策树字典转换为迭代器并获取下一个元素得到,这个键通常是在创建决策树时选择的第一个最优特征的标签
# 下一个字典
secondDict = inputTree[firstStr]
# 根据根节点的键firstStr,从决策树字典inputTree中获取对应的值,这个值是一个字典,它包含了根据根节点特征的不同取值划分出的子决策树或分类结果等信息
featIndex = featLabels.index(firstStr)
# 根据最优特征的标签firstStr在featLabels列表中的索引,确定测试数据中对应特征的索引位置
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
# 如果当前节点的值是一个字典,说明还需要继续递归向下分类,再次调用classify函数,传入当前子字典、featLabels和测试数据,继续进行分类操作
else: classLabel = secondDict[key]
# 如果当前节点的值不是字典,说明已经到达叶子节点,直接返回该节点的值作为分类结果
return classLabel
# 函数执行完毕后,返回分类结果classLabel7.主函数
python
#7.main函数说明:主函数
if __name__ == '__main__':
dataSet, labels = createDataSet()
# 调用createDataSet函数创建数据集和对应的分类属性标签列表
featLabels = []
# 创建一个空的featLabels列表,用于存储在创建决策树过程中选择的最优特征标签
myTree = createTree(dataSet, labels, featLabels) # 生成决策树模型
# 调用createTree函数,使用创建好的数据集、分类属性标签和空的featLabels列表来生成决策树模型,并将生成的决策树赋值给myTree
# 测试数据
testVec = [0, 1]
# 创建一个测试数据列表testVec,用于后续对生成的决策树进行测试分类
result = classify(myTree, featLabels, testVec) # 测试样本
# 调用classify函数,使用生成的决策树、存储最优特征标签的featLabels列表和测试数据testVec对测试样本进行分类,并将分类结果赋值给result
if result == 'yes':
print('放贷')
# 如果分类结果为'yes',则打印出'放贷',表示根据决策树的分类结果,应该进行放贷操作
if result == 'no':
print('不放贷')完整代码:
python
import sys
# 导入系统相关的模块,可用于处理命令行参数、标准输出等操作,但在此代码中暂未明显用到
from math import log
# 从math模块中导入log函数,用于后续计算香农熵时的对数运算
import operator
# 导入operator模块,可能用于一些比较、操作等功能,不过这里暂时未明确用到其特定功能
import numpy as np
# 导入numpy库并别名为np,常用于数值计算、数组操作等,目前代码中未明显体现其作用
import pandas as pd
# 导入pandas库并别名为pd,主要用于数据处理和分析,同样目前代码中未明显看到其具体用途
#1.calcShannonEnt函数说明:计算给定数据集的经验熵(香农熵)
#Parameters: dataSet:数据集
#Returns: shannonEnt:经验熵
def calcShannonEnt(dataSet):
# 返回数据集行数
numEntries = len(dataSet)
# 获取数据集的样本数量,用于后续计算每个标签出现的概率等操作
# 保存每个标签(label)出现次数的字典
labelCounts = {}
# 创建一个空字典,用于统计每个标签在数据集中出现的次数
# 对每组特征向量进行统计
for featVec in dataSet:
currentLabel = featVec[-1] # 提取标签信息
# 对于数据集中的每个特征向量,提取其最后一个元素作为当前标签
if currentLabel not in labelCounts.keys(): # 如果标签没有放入统计次数的字典,添加进去
labelCounts[currentLabel] = 0
# 如果当前标签不在统计字典中,将其添加并初始化为0
labelCounts[currentLabel] += 1 # label计数
# 对当前标签的出现次数加1,表示又出现了一次该标签
shannonEnt = 0.0 # 经验熵
# 初始化经验熵的值为0.0,后续将根据标签出现的概率来计算其具体值
# 计算经验熵
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries # 选择该标签的概率
# 计算每个标签在数据集中出现的概率,即该标签出现的次数除以数据集的总行数
shannonEnt -= prob * log(prob, 2) # 利用公式计算
# 根据香农熵的计算公式H = -Σp(x)log₂p(x),将每个标签的概率乘以其对数(以2为底)并累加到shannonEnt中(注意这里是减去,因为公式前面有个负号)
return shannonEnt # 返回经验熵
# 函数执行完毕后,返回计算得到的经验熵值shannonEnt
#2.createDataSet函数说明:创建测试数据集
#Parameters:无
#Returns: dataSet:数据集
# labels:分类属性
def createDataSet():
# 数据集
dataSet = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
# 创建一个二维列表作为数据集,每个子列表代表一个数据样本,最后一个元素是该样本的分类标签('yes'或'no'),前面的元素是该样本的各种特征值
# 分类属性
labels = ['年龄', '有工作', '有自己的房子', '信贷情况']
# 创建一个列表,包含了数据集中每个特征对应的名称,用于后续对数据和决策树的理解和操作
# 返回数据集和分类属性
return dataSet, labels
# 函数执行完毕后,返回创建好的数据集dataSet和对应的分类属性列表labels
#3.splitDataSet函数说明:按照给定特征划分数据集
#Parameters: dataSet:待划分的数据集
# axis:划分数据集的特征
# value:需要返回的特征值
#Returns: 无
def splitDataSet(dataSet, axis, value):
# 创建返回的数据集列表
retDataSet = []
# 创建一个空列表,用于存储划分后符合条件的数据样本,它将作为函数的返回值
# 遍历数据集
for featVec in dataSet:
if featVec[axis] == value:
# 对于数据集中的每个特征向量,检查其在指定的特征索引axis处的值是否等于给定的特征值value,如果相等,则说明该样本符合划分条件,需要进行后续处理
# 去掉axis特征
reduceFeatVec = featVec[:axis]
# 创建一个新的列表,它包含了原特征向量featVec中指定特征索引axis之前的所有元素,即去掉了指定特征
# 将符合条件的添加到返回的数据集
reduceFeatVec.extend(featVec[axis + 1:])
# 将原特征向量featVec中指定特征索引axis之后的所有元素添加到reduceFeatVec中,这样就得到了一个去掉指定特征的新特征向量
retDataSet.append(reduceFeatVec)
# 将处理好的新特征向量reduceFeatVec添加到retDataSet列表中,该列表最终将包含所有符合划分条件的样本
# 返回划分后的数据集
return retDataSet
# 函数执行完毕后,返回划分后的数据集retDataSet
#4.chooseBestFeatureToSplit函数说明:计算给定数据集的经验熵(香农熵)
#Parameters: dataSet:数据集
#Returns: shannonEnt:信息增益最大特征的索引值
def chooseBestFeatureToSplit(dataSet):
# 特征数量
numFeatures = len(dataSet[0]) - 1
# 获取数据集中每个样本的特征数量,通过取数据集中第一个样本的长度并减去1(因为最后一个元素是标签)来得到
# 计数数据集的香农熵
baseEntropy = calcShannonEnt(dataSet)
# 调用calcShannonEnt函数计算数据集的初始香农熵,即未考虑任何特征划分时的熵值,将其作为基础熵值保存起来,用于后续计算信息增益
# 信息增益
bestInfoGain = 0.0
# 初始化信息增益的最大值为0.0,后续将在遍历特征的过程中不断更新这个值,以找到最大的信息增益
# 最优特征的索引值
bestFeature = -1
# 初始化最优特征的索引值为 -1,同样在遍历特征过程中,当找到信息增益最大的特征时,将更新这个值为该特征的实际索引
# 遍历所有特征
for i in range(numFeatures):
# 循环变量i从0到特征数量减1,代表每个特征的索引,开始遍历数据集中的每一个特征
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
# 对于当前遍历到的特征索引i,创建一个列表featList,它包含了数据集中每个样本在该特征索引处的值,即提取了数据集中所有样本的第i个特征的值
# 创建set集合{},元素不可重复
uniqueVals = set(featList)
# 将featList转换为集合uniqueVals,集合中的元素具有唯一性,这样就可以得到该特征所有可能出现的不同值,用于后续根据不同值划分数据集并计算条件熵
# 经验条件熵
newEntropy = 0.0
# 初始化经验条件熵的值为0.0,用于在后续根据不同特征值划分数据集后计算条件熵,并累加到这个变量中
# 计算信息增益
for value in uniqueVals:
# 遍历当前特征的所有不同值,即遍历集合uniqueVals中的每个元素
# subDataSet划分后的子集
subDataSet = splitDataSet(dataSet, i, value)
# 对于当前特征的每个不同值value,调用splitDataSet函数根据该特征值对数据集进行划分,得到划分后的子集subDataSet
# 计算子集的概率
prob = len(subDataSet) / float(len(dataSet))
# 计算划分后得到的子集subDataSet在原数据集中所占的比例,即该子集出现的概率,通过子集的长度除以原数据集的长度来得到
# 根据公式计算经验条件熵
newEntropy += prob * calcShannonEnt((subDataSet)) # 调用calcShannonEnt
# 根据条件熵的计算公式,将子集出现的概率乘以该子集的香农熵(通过调用calcShannonEnt函数计算得到),并累加到newEntropy中,这样就逐步计算出了基于当前特征的经验条件熵
# 信息增益
infoGain = baseEntropy - newEntropy # 计算信息增益
# 根据信息增益的计算公式"信息增益 = 基础熵 - 条件熵",用之前计算得到的基础熵baseEntropy减去当前特征的经验条件熵newEntropy,得到当前特征的信息增益infoGain
# 打印每个特征的信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain))
# 打印出当前特征的信息增益值,方便查看每个特征对分类的贡献程度,格式为"第特征索引个特征的增益为具体增益值",其中具体增益值保留三位小数
# 计算信息增益
if (infoGain > bestInfoGain):
# 检查当前特征的信息增益是否大于之前记录的最大信息增益bestInfoGain,如果大于,则说明找到了一个信息增益更大的特征
# 更新信息增益,找到最大的信息增益
bestInfoGain = infoGain
# 如果当前特征的信息增益更大,就更新最大信息增益的值为当前特征的信息增益值
# 记录信息增益最大的特征的索引值
bestFeature = i
# 同时更新最优特征的索引值为当前特征的索引i,表2024-11-07 0:00:00示当前特征是目前找到的信息增益最大的特征
# 返回信息增益最大特征的索引值
return bestFeature
# 函数执行完毕后,返回信息增益最大特征的索引值bestFeature
#5.createTree函数说明:创建决策树
#Parameters: dataSet:训练数据集
# labels:分类属性标签
# featLabels:存储选择的最优特征标签
#Returns: myTree:决策树
def createTree(dataSet, labels, featLabels):
# 取分类标签(是否放贷:yes or no)
classList = [example[-1] for example in dataSet]
# 创建一个列表classList,它包含了数据集中每个样本的分类标签,通过提取每个样本的最后一个元素得到,用于后续判断数据集中的类别是否完全相同
# 如果类别完全相同,则停止继续划分
if classList.count(classList[0]) == len(classList):
return classList[0]
# 检查classList中第一个元素出现的次数是否等于列表的长度,如果相等,说明数据集中所有样本的分类标签都相同,此时不需要再继续划分数据集创建决策树,直接返回该相同的分类标签即可
# 选择最优特征
bestFeat = chooseBestFeatureToSplit(dataSet)
# 调用chooseBestFeatureToSplit函数,在给定的数据集中选择信息增益最大的特征,并将该特征的索引值赋给bestFeat,这个特征将作为当前划分数据集创建决策树的最优特征
# 最优特征的标签
bestFeatLabel = labels[bestFeat]
# 根据最优特征的索引值bestFeat,从分类属性标签列表labels中获取该最优特征对应的标签,将其赋给bestFeatLabel
featLabels.append(bestFeatLabel)
# 将最优特征的标签添加到featLabels列表中,用于记录在创建决策树过程中已经选择过的最优特征标签
# 根据最优特征的标签生成树
myTree = {bestFeatLabel: {}}
# 根据最优特征的标签创建一个字典myTree,并将其初始化为一个以最优特征标签为键,值为空字典的结构,这个字典将逐步构建成完整的决策树
# 删除已经使用的特征标签
del(labels[bestFeat])
# 从分类属性标签列表labels中删除已经被选为最优特征的那个标签,因为在后续递归创建决策树时,不需要再考虑这个已经使用的特征
# 得到训练集中所有最优特征的属性值
featValues = [example[bestFeat] for example in dataSet]
# 创建一个列表featValues,它包含了数据集中每个样本在最优特征索引处的值,即获取了训练集中所有最优特征的属性值,用于后续根据这些属性值进一步划分数据集并递归创建决策树
# 去掉重复的属性值
uniqueVls = set(featValues)
# 将featValues转换为集合uniqueVls,得到最优特征所有可能出现的不同属性值,集合中的元素具有唯一性,这样可以根据这些不同值分别划分数据集并递归创建决策树
# 遍历特征,创建决策树
for value in uniqueVls:
myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet, bestFeat, value),
labels, featLabels) # 递归调用createTree
# 遍历最优特征的所有不同属性值。对于每个属性值value,首先调用splitDataSet函数根据最优特征和该属性值对数据集进行划分,得到划分后的数据集。然后递归调用createTree函数,使用划分后的数据集、更新后的分类属性标签列表labels和已经记录的最优特征标签列表featLabels继续创建决策树,并将创建好的子决策树作为当前决策树字典myTree中以最优特征标签为键,以该属性值为键的子字典的值
return myTree
# 函数执行完毕后,返回创建好的完整决策树myTree
#6.使用决策树进行分类
#Parameters: inputTree;已经生成的决策树
# #featLabels:存储选择的最优特征标签
#testVec:测试数据列表,顺序对应最优特征标签
#Returns: classLabel:分类结果
def classify(inputTree, featLabels, testVec):
# 获取决策树节点
firstStr = next(iter(inputTree))
# 获取决策树的根节点的键,即决策树字典中的第一个键,通过将决策树字典转换为迭代器并获取下一个元素得到,这个键通常是在创建决策树时选择的第一个最优特征的标签
# 下一个字典
secondDict = inputTree[firstStr]
# 根据根节点的键firstStr,从决策树字典inputTree中获取对应的值,这个值是一个字典,它包含了根据根节点特征的不同取值划分出的子决策树或分类结果等信息
featIndex = featLabels.index(firstStr)
# 根据最优特征的标签firstStr在featLabels列表中的索引,确定测试数据中对应特征的索引位置
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
# 如果当前节点的值是一个字典,说明还需要继续递归向下分类,再次调用classify函数,传入当前子字典、featLabels和测试数据,继续进行分类操作
else: classLabel = secondDict[key]
# 如果当前节点的值不是字典,说明已经到达叶子节点,直接返回该节点的值作为分类结果
return classLabel
# 函数执行完毕后,返回分类结果classLabel
#7.main函数说明:主函数
if __name__ == '__main__':
dataSet, labels = createDataSet()
# 调用createDataSet函数创建数据集和对应的分类属性标签列表
featLabels = []
# 创建一个空的featLabels列表,用于存储在创建决策树过程中选择的最优特征标签
myTree = createTree(dataSet, labels, featLabels) # 生成决策树模型
# 调用createTree函数,使用创建好的数据集、分类属性标签和空的featLabels列表来生成决策树模型,并将生成的决策树赋值给myTree
# 测试数据
testVec = [0, 1]
# 创建一个测试数据列表testVec,用于后续对生成的决策树进行测试分类
result = classify(myTree, featLabels, testVec) # 测试样本
# 调用classify函数,使用生成的决策树、存储最优特征标签的featLabels列表和测试数据testVec对测试样本进行分类,并将分类结果赋值给result
if result == 'yes':
print('放贷')
# 如果分类结果为'yes',则打印出'放贷',表示根据决策树的分类结果,应该进行放贷操作
if result == 'no':
print('不放贷')
# 如果分类结果为'no',则打印出'不放贷',表示根据决策树的分类结果,