深 度 学 习

神经网络基础

一、逻辑回归( Logic Regression )

1 问题的模型

模型：

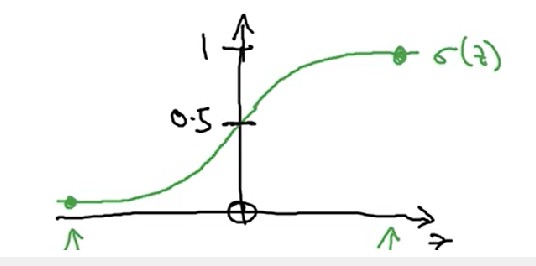
其中xx为输入量，y^y^​预测量，σ()σ()激活函数。   逻辑回归主要用于二分类问题的拟合：0≤y^=P(y=1∣x)≤10≤y^​=P(y=1∣x)≤1，σ(z)σ(z)如图：

​

问题：

对于模型(1.1)(1.1)，需要通过一系列的样本(x,y={0,1})(x,y={0,1})，求解出系数w,bw,b。

求解：

转为最优化问题，然后对未知系数进行求解。

2 最优化问题求解

2.1 损失函数(Loss Function)

1. 作用：   用于衡量单个样本，在进行模型预测后 y 与 y^之间的差距。

2. 二分问题的损失函数

3. 拟合问题的一般损失函数

   L(y,y^)=∣∣y−y^∣∣2L(y,y^)=∣∣y−y^∣∣2

注意：

L()L()函数应该是凸集，防止在寻优的过程中出现多个局部最优解。(y=x2y=x2就是典型的凸集)

2.2 消耗函数(Cost Function)

用于对全部 的样本的预测结果进行评估。也就是最终寻优的目标函数。

J(w,b)=1m∑i=1mL(y(i),y^(i))(2.2)J(w,b)=m1​i=1∑m​L(y(i),y^​(i))(2.2)

2.3 寻优方法

对于目标函数JJ使用梯度下降法进行寻优，迭代更新(w,b)(w,b)，最终得到使得JJ最小的变量值(w,b)(w,b)就是模型(1.1)(1.1)的解。也就完成了对于模型的训练。

{w=w−αdJdwb=b−αdJdb(2.3)⎩⎪⎨⎪⎧​w=w−αdwdJ​b=b−αdbdJ​​(2.3)

二、浅层神经网络(Shallow Neural Network)

2.1 模型结构

BP神经网络层只有三层：Input layer，Hiden layer，Output layer；

​

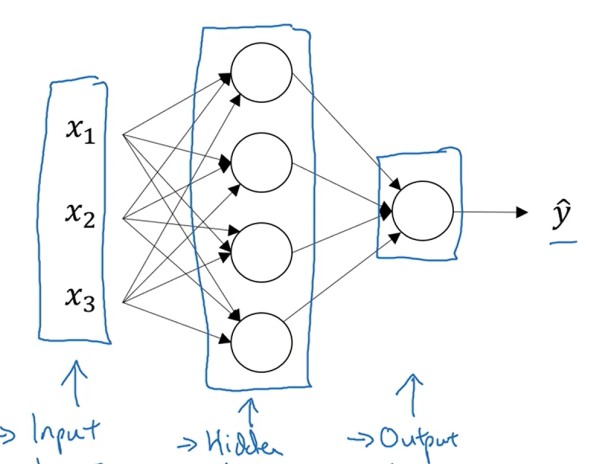
节点的计算与逻辑回归相似。

{z[i]=(w[i])Tx+b[i]a[i]=σ(z[i])(2.4){z[i]=(w[i])Tx+b[i]a[i]=σ(z[i])​(2.4)

2.2 激活函数

1. sigmoid

   二分问题，输出节点必使用sigmoid。
   {a=11+e−zdadz=a(1−a)(2.5){a=1+e−z1dzda=a(1−a)(2.5)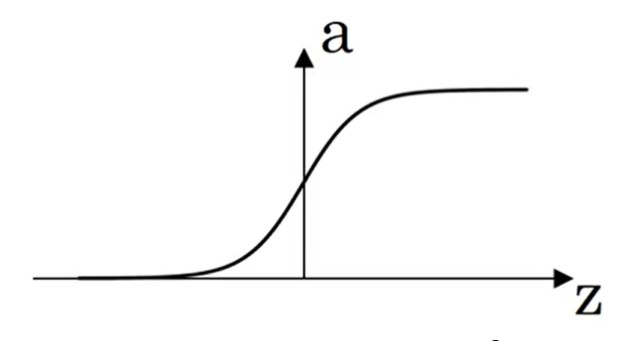

   ​

2. tanh (tansig) MATLAB中的 tansig 激活函数，就是tanh的化解形式。

   {a=ez−e−zez+e−zdadz=1−a2(2.6){a=ez+e−zez−e−zdzda=1−a2(2.6)

   ​

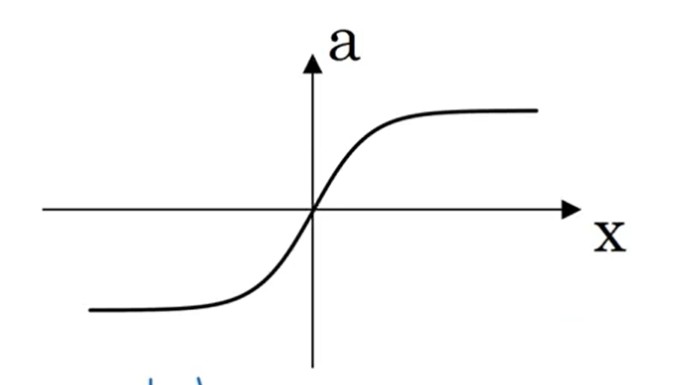
3. ReLU

   拟合问题，输出节点必使用ReLU
   {a=max(0,z)dadz=if(z≥0):1,0(2.7){a=max(0,z)dzda=if(z≥0):1,0(2.7)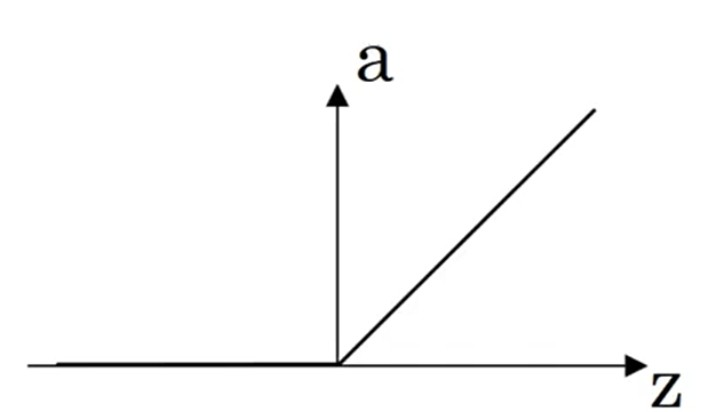

   ​

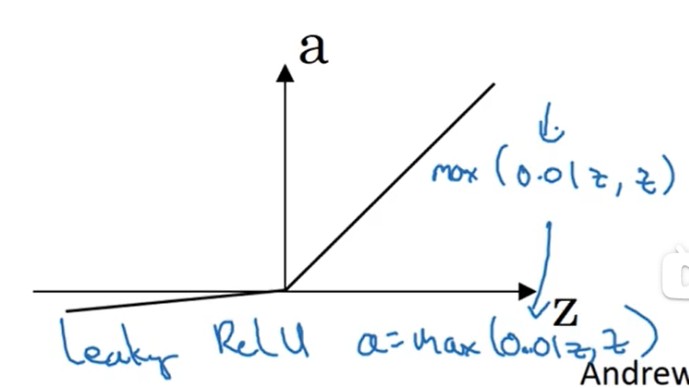
4. Leaking ReLU

   {a=max(0.01z,z)dadz=if(z≥0):1,0.01(2.7){a=max(0.01z,z)dzda=if(z≥0):1,0.01(2.7)

   ​

2.3 正向传播(frontpropagation)与反向传播(backpropagation)

1. 正向传播

   ​

2. 反向传播

   dz[2]=a[2]−ydW[2]=dz[2]a[1]Tdb[2]=dz[2]dz[1]=W[2]Tdz[2]∗g[1]′(z[1])dW[1]=dz[1]xTdb[1]=dz[1](2.8)dz[2]=a[2]−ydW[2]=dz[2]a[1]Tdb[2]=dz[2]dz[1]=W[2]Tdz[2]∗g[1]′(z[1])dW[1]=dz[1]xTdb[1]=dz[1](2.8)

注意：

• 代表的是：numpy.multiply()
• 上述反向传播公式只适用于二分问题

2.4 w系数初始化

• 隐含层节点的初始化值应当不同；否则会导致节点的计算结果一样，多节点无意义。
• W的初始化值应当较小；使得激活函数落在斜率大的地方，梯度下降法收敛快

改善深层神经网络

一、基础理论

1.1 超参数

对于神经网络模型而言，决定最终神经网络模型性能的系数是w和b，其余可调的系数均为超参数。

1.2 训练集、测试集和开发集

在模型生成的过程中，根据样本数据起到的作用，进行集合类型的划分。

• 训练集(Train Set): 用于模型的训练。
• 开发集(Dev Set): 用于对训练中的模型进行测试。
• 测试集(Test Set): 用于对最终的模型进行测试。

注意：训练集和开发集的数据应当来自于同一组样本。

1.3 方差(Variance)和偏差(Bias)

1. 偏差

   模型在样本上，输入与输出之间的误差，即模型本身的精确度。反应在训练集上。

2. 方差

   模型预测结果与输出期望之间的误差，即模型的稳定性。反应在开发集与训练集上。

3. 关系

   • 低偏差|低方差：最想要的结果。
   • 低偏差|高方差： 过拟合 (overfitting) ，对测试集和开发集拟合能力差。
   • 高偏差： 欠拟合 (underfitting) ，模型拟合得很差。

1.4 过拟合与欠拟合解决方案

• 过拟合

  • 简化模型复杂度
  • L2正则化和Dropout
  • 增加样本数量

• 欠拟合

  • 使用更复杂的神经网络模型
  • 更换优化方法
  • 增加迭代训练次数

二、正则化（regularization）

作用：降低模型的复杂度，从而防止模型的过拟合问题。

2.1 L2正则化

在梯度下降法中，对于目标函数J添加一个正则项：

J(w,b)=1m∑i=1mL(y(i),y^(i))+λ2m∑l∣∣w[l]∣∣22(2.1)J(w,b)=m1​i=1∑m​L(y(i),y^​(i))+2mλ​l∑​∣∣w[l]∣∣22​(2.1)

这就会导致更新每一层的w系数时：

wL2[l]=w[l]−α(dw[l]+λmw[l])(2.2)wL2[l]​=w[l]−α(dw[l]+mλ​w[l])(2.2)

增大系数λλ便会使得w[l]w[l]的值减小；当一个神经元节点的w≈0w≈0时，该神经元节点便在模型中失效。

​

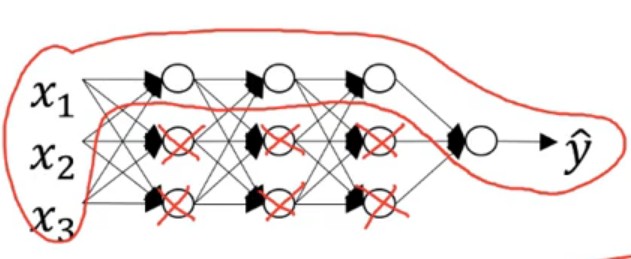
2.2 Droput正则

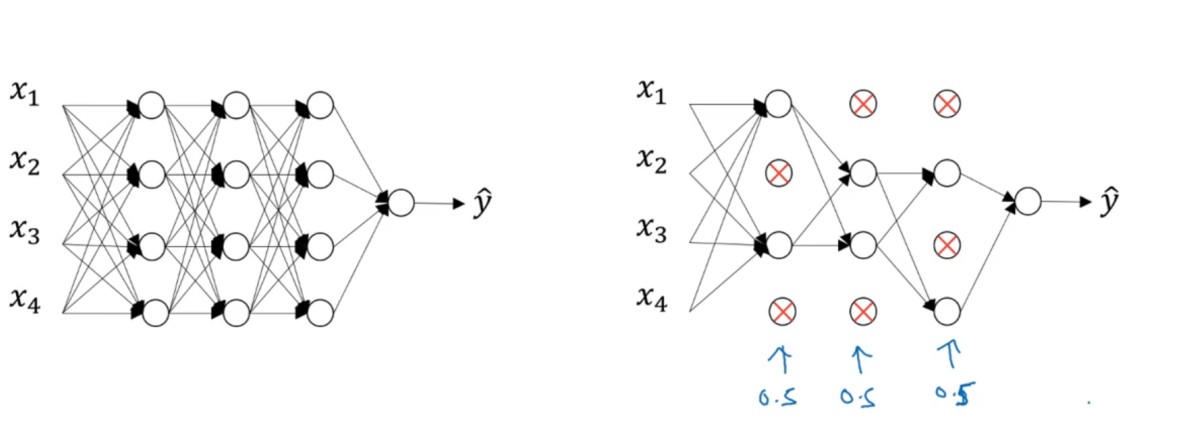
减少一次训练样本中的节点，防止过拟合。不依赖一个特性，将权重值分散。

​

• 实现：将a[l]a[l]中的某些元素置为0。(inverted dropout)

• 注意：

  • 经过处理后的J无明确的意义
  • 该方法主要用于图像识别

三、归一化(Normalize)

对于样本首先进行归一化处理，然后才能使用。

3.1 映射到[-1,1]

正向：

Xnorm=2Xmax−Xmin(X−Xmin)−1(3.1)Xnorm​=Xmax​−Xmin​2​(X−Xmin​)−1(3.1)

反向：

X=(Xnorm+1)Xmax−Xmin2+Xmin(3.2)X=(Xnorm​+1)2Xmax​−Xmin​​+Xmin​(3.2)

3.2 映射到[0,1]

正向：

Xnorm=X−XminXmax−XminXnorm​=Xmax​−Xmin​X−Xmin​​

反向：

X=Xnorm(Xmax−Xmin)+Xmin(3.2)X=Xnorm​(Xmax​−Xmin​)+Xmin​(3.2)

四、系数初始化

4.1 梯度消失与梯度爆炸

​

假设一个深层的网络，其激活函数为线性的，且网络中的偏执系数 b[l]=0b[l]=0

y^=w[L]w[L−1]⋯w[1]Xy^​=w[L]w[L−1]⋯w[1]X

则

a[l]=w[l]w[l−1]⋯w[1]Xa[l]=w[l]w[l−1]⋯w[1]X

进一步假设 w[l]=Ww[l]=W 都相等

a[l]=WlXa[l]=WlX

令上图网络中的 W=[1.2001.2]W=[1.20​01.2​] 则

a[l]=[1.2l001.2l]Xa[l]=[1.2l0​01.2l​]X

随着网络的加深，就会导致 a[l]a[l] 指数爆炸。

令上图网络中的 W=[0.9000.9]W=[0.90​00.9​] 则

a[l]=[0.9l000.9l]Xa[l]=[0.9l0​00.9l​]X

随着网络的加深，就会导致 a[l]a[l] 会趋近于 0。

根据梯度求导公式

dw[l]=dz[l]a[l−1]dw[l]=dz[l]a[l−1]

综上可得

• 当前l-1 个的系数矩阵 WW 中的分量 wij<1wij<1 ，会导致 a[l−1]a[l−1] 趋近于零，进而使得 dw[l]≈0dw[l]≈0，即「梯度消失」
• 当前l-1 个的系数矩阵 WW 中的分量 wij>1wij>1 ，会导致 a[l−1]a[l−1] 指数爆照，进而使得 dw[l]dw[l] 指数爆炸 ，即「梯度爆炸」

4.2 初始值选取

对于深度的神经网络；

• 当w > 1时，从输入层到输出层，输出值将会很大
• 当w < 1时，从输入层到输出层，输出值将会很小

为了避免这些问题，需要对w值进行合理的初始化。即 var(w[l])=2n[l],E(w[l])=0var(w[l])=n[l]2​,E(w[l])=0

w[l]=numpy.multiply(randn(),2n[l])(4.1)w[l]=numpy.multiply(randn(),n[l]2​​)(4.1)

其中nn代表一个神经元节点输入的个数。

五、指数加权平均

vt=βvt−1+(1−β)θt(5.1)vt​=βvt−1​+(1−β)θt​(5.1)

对于vtvt​可以认为是前11−β1−β1​个v值的平均值。

在初始时刻，使用指数加权平均，会导致估计值偏差较大。在后期时刻，偏差就基本近似。所以可以对初期的估计值进行修正。

vt=vt1−βt(5.2)vt​=1−βtvt​​(5.2)

六、Mini Batch

6.1 模型

将样本数据中的训练集再划分为多个子集，再依次利用这些子集进行模型训练。

• 子集的样本量：m≤200m≤200
• 子集的个数：2i2i
• mini batch 训练过程中，J的变化是振荡。

​

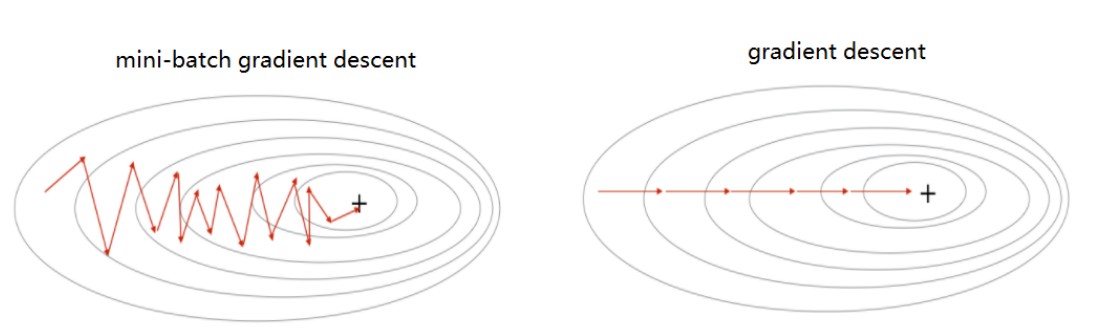
6.2 梯度下降法

对于梯度下降法，Mini Batch的(w,b) 的变化如上图所示，是振荡的，向着最优解靠近。在这种情形下，使用梯度下降法时，学习率αα不能太大。

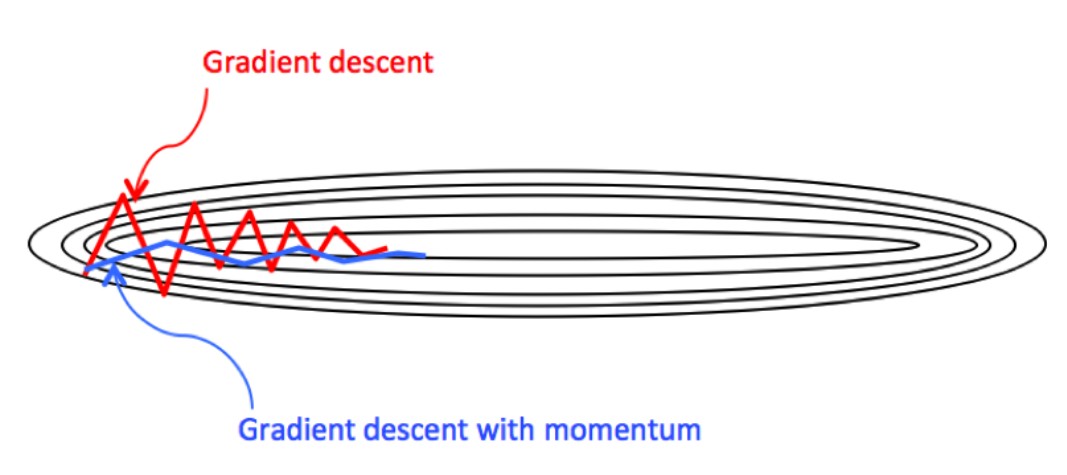
6.3 动量梯度下降法

对变量（w,b）使用 指数加权平均 降低振荡，使得收敛过程更加的平缓。这样就能加大学习率αα，减少迭代次数。

vdw=βvdw+(1−β)dwvdb=βvdb+(1−β)dbw=w−αvdw,b=b−αvdb(6.1)vdw​=βvdw​+(1−β)dwvdb​=βvdb​+(1−β)dbw=w−αvdw​,b=b−αvdb​​(6.1)

​

6.4 RMSprop法

在降低振荡振幅的基础上，还要缩短纵轴的波动，延长横轴的长度。

Sdw=βSdw+(1−β)(dw.∗dw)Sdb=βSdb+(1−β)(db.∗db)w=w−αdwSdw+ϵb=b−αdwSdb+ϵ(6.2)Sdw​Sdb​wb​=βSdw​+(1−β)(dw.∗dw)=βSdb​+(1−β)(db.∗db)=w−αSdw​+ϵ​dw​=b−αSdb​+ϵ​dw​​(6.2)

其中ϵϵ是一个很小的值，防止SS为0，造成运算异常。

6.5 ADAM法

对RMSprop法和动量法的整合，改进。

vdw=β1vdw+(1−β1)dwvdb=β1vdb+(1−β1)dbSdw=β2Sdw+(1−β2)(dw.∗dw)Sdb=β2Sdb+(1−β2)(db.∗db)vdwcorre=vdw1−β1tvdbcorre=vdb1−β1tSdwcorre=Sdw1−β2tSdbcorre=Sdb1−β2tw=w−αvdwcorreSdwcorre+ϵb=b−αvdbcorreSdbcorre+ϵβ1=0.9β2=0.999(6.3)vdw​vdb​Sdw​Sdb​vdwcorre​vdbcorre​Sdwcorre​Sdbcorre​wbβ1​β2​​=β1​vdw​+(1−β1​)dw=β1​vdb​+(1−β1​)db=β2​Sdw​+(1−β2​)(dw.∗dw)=β2​Sdb​+(1−β2​)(db.∗db)=1−β1t​vdw​​=1−β1t​vdb​​=1−β2t​Sdw​​=1−β2t​Sdb​​=w−αSdwcorre​+ϵ​vdwcorre​​=b−αSdbcorre​+ϵ​vdbcorre​​=0.9=0.999​(6.3)

七、衰减学习率

在训练的前期使用较大的学习率，在快要收敛时，使用较小的学习率。

α=11+delayRate∗epochNumα0(7.1)α=1+delayRate∗epochNum1​α0​(7.1)

八，超参数取值

• 采用枚举法，在一个区间内随机试；

• 对数标尺随机数的实现   从[0.001,1]之间的对数标尺随机数的实现：

  |-----|----------------------------|
  | 1 | r = -4 * np.randm.rand() |
  | 2 | a = 10 ** r |

  Copy to clipboardErrorCopied

九，Batch Norm

9.1 原理

对一个batch样本在一个神经元节点中的所有zj[i]zj[i]​进行Z标准化处理，然后再带入激活函数，求解aj[i]aj[i]​。

​

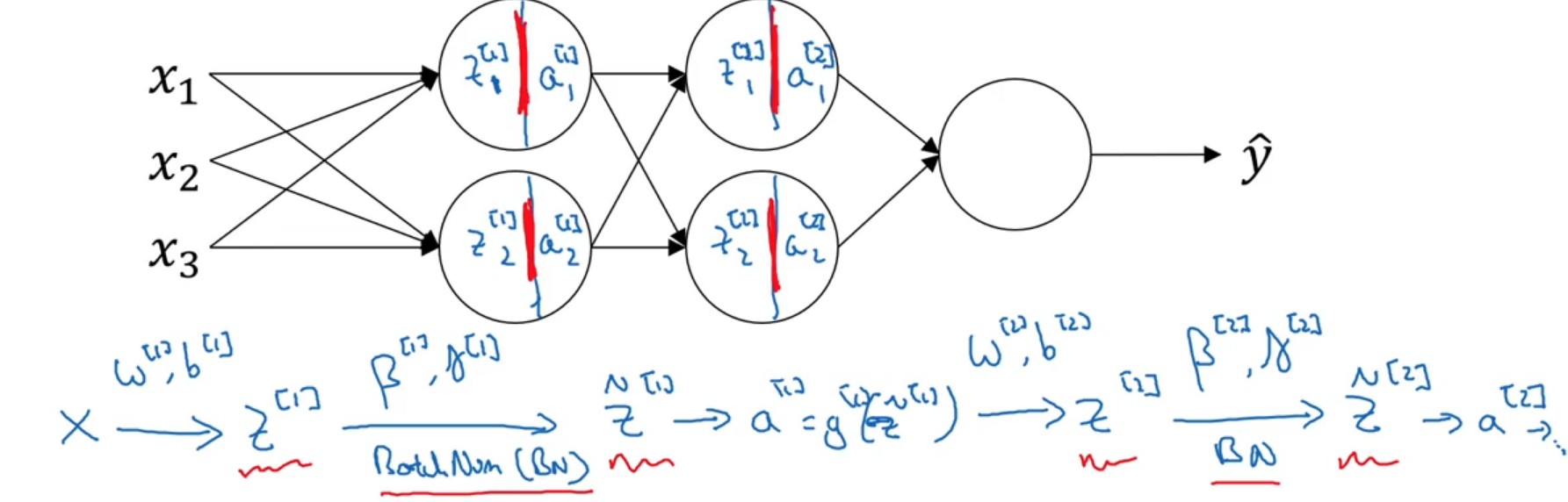
{μ=1m∑iz(i),δ2=1m∑i(z(i)−μ)2znorm(i)=z(i)−μδ2+ϵz^(i)=γznorm(i)+β(9.1)⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧​μznorm(i)​z^(i)​=m1​i∑​z(i),δ2=m1​i∑​(z(i)−μ)2=δ2+ϵ​z(i)−μ​=γznorm(i)​+β​(9.1)

注意：

1. 由于对z(i)z(i)进行了标准化处理，对于系数b[i]b[i]将没有实质意义，可以从网络中去掉；
2. 引入两个调节参数β[i],γ[i]β[i],γ[i]。

9.2 μ,δ的获取

1. 训练集：直接使用min-batch中的所有样本进行计算从而获取。
2. 测试集：将训练集中计算得到的 μ{i},δ{i}μ{i},δ{i}进行指数平均获取到的μ,δμ,δ用于测试计算。

9.3 covariate shift

​

​

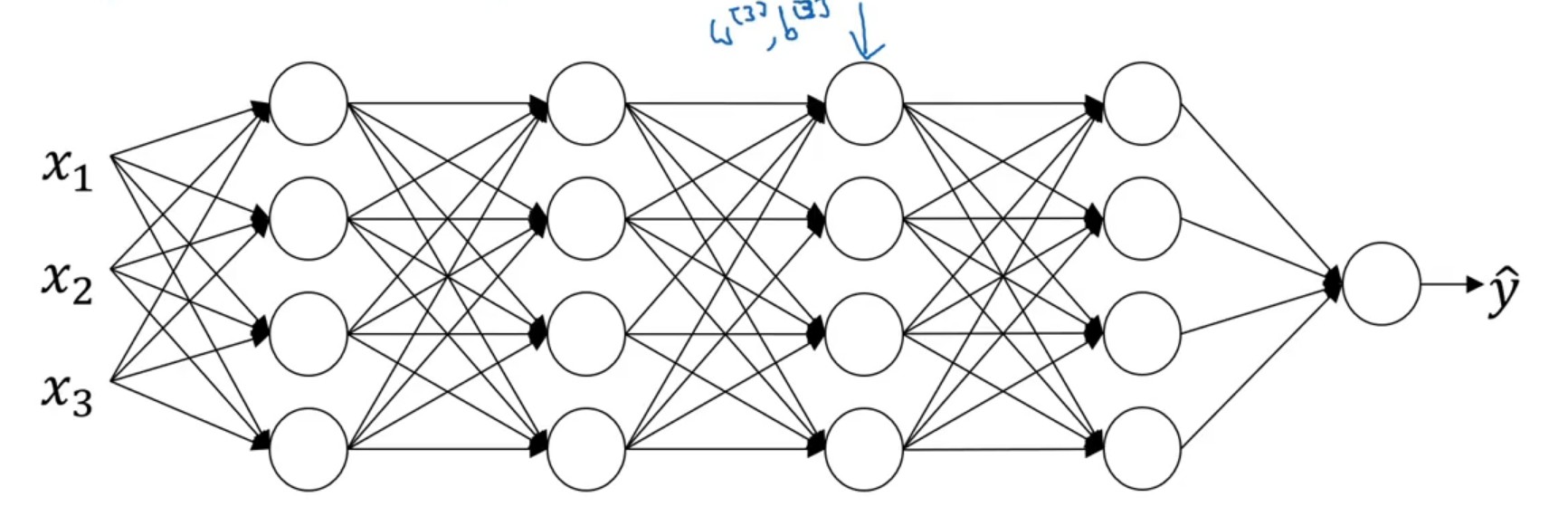
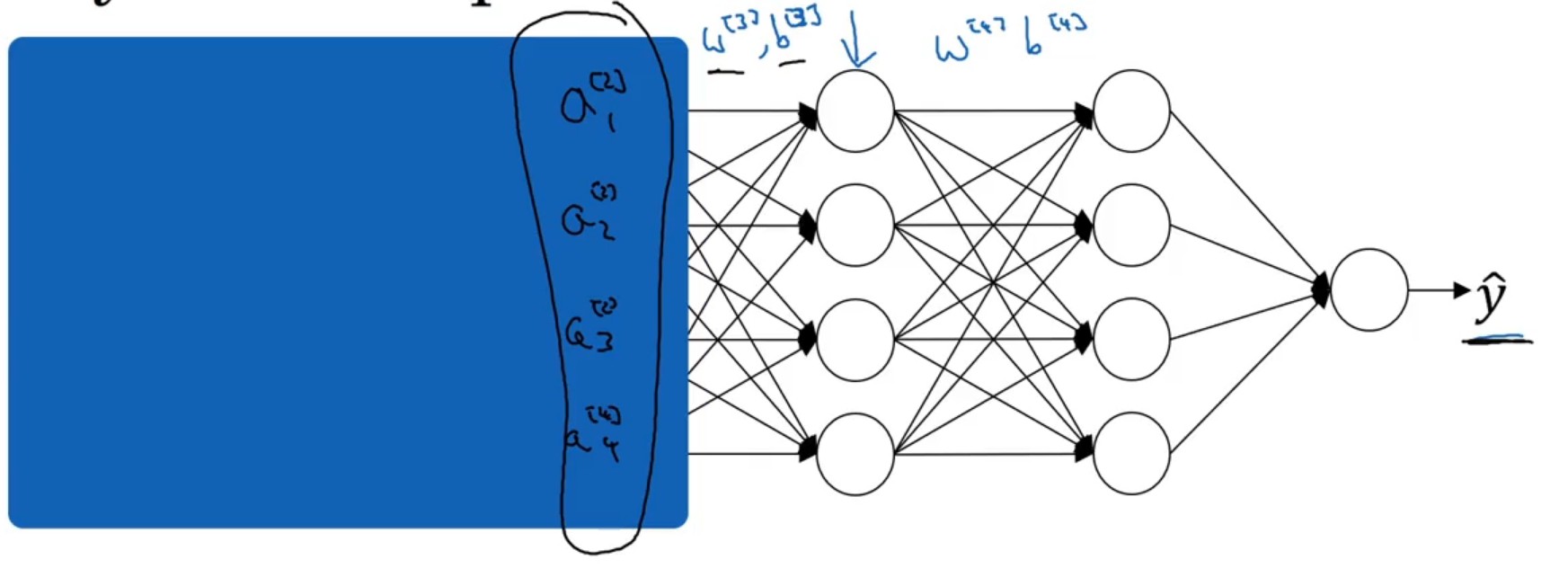
对于第3，4层神经网络而言，它们以a[2]a[2]作为样本输入（就认为是样本定值），从而实现结果向y^y^​靠拢。但是从整体网络上来看a[2]a[2]受到了第1，2层网络的影响，是变化的。因此，对于a[2]a[2]就存在协变量偏移 的情况。Batch Norm的作用就是将每一个神经元激活前的样本尽可能都保持在统一的一个分布内。

十、softmax回归

10.1 作用

可以对种数据类型的学习，实现多类型划分。

10.2 原理

1. 激活函数

   ​

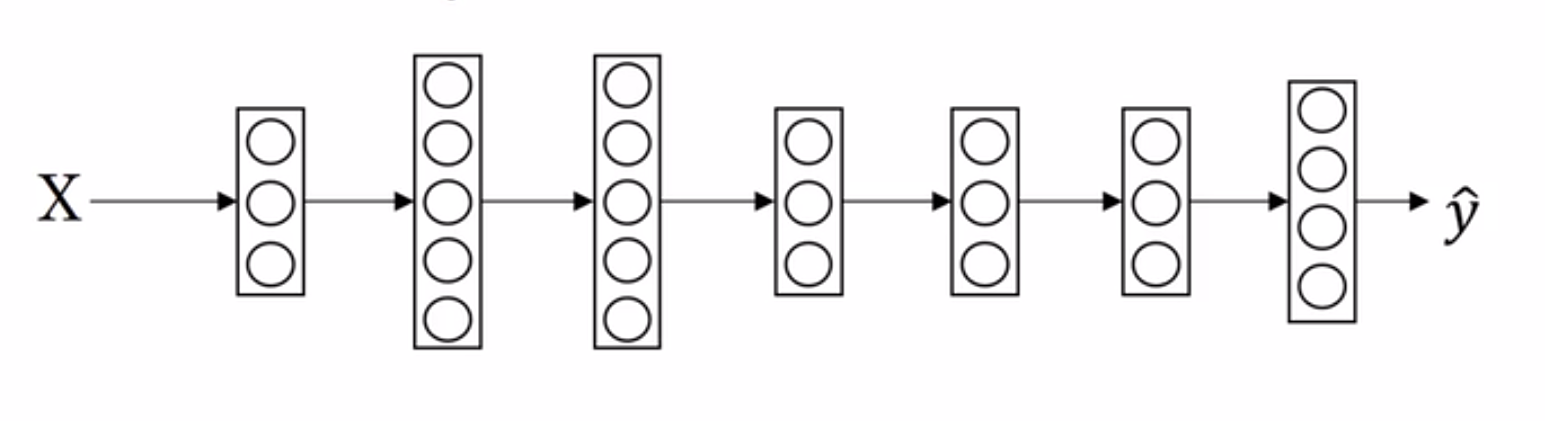
   输出层的节点数量=类别的数量，并且输出层的激活函数为softmax激活函数。
   {z[L]=w[L]a[L−1]+b[L]t=ez[L]y^=[ti∑ti](10.1)⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧z[L]ty^=w[L]a[L−1]+b[L]=ez[L]=[∑titi](10.1)

   其中：   y^y^​各个输出量的总和为1。输出结果就是样本在各个分类所占的概率。

2. 损失函数

   L(y^,y)=−∑iCyilog⁡y^i(10.2)L(y^,y)=−i∑Cyilogy^i(10.2)

3. 目标函数

   J=1m∑imL(y^(i),y(i))(10.3)J=m1i∑mL(y^(i),y(i))(10.3)

10.3 输出(y)编码

1. 顺序编码 对于结果按照数字顺序分类。

   [ABCD][1234][ABCD][1234]

2. one-hot 编码

   A=[1000]B=[0100]C=[0010]D=[0001]A=[1000]B=[0100]C=[0010]D=[0001]

结构化机器学习策略

一、正交化（orthogonalization）

正交化：每次调整的选项最好只影响一个阶段，尽量不要影响其他阶段。

对于模型训练遇到的问题可以分四个阶段：

1. 首先，确保训练集的结果能达到human-level
   • 扩大模型的规模
   • 更换训练方法
2. 其次，开发集的结果能够让人接收
   • 添加正则
   • 增加训练数据量
3. 然后，测试集的结果能达到目标
   • 更大的训练数据量
4. 最后，模型正式使用没问题
   • 修改cost Function
   • 修改指标

二、评价指标

评价指标是在对模型各个阶段的结果进行评价，不是cost function。

2.1 单一评价指标

评价结果好坏的标准应当体现在最终的一个值上（多个评价指标也要规划成一个指标），方便人做出判断，避免选择综合症。

1. F1 分数（调和评价）

   查全率（recall）：分辨出的猫的数量 / 猫的总量 查准率（precision）：分类正确的量 / 总的样本量
   F1=21P+1R(2.1)F1=P1+R12(2.1)

2. 加权平均

2.2 满足和优化指标

当单一评价指标不能对训练目标进行很好描述时，可以使用 满足（satisfacting metrics）+ 优化（optimizing metrics） 。 将所有涉及的指标描述成一个带约束的优化问题，这样就又能形成一个单一的指标。

• optimizing metrics : 主要优化的目标。
• satisfacing metrics : 其余指标的约束条件。

2.3 什么时候应当调整指标

当前的模型指标产生的结果，偏离了或者不满足正式使用的需求，就得马上更改。

三、Human-level

3.1 自然感知问题（natural perception problem）

自然感知类问题：就是人类能根据自身经验做出判断的问题。例如：图像识别，语言识别，给人看病。。。

​

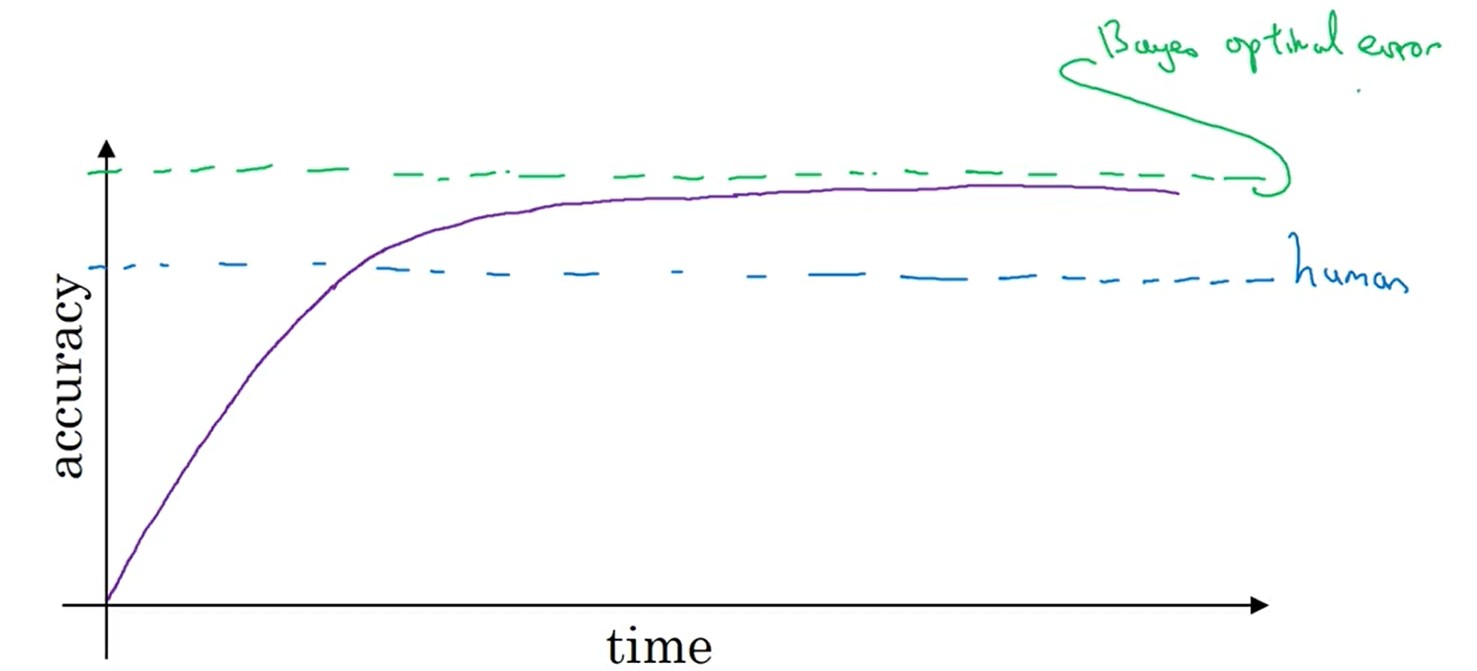
1. 在人类的水平（human-level）以下，精度上升很快，当超过人类水平，速度缓慢，逐渐收敛
2. 理论上模型能达到的最高精度称之为 贝叶斯最优估计（Bayes optimal error）
3. 对于自然感知类问题，人类水平基本上靠近贝叶斯估计，也会直接用人类水平代替贝叶斯估计。
4. 对于模型指标低于人类水平，上面所述的方法有效；当超过人类水平，上面所述的方法可能就效果不明显了。

3.1.1 可避免偏差(avoidable Bias)

​

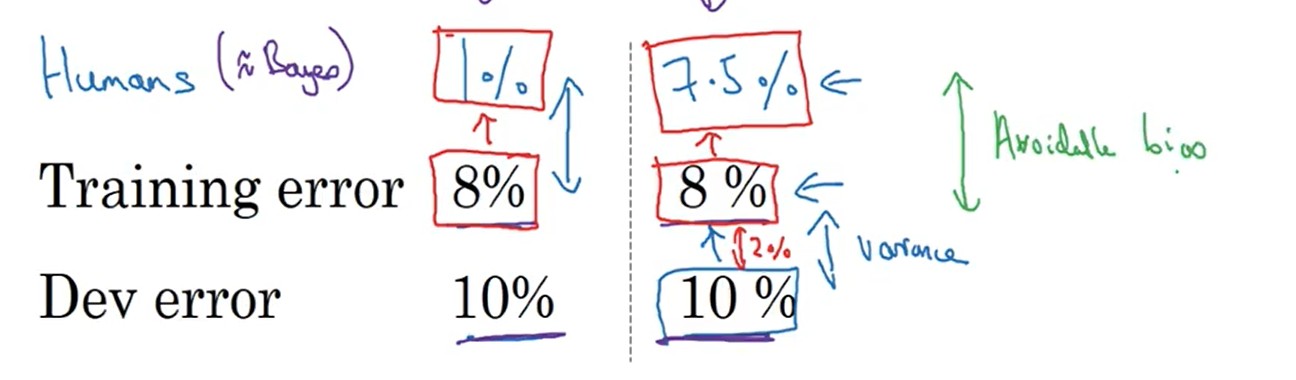
以human-level为基准，来进行偏差和方差分析（分析方法同上一章），然后在采用不同的方法来优化模型训练。

avoidableBias=trainingerror−human−level(3.1)avoidableBias=trainingerror−human−level(3.1)variance=deverror−trainingerror(3.2)variance=deverror−trainingerror(3.2)

3.1.2 human-level取值

human-level的取值应当根据具体的问题要求进行选择。

3.2 超人类水平问题（surpassses human-level）

超人类水平问题：模型的表现远远超过超人类水平的问题，例如广告分析，由A到B汽车行驶时间等等。 对于这些问题的表现超出人的表现，主要是因为模型训练涉及到了大量数据的处理。对于这些问题以人类水平作为基础的模型训练方案就不再适用了。

四、错误分析

​

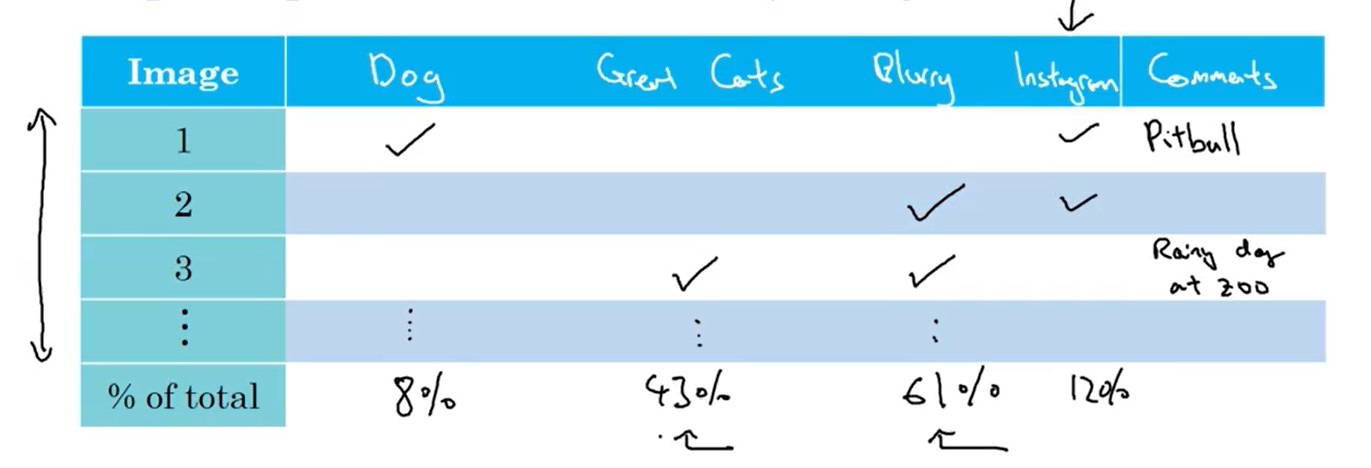
当发现开发集，训练集的指标结果很差劲，可以对 开发集识别错误的样本进行人工分析。

1. 将所有猜想的导致错误的原因 列向标出；所有 错误的样本 在横向列出
2. 人工逐列分析各个样本错误的原因，并统计
3. 最后分析结果，确定优化的方向。

五、样本的结论存在问题

5.1 问题分析

对于收集的样本，如果只是一小部分输入x与输入y之间的对应关系存在问题：

训练集：一般不用修改这些错误，因为训练集样本量大，且算法具有鲁棒性。 开发集：首先进行 错误分析 ，问题样本导致的误差挺大的，就要修正开发集。

5.2 问题修正

当发现问题很严重时，需要就行样本修正：

• 修正后，保证开发集和测试集的分布一致性。
• 也要尽量去检验那些 侥幸计算对的样本
• 修复了开发集和测试集，可能导致与训练集的分布不统一

六、训练的起步

• 先搭建一个简单的模型，不用想太多

• 进行样本错误分析与各个集的误差分析，确定模型优化方向

七、训练集与开发集，测试集分布不同

7.1 实践样本太少的样本划分

当模型实际应用的样本太少或者不好获取时，对于样本的分布就不能在采用训练集，开发集，测试集样本均匀分布的方案，应当将实践样本全划分到开发集和测试集，让模型训练是朝着期望走。

7.2 数据不匹配判别及处理

数据不匹配问题：由于开发集，测试集同训练集的分布不同，可能会导致训练的模型不能达到我们的预期。 为了观测出 是不是由于这问题导致了模型的不准确 又引入了一个 训练-开发集：该集合的样本分布与训练集相同。

​

当 dev error 相对于 train-dev error 比较大时，就存在数据不匹配问题。

• 对比训练集样本与实际样本之间的差别
• 增加实际情况的样本数据
• 人工制造实际情况样本数据，尽量增加数据的多样性（可能会导致对单一情况的过拟合）

八、迁移学习

​

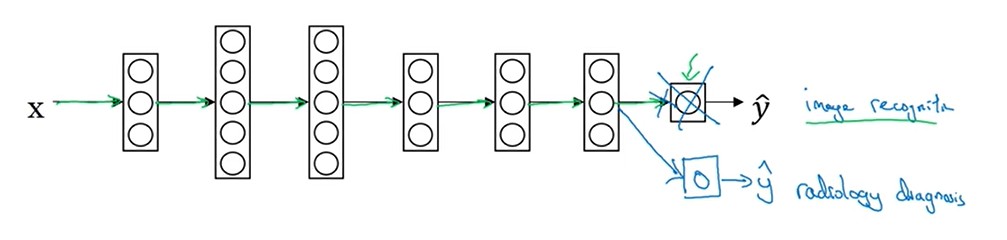
迁移学习：继承其他已经成功的模型，来继续训练当前的模型。

• A模型的x与B模型的x相同
• A模型训练的样本量 相对于 B模型的样本量大的多。
• A模型最开始的几层网络能提升B模型性能的可能性最大：模型从后向前进行修改。

九、多任务学习

多任务学习：将多个训练目的全放到一个模型中进行训练。 对于无人驾驶而言，可以把识别人，车，路标等功能都集成到一个模型中进行训练。

• 多个任务可以共用一套浅层的网络
• 多个任务分开时，样本量应当能保证大体一致，数量平均
• 当效果不好时，主要因素是网络结构太小
• softmax: 分辨的是什么。多任务学习：分辨的是有什么

十、端对端学习

​

直接使用x映射到y，进行神经网络学习，中间不做任何的内容处理，完全的黑箱。

• 好处：

  1. 模型完全依赖数据
  2. 在x -> y的过程中，不用再考虑添加其他处理流程。

• 坏处：

  1. 一般需要大量的数据才能出效果
  2. 人工控制降低

卷积神经网络

一、卷积

1.1 数学运算

​

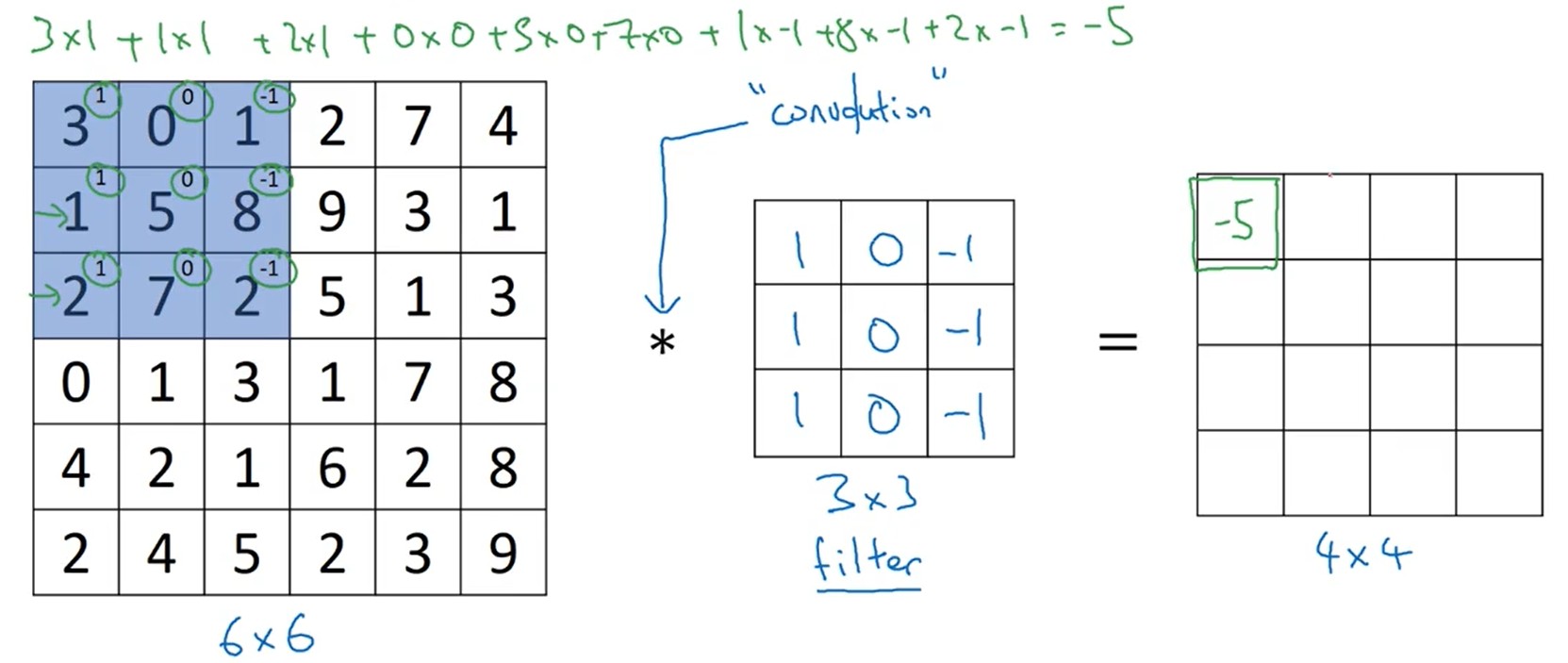
• 单步卷积：计算流程如上图所示，卷积核（过滤器）与图片颜色通道值对应相乘，然后乘积结果再相加。e=H∗A=[h11 h12 h13 h21 h22 h23 h31 h32 h33]∗[abcdefghi]=sum⁡([a×h11 b×h12c×h13 d×h21e×h22f×h23 g×h31 h×h32i×h33])e=H∗A=⎣⎢⎡h11 h21 h31 h12 h22 h32 h13 h23 h33⎦⎥⎤∗⎣⎢⎡adgbehcfi⎦⎥⎤=sum⎝⎜⎛⎣⎢⎡a×h11 d×h21 g×h31 b×h12e×h22 h×h32c×h13f×h23i×h33⎦⎥⎤⎠⎟⎞
• 卷积移动 ：如动态图所示，输入为 7x7 ，卷积核3x3，卷积核移动步长1，输出结果为5x5

​

• 输出维度 ：no=⌊ni+2p−fs+1⌋no=⌊sni+2p−f+1⌋
  • f : 过滤器的纬度
  • p : 输入图片填充的像素
  • s : 过滤器在输入图像上移动的步长

当步长s不为1时，可能导致过滤器越界，所以使用floor进行向下取整。

Tip

在图像识别中所说的"卷积"和实际定义有一点小差别，图像识别省略了：对过滤器进行右对角线的翻转（对结果没啥影响，没必要算了）。图像识别中的卷积准确应当称之为：cross-correlation。

1.2 Padding

​

卷积计算后，原来的图像会被缩小，为了规避这个问题，可以将原来的图像的进行边缘扩充像素。卷积核的步长一般取s=1，那么上面的式就变为

no=ni+2p−f+1no​=ni​+2p−f+1

现在要使得 no=nino​=ni​，可以求解得

p=f−12p=2f−1​

因此，只要再对原图扩充p个像素，就能使得卷积后的图像尺寸和输入图像一样大。例如对5x5的输入，卷积核取3x3，步长为1，当取p=1时，输出结果与原图尺寸一样。

Note

从上面公式可以看出，当卷积步长为1且卷积核的尺寸f 为奇数时，计算得到的p值为整数。因此，一般会选用「奇数」尺寸的卷积核。例如3x3、5x5、7x7等。

二、卷积操作

2.1 边缘监测

​

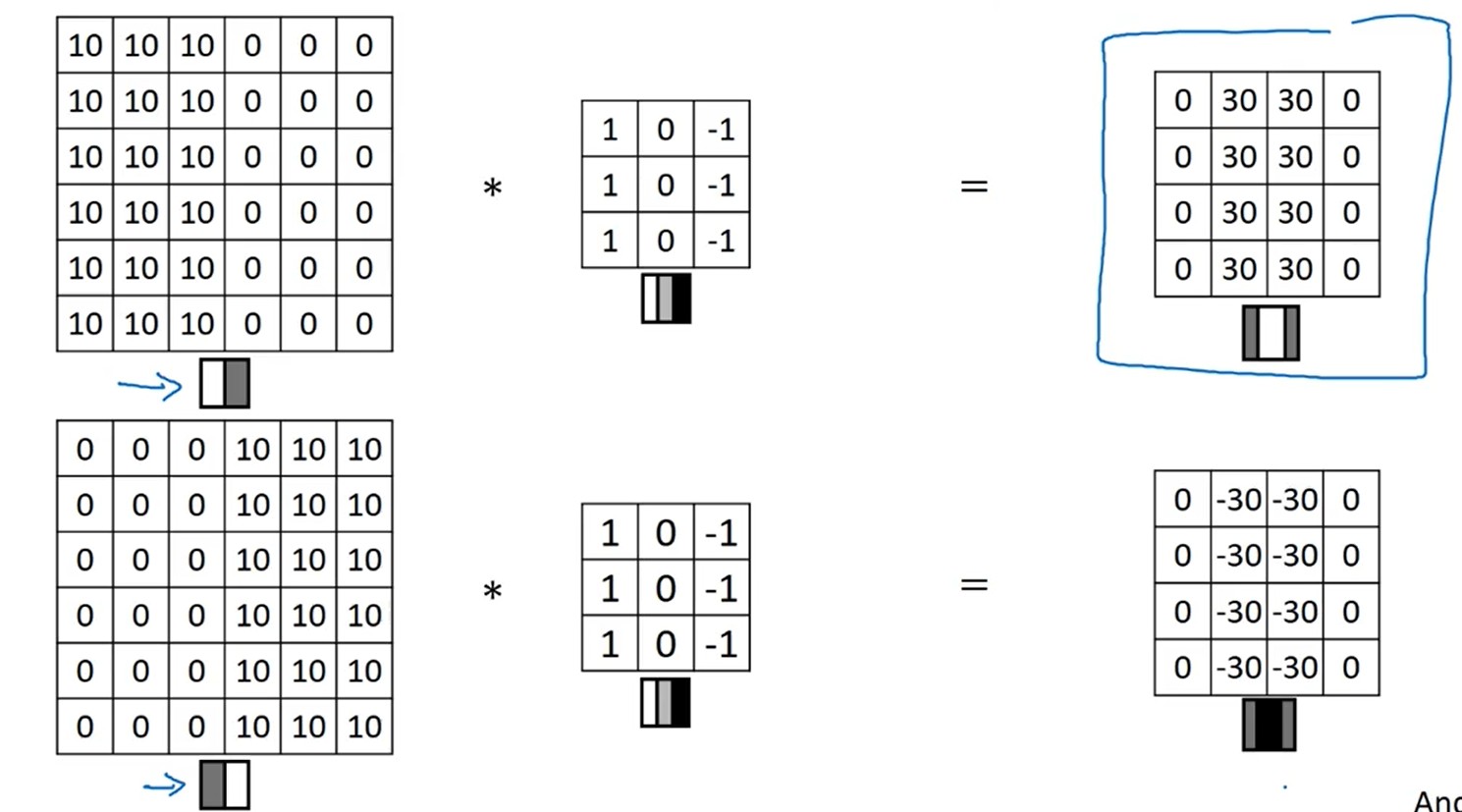
定义一个竖向的过滤器，就能实现对竖向的边缘进行监测；同样定义一个横向的过滤器，就能对一个横向的边缘进行监测。对于过滤器的值，可以自定义，不用完全是-1或者1。

​

2.2 其他卷积操作

三、卷积神经网络

3.1 卷积层

1 卷积核

Note

从上一节可以知道，对图片进行「卷积操作」后，可以对「图像特征」进行提取。因此，卷积神经网络就直接将卷积核中的所有系数都设置为w系数，然后通过训练得到具体的卷积核。

2 三维卷积

​

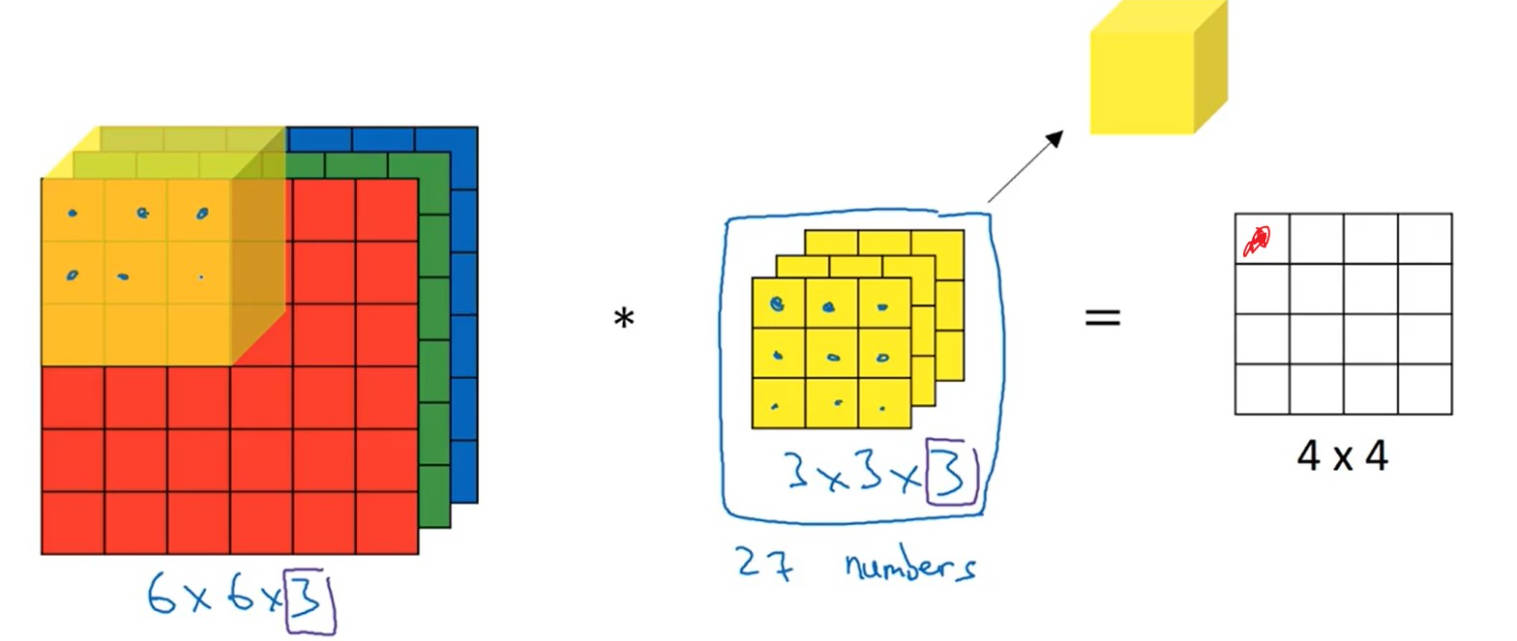
• 输入的通道数和过滤器的通道数相同，才能进行计算。
• 所有颜色通道进行一步卷积计算后，得到一个输出结果，即颜色通道被降维。

3 卷积层结构

​

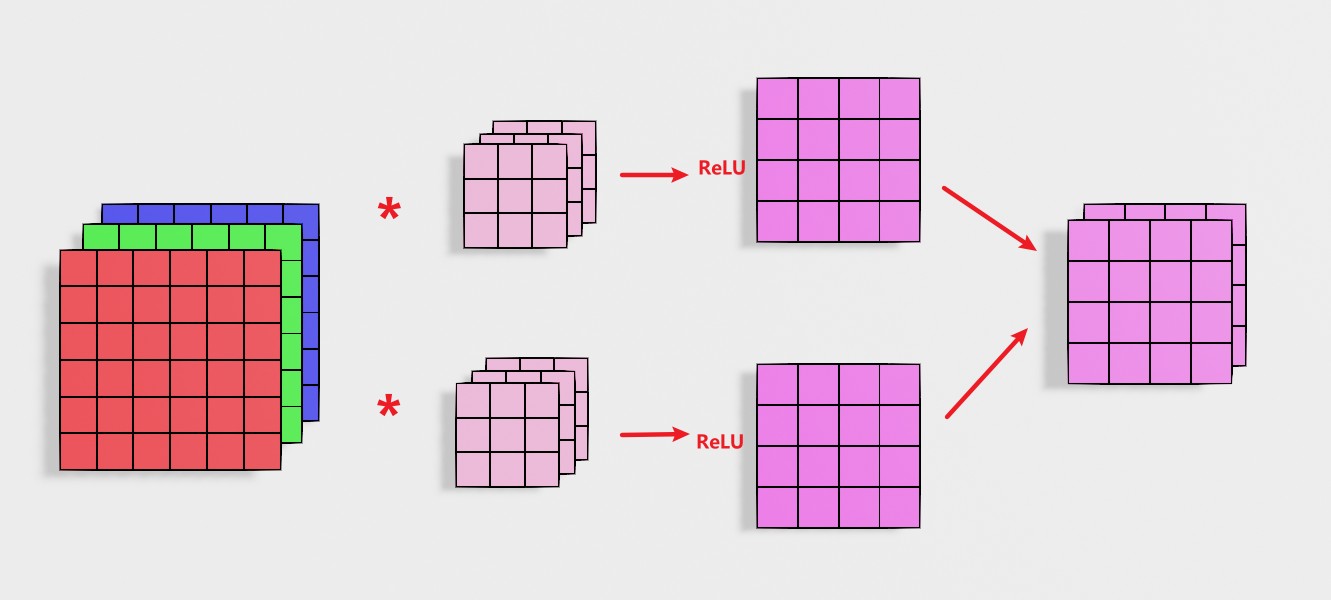
图中展示的卷积层：一张图像通过两个滤波器，计算得到两层结果；再将两层送入激活函数；最后将两个层重合得到输出。这里的卷积核可以设置多个。

a[l]=active(input∗filter+bias)(5.1)a[l]=active(input∗filter+bias)(5.1)

3.2 池化层（pooling）

​

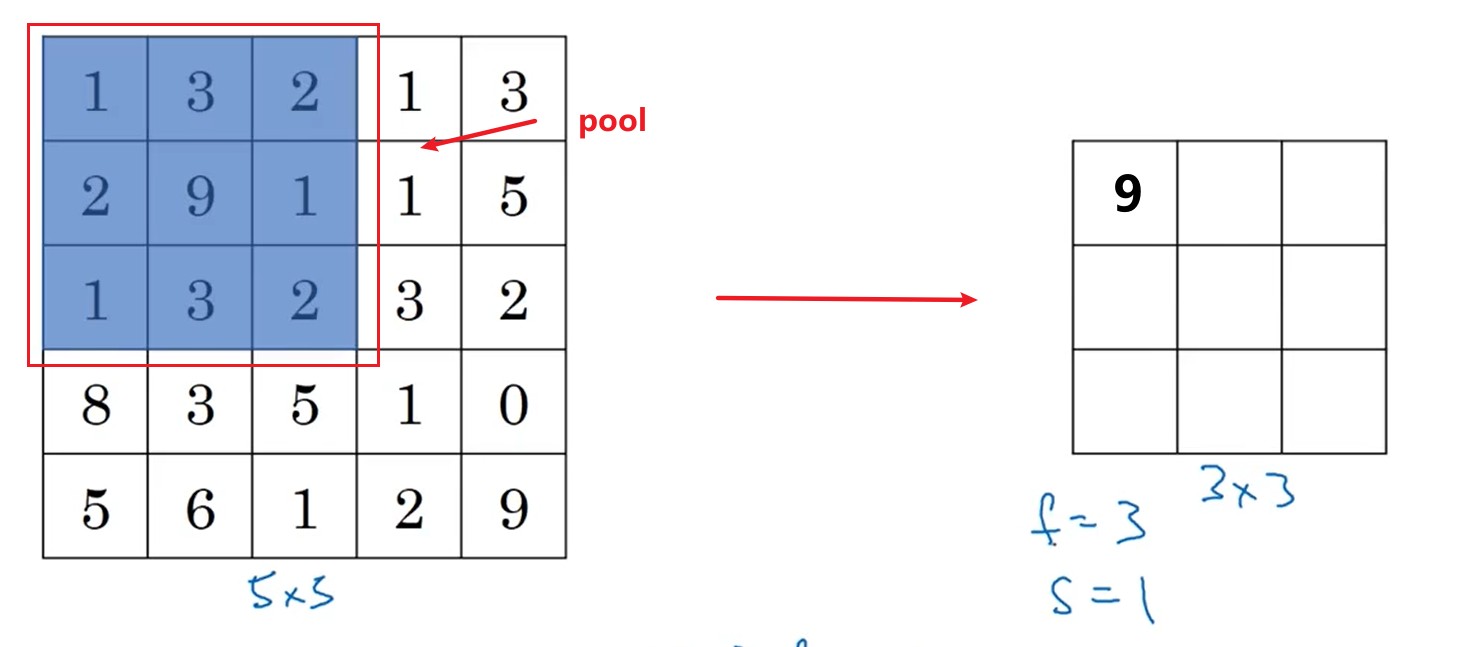
不同于卷积，池化的作用是将原来的像素，按照块操作，进行压缩处理。 根据压缩数据方式的不同分为：

• max pooling，区域内的最大值；
• average pooling，区域求平均值。

no=⌊ni−fs+1⌋(6.1)no​=⌊sni​−f​+1⌋(6.1)

​

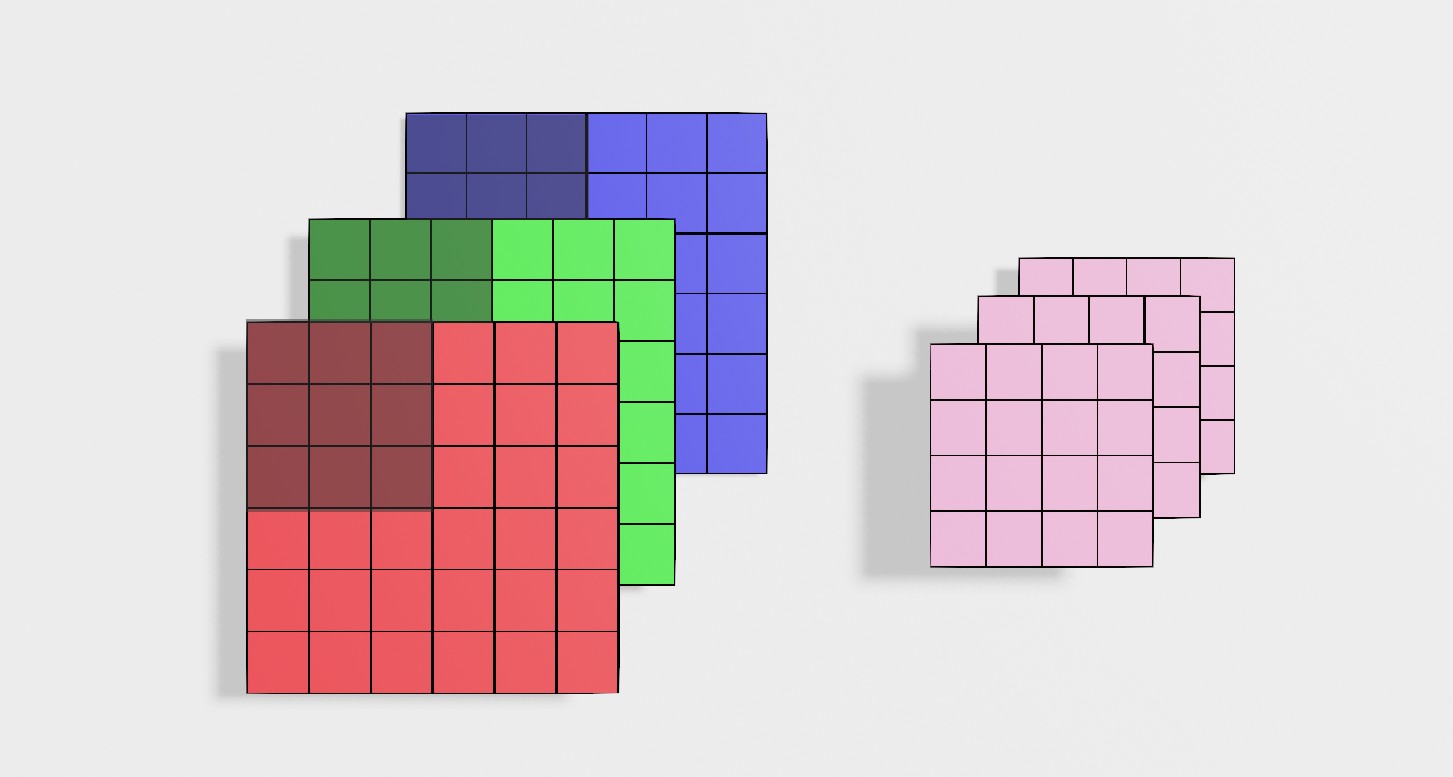
Note

• 对于pooling的计算，每一个通道分别进行一次计算，输出结果通道数不改变。
• pooling涉及的超参数，训练集训练时视为常量。

3.3 卷积神经网络模型

​

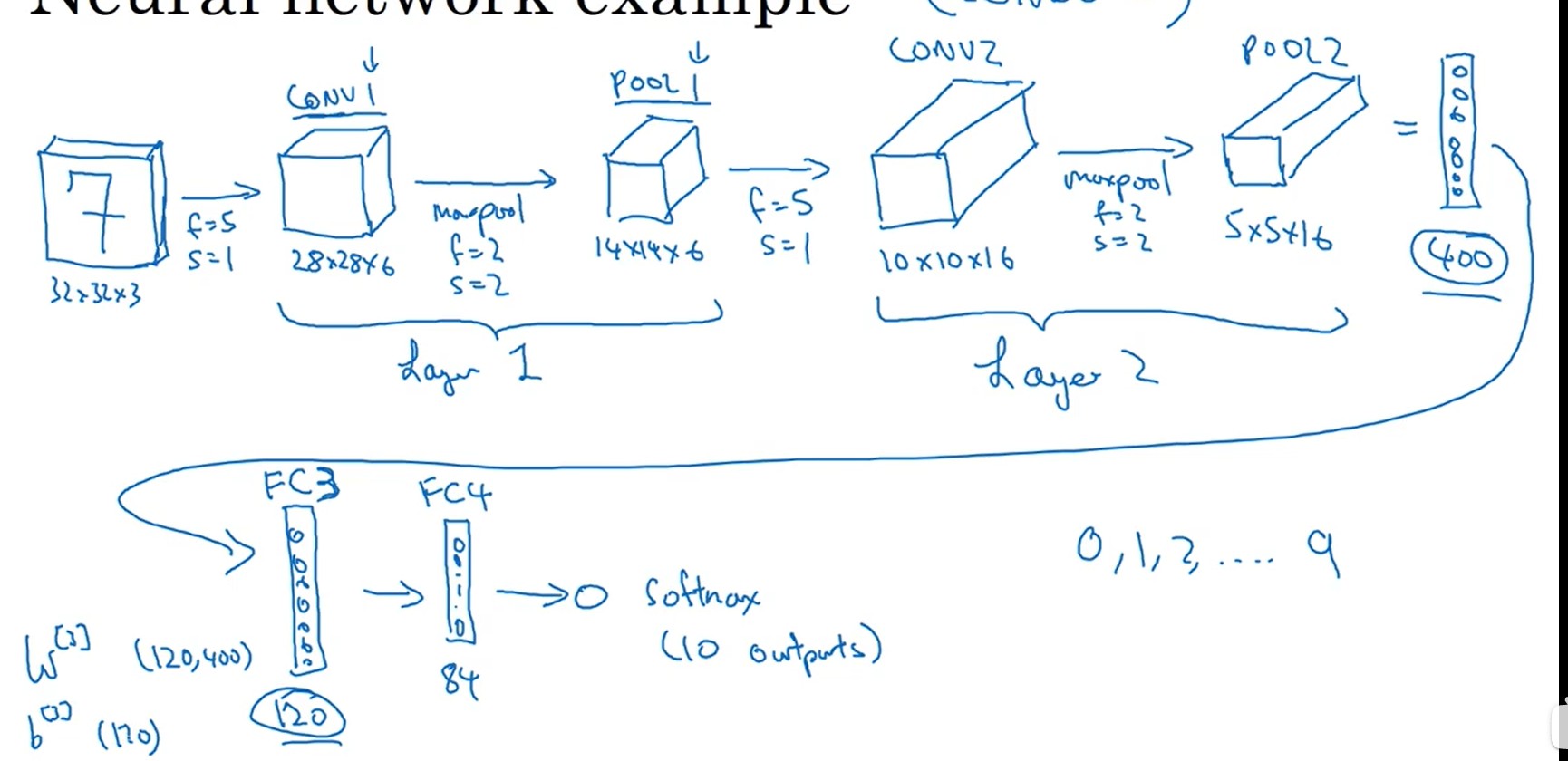
• 图像刚输入的时候，靠卷积和池化提取特征，降低图片参数数量。
• 输出就是靠全连接网络（BP网络）和分类器获取估计结果。

3.4 卷积的作用

​

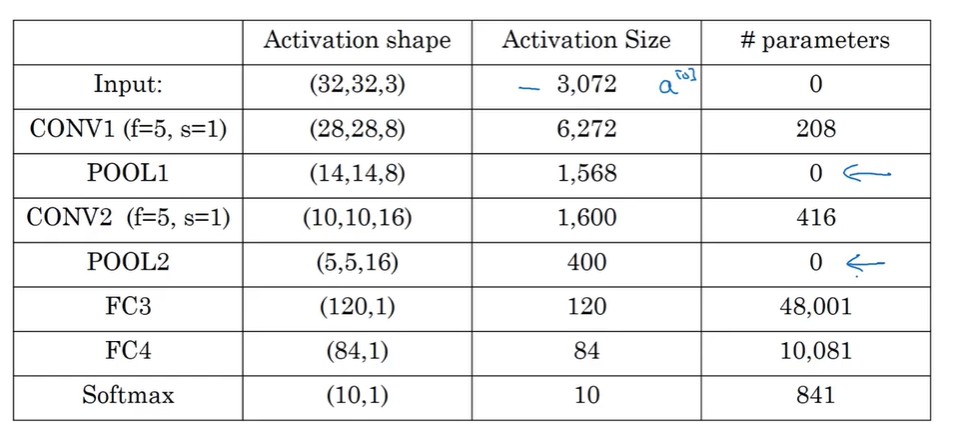
与普通神经网络相比，卷积网络大大降低了超参数的量，实现了对图像像素的压缩和特征提取。

• parameter sharing：用于一次过滤的过滤器都是一样的，数据处理过程统一，也降低了超参数的量。
• sparsity of connection：每个像素只能影响局部的结果，符合常规认知。

四、1x1 卷积

​

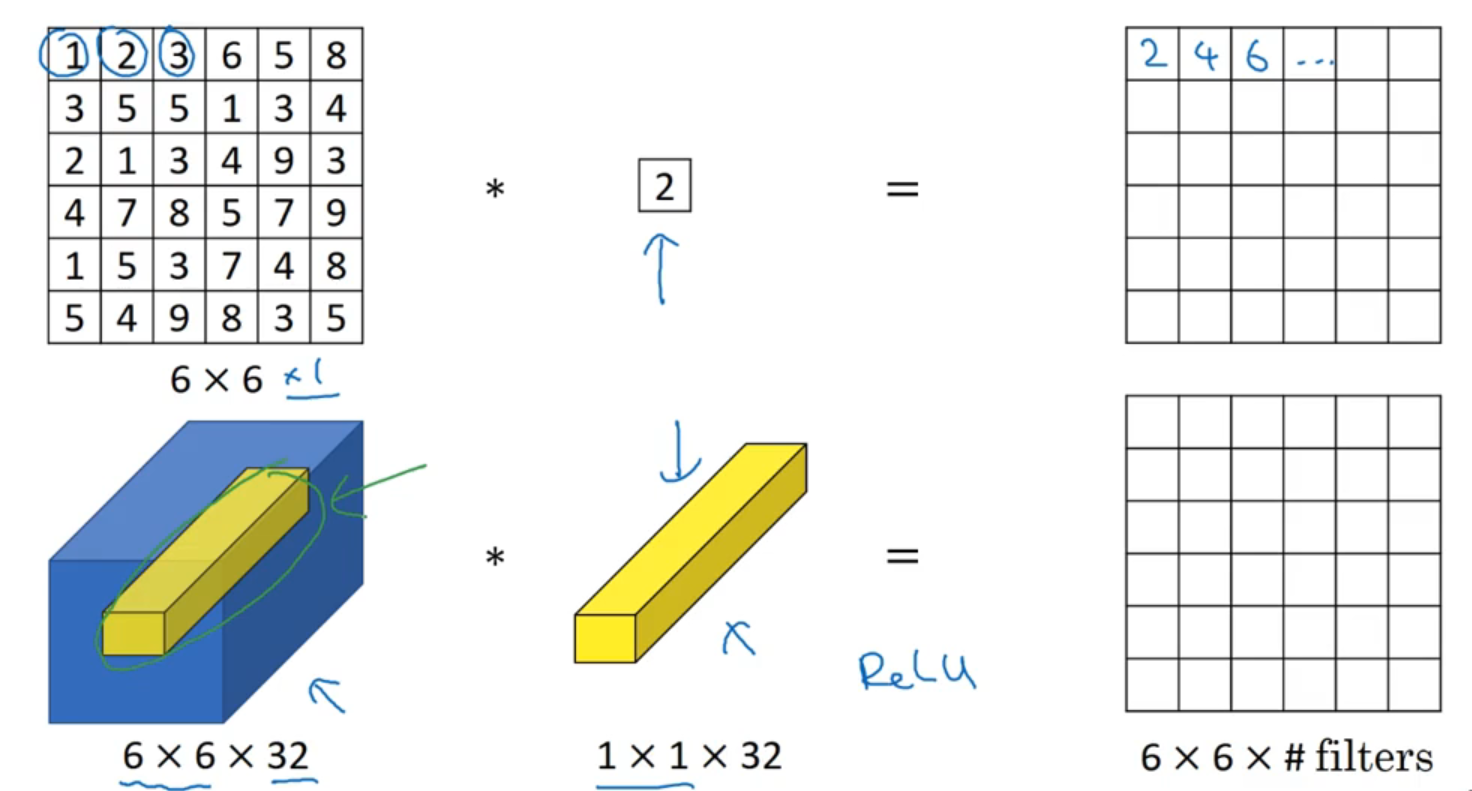
• 压缩信道并改变信道维度： 对于单信道的输入数据来说，1x1的卷积没啥鸟用，结果就是在原理的输入上通乘一个数，并没有对特征进行提取。但是对于多信道的输入数据，1x1 卷积实现了对输入特征图在信道方向上的压缩，例如 6x6x32 的输入，经过1 个 1x1 卷积核的卷积结果为 6x6x1，经过2个 1x1卷积核的卷积结果为 6x6x2

• 缩减计算次数与参数：

  没有引入1x1 卷积步骤，其乘法计算次数为：(28x28x32)x(5x5x192)=120,422,400；卷积核系数个数为：5x5x192x32=153600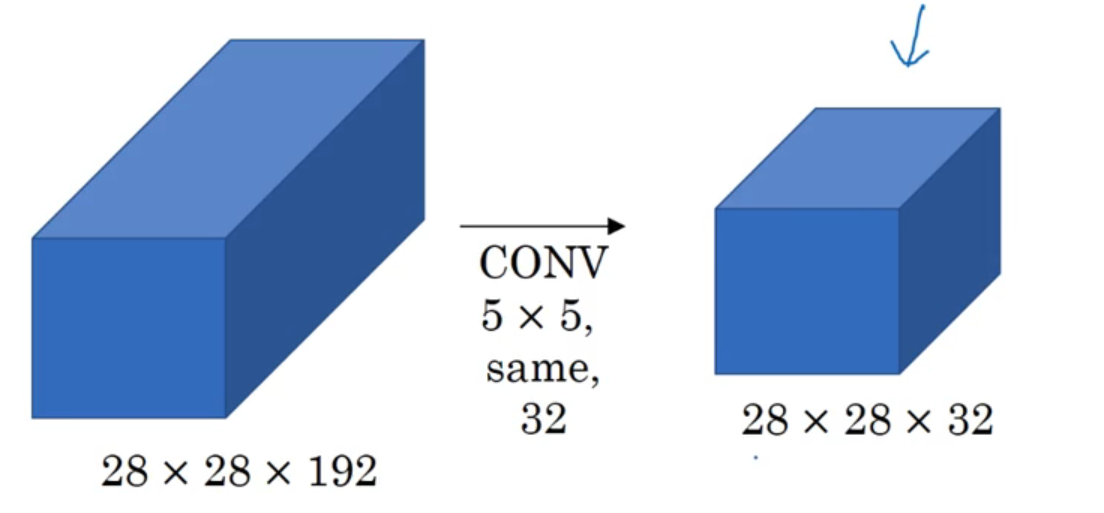

  ​

  引入1x1卷积步骤后，其乘法计算次数为：(28x28x16)x192 + (28x28x32)x(5x5x16) = 12,433,648；卷积核系数个数为：192*16+5x5x16x32=15872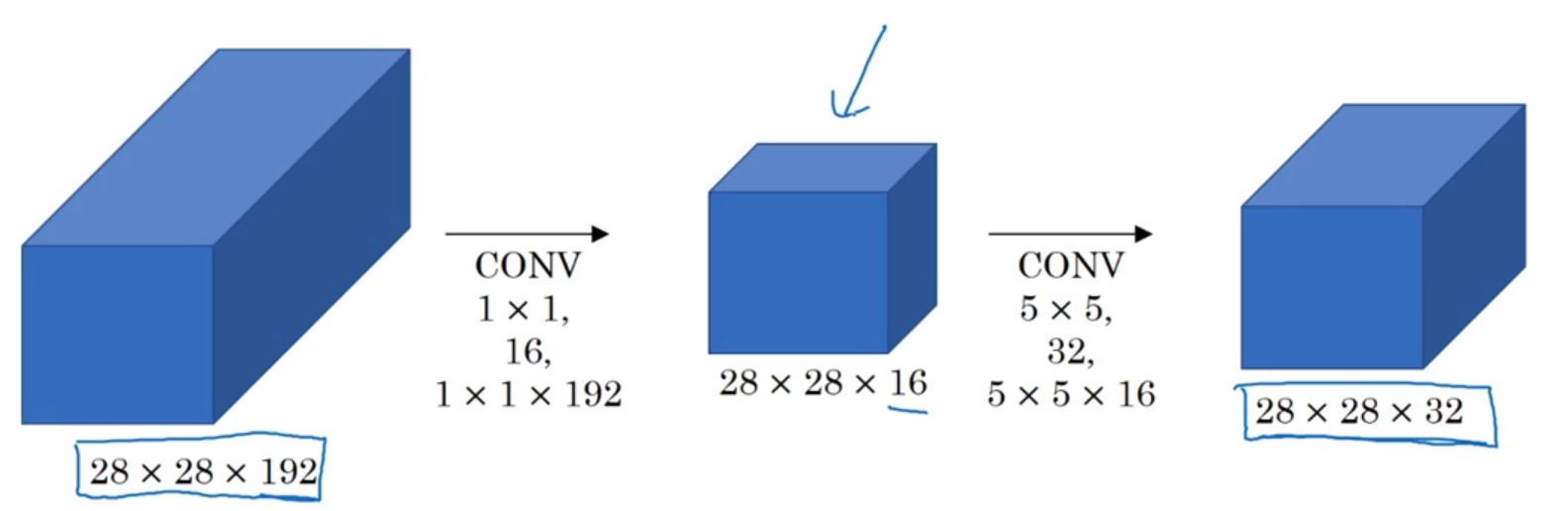

  ​

  在中间步骤中，引入1x1卷积，乘法计算量缩小为原来的 10.3 %，参数个数缩减为原来的10.3 %

五、卷积网络模型

5.1 经典卷积网络

5.1.1 LeNet-5

​

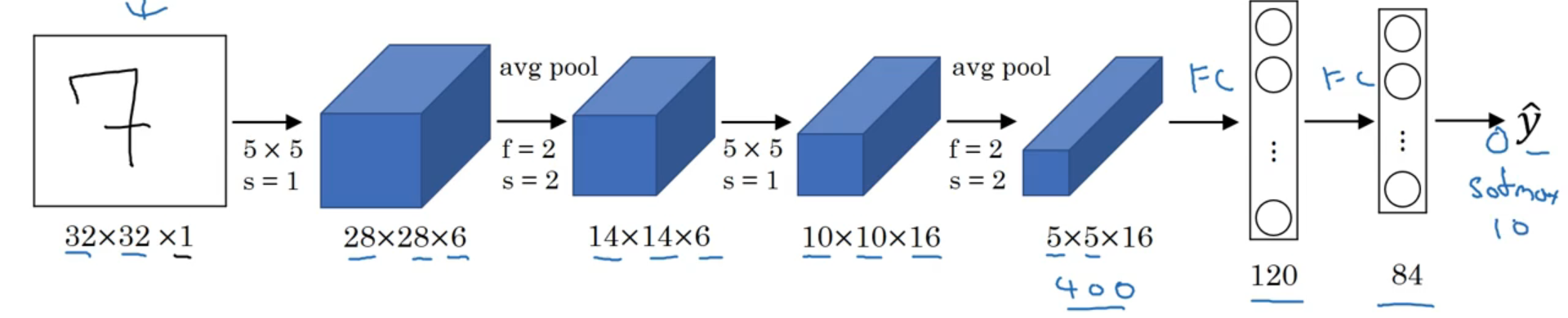
• 作用： 识别手写数字
• 特点： 提出了每个「卷积层」之后添加一个「池化层」

5.1.2 AlexNet

​

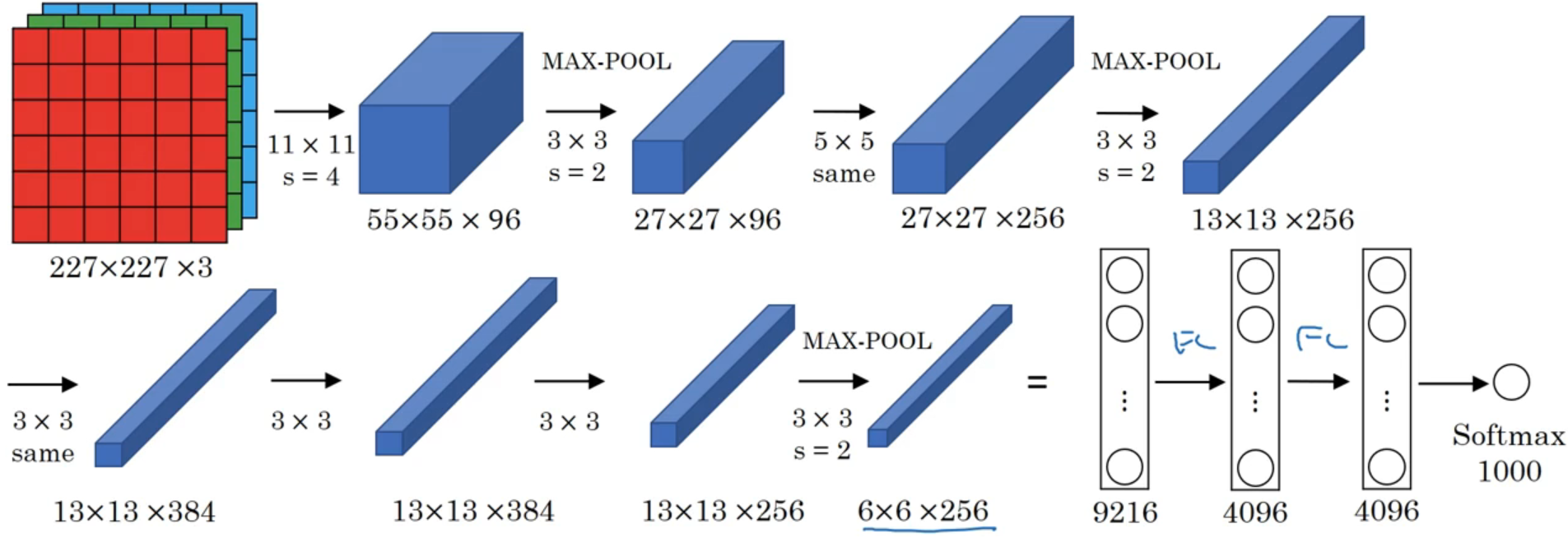
• 作用： 给包含有1000种类别的共120万张高分辨率图片进行分类
• 特点： 在隐含层中设置了大量的参数，并且卷积层的通道数也比较大
• 意义： 从这个网络模型开始，计算机视觉的研究开始重视深度学习的应用。

5.1.3 VGG16

​

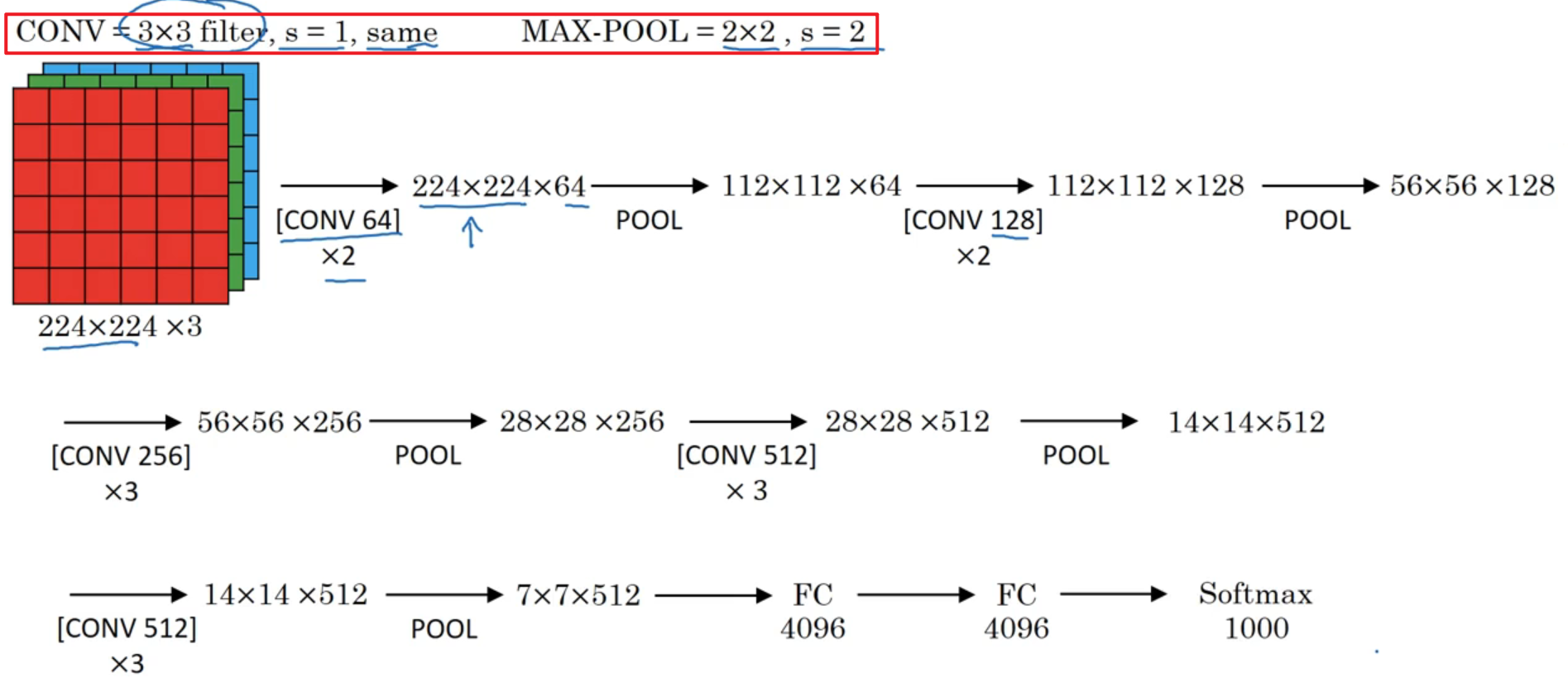
• 作用： 图像分类
• 特点：
  1. 利用最简单的卷积和池化进行网络搭建，卷积核的尺寸越小，对于图片特征就更加的敏感。
  2. 更加丧心病狂的添加隐含层信道

5.2 残差网络

​

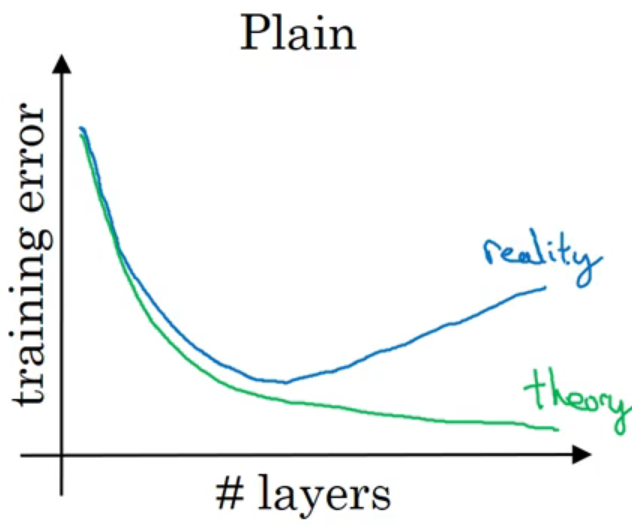
• 作用： 随着传统深度学习网络 Plain network 加深时，其模型预测结果并非越来越好，反而会变得更差。为了实现深层网络的学习，何凯明等人提出了「残差网络」，在 dlib 库中，人脸特征描述符的预测，就利用了该网络。

​

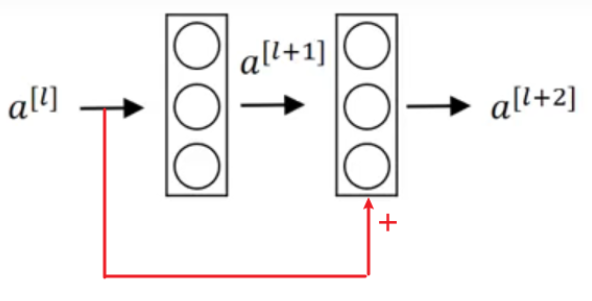
• 残差块： 在计算 a[l+2]a[l+2] 时，添加了 a[l]a[l] 的结果

  a[l+2]=g(W[l+2]a[l+1]+b[l+2]+Ma[l])a[l+2]=g(W[l+2]a[l+1]+b[l+2]+Ma[l])

  其中 MM 为维度转换矩阵，当 a[l]a[l] 与 al+2al+2 的维度不一样时，需要对 a[l]a[l] 的维度进行转化，需要当作网络参数进行学习；当 a[l]a[l] 与 al+2al+2 的维度一样时 MM 就是一个单位阵，不要学习。

• 残差块工作原理： 假设网络模型的训练结果为 W[l+2]=0,b[l+2]=0W[l+2]=0,b[l+2]=0，则

  a[l+2]=g(0+Ma[l])a[l+2]=g(0+Ma[l])

  从结论上来看看，a[l+2]a[l+2] 的计算结果只与 a[l]a[l] 相关， 即 [l+1][l+1] 层网络被屏蔽了，网络隐含层被减少。又由于 W[l+2]=0,b[l+2]=0W[l+2]=0,b[l+2]=0 只是极端情况，实际中出现概率低， [l+1][l+1] 层肯定会起点作用的，因此最终的隐含层多的网络模型肯定比隐含层少的效果要好。

• 卷积网络： 在卷积网络中的使用方法同理。

  ​

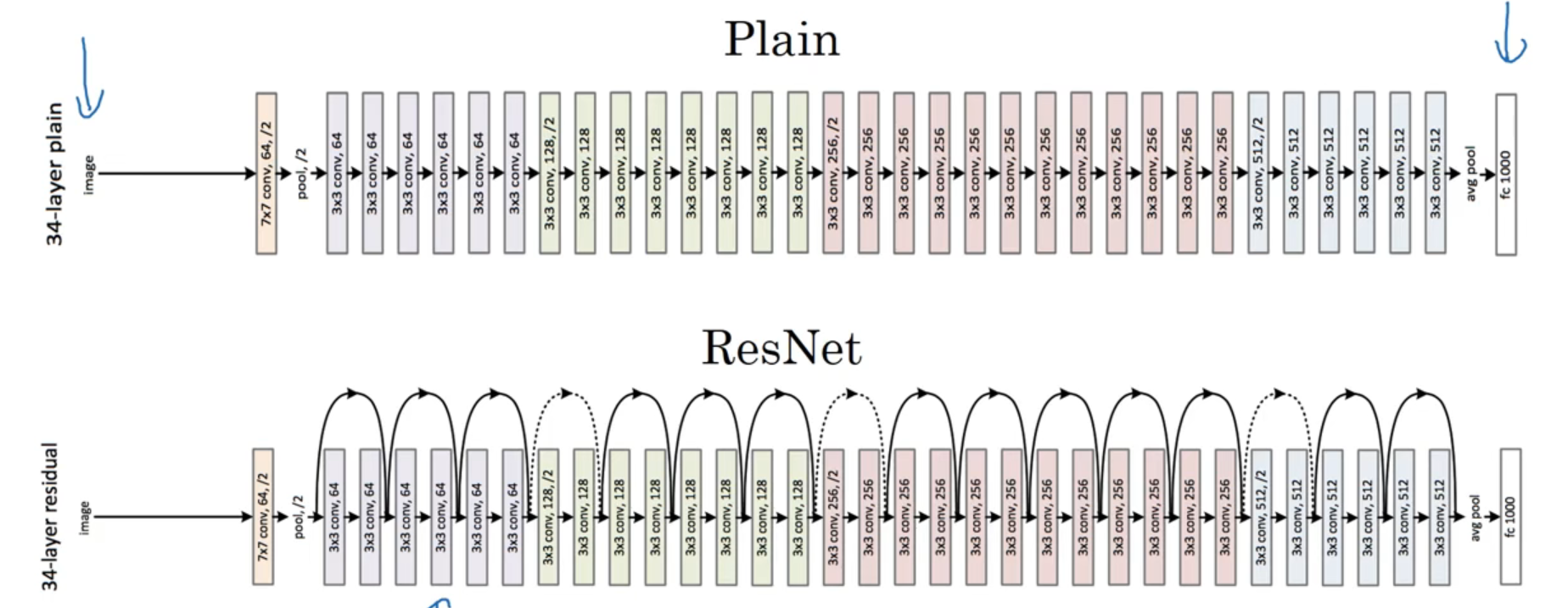
5.3 inception 网络

• 作用： 当我们不知道当前卷积层采用哪个类型卷积核更好，还是说当前层不卷积而是进行池化的时候，这是就可以利用 inception 网络，让模型自己判断。

​

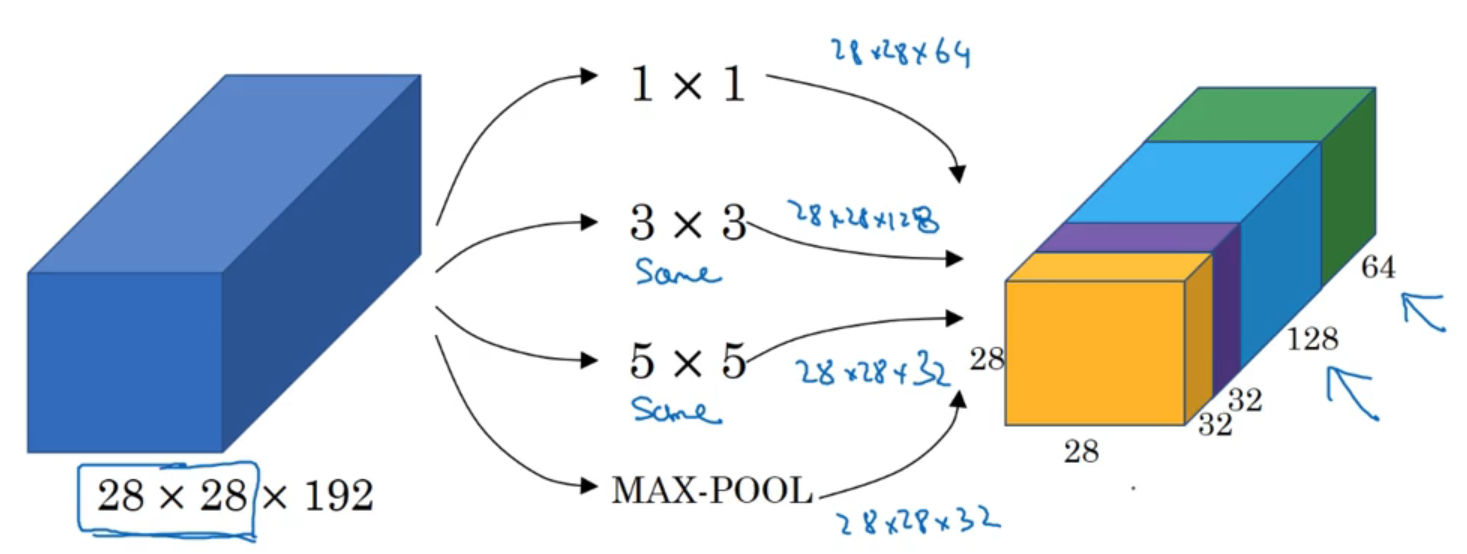
• inception层： 将不同卷积核以及池化后的结果在信道方向上堆叠起来，组合成当前隐含层，这个组合层就是「inception层」。从上图中可以看出，这样设计模型后，参数量核计算量都挺大，因此应用 1x1 卷积核，实现计算量与参数压缩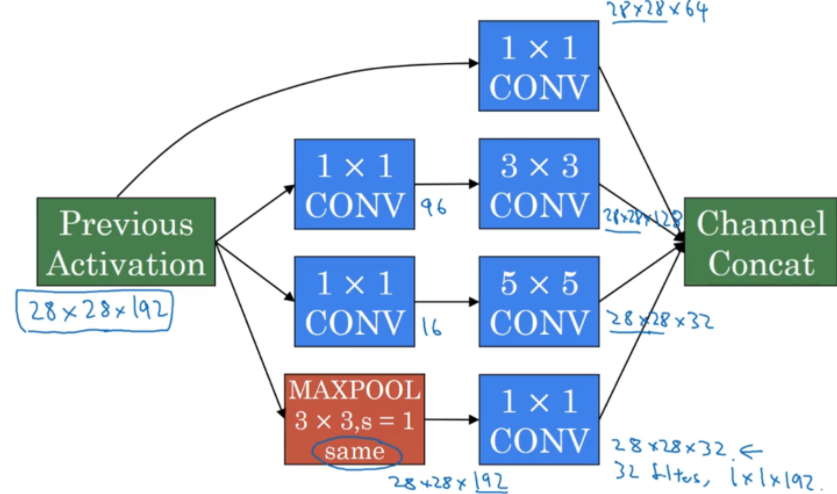

  ​

  其中为了保持池化后特征图的「尺寸」不变，这里在池化之前，首先对原图进行了 padding

• inception 网络： 使劲堆叠 inception 层

  ​

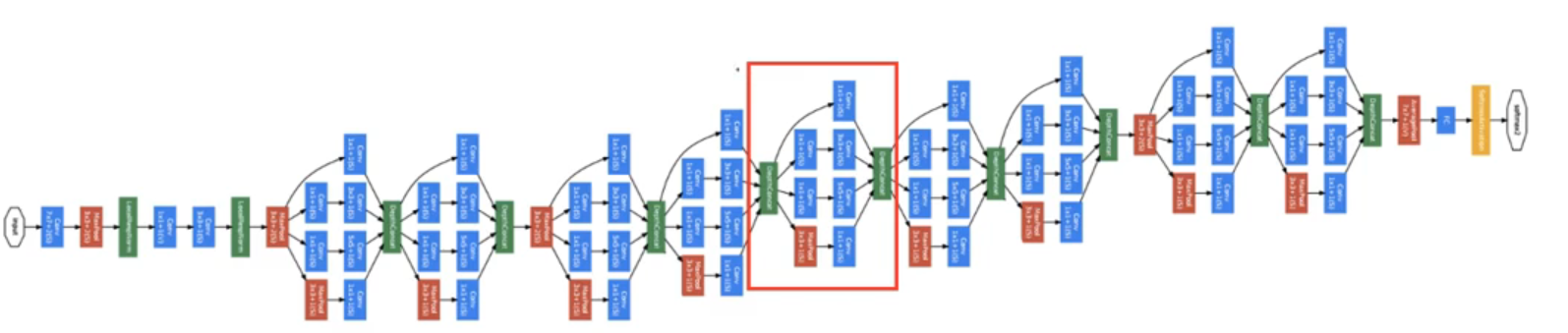
5.4 GoogleNet

​

在 inception 网络的基础上， 为了避免梯度消失，增加了两个「辅助分类（上图红框）」用于向前传导梯度。

5.5 迁移学习

Tip

从头训练自己的模型，费时又费力，可以通过迁移学习抄别人的网络，实现偷懒。

• 方法一： 将红色框框住的部分「系数冻结」，重新训练自己任务的「输出层」

  ​

• 方法二： 对别人模型的「前面几层」进行系数冻结，后面部分自己重新训练或者设计

  ​

• 方法三： 用给人的「前面几层」是作为一个「特征转换函数」，用该特征函数对自己的样本进行预处理，之后再根据预处理结果进行模型设计

  ​

• 方法四： 将别人的的模型权重系数初始化自己模型，之后重新训练

为什么要选择别人模型的「前面几层」？

越靠前卷积层，着重的是对「局部特征」的提取；越靠后的层级则是注重对检测目标的「整体特征」进行过滤，例如对于第一层卷积得到的特征图的一个像素位置对应「原图」的3x3，第二层卷积得到的特征图的一个像素位置对应「原图」的 5x5，即越靠后的卷积层，看见原图区域越广，「感受野」越大。

• 感受野：特征图上的一个像素位置对应原始图多大区域。

​

5.6 全连接层卷积化

​

在传统网络中，经过卷积层特征提取后的数据最后都会接入全连接层进行最终结果的输出，然而接入全连接层后，就会导致输入的图片尺寸必须固定。

​

由于多通道的1x1卷积运算和全连接层的远算其实是类似，就可以通过 1x1 的卷积操作将原来的全连接层转化为卷积层。

六、目标检测

6.1 概念区分

计算机视觉需要解决的问题有：分类、检测、分割。

• classification： 单目标分类，区分图片里的类容是人、动物、植物或者汽车等，例如 softmax 层、二分类问题。

• classification localization： 目标定位，单目标分类并标记出目标位置，即画出目标的 bounding box

  ​

• object detection： 目标检测，从图片中查找出所有的目标物体，并绘制所有目标的 bounding box

  ​

• semantic segmentation： 语义分割，将目标物体从背景图片分离出来，但是目标物体之间不做区分

  ​

• instance segmentation： 实列分割，将目标物体从背景图片分离出来，并且还要区分各个目标物体

  ​

6.2 目标定位

​

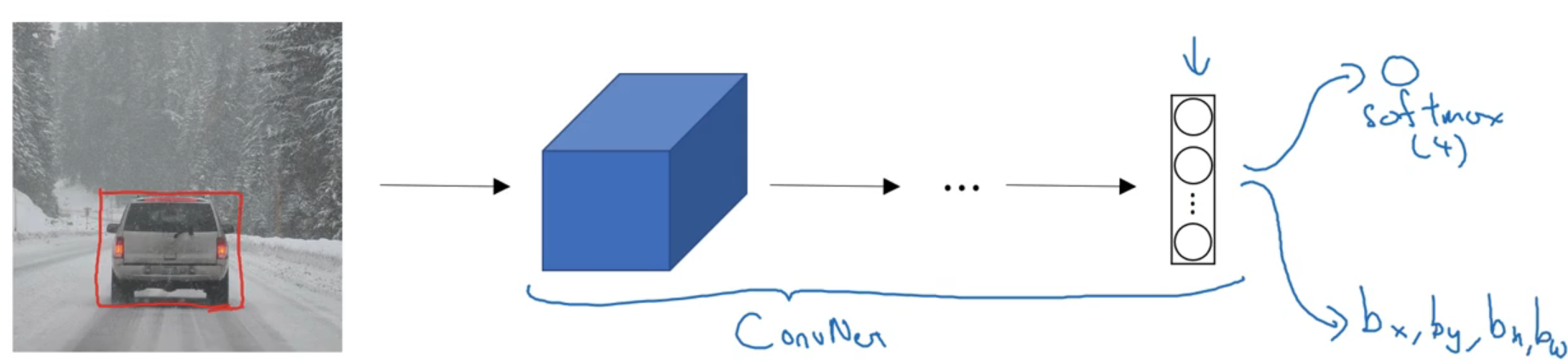
在之前网络中，输入图片，然后图片经过卷积、池化、全连接后，最后接入 softmax 层就实现了图像分类。为了实现目标定位，只需在原来分类的基础上，添加矩形框

y^=[pc,bx,by,bh,bw,c1,c2,c3,⋯ ]Ty^​=[pc​,bx​,by​,bh​,bw​,c1​,c2​,c3​,⋯]T

其中 pcpc​，图片中是否存在目标物体；bx,bybx​,by​，矩形框的中心点；bh,bwbh​,bw​，矩形框的长、宽；c1,c2,c3,⋯c1​,c2​,c3​,⋯，检测目标的分类

6.3 特征点检测

​

landmark detection：特征点检测，标记出要检测目标中的关键点，例如人脸关键点、手势识别、骨骼关键点。网络输出添加特征点坐标 (xi,yi)(xi​,yi​)，并且关键点的输出顺序固定。

6.4 目标检测

6.4.1 滑动窗口

​

步骤：

1. 利用滑动窗口在输入图像中扫描，对原图进行裁剪
2. 利用训练好的「图片分类器」对裁剪的图片进行类型判别，判别结果若是检测目标，滑动窗口的当前位置就是目标位置。

在dlib库中的人脸检测就采用了该思路，首先对目标图片提取 HOG 特征，然后利用 SVM 支持向量机对特征进行判别。

6.4.2 卷积滑动

• 原因： 利用传统的滑动窗口对目标进行检测，一个区域一个区域的遍历，然后对每个区域又进行一次检测，这个是是否消耗计算机性能，为了加快计算速度可以将「滑动窗口」改为「卷积」。

• 原理： 首先将原来的图片分类模型的全连接层卷积化

  ​

  这里假设分类模型的输入图片大小为3x3，首先进行3x3卷积，然后模仿全连接层进行两次 1x1 卷积，其中对于模型中的信道数都忽略了。

  按照原来的分类模型思路，就是每次检测只输入一张 3x3 的图片，然后经过模型处理后，得到该图片的分类结果。但是，对全连接层进行卷积化后，对于图片的输入大小将不再限制。因此，可以直接将整张图片输入分类模型中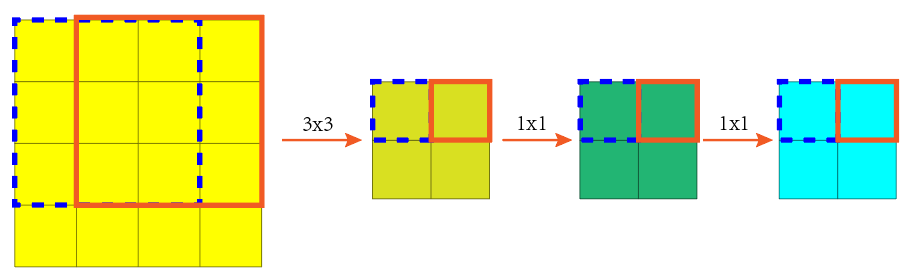

  ​

  假设原始图片的大小为 4x4 对该图片直接进行分类模型运算，输出结果就为 2x2，对于该输出结果的每个格子就对应了原图中的 4 个3x3的滑动窗口，即卷积的结果就是滑动窗口的计算结果。

• 优点： 将滑动窗口卷积化，会大大加快滑动窗口计算速度。 上述案例，对模型进行简化，看来计算速度是一样的，其对于复杂模型而言，卷积代替滑动，就省略了大量的重复操作。

  ​

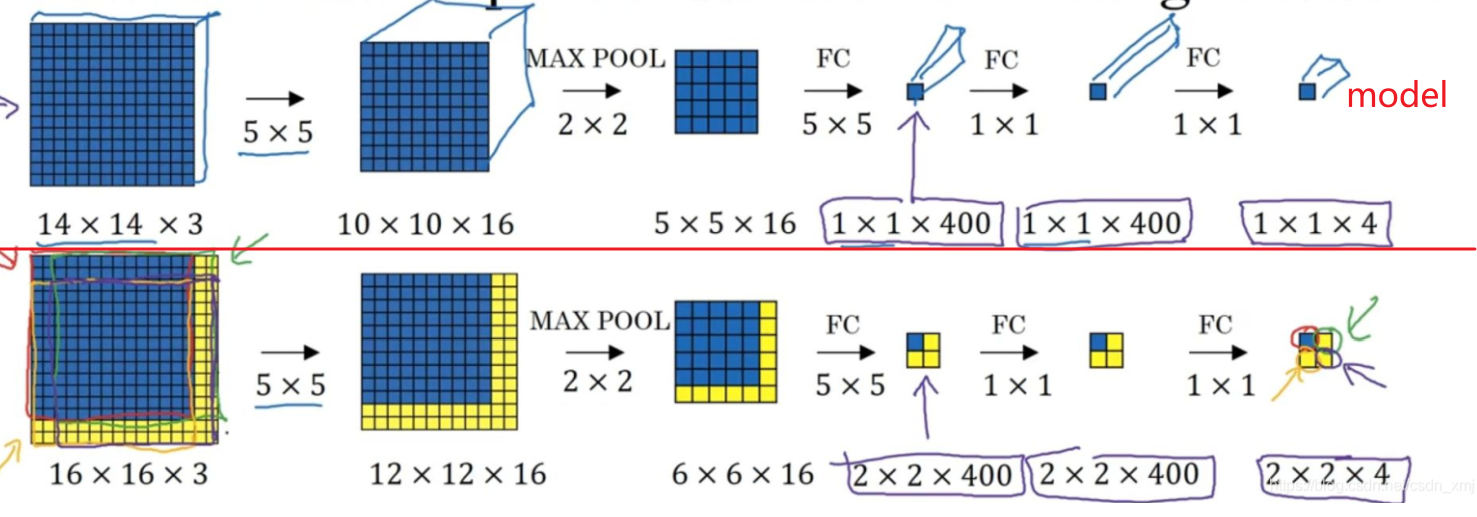
  以上图模型的第一层卷积层为例，滑动窗口大小为 14x14，步长为 2，滑动4次。

  • 传统滑动窗口进行检测，第一层卷积乘法运算次数：4x(10x10x16)x(5x5x3) = 480,000
  • 卷积检测，第一层运乘法运算次数：(12*12*16)*(5*5*3)=172,800

  6.4.3 R-CNN 算法

传统的滑动窗口只是利用滑动窗口漫无目的的一块区域一块区域的扫描图片，然而通常一张图片中，背景区域是要多余目标的区域，滑动窗口法就检测了许多无意义的背景区域，加大了运算量。R-CNN 算法的思想就是，提前从图片中筛选一些有意义的候选区域，然后再对这些区域进行目标分类。

可以通过图像分割，提前筛选区域。如下图，利用图片分割将输入图片拆分成了不同区域，然后利用 OpenCV 中的「轮廓检测」，就能将每个区域的 bounding box 提取出来，并对这些外接矩形进行筛选，最后剩下的 bounding box 就是我们进行检测的候选框。

​

6.4.3 YOLO 算法

支持向量机

1. 概念介绍

• 支持向量机（support vector machines, SVM）：一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性「分类器」，间隔最大使它有别于感知机；SVM还包括「核」技巧，这使它成为实质上的非线性分类器。

• 分类基本思想： 根据高中数学知识，可以知道在二维平面上画一直线 f(x,y)=0f(x,y)=0 ，就能将平面划分为两个部分：直线上方 f(x,y)>0f(x,y)>0 ；直线下方 f(x,y)<0f(x,y)<0。根据这个特性就能通过一条直线将平面的内的数据点 (x,y)(x,y) 划分为两个区域，即实现了分类。

  ​

• 支持向量机思想： SVM 的目标是对未知的输入数据也实现分类，这就使得「超平面」的鲁棒性要好。因此，SVM 在「决策超平面」的基础上，引入了「正超平面」与「负超平面」，正负超平面与决策超平面之间就形成了两个缓冲区域。决策超平面两侧的缓冲区域越宽，就说明数据的差异越大，那么利用决策超平面对数据进行分类时，准确度也越高。

  ​

• 超平面： 二维数据通过直线能分为两部分；三维数据能通过平面划分为两部分。对数据进行划分的界限就称之为「超平面」。

  WTX+b=0,W=[w1,⋯ ,wn]T,X=[x1,⋯ ,xn]TWTX+b=0,W=[w1,⋯,wn]T,X=[x1,⋯,xn]T

  • 正/负超平面：将决策超平面在垂直方向上，向上或向下移动距离 cc。

    WTX+b=+cWTX+b=−cWTX+b=+cWTX+b=−c

    由于 cc 是上下移动距离，c=0c=0 就没啥卵用了，因此得
    WTX+bc=+1WTX+bc=−1cWTX+b=+1cWTX+b=−1

    系数除以系数，还是系数，因此可以将 cc 与其他系数合并
    WTX+b=+1WTX+b=−1WTX+b=+1WTX+b=−1

Tip

现在关于 SVM 的模型已经知道了，实现 SVM 就需要通过样本数据求解出系数 W,bW,b。然而，超平面的取法可以有多种情况，我们的求解目的肯定是想找到最优的，因此，求解 W,bW,b 肯定是一个寻优问题。

2. 硬间隔模型

2.1 模型介绍

• 思想： 为了更好的区分两边的数据，就需要决策超平面与正负超平面之间的距离（间隔）最大。最好的情况就是，正负超平面就在两边样本值的边界上，决策超平面就在正负超平面的中间，这样就能实现间隔 dd 最大。

  ​

• 支持向量： 处于正/负超平面上的样本点。

• 优化目标： 找出 W,bW,b 使得间隔距离 dd 最大。从图中也可以看出，距离 dd 取决于样本中的「支持向量」

2.2 目标函数

寻优目标是使得 dd 最大化，因此首先得求解出 dd。
​

假设在正/负超平面上取得两个支持向量分别为 XmXm​ 、 XnXn​，则正负超平面满足

WTXm+b=−1WTXn+b=+1WTXm​+b=−1WTXn​+b=+1​

两式子相减

WT(Xn−Xm)=2WT(Xn​−Xm​)=2

根据向量乘法有

WT(Xn−Xm)=∣∣W∣∣ ∣∣Xn−Xm∣∣cos⁡θWT(Xn​−Xm​)=∣∣W∣∣ ∣∣Xn​−Xm​∣∣cosθ

从图上可知

d=∣∣Xn−Xm∣∣cos⁡θd=∣∣Xn​−Xm​∣∣cosθ

最后得到

d=2∣∣W∣∣d=∣∣W∣∣2​

要使得 dd 最大，也就是使得 ∣∣W∣∣∣∣W∣∣ 最小，优化目标函数就可以定义为

min: f(W,b)=∣∣W∣∣22min: f(W,b)=2∣∣W∣∣2​

目标函数的最优解，就是我们需要的 SVM 模型系数 W,bW,b

2.3 约束条件

确保所找到的超平面的有效性，就需要将两类数据分别限制在正负超平面的两边。
​

对两边的样本建立标签值

• y=−1y=−1 时，为负超平面一方的样本，即满足 WTX+b≤−1WTX+b≤−1
• y=+1y=+1 时，为正超平面一方的样本，即满足 WTX+b≥+1WTX+b≥+1

整合上面两种情况，最后约束方程就为

y(WTX+b)≥1y(WTX+b)≥1

2.4 优化模型

拉格朗日乘数法大礼包

• 拉格朗日乘数：00:00
• 对偶函数、对偶问题：13:26
• 凸集、凸函数、仿射集：19:00
• 弱对偶、强对偶：25:55
• slater条件、KKT条件：36:42

2.4.1 模型转化

问题模型：

min: f(W,b)=∣∣W∣∣22st: gi(W,b)=1−yi(WTXi+b)≤0min:st:​ f(W,b)=2∣∣W∣∣2​ gi​(W,b)=1−yi​(WTXi​+b)≤0​

其中变量为 W,bW,b

从问题模型，可以看出这是一个「凸优化问题」。利用「拉个朗日乘数法」对该问题进行求解，将上式约束问题改写为拉格朗日形式

L(W,b,λ)=f(W,b)+∑iλigi(W,b)L(W,b,λ)=f(W,b)+i∑​λi​gi​(W,b)

其中

{λi=0gi(W,b)<0λi>0gi(W,b)=0{λi​=0gi​(W,b)<0λi​>0gi​(W,b)=0​

上述拉格朗日乘数的「对偶函数」

h(λ)=min⁡W,bL(W,b,λ)λi≥0h(λ)=W,bmin​L(W,b,λ)λi​≥0

进一步 「对偶问题」 就为

max⁡: h(λ)st: λi≥0max:st:​ h(λ) λi​≥0​

又由于原问题是「凸优化问题」，同时原问题的约束是仿射线性约束，进一步满足「slater条件」，因此，h(λ)h(λ) 与 f(W,b)f(W,b) 是「强对偶」

h(λ∗)=f(W∗,b∗)h(λ∗)=f(W∗,b∗)

通过强对偶关系，就实现了原优化问题到对偶问题的转换。

2.4.2 对偶问题

求解对偶函数

h(λ)=min⁡W,bL(W,b,λ)λi≥0h(λ)=W,bmin​L(W,b,λ)λi​≥0

求解偏导

dLdW=W−∑iλiyiXidLdb=−∑iλiyidWdL​dbdL​​=W−i∑​λi​yi​Xi​=−i∑​λi​yi​​

使得 L(W,b,λ)L(W,b,λ) 最小的 W，bW，b 满足

W−∑iλiyiXi=0∑iλiyi=0W−i∑​λi​yi​Xi​i∑​λi​yi​​=0=0​

将上述式子回代得

L(W,b,λ)=∣∣∑iλiyiXi∣∣22+∑iλi[1−yi(∑jλjyjXj)TXi−yib]=12∑i∑jλiλjyiyjXiTXj+∑iλi−∑i∑jλiλjyiyjXiTXj−b∑iλiyi=∑iλi−12∑i∑jλiλjyiyjXiTXjL(W,b,λ)​=2∣∣∑i​λi​yi​Xi​∣∣2​+i∑​λi​[1−yi​(j∑​λj​yj​Xj​)TXi​−yi​b]=21​i∑​j∑​λi​λj​yi​yj​XiT​Xj​+i∑​λi​−i∑​j∑​λi​λj​yi​yj​XiT​Xj​−bi∑​λi​yi​=i∑​λi​−21​i∑​j∑​λi​λj​yi​yj​XiT​Xj​​

对偶问题就为

max⁡: h(λ)=∑iλi−12∑i∑jλiλjyiyjXiTXjst: λi≥0∑iλiyi=0max: st:​h(λ)=i∑​λi​−21​i∑​j∑​λi​λj​yi​yj​XiT​Xj​ λi​≥0i∑​λi​yi​=0​

其中

{λi=0gi(W,b)<0λi>0gi(W,b)=0{λi​=0gi​(W,b)<0λi​>0gi​(W,b)=0​

求解「对偶问题」，就只用考虑「支持向量」。

2.5 模型求解

利用「 序列最小优化算法」求解「对偶问题」得到最优解 λ∗λ∗，然后回代求得

W∗=∑iλi∗yiXiW∗=i∑​λi∗​yi​Xi​

再利用 W∗W∗ 与 「支持向量」反解 b∗b∗

gi(W∗,b∗)=0gi​(W∗,b∗)=0

3. 核技巧

3.1 概念

​
​

• 思想： 在二维平面，非线性的分类问题无法再通过二维的超平面进行分割，但是，将二维数据升维变为三维数据，这样就能通过三维空间中的超平面，实现对数据的分类。

• 维度变换： 对原来的样本数据 XiXi​ 通过维度变换等到高纬度的数据 T(Xi)T(Xi​) 。其中变换函数为 T()T() 。

  变换后的对偶问题
  max⁡: h(λ)=∑iλi−12∑i∑jλiλjyiyjT(Xi)TT(Xj)st: λi≥0∑iλiyi=0max: st:h(λ)=i∑λi−21i∑j∑λiλjyiyjT(Xi)TT(Xj) λi≥0i∑λiyi=0

• 核函数： 上述变换函数 T(Xi)TT(Xj)T(Xi​)TT(Xj​) 的计算，首先要分别计算 T(Xi)、T(Xj)T(Xi​)、T(Xj​)，然后再计算 T(Xi)TT(Xj)T(Xi​)TT(Xj​) 得到结果。这一套流程下来即浪费空间，又会产生大量计算，那为何不使用一个函数直接得到上面的结果

  K(Xi,Xj)=T(Xi)TT(Xj)K(Xi,Xj)=T(Xi)TT(Xj)

  其中 K()K() 就被称之为「核函数」。 引入核函数后，对偶问题又变为了
  max⁡: h(λ)=∑iλi−12∑i∑jλiλjyiyjK(Xi,Xj)st: λi≥0∑iλiyi=0max: st:h(λ)=i∑λi−21i∑j∑λiλjyiyjK(Xi,Xj) λi≥0i∑λiyi=0

3.2 多项式核函数

K(Xi,Xj)=(c+XiTXj)dK(Xi​,Xj​)=(c+XiT​Xj​)d

对于 c,dc,d 系数选取不同的值，可以产生不同的维度结果。

当 c=1,d=2c=1,d=2 时，就实现了将一个二维数据转换成了一个六维的数据

X=[x1,x2]TY=[1,2x1,2x2,x12,x22,2x1x2]T满足:(1+XiTXj)2=YiTYj满足:​X=[x1​,x2​]TY=[1,2​x1​,2​x2​,x12​,x22​,2​x1​x2​]T(1+XiT​Xj​)2=YiT​Yj​​

其中，cc 值不要选择 00 。
​

3.3 高斯核函数

Warning

高斯。。。又来了 (⊙﹏⊙)

K(Xi,Xj)=e−γ∣∣Xi−Xj∣∣2K(Xi​,Xj​)=e−γ∣∣Xi​−Xj​∣∣2

• 含义： 高斯核函数描述了样本 Xi、XjXi、Xj 的相似程度，样本越相似 K(Xi,Xj)K(Xi,Xj) 的值越大。
  • γγ：控制样本值 Xi、XjXi、Xj 要多靠近，才能产生较高的相似度。γγ 越大，Xi、XjXi、Xj 要足够靠近，才会评判两个样本有较高相似度。

​

• 特点： 高斯核函数可以将，转换后的维度扩展到无限。

​

4. 软间隔模型

4.1 模型介绍

​

• 硬间隔的缺陷： 在硬间隔中，我们认为所有的样本点都没有误差，但是，当样本点中存在误差时（如图所示产生损失的黄点），就会直接导致正/负超平面间隔的减少（正/负超平面的位置取决于「支持向量」，即边界样本点）。

• 软间隔： 进行 SVM 建模时，需要过滤掉误差样本点的影响，然后再进行超平面寻优，这样得到的正负超平面之间的间隔，称之为软间隔。

4.2 铰链损失函数

​

• 有误差点的损失程度：根据约束条件可知，当样本点不在自己的分类区域时

  yi(WTXi+b)−1<0yi(WTXi+b)−1<0

  因此就利于约束条件的偏离程度来定义损失值
  ε=1−yi(WTXi+b)ε=1−yi(WTXi+b)

• 无误差点的损失程度：

  ε=0ε=0

综上，得到最终的样本点「铰链损失函数」

ε=max⁡(0,1−yi(WTXi+b))ε=max(0,1−yi​(WTXi​+b))

4.3 模型求解

在硬间隔模型中，引入损失函数

min: f(W,b)=∣∣W∣∣22+c∑iεist: gi(W,b)=1−yi(WTXi+b)−εi≤0εi≥0min:st:​ f(W,b)=2∣∣W∣∣2​+ci∑​εi​ gi​(W,b)=1−yi​(WTXi​+b)−εi​≤0εi​≥0​

其中 cc 控制着对误差样本点容忍程度，cc 越大，就认为误差样本点越少。然后写出该该问题拉格朗日乘数形式

L(W,b,ε,λ,u)=∣∣∑iλiyiXi∣∣22+∑iλigi(W,b)−∑iuiεiL(W,b,ε,λ,u)=2∣∣∑i​λi​yi​Xi​∣∣2​+i∑​λi​gi​(W,b)−i∑​ui​εi​

其中，将损失 εε 当作了一个变量。获取原问题的对偶问题

max⁡: h(λ)=∑iλi−12∑i∑jλiλjyiyjK(Xi,Xj)st: λi≥0∑iλiyi=0c=λi+uimax: st:​h(λ)=i∑​λi​−21​i∑​j∑​λi​λj​yi​yj​K(Xi​,Xj​) λi​≥0i∑​λi​yi​=0c=λi​+ui​​

求解方法就和硬间隔问题一样了。

Tip

由于在约束 g(W,b)g(W,b) 中引入了 εε ，这就导致 (W,b)(W,b) 的系数值取决于「支持向量」与「误差样本」。

5. 多分类问题

• 成对分类：两两之间建立一个 SVM。例如，区分A、B、C数据，则 A 与 B 建立一个分类模型；B 与 C 建立一个分类模型；C 与 A 建立一个分类模型。
• 一类对余类：一个类型建立一个 SVM。例如，区分A、B、C数据，则 A 与 「其他」 建立一个分类模型；B 与 「其他」 建立一个分类模型；C 与 「其他」 建立一个分类模型。

符号

​