写在前面
时间序列分析是一种用于分析时间序列数据的方法。时间序列数据是指在时间轴上按照一定的时间间隔 顺序记录的观测值 。这种数据在许多领域都很常见,例如经济学、气象学、金融市场、医学 等。时间序列分析的主要目标是理解数据随时间的变化模式 ,预测未来的趋势,并识别数据中的潜在规律和结构。
时间序列分析的主要步骤:
-
数据预处理 :包括数据清洗、缺失值 处理、去除异常值、对数据进行平滑处理等步骤,以确保数据的质量和一致性。
-
时间序列分解:将时间序列分解为几个组成部分,如趋势(长期增长或下降的方向)、季节性(定期波动,如季节性销售数据)和随机波动(不可预测的短期波动)。
-
建模与预测:选择适当的模型对时间序列进行建模。例如,常用的时间序列模型有自回归模型(AR)、移动平均模型(MA)、自回归滑动平均模型(ARMA)、自回归积分滑动平均模型(ARIMA)等。这些模型可以用于预测未来的数值。
-
模型评估与验证:通过计算残差(预测值与实际值的差异)、检验模型的稳定性和准确性,来评估模型的表现。一些常用的评估方法包括均方误差(MSE)、平均绝对误差(MAE)、Akaike信息准则(AIC)等。
-
应用与解释:根据模型的预测结果做出决策或解释结果,例如制定业务策略、调整生产计划、投资决策等。
时间序列分析的常见方法:
-
平稳时间序列分析:假设时间序列的统计性质不随时间变化,主要适用于没有明显趋势和季节性波动的数据。
-
非平稳时间序列分析:针对存在趋势、季节性或其他非平稳特征的数据,通过差分、对数变换等方法将其转化为平稳序列进行分析。
-
指数平滑法:通过加权平均过去的观察值,对未来进行平滑预测,适用于带有季节性波动或趋势的时间序列。
-
周期性和季节性分析:识别和建模数据中的周期性和季节性成分,以更准确地预测未来的变化。
简单来说时间序列研究包含2个问题:
1.数据描述:这段时间已经发生了什么
2.预测数据:接下来要发生什么
将要用到的数据集
| 时间序列 | 描述 |
|---|---|
| AirPassengers | 1949-1960每月乘坐飞机的乘客数 |
| JohnsonJohnson | Johnson&Johnson每股季度收入 |
| nhtemp | 康涅狄格州纽黑文化区从1912年至1971年每年的平均气温 |
| Nile | 尼罗河流量 |
| sunspots | 1749-1983年月均太阳黑子数 |
需要用到的包
xts、forecast、tseries和directlabels,需要提前安装
14.1 数据描述
14.1.1 在R中生成时序对象
在R中分析时序对象的前提 是将分析对象转成时间序列对象,即R中一种包括观测值及其日期标记的数据结构。
用于储存时序数据的对象:

14.1.1.1 语法
library(xts)
myseries <- xts(data,index)data代表数据,它是一个向量、矩阵或数据框,包含要创建时间序列的数值数据。
index代表索引,它是一个日期时间向量,用于标识数据点的时间顺序。
14.1.1.2 举例
library(xts)
## Warning: 程辑包'xts'是用R版本4.3.2 来建造的
##
## ######################### Warning from 'xts' package ##########################
## # #
## # The dplyr lag() function breaks how base R's lag() function is supposed to #
## # work, which breaks lag(my_xts). Calls to lag(my_xts) that you type or #
## # source() into this session won't work correctly. #
## # #
## # Use stats::lag() to make sure you're not using dplyr::lag(), or you can add #
## # conflictRules('dplyr', exclude = 'lag') to your .Rprofile to stop #
## # dplyr from breaking base R's lag() function. #
## # #
## # Code in packages is not affected. It's protected by R's namespace mechanism #
## # Set `options(xts.warn_dplyr_breaks_lag = FALSE)` to suppress this warning. #
## # #
## ###############################################################################
##
## 载入程辑包:'xts'
## The following objects are masked from 'package:pastecs':
##
## first, last
## The following objects are masked from 'package:dplyr':
##
## first, last
sales <- c(18,33,22,4,23,44,55,12,22,30,11,52,
34,22,21,56,8,33,45,21,33,67,32,20)
date <- seq(from=as.Date("2018/1/1"),
to=as.Date("2019/12/1"),
by="month")
sale.xts <- xts(sales,date)
sale.xts
## [,1]
## 2018-01-01 18
## 2018-02-01 33
## 2018-03-01 22
## 2018-04-01 4
## 2018-05-01 23
## 2018-06-01 44
## 2018-07-01 55
## 2018-08-01 12
## 2018-09-01 22
## 2018-10-01 30
## 2018-11-01 11
## 2018-12-01 52
## 2019-01-01 34
## 2019-02-01 22
## 2019-03-01 21
## 2019-04-01 56
## 2019-05-01 8
## 2019-06-01 33
## 2019-07-01 45
## 2019-08-01 21
## 2019-09-01 33
## 2019-10-01 67
## 2019-11-01 32
## 2019-12-01 2014.1.1.3 xts格式设置子集
用[""]设定子集,例如:
sale.xts["2018-5"]
## [,1]
## 2018-05-01 23
sale.xts["2018-12/2019-3"]
## [,1]
## 2018-12-01 52
## 2019-01-01 34
## 2019-02-01 22
## 2019-03-01 2114.1.1.4 配合apply()函数对时间序列对象的每个时间段执行一个函数
语法:
newseries <- apply.period(x,FUN,...)period:一般设置为daily,weekly,monthly,quarterly,yearly
x:一个xts时间序列对象
FUN:要应用的函数
**举例:**计算sale.xts数据集每个季度的销售总量
library(xts)
new.sale.xts <- apply.quarterly(sale.xts,FUN=sum)
## Error in get(as.character(FUN), mode = "function", envir = envir): 没有状态为"function"的"FUN"目标对象
new.sale.xts
## Error in eval(expr, envir, enclos): 找不到对象'new.sale.xts'14.1.1.5 绘制时间序列图(forecast包中的autoplot()函数)
forecast包中的autoplot()函数可将时序数据绘制为ggplot2图形
默认图形:
library(forecast)
## Warning: 程辑包'forecast'是用R版本4.3.2 来建造的
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
library(ggplot2)
autoplot(sale.xts)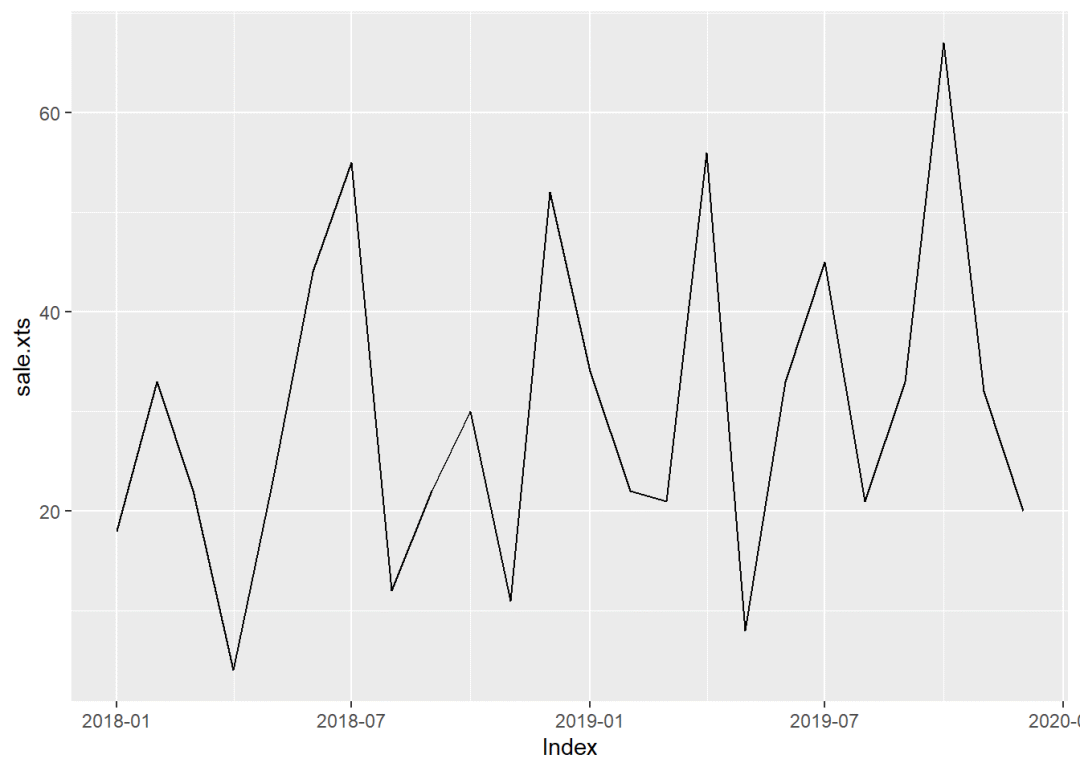
设置颜色和x轴标签及主题:
library(forecast)
library(ggplot2)
autoplot(sale.xts)+
geom_line(color="blue")+
scale_x_date(date_breaks="1 months",
date_labels="%b %y")+
labs(x="",y="Sales",title = "Customized Time Series Plot")+
theme_bw()+
theme(axis.text.x = element_text(angle = 90,vjust = 0.5,hjust = 1),
panel.grid.minor = element_blank())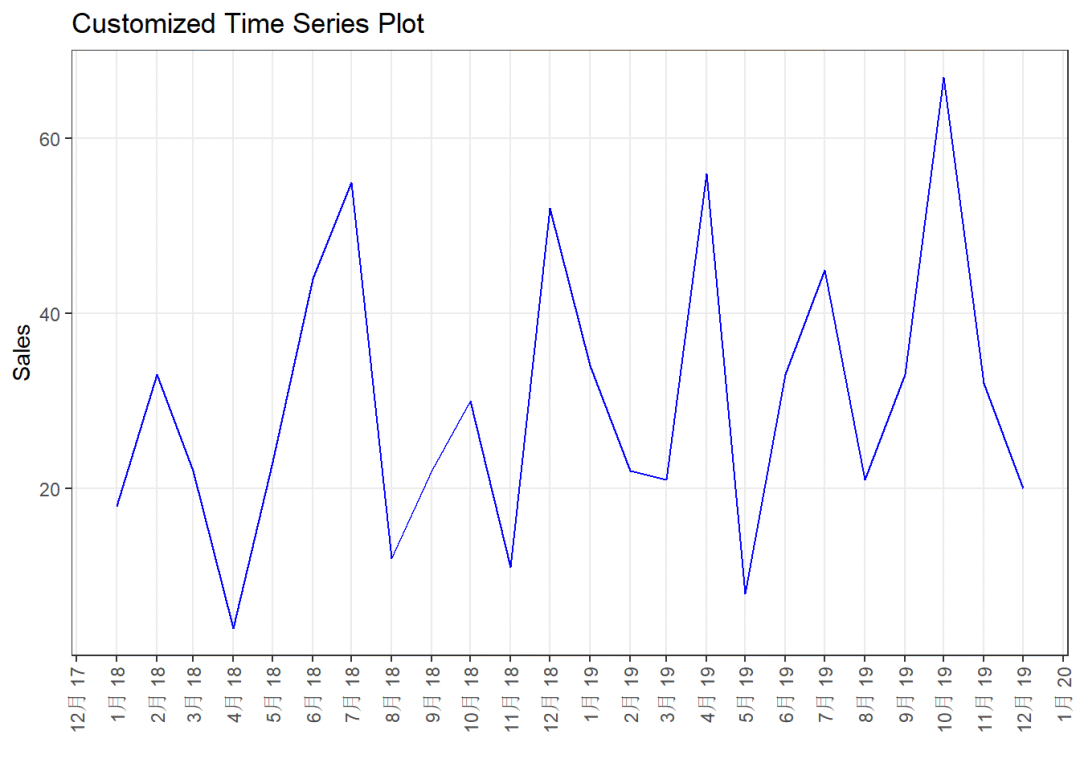
14.2 时序的平滑化和季度项分解
对时序数据建立复杂模型之前需要对其进行描述和可视化。
-
首先,可以对时序数据进行平滑化来探究总体趋势
-
并对其进行分解以观察时序列中是否存在季节项(如果存在明显的重复模式,可能表明存在季节性。)。
由于有时数据图片看不明显,可以利用平滑处理帮助我们将趋势看的更直接一些。
14.2.1 通过简单移动平均进行平滑处理
14.2.1.1 概念和语法
例如每个数据点都可以用这一点和其前后2个点的平均值来表示,这就是居中移动平均。k=2q+1,k一般设置为奇数。k值越大,越平滑。
(可以这样理解:假设k=3,则可以理解为数值n1,n2,n3变成(n1+n2)/2)
进行简单移动平均的函数:
TTR包中的SMA()函数,zoo包中的rollmean(),forecast包中的ma()函数。
ma()函数语法:
library(forecast)
ma(x,k)x:时序数据
k:每次用来平均的观测值的个数,奇数,k越大,越平滑。
通常,一开始并不知道应该将k设置为多少,为防止过平滑和欠平滑,可以多设置几个再从中选择最适合的。
14.2.1.2 举例
以Nile数据集为例
library(forecast)
library(ggplot2)
theme_set(theme_bw())
ylim <- c(min(Nile),max(Nile))#将Nile最小和最大值设置为ylim
autoplot(Nile)+
scale_y_continuous(limits = ylim)+#保证纵坐标的范围均为Nile最小到最大值
ggtitle("Row")#在ggplot2中设置标题用ggtitle()函数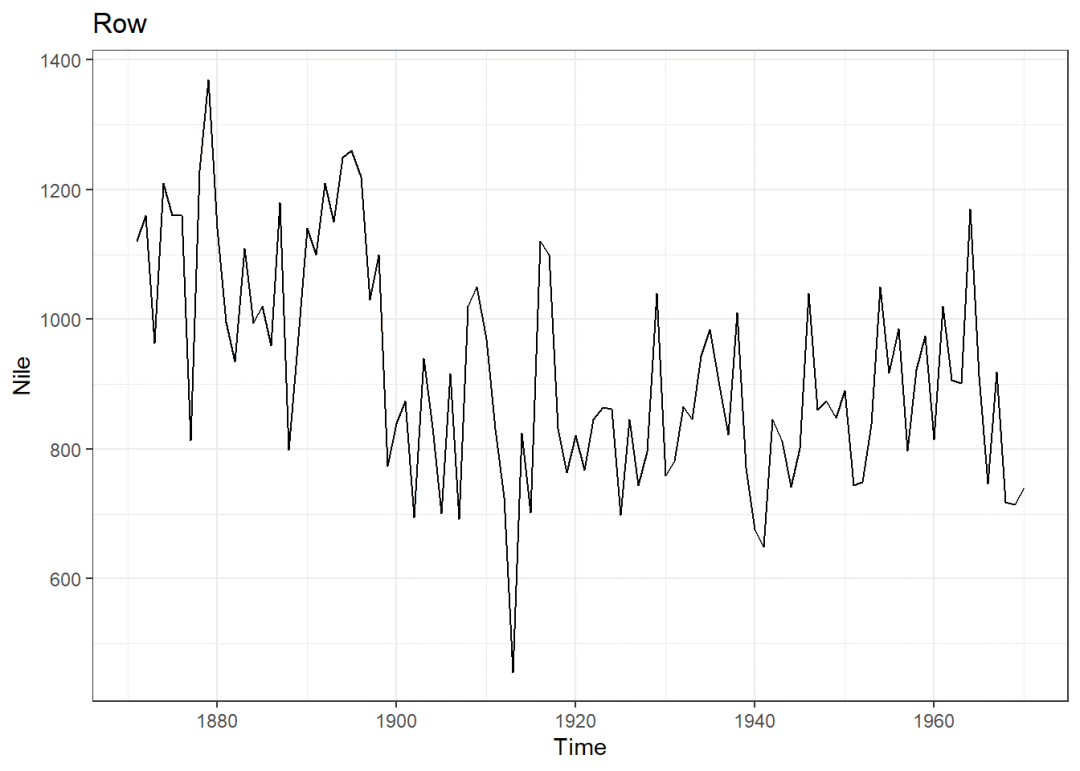
autoplot(ma(Nile,3))+
ggtitle("k=3")+
scale_y_continuous(limits = ylim)
autoplot(ma(Nile,7))+
ggtitle("k=7")+
scale_y_continuous(limits = ylim)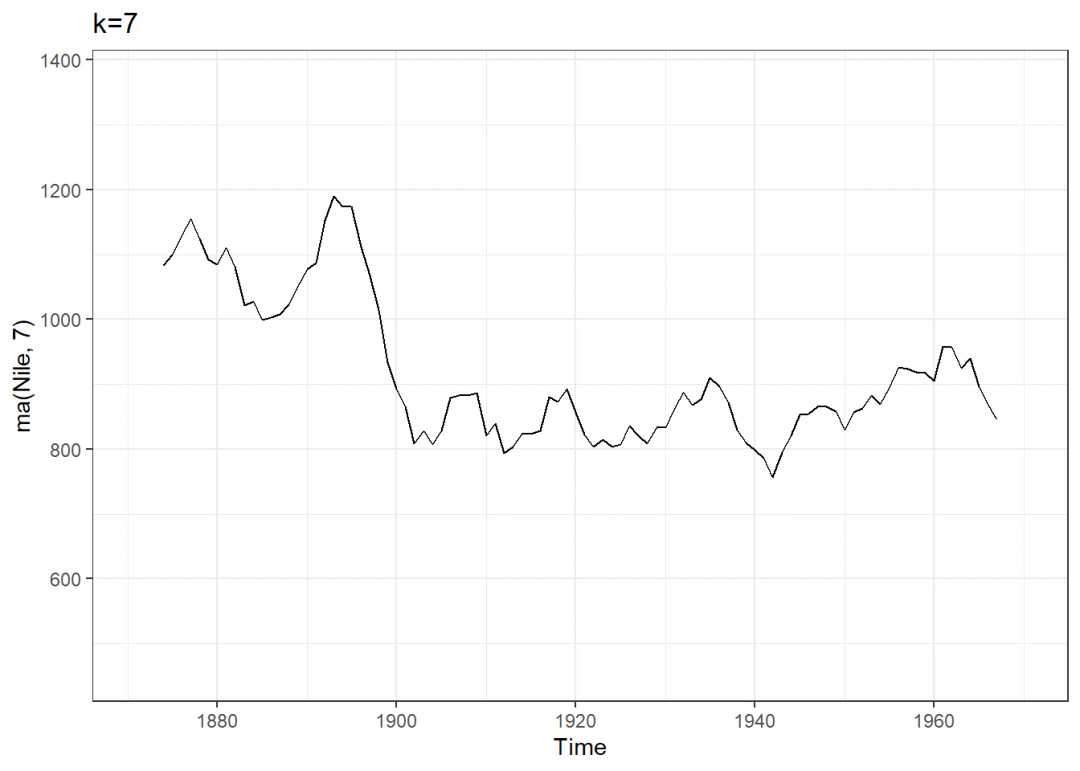
autoplot(ma(Nile,15))+
ggtitle("k=15")+
scale_y_continuous(limits = ylim)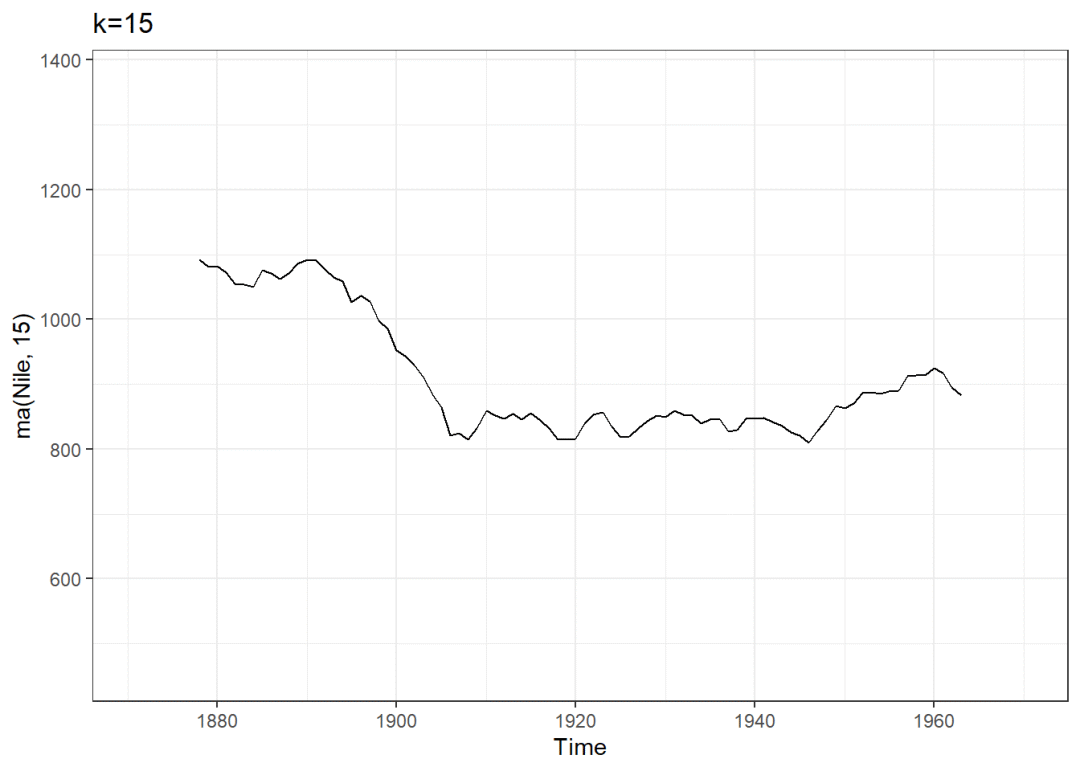
结果显示:k=15时,数据趋势最平滑。
当存在季节项时,则需要进行季节项处理。
14.2.2 季节项分解
如何判定有没有季节项呢?反复研究和阅读比较P329的图15-5即可以从中找出规律。
区分相加模型和相乘模型:
相乘模型:序列的波动是与趋势成正比的,即整体增长时波动增强(幅度会变大);
相加模型:波动不会随趋势增加而增强
两种模型的相互转化:
相加模型=log(相乘模型)
相乘模型=exp(相加模型)
14.2.2.1 语法
1.stats包(内置包)中stl()函数。注意该函数仅用于相加模型,可以将相乘模型转化为相加模型后再使用。
stl(ts,s.window = ,t.window = )ts:将要分解的时序(必填项)
"s.window"是用于季节性分解的窗口大小,必填项,默认为"periodic",表示使用周期性窗口进行季节性分解。(必填项)
"t.window"是用于趋势分解的窗口大小。默认为NULL,表示不使用窗口对趋势进行分解。
2.fit$time.series
stl()函数返回的对象中有一项是time.series,它包括每个观测值中的各分解项------趋势项、季节项以及随机项的值。可以通过exp(fit$time.series)将结果转化为原始尺度(相加转回相乘):
fit$time.series
exp(fit$time.series)14.2.2.2 举例
数据集:AirPassengers
library(forecast)
library(ggplot2)
autoplot(AirPassengers)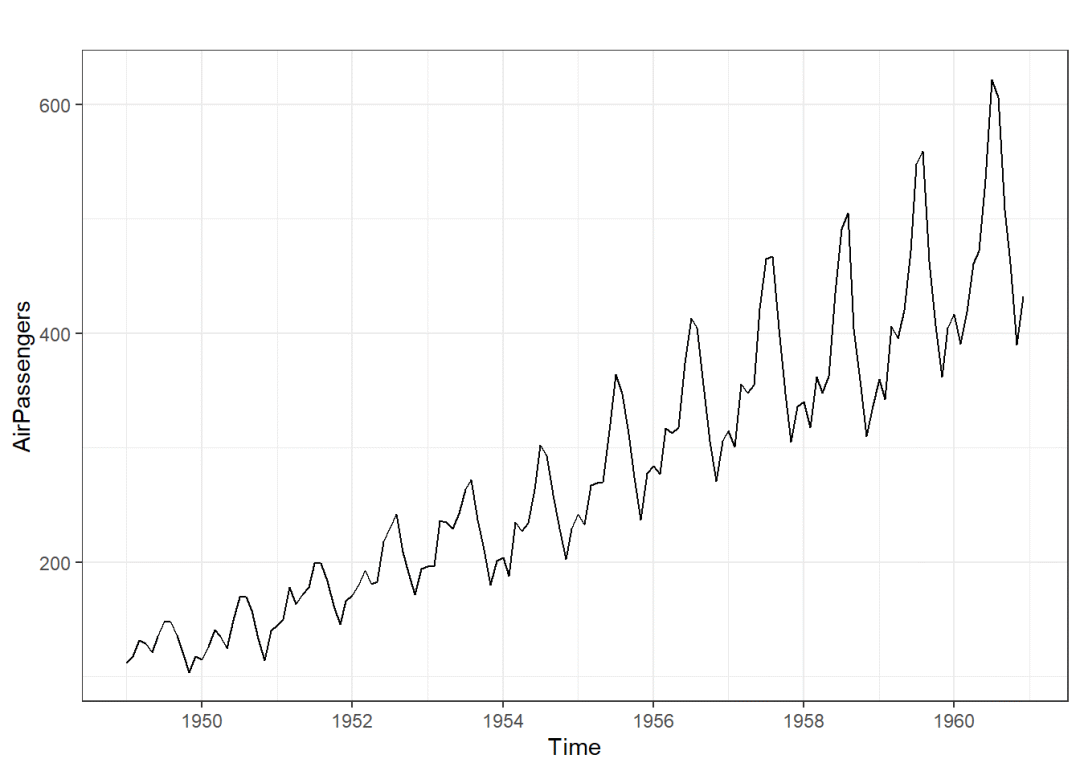
从图上可以看出是一个相乘模型,由于stl()函数仅处理相加模型,因此需要转化为相加模型:
AirPassengers1 <- log(AirPassengers)
autoplot(AirPassengers1)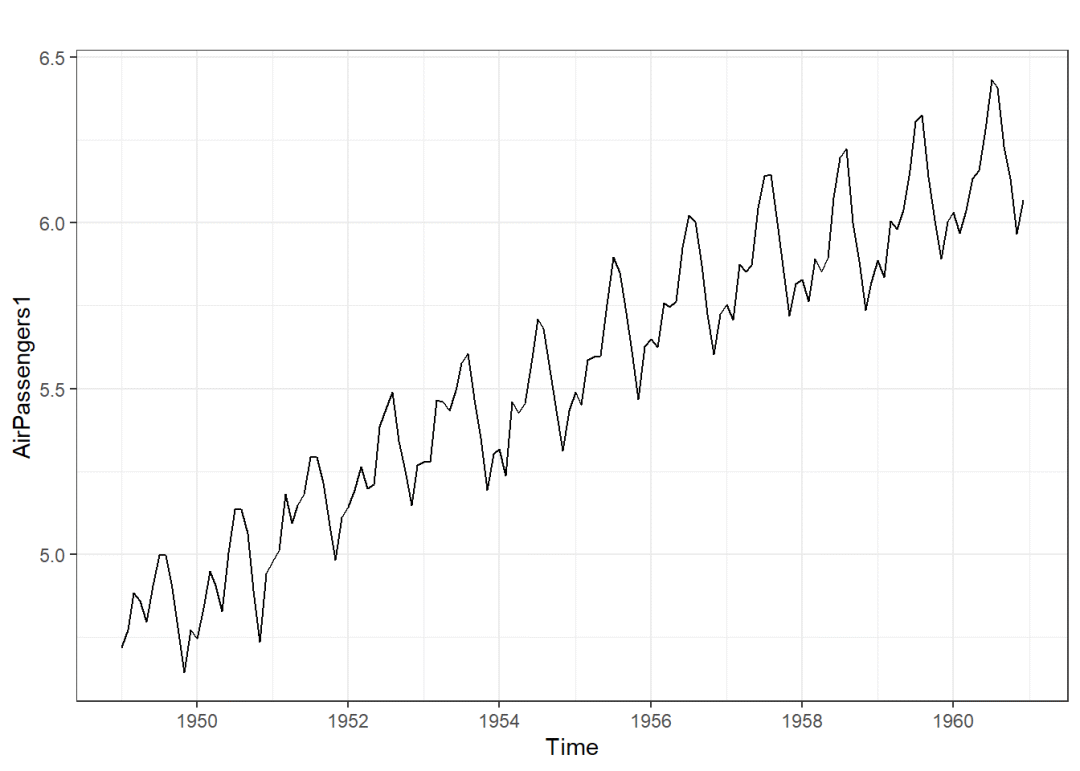
接着进行stl()处理进行季节项分解
fit <- stl(AirPassengers1,s.window = "periodic")
autoplot(fit)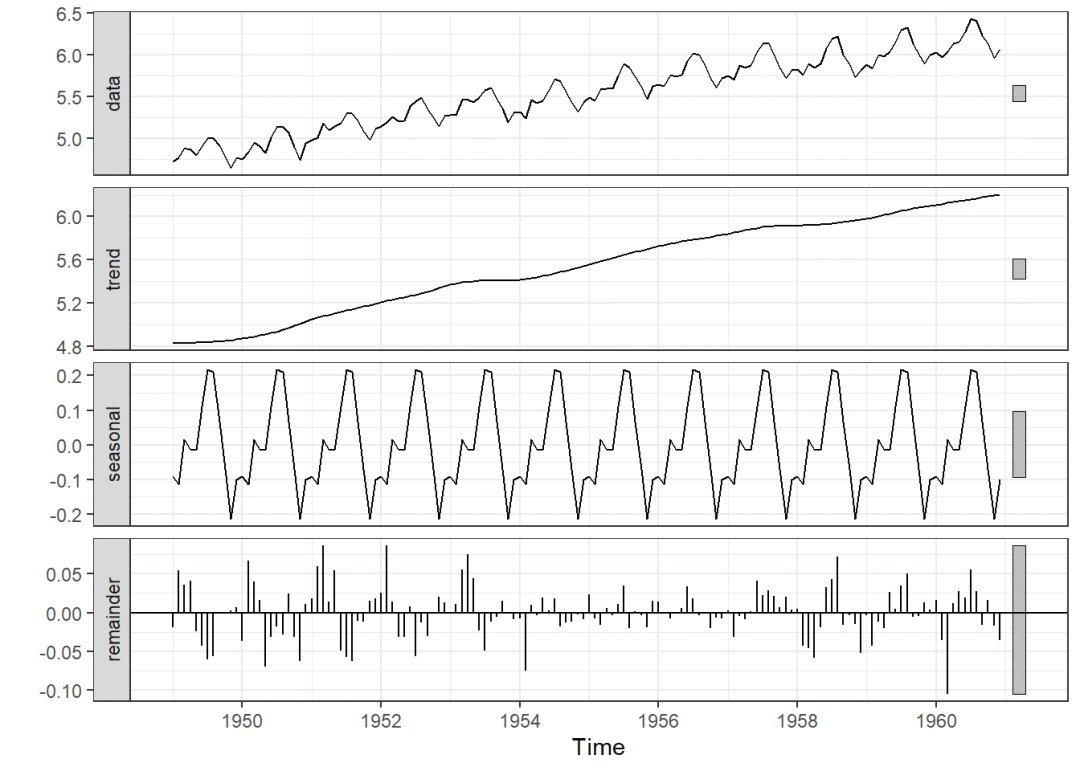
将各趋势项的值转化为原始尺度:
fit$time.series
## seasonal trend remainder
## Jan 1949 -0.09164042 4.829389 -0.0192493585
## Feb 1949 -0.11402828 4.830368 0.0543447685
## Mar 1949 0.01586585 4.831348 0.0355884457
## Apr 1949 -0.01402759 4.833377 0.0404632511
## May 1949 -0.01502478 4.835406 -0.0245905300
## Jun 1949 0.10978976 4.838166 -0.0426814256
## Jul 1949 0.21640041 4.840927 -0.0601151688
## Aug 1949 0.20960587 4.843469 -0.0558624690
## Sep 1949 0.06747156 4.846011 -0.0008273977
## Oct 1949 -0.07024836 4.850883 -0.0015112948
## Nov 1949 -0.21352774 4.855756 0.0021630667
## Dec 1949 -0.10063625 4.864586 0.0067346600
## Jan 1950 -0.09164042 4.873417 -0.0368443057
## Feb 1950 -0.11402828 4.883282 0.0670284530
## Mar 1950 0.01586585 4.893147 0.0397474219
## Apr 1950 -0.01402759 4.903156 0.0161459950
## May 1950 -0.01502478 4.913166 -0.0698276070
## Jun 1950 0.10978976 4.925404 -0.0312477713
## Jul 1950 0.21640041 4.937643 -0.0182444833
## Aug 1950 0.20960587 4.954420 -0.0282273969
## Sep 1950 0.06747156 4.971197 0.0239260449
## Oct 1950 -0.07024836 4.991662 -0.0310647612
## Nov 1950 -0.21352774 5.012127 -0.0624008823
## Dec 1950 -0.10063625 5.031094 0.0111846224
## Jan 1951 -0.09164042 5.050061 0.0183131352
## Feb 1951 -0.11402828 5.065044 0.0596196836
## Mar 1951 0.01586585 5.080027 0.0858909418
## Apr 1951 -0.01402759 5.093932 0.0138460280
## May 1951 -0.01502478 5.107837 0.0546824937
## Jun 1951 0.10978976 5.121064 -0.0490698826
## Jul 1951 0.21640041 5.134291 -0.0573861680
## Aug 1951 0.20960587 5.146131 -0.0624323009
## Sep 1951 0.06747156 5.157972 -0.0105077415
## Oct 1951 -0.07024836 5.169854 -0.0120089320
## Nov 1951 -0.21352774 5.181735 0.0153990463
## Dec 1951 -0.10063625 5.194803 0.0178207135
## Jan 1952 -0.09164042 5.207871 0.0254326447
## Feb 1952 -0.11402828 5.220493 0.0864920261
## Mar 1952 0.01586585 5.233115 0.0137094563
## Apr 1952 -0.01402759 5.244400 -0.0318757882
## May 1952 -0.01502478 5.255686 -0.0311749995
## Jun 1952 0.10978976 5.266916 0.0077889001
## Jul 1952 0.21640041 5.278147 -0.0564679741
## Aug 1952 0.20960587 5.291899 -0.0125671875
## Sep 1952 0.06747156 5.305651 -0.0307885329
## Oct 1952 -0.07024836 5.323035 -0.0005129219
## Nov 1952 -0.21352774 5.340418 0.0206040218
## Dec 1952 -0.10063625 5.355790 0.0127045234
## Jan 1953 -0.09164042 5.371162 -0.0014064946
## Feb 1953 -0.11402828 5.381701 0.0104415885
## Mar 1953 0.01586585 5.392241 0.0557248228
## Apr 1953 -0.01402759 5.398479 0.0751345805
## May 1953 -0.01502478 5.404716 0.0440308724
## Jun 1953 0.10978976 5.406792 -0.0235205660
## Jul 1953 0.21640041 5.408869 -0.0493198945
## Aug 1953 0.20960587 5.407808 -0.0116118099
## Sep 1953 0.06747156 5.406747 -0.0061588541
## Oct 1953 -0.07024836 5.407020 0.0150868577
## Nov 1953 -0.21352774 5.407292 -0.0008072455
## Dec 1953 -0.10063625 5.412628 -0.0086865700
## Jan 1954 -0.09164042 5.417964 -0.0082032035
## Feb 1954 -0.11402828 5.425823 -0.0753528534
## Mar 1954 0.01586585 5.433683 0.0100370842
## Apr 1954 -0.01402759 5.442676 -0.0036988730
## May 1954 -0.01502478 5.451670 0.0186755182
## Jun 1954 0.10978976 5.463574 0.0025856037
## Jul 1954 0.21640041 5.475477 0.0185495056
## Aug 1954 0.20960587 5.488954 -0.0183873611
## Sep 1954 0.06747156 5.502431 -0.0130746073
## Oct 1954 -0.07024836 5.515678 -0.0117077856
## Nov 1954 -0.21352774 5.528925 -0.0021914704
## Dec 1954 -0.10063625 5.543178 -0.0088199260
## Jan 1955 -0.09164042 5.557431 0.0231469788
## Feb 1955 -0.11402828 5.572621 -0.0075538774
## Mar 1955 0.01586585 5.587810 -0.0164272509
## Apr 1955 -0.01402759 5.602576 0.0061625730
## May 1955 -0.01502478 5.617343 -0.0038959909
## Jun 1955 0.10978976 5.631685 0.0110981305
## Jul 1955 0.21640041 5.646027 0.0347266908
## Aug 1955 0.20960587 5.660026 -0.0203074185
## Sep 1955 0.06747156 5.674026 0.0015057273
## Oct 1955 -0.07024836 5.687411 -0.0040342159
## Nov 1955 -0.21352774 5.700795 -0.0192075831
## Dec 1955 -0.10063625 5.713683 0.0145740752
## Jan 1956 -0.09164042 5.726571 0.0140435478
## Feb 1956 -0.11402828 5.738688 -0.0006422520
## Mar 1956 0.01586585 5.750805 -0.0077690470
## Apr 1956 -0.01402759 5.761271 -0.0010403672
## May 1956 -0.01502478 5.771737 0.0053388421
## Jun 1956 0.10978976 5.780581 0.0338845974
## Jul 1956 0.21640041 5.789426 0.0176216235
## Aug 1956 0.20960587 5.797448 -0.0031667752
## Sep 1956 0.06747156 5.805470 -0.0008241663
## Oct 1956 -0.07024836 5.813734 -0.0199006689
## Nov 1956 -0.21352774 5.821998 -0.0063513051
## Dec 1956 -0.10063625 5.831654 -0.0074325201
## Jan 1957 -0.09164042 5.841310 0.0029031831
## Feb 1957 -0.11402828 5.852625 -0.0314869189
## Mar 1957 0.01586585 5.863941 -0.0048761755
## Apr 1957 -0.01402759 5.875005 -0.0087747176
## May 1957 -0.01502478 5.886069 0.0010740550
## Jun 1957 0.10978976 5.894711 0.0405045167
## Jul 1957 0.21640041 5.903354 0.0222834352
## Aug 1957 0.20960587 5.907786 0.0289376116
## Sep 1957 0.06747156 5.912218 0.0217253156
## Oct 1957 -0.07024836 5.912909 0.0066639927
## Nov 1957 -0.21352774 5.913600 0.0202392244
## Dec 1957 -0.10063625 5.914570 0.0031777723
## Jan 1958 -0.09164042 5.915539 0.0050470568
## Feb 1958 -0.11402828 5.918512 -0.0424324225
## Mar 1958 0.01586585 5.921485 -0.0457068326
## Apr 1958 -0.01402759 5.924977 -0.0587474166
## May 1958 -0.01502478 5.928470 -0.0190421600
## Jun 1958 0.10978976 5.932704 0.0328523706
## Jul 1958 0.21640041 5.936938 0.0431056910
## Aug 1958 0.20960587 5.943328 0.0716243517
## Sep 1958 0.06747156 5.949718 -0.0157750808
## Oct 1958 -0.07024836 5.957409 -0.0038387222
## Nov 1958 -0.21352774 5.965101 -0.0150005051
## Dec 1958 -0.10063625 5.973333 -0.0526139823
## Jan 1959 -0.09164042 5.981566 -0.0038213288
## Feb 1959 -0.11402828 5.992040 -0.0432006658
## Mar 1959 0.01586585 6.002514 -0.0120262807
## Apr 1959 -0.01402759 6.015640 -0.0201986959
## May 1959 -0.01502478 6.028767 0.0265120912
## Jun 1959 0.10978976 6.042198 0.0049914005
## Jul 1959 0.21640041 6.055628 0.0342466268
## Aug 1959 0.20960587 6.065881 0.0506625860
## Sep 1959 0.06747156 6.076134 -0.0058783006
## Oct 1959 -0.07024836 6.084145 -0.0050832771
## Nov 1959 -0.21352774 6.092156 0.0130161013
## Dec 1959 -0.10063625 6.100500 0.0040231864
## Jan 1960 -0.09164042 6.108844 0.0158822334
## Feb 1960 -0.11402828 6.117934 -0.0351985510
## Mar 1960 0.01586585 6.127024 -0.1050193083
## Apr 1960 -0.01402759 6.135814 0.0116112609
## May 1960 -0.01502478 6.144604 0.0273994037
## Jun 1960 0.10978976 6.152986 0.0194908174
## Jul 1960 0.21640041 6.161368 0.0551717057
## Aug 1960 0.20960587 6.170124 0.0271500533
## Sep 1960 0.06747156 6.178880 -0.0158702714
## Oct 1960 -0.07024836 6.187594 0.0160525773
## Nov 1960 -0.21352774 6.196307 -0.0166330133
## Dec 1960 -0.10063625 6.204752 -0.0356905175
exp(fit$time.series)
## seasonal trend remainder
## Jan 1949 0.9124332 125.1344 0.9809347
## Feb 1949 0.8922327 125.2571 1.0558486
## Mar 1949 1.0159924 125.3798 1.0362293
## Apr 1949 0.9860703 125.6345 1.0412930
## May 1949 0.9850875 125.8897 0.9757094
## Jun 1949 1.1160434 126.2377 0.9582166
## Jul 1949 1.2415994 126.5866 0.9416561
## Aug 1949 1.2331919 126.9088 0.9456692
## Sep 1949 1.0697998 127.2318 0.9991729
## Oct 1949 0.9321623 127.8533 0.9984898
## Nov 1949 0.8077298 128.4777 1.0021654
## Dec 1949 0.9042619 129.6173 1.0067574
## Jan 1950 0.9124332 130.7670 0.9638262
## Feb 1950 0.8922327 132.0634 1.0693259
## Mar 1950 1.0159924 133.3726 1.0405479
## Apr 1950 0.9860703 134.7143 1.0162770
## May 1950 0.9850875 136.0695 0.9325546
## Jun 1950 1.1160434 137.7450 0.9692354
## Jul 1950 1.2415994 139.4411 0.9819209
## Aug 1950 1.2331919 141.8003 0.9721673
## Sep 1950 1.0697998 144.1995 1.0242146
## Oct 1950 0.9321623 147.1809 0.9694128
## Nov 1950 0.8077298 150.2239 0.9395062
## Dec 1950 0.9042619 153.1004 1.0112474
## Jan 1951 0.9124332 156.0320 1.0184818
## Feb 1951 0.8922327 158.3874 1.0614328
## Mar 1951 1.0159924 160.7784 1.0896875
## Apr 1951 0.9860703 163.0296 1.0139423
## May 1951 0.9850875 165.3124 1.0562052
## Jun 1951 1.1160434 167.5135 0.9521146
## Jul 1951 1.2415994 169.7439 0.9442294
## Aug 1951 1.2331919 171.7657 0.9394767
## Sep 1951 1.0697998 173.8116 0.9895473
## Oct 1951 0.9321623 175.8891 0.9880629
## Nov 1951 0.8077298 177.9914 1.0155182
## Dec 1951 0.9042619 180.3327 1.0179804
## Jan 1952 0.9124332 182.7047 1.0257588
## Feb 1952 0.8922327 185.0254 1.0903427
## Mar 1952 1.0159924 187.3755 1.0138039
## Apr 1952 0.9860703 189.5022 0.9686269
## May 1952 0.9850875 191.6529 0.9693059
## Jun 1952 1.1160434 193.8174 1.0078193
## Jul 1952 1.2415994 196.0063 0.9450968
## Aug 1952 1.2331919 198.7204 0.9875114
## Sep 1952 1.0697998 201.4722 0.9696806
## Oct 1952 0.9321623 205.0051 0.9994872
## Nov 1952 0.8077298 208.5999 1.0208178
## Dec 1952 0.9042619 211.8312 1.0127856
## Jan 1953 0.9124332 215.1126 0.9985945
## Feb 1953 0.8922327 217.3918 1.0104963
## Mar 1953 1.0159924 219.6952 1.0573067
## Apr 1953 0.9860703 221.0698 1.0780292
## May 1953 0.9850875 222.4530 1.0450146
## Jun 1953 1.1160434 222.9154 0.9767539
## Jul 1953 1.2415994 223.3787 0.9518766
## Aug 1953 1.2331919 223.1419 0.9884553
## Sep 1953 1.0697998 222.9054 0.9938601
## Oct 1953 0.9321623 222.9661 1.0152012
## Nov 1953 0.8077298 223.0268 0.9991931
## Dec 1953 0.9042619 224.2200 0.9913510
## Jan 1954 0.9124332 225.4196 0.9918304
## Feb 1954 0.8922327 227.1983 0.9274162
## Mar 1954 1.0159924 228.9910 1.0100876
## Apr 1954 0.9860703 231.0598 0.9963080
## May 1954 0.9850875 233.1473 1.0188510
## Jun 1954 1.1160434 235.9391 1.0025889
## Jul 1954 1.2415994 238.7644 1.0187226
## Aug 1954 1.2331919 242.0040 0.9817807
## Sep 1954 1.0697998 245.2875 0.9870105
## Oct 1954 0.9321623 248.5585 0.9883605
## Nov 1954 0.8077298 251.8730 0.9978109
## Dec 1954 0.9042619 255.4887 0.9912189
## Jan 1955 0.9124332 259.1563 1.0234169
## Feb 1955 0.8922327 263.1227 0.9924746
## Mar 1955 1.0159924 267.1499 0.9837069
## Apr 1955 0.9860703 271.1240 1.0061816
## May 1955 0.9850875 275.1572 0.9961116
## Jun 1955 1.1160434 279.1320 1.0111599
## Jul 1955 1.2415994 283.1642 1.0353367
## Aug 1955 1.2331919 287.1562 0.9798974
## Sep 1955 1.0697998 291.2045 1.0015069
## Oct 1955 0.9321623 295.1284 0.9959739
## Nov 1955 0.8077298 299.1052 0.9809757
## Dec 1955 0.9042619 302.9850 1.0146808
## Jan 1956 0.9124332 306.9151 1.0141426
## Feb 1956 0.8922327 310.6566 0.9993580
## Mar 1956 1.0159924 314.4437 0.9922611
## Apr 1956 0.9860703 317.7520 0.9989602
## May 1956 0.9850875 321.0951 1.0053531
## Jun 1956 1.1160434 323.9475 1.0344652
## Jul 1956 1.2415994 326.8252 1.0177778
## Aug 1956 1.2331919 329.4577 0.9968382
## Sep 1956 1.0697998 332.1114 0.9991762
## Oct 1956 0.9321623 334.8672 0.9802960
## Nov 1956 0.8077298 337.6460 0.9936688
## Dec 1956 0.9042619 340.9221 0.9925950
## Jan 1957 0.9124332 344.2299 1.0029074
## Feb 1957 0.8922327 348.1472 0.9690036
## Mar 1957 1.0159924 352.1091 0.9951357
## Apr 1957 0.9860703 356.0264 0.9912637
## May 1957 0.9850875 359.9872 1.0010746
## Jun 1957 1.1160434 363.1119 1.0413360
## Jul 1957 1.2415994 366.2637 1.0225336
## Aug 1957 1.2331919 367.8907 1.0293604
## Sep 1957 1.0697998 369.5249 1.0219630
## Oct 1957 0.9321623 369.7803 1.0066862
## Nov 1957 0.8077298 370.0360 1.0204454
## Dec 1957 0.9042619 370.3949 1.0031828
## Jan 1958 0.9124332 370.7541 1.0050598
## Feb 1958 0.8922327 371.8580 0.9584552
## Mar 1958 1.0159924 372.9652 0.9553220
## Apr 1958 0.9860703 374.2700 0.9429449
## May 1958 0.9850875 375.5794 0.9811380
## Jun 1958 1.1160434 377.1730 1.0333980
## Jul 1958 1.2415994 378.7734 1.0440482
## Aug 1958 1.2331919 381.2015 1.0742517
## Sep 1958 1.0697998 383.6453 0.9843487
## Oct 1958 0.9321623 386.6073 0.9961686
## Nov 1958 0.8077298 389.5922 0.9851114
## Dec 1958 0.9042619 392.8128 0.9487462
## Jan 1959 0.9124332 396.0600 0.9961860
## Feb 1959 0.8922327 400.2301 0.9577192
## Mar 1959 1.0159924 404.4441 0.9880457
## Apr 1959 0.9860703 409.7882 0.9800039
## May 1959 0.9850875 415.2029 1.0268667
## Jun 1959 1.1160434 420.8169 1.0050039
## Jul 1959 1.2415994 426.5068 1.0348398
## Aug 1959 1.2331919 430.9021 1.0519679
## Sep 1959 1.0697998 435.3428 0.9941389
## Oct 1959 0.9321623 438.8444 0.9949296
## Nov 1959 0.8077298 442.3741 1.0131012
## Dec 1959 0.9042619 446.0808 1.0040313
## Jan 1960 0.9124332 449.8186 1.0160090
## Feb 1960 0.8922327 453.9261 0.9654137
## Mar 1960 1.0159924 458.0711 0.9003071
## Apr 1960 0.9860703 462.1153 1.0116789
## May 1960 0.9850875 466.1952 1.0277782
## Jun 1960 1.1160434 470.1191 1.0196820
## Jul 1960 1.2415994 474.0762 1.0567220
## Aug 1960 1.2331919 478.2454 1.0275220
## Sep 1960 1.0697998 482.4514 0.9842550
## Oct 1960 0.9321623 486.6737 1.0161821
## Nov 1960 0.8077298 490.9329 0.9835046
## Dec 1960 0.9042619 495.0963 0.964938914.3 数据预测
14.3.1 指数预测模型
分别有单指数模型、双指数模型和三指数模型
单指数模型:拟合的只有水平项和随机项
双指数模型(Holt指数平滑):包含水平项和趋势项
三指数模型(Holt-Winters):包含水平项、趋势项和季节项
14.3.1.1 语法
函数:forecast包中的ets()函数,model=随机项、趋势项、季节项(按顺序对应3个字母)
用于拟合指数模型的函数列表:
| 类型 | 参数 | 函数 |
|---|---|---|
| 单指数 | 水平项 | ets(ts,model="ANN") ses(ts) |
| 双指数 | 水平项、趋势项 | ets(ts,model="AAN") holt(ts) |
| 三指数 | 水平项、趋势项、季节项 | ets(ts,model="AAA") hw(ts) |
其中:A为相加模型,M为相乘模型,N为无,Z为自动选择。ses(ts) 、holt(ts)和hw(ts) 都是函数ets()的便捷包装。
选择用哪种函数是根据时序数据的特点来的。
fit <- est(ts,model=)#拟合模型
fit
forecast(fit,k)#k步向前预测,预测k个点
accuracy(fit)#输出准确度度量,看预测的准确性其中accuracy()函数也是forecast包提供,预测准确度度量表如下:

14.3.1.2 单指数函数
不含季节项和趋势项,只有水平项和随机项。
用数据集nhtemp(康涅狄格州纽黑文化区从1912年至1971年每年的平均气温)来举例,首先看一下它适合哪种函数:
autoplot(nhtemp)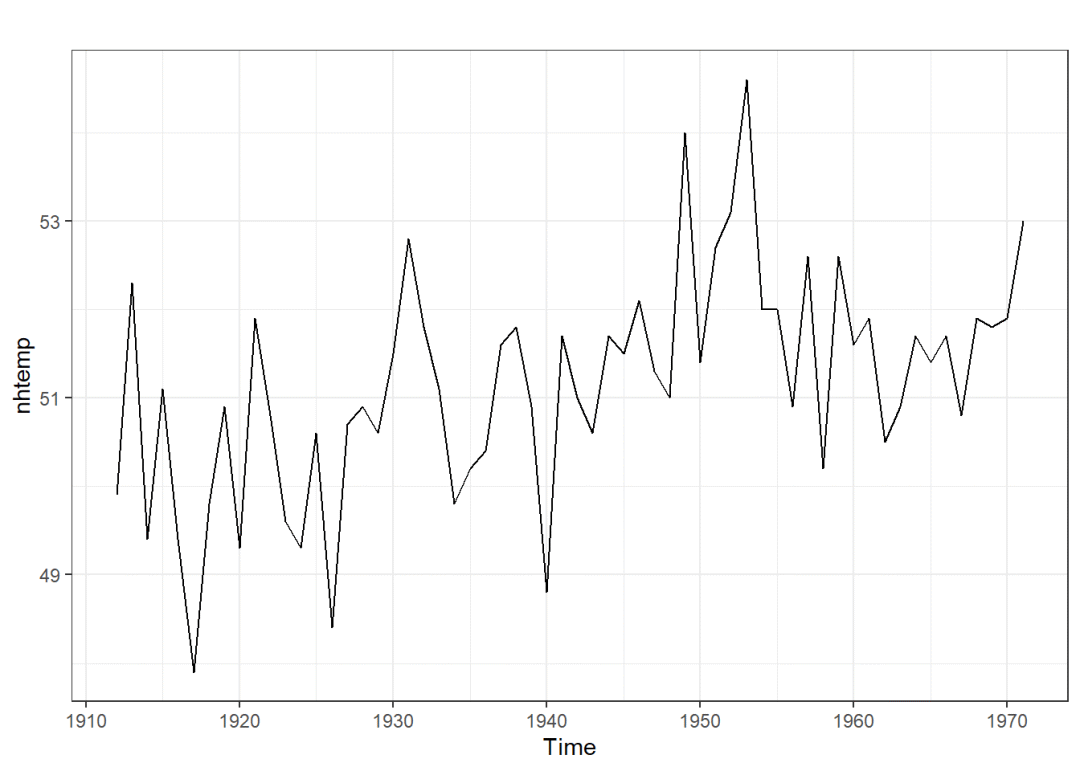
从图像上可以看到这个不存在趋势项和季节项,因此适用单指数模型:
library(forecast)
fit <- ets(nhtemp,model="ANN")
fit
## ETS(A,N,N)
##
## Call:
## ets(y = nhtemp, model = "ANN")
##
## Smoothing parameters:
## alpha = 0.1819
##
## Initial states:
## l = 50.2762
##
## sigma: 1.1455
##
## AIC AICc BIC
## 265.9298 266.3584 272.2129
fit1 <- forecast(fit,1)
autoplot(fit1)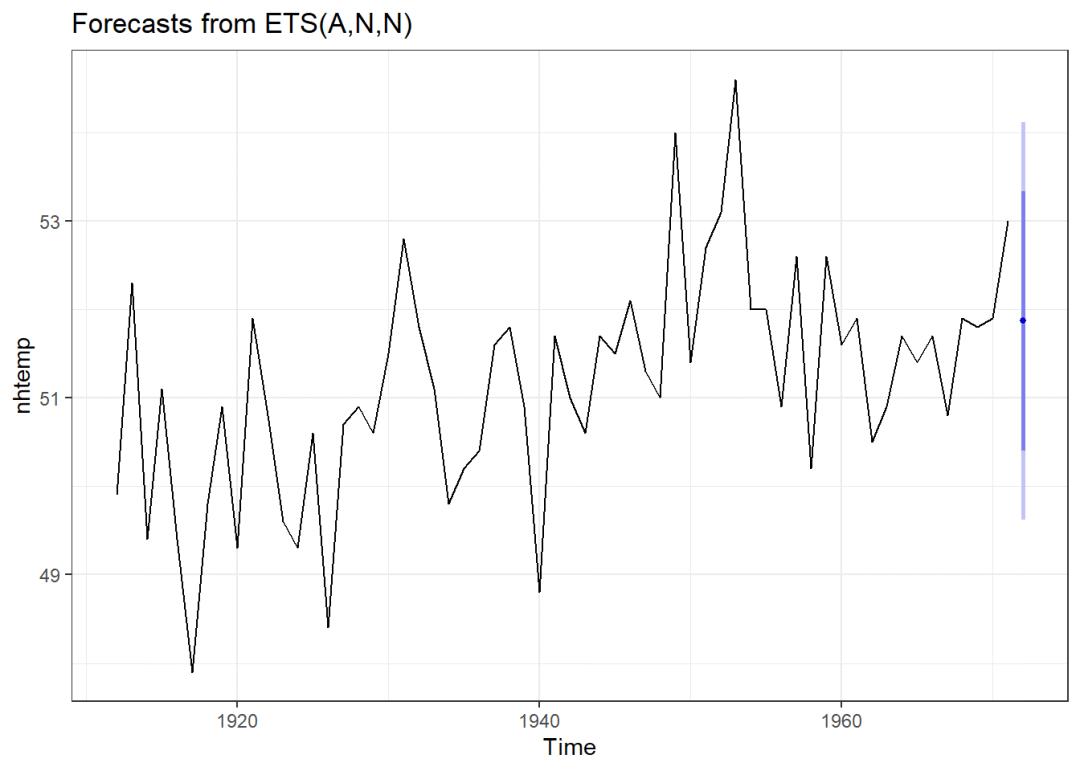
accuracy(fit)
## ME RMSE MAE MPE MAPE MASE
## Training set 0.1460657 1.126268 0.8951225 0.2419373 1.7489 0.7512408
## ACF1
## Training set -0.006441923注:alpha(α)控制着过去观测值对预测的权重。较小的alpha值表示更快的遗忘因子,更强调最近的观测值,而较大的alpha值则平衡了更多过去观测值的权重。
在ETS模型的结果中,返回的alpha值(例如,alpha = 0.1819)表示模型使用的平滑系数。在该特定模型中,alpha的值为0.1819,意味着较高的权重被赋予最近观测值,而较低的权重被赋予较早的观测值。
这个值可以帮助您理解模型对观测值的平滑程度和对最近观测值的敏感性。根据具体情况,您可以根据业务需求和模型性能来调整alpha的值。
14.3.1.3 Holt指数平滑(双指数)和Holt-Winters指数平滑(三指数)
以AirPassengers时序数据为例,图片显示出存在趋势项和季节项,且是相乘模型,适合Holt-Winters指数平滑
autoplot(AirPassengers)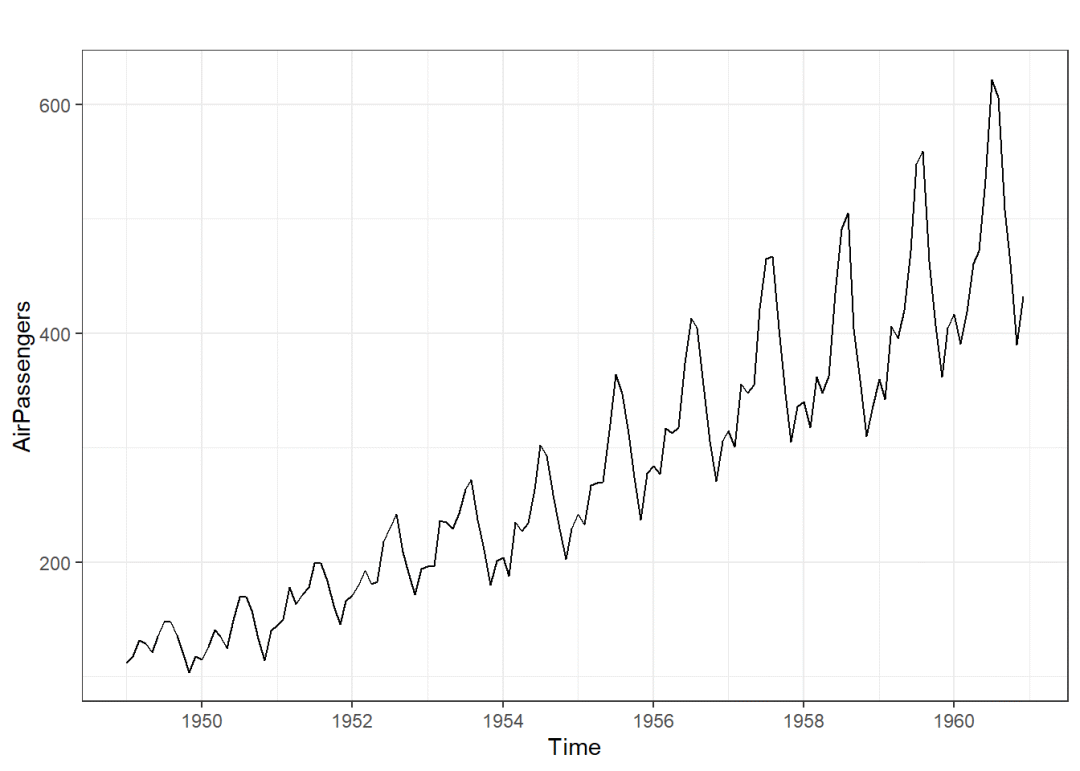
1)直接利用相乘模型预测MMM
fit <- ets(AirPassengers,model="MMM")
fit
## ETS(M,Md,M)
##
## Call:
## ets(y = AirPassengers, model = "MMM")
##
## Smoothing parameters:
## alpha = 0.7307
## beta = 0.0123
## gamma = 1e-04
## phi = 0.98
##
## Initial states:
## l = 120.9625
## b = 1.016
## s = 0.894 0.7968 0.9202 1.0581 1.2189 1.2312
## 1.1112 0.9807 0.9812 1.0133 0.8882 0.9063
##
## sigma: 0.0389
##
## AIC AICc BIC
## 1393.237 1398.709 1446.694
fit1 <- forecast(AirPassengers,5)
autoplot(fit1)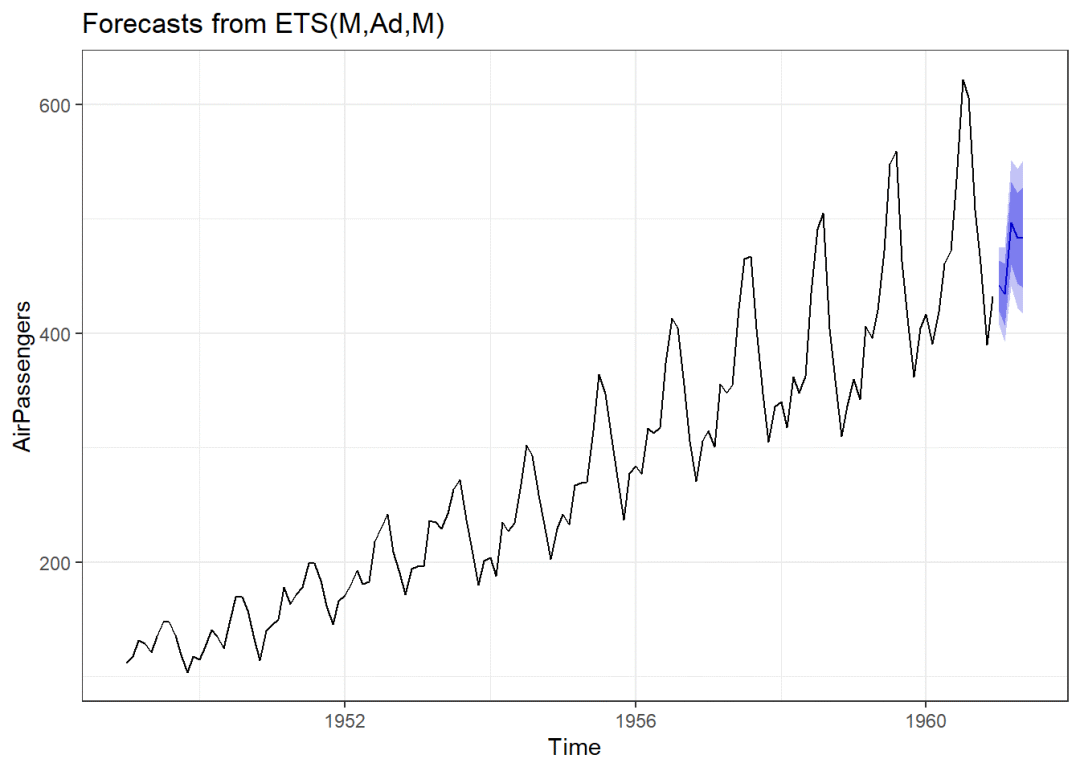
解读这三个值: alpha = 0.7307 ,平滑参数,控制水平项的指数下降。范围0-1,值越大意味着越近的观测值的权重越大;
beta = 0.0123 ,平滑参数,控制趋势项的指数下降。范围0-1,值越大意味着越近的观测值的权重越大;
gamma = 1e-04 ,平滑参数,控制季节项的指数下降。范围0-1,值越大意味着越近的观测值的权重越大(三指数模型才有)
2.1)转化为利用相加模型预测MMM
fit <- ets(log(AirPassengers),model="AAA")
fit
## ETS(A,A,A)
##
## Call:
## ets(y = log(AirPassengers), model = "AAA")
##
## Smoothing parameters:
## alpha = 0.6975
## beta = 0.0031
## gamma = 1e-04
##
## Initial states:
## l = 4.7925
## b = 0.0111
## s = -0.1045 -0.2206 -0.0787 0.0562 0.2049 0.2149
## 0.1146 -0.0081 -0.0059 0.0225 -0.1113 -0.0841
##
## sigma: 0.0383
##
## AIC AICc BIC
## -207.1694 -202.3123 -156.6826
fit1 <- forecast(AirPassengers,5)
autoplot(fit1)
2.2)利用exp()函数求出原始尺度
fit1$mean <- exp(fit1$mean)
fit1$lower <- exp(fit1$lower)#计算80%置信区间的上下界
fit1$upper <- exp(fit1$upper)#计算95%置信区间的上下界
p <- cbind(fit1$mean,fit1$lower,fit1$upper)
p
## fit1$mean fit1$lower.80% fit1$lower.95% fit1$upper.80%
## Jan 1961 7.449110e+191 1.742223e+182 1.389185e+177 3.184967e+201
## Feb 1961 3.430214e+188 6.765500e+176 4.305623e+170 1.739172e+200
## Mar 1961 4.827129e+215 1.118607e+200 5.915653e+191 2.083052e+231
## Apr 1961 7.368359e+209 4.593671e+192 3.583203e+183 1.181902e+227
## May 1961 1.565936e+210 1.258355e+191 9.807001e+180 1.948700e+229
## fit1$upper.95%
## Jan 1961 3.994374e+206
## Feb 1961 2.732791e+206
## Mar 1961 3.938901e+239
## Apr 1961 1.515200e+236
## May 1961 2.500414e+23914.3.1.4 ets()的自动预测
即不指定model。
当抑制项存在时,往往模型更符合实际预测。一般假定长期趋势是一直向上的,而一个抑制项存在则使得在一段时间内靠近一条水平渐近线。可以通过ets()自动选择对你原始数据拟合优度最高的模型。
语法:
fit <- ets()#注意这里不指定model
fit
autoplot(forecast(fit))完整教程请查看
R语言基础学习手册