opencv——（ 二值化函数 、自适应二值化函数、腐蚀函数、膨胀函数、仿射变换函数、透视变换函数）

小成晓程2024-12-12 8:48

注：代码用到的原图

一、二值化

1.1、二值化图

二值化图：就是将图像中的像素改成只有两种值，其操作的图像必须是灰度图。

1.2、阈值法(THRESH_BINARY)

通过设置一个阈值，将灰度图中的每一个像素值与该阈值进行比较，小于等于阈值的像素就被设置为0（黑），大于阈值的像素就被设置为maxval。

python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#灰度
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

img_binary = np.zeros_like(img_gray)
#设置一个阈值
thresh = 127
for i in range(img_gray.shape[0]):
    for j in range(img_gray.shape[1]):
        if img_gray[i,j] <= thresh:
            img_binary[i,j] = 0
        else:
            img_binary[i,j] = 255

cv2.imshow("img_binary",img_binary)
cv2.waitKey(0)

1.2.2、反阈值法(THRESH_BINARY_INV)

与阈值法相反。反阈值法是当灰度图的像素值大于阈值时，该像素值将会变成0（黑），当灰度图的像素值小于等于阈值时，该像素值将会变成maxval。

python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#灰度
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

img_binary = np.zeros_like(img_gray)
#设置一个阈值
thresh = 127
for i in range(img_gray.shape[0]):
    for j in range(img_gray.shape[1]):
        if img_gray[i,j] > thresh:
            img_binary[i,j] = 0
        else:
            img_binary[i,j] = 255

cv2.imshow("img_binary",img_binary)
cv2.waitKey(0)

1.3、截断阈值法(THRESH_TRUNC)：

指将灰度图中的所有像素与阈值进行比较，像素值大于阈值的部分将会被修改为阈值，小于等于阈值的部分不变。换句话说，经过截断阈值法处理过的二值化图中的最大像素值就是阈值。

python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#灰度
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

img_binary = np.zeros_like(img_gray)
#设置一个阈值
thresh = 127
for i in range(img_gray.shape[0]):
    for j in range(img_gray.shape[1]):
        if img_gray[i,j] <= thresh:
            img_binary[i,j] = img_gray[i,j]
        else:
            img_binary[i,j] = thresh

cv2.imshow("img_binary",img_binary)
cv2.waitKey(0)

1.4、低阈值零处理(THRESH_TOZERO)

就是像素值小于等于阈值的部分被置为0（也就是黑色），大于阈值的部分不变。

python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#灰度
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

img_binary = np.zeros_like(img_gray)
#设置一个阈值
thresh = 127
for i in range(img_gray.shape[0]):
    for j in range(img_gray.shape[1]):
        if img_gray[i,j] <= thresh:
            img_binary[i,j] = 0
        else:
            img_binary[i,j] = img_gray[i,j]

cv2.imshow("img_binary",img_binary)
cv2.waitKey(0)

1.5、超阈值零处理(THRESH_TOZERO_INV)

就是将灰度图中的每个像素与阈值进行比较，像素值大于阈值的部分置为0（也就是黑色），像素值小于等于阈值的部分不变。

python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#灰度
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

img_binary = np.zeros_like(img_gray)
#设置一个阈值
thresh = 127
for i in range(img_gray.shape[0]):
    for j in range(img_gray.shape[1]):
        if img_gray[i,j] <= thresh:
            img_binary[i,j] = img_gray[i,j]
        else:
            img_binary[i,j] = 0

cv2.imshow("img_binary",img_binary)
cv2.waitKey(0)

1.6、OTSU阈值法

在介绍OTSU阈值法之前，我们首先要了解一下双峰图片的概念。

双峰图片就是指灰度图的直方图上有两个峰值，直方图就是对灰度图中每个像素值的点的个数的统计图，如下图所示。

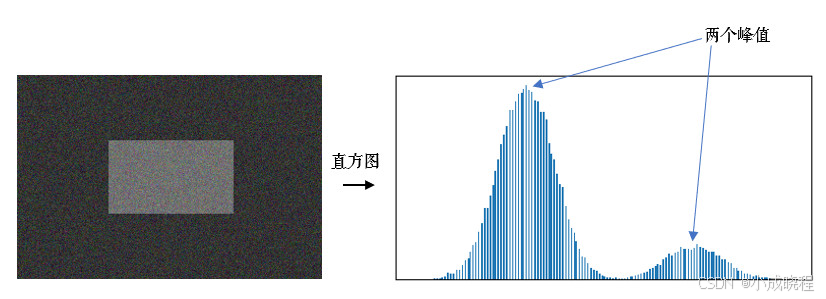
OTSU算法是通过一个值将这张图分前景色和背景色（也就是灰度图中小于这个值的是一类，大于这个值的是一类），通过统计学方法（最大类间方差）来验证该值的合理性，当根据该值进行分割时，使用最大类间方差计算得到的值最大时，该值就是二值化算法中所需要的阈值。通常该值是从灰度图中的最小值加1开始进行迭代计算，直到灰度图中的最大像素值减1，然后把得到的最大类间方差值进行比较，来得到二值化的阈值。以下是一些符号规定：

下面举个例子，有一张大小为4×4的图片，假设阈值T为1，那么：

也就是这张图片根据阈值1分为了前景（像素为2的部分）和背景（像素为0）的部分，并且计算出了OTSU算法所需要的各个数据，根据上面的数据，我们给出计算方差的公式：

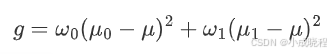
g就是前景与背景两类之间的方差，这个值越大，说明前景和背景的差别就越大，效果就越好。OTSU算法就是在灰度图的像素值范围内遍历阈值T，使得g最大，基本上双峰图片的阈值T在两峰之间的谷底。

功能： 用于对图像进行二值化处理
参数：

  • src: 输入图像，这应该是一个灰度图像（即单通道图像）。如果你有一个彩色图像，你需要先使用 cv2.cvtColor() 将其转换为灰度图。
  • thresh: 阈值，用于将像素划分为两部分。这个值是一个浮点数或整数，取决于图像的数据类型。
  • maxVal: 最大值，用于设置高于阈值的像素值。这个值通常是一个整数，表示你想要将高于阈值的像素设置为的具体数值。
  • type: 阈值类型，这是一个标志，用于指定如何应用阈值。OpenCV 提供了几种不同的阈值类型，如 cv2.THRESH_BINARY、cv2.THRESH_BINARY_INV、cv2.THRESH_TRUNC、cv2.THRESH_TOZERO 和 cv2.THRESH_TOZERO_INV。
  • dst: 输出图像，与输入图像具有相同的大小和类型。这是一个可选参数，如果不提供，函数会创建一个新的图像来存储二值化结果。
    函数返回值：
  • ret: 实际使用的阈值。在某些情况下（如使用 cv2.THRESH_OTSU 或 cv2.THRESH_TRIANGLE 标志时），这个值可能会与输入的 thresh 不同。
  • dst: 二值化后的图像。

eg:将图像进行二值化

python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#灰度
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

ret,img_binary = cv2.threshold(img_gray,127,255,cv2.THRESH_BINARY+ cv2.THRESH_OTSU)
cv2.imshow("img_binary",img_binary)
cv2.waitKey(0)

二、自适应二值化

与二值化算法相比，自适应二值化更加适合用在明暗分布不均的图片，因为图片的明暗不均，导致图片上的每一小部分都要使用不同的阈值进行二值化处理，这时候传统的二值化算法就无法满足我们的需求了，于是就出现了自适应二值化。

自适应二值化方法会对图像中的所有像素点计算其各自的阈值，这样能够更好的保留图片里的一些信息。自适应二值化组件内容如下图所示：

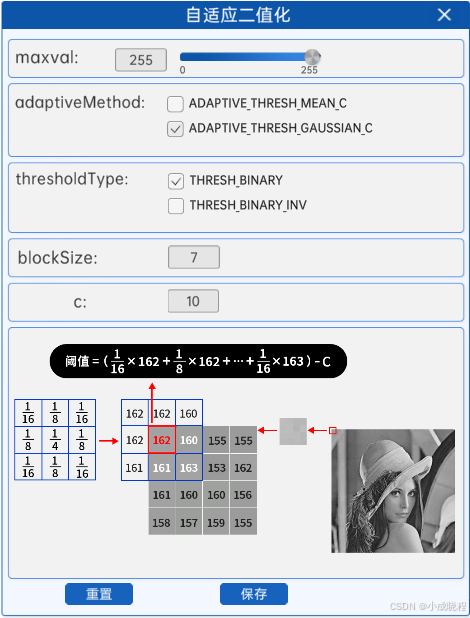
其中各个参数的含义如下：

maxval：最大阈值，一般为255

adaptiveMethod：小区域阈值的计算方式：

ADAPTIVE_THRESH_MEAN_C：小区域内取均值

ADAPTIVE_THRESH_GAUSSIAN_C：小区域内加权求和，权重是个高斯核

thresholdType：二值化方法，只能使用THRESH_BINARY、THRESH_BINARY_INV，也就是阈值法和反阈值法

blockSize：选取的小区域的面积，如7就是7*7的小块。

c：最终阈值等于小区域计算出的阈值再减去此值

下面介绍一下这两种方法。

2.1 取均值

比如一张图片的左上角像素值如下图所示：

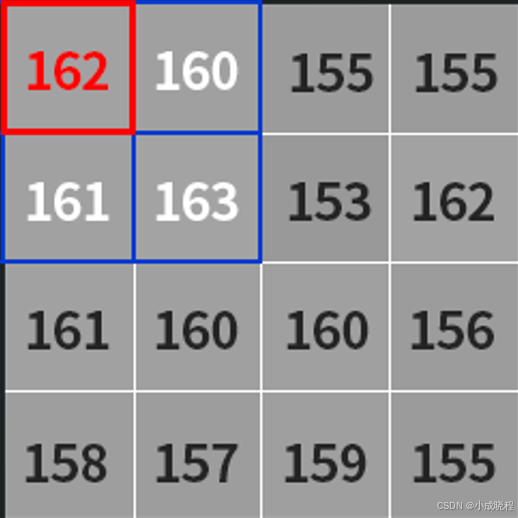
假如我们使用的小区域是3*3的，那么就会从图片的左上角开始（也就是像素值为162的地方）计算其邻域内的平均值，如果处于边缘地区就会对边界进行填充，填充值就是边界的像素点，如下图所示：

那么对于左上角像素值为162的这个点，161（也就是上图中括号内的计算结果，结果会进行取整）就是根据平均值计算出来的阈值，接着减去一个固定值C，得到的结果就是左上角这个点的二值化阈值了，接着根据选取的是阈值法还是反阈值法进行二值化操作。紧接着，向右滑动计算每个点的邻域内的平均值，直到计算出右下角的点的阈值为止。我们所用到的不断滑动的小区域被称之为核，比如3*3的小区域叫做3*3的核，并且核的大小都是奇数个，也就是3*3、5*5、7*7等。

2.2 加权求和

对小区域内的像素进行加权求和得到新的阈值，其权重值来自于高斯分布。

高斯分布，通过概率密度函数来定义高斯分布，一维高斯概率分布函数为：

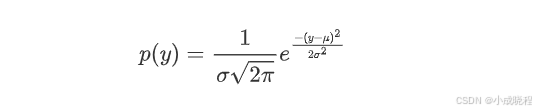
通过改变函数中和的值，我们可以得到如下图像，其中均值为，标准差为。

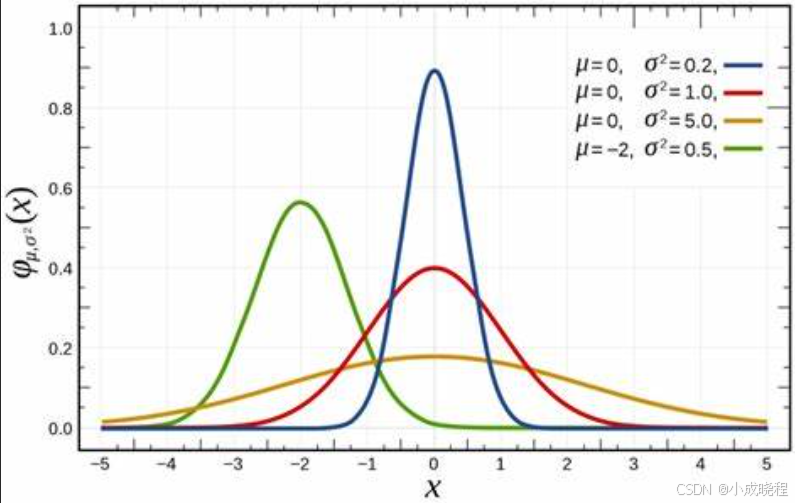
此时我们拓展到二维图像，一般情况下我们使x轴和y轴的相等并且，此时我们可以得到二维高斯函数的表达式为：

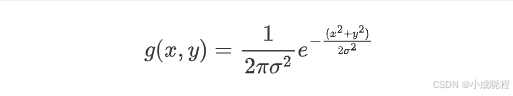
高斯概率函数是相对于二维坐标产生的，其中（x,y）为点坐标，要得到一个高斯滤波器模板，应先对高斯函数进行离散化，将得到的值作为模板的系数。例如：要产生一个3*3的高斯权重核，以核的中心位置为坐标原点进行取样，其周围的坐标如下图所示（x轴水平向右，y轴竖直向上）

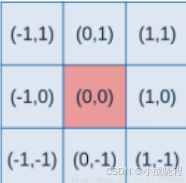
将坐标带入上面的公式中，即可得到一个高斯权重核。

而在opencv里，当kernel(小区域)的尺寸为1、3、5、7并且用户没有设置sigma的时候(sigma

|----------|---------------------------------------------------------------------|
| kernel尺寸 | 核值 |
| 1 | [1] |
| 3 | [0.25, 0.5, 0.25] |
| 5 | [0.0625, 0.25, 0.375, 0.25, 0.0625] |
| 7 | [0.03125, 0.109375, 0.21875, 0.28125, 0.21875, 0.109375, 0.03125] |

比如kernel的尺寸为3*3时，使用

进行矩阵的乘法，就会得到如下的权重值，其他的类似。

通过这个高斯核，即可对图片中的每个像素去计算其阈值，并将该阈值减去固定值得到最终阈值，然后根据二值化规则进行二值化。

而当kernels尺寸超过7的时候,如果sigma设置合法(用户设置了sigma),则按照高斯公式计算.当sigma不合法(用户没有设置sigma),则按照如下公式计算sigma的值：

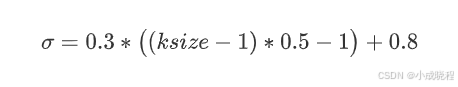
某像素点的阈值计算过程如下图所示：

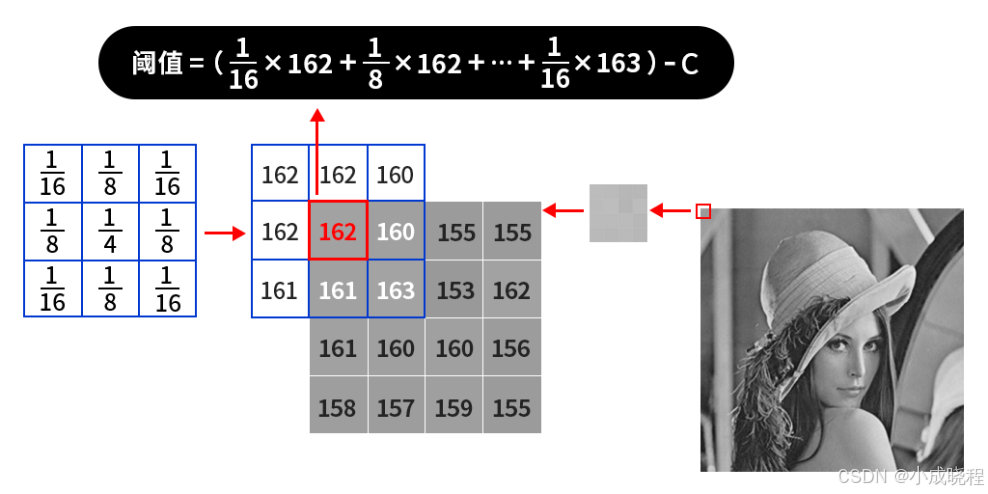
首先还是对边界进行填充，然后计算原图中的左上角（也就是162像素值的位置）的二值化阈值，其计算过程如上图所示，再然后根据选择的二值化方法对左上角的像素点进行二值化，之后核向右继续计算第二个像素点的阈值，第三个像素点的阈值...直到右下角（也就是155像素值的位置）为止。

当核的大小不同时，仅仅是核的参数会发生变化，计算过程与此是一样的。


功能： 对图像应用自适应阈值处理。
参数：

  • src: 输入图像，必须为灰度图像。
  • maxValue: 超过或等于阈值的像素值被赋予的值。它可以是任意数值，但通常设置为 255（表示白色）。
  • adaptiveMethod: 自适应阈值算法的选择。有两种选择：
    • cv2.ADAPTIVE_THRESH_MEAN_C：计算邻域的平均值，然后从平均值中减去常数 C。
    • cv2.ADAPTIVE_THRESH_GAUSSIAN_C：计算邻域像素的加权和（使用高斯窗口），然后从加权和中减去常数 C。
  • thresholdType: 阈值类型，与固定阈值函数 cv2.threshold() 相同。通常是 cv2.THRESH_BINARY 或 cv2.THRESH_BINARY_INV。
  • blockSize: 用于计算阈值的邻域大小（必须是奇数）。
  • C: 从计算出的平均值或加权和中减去的常数。
python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#灰度
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

img_adaptive_binary = cv2.adaptiveThreshold(img_gray,# 参数1 灰度图
                                            255,# 参数2 最大值
                                            cv2.ADAPTIVE_THRESH_GAUSSIAN_C, # 参数3 自适应方法
                                            cv2.THRESH_BINARY,  # 参数4 二值化类型
                                            7,  # 参数5 核的大小
                                            5  # 参数6 计算的阈值减去这个常数是最终阈值
                                            )
cv2.imshow("img_adaptive_binary",img_adaptive_binary)
cv2.waitKey(0)

三、腐蚀

腐蚀操作就是使用核在原图（二值化图）上进行从左到右、从上到下的滑动（也就是从图像的左上角开始，滑动到图像的右下角）。在滑动过程中，令核值为1的区域与被核覆盖的对应区域进行相乘，得到其最小值，该最小值就是卷积核覆盖区域的中心像素点的新像素值，接着继续滑动。由于操作图像为二值图，所以不是黑就是白，这就意味着，在被核值为1覆盖的区域内，只要有黑色（像素值为0），那么该区域的中心像素点必定为黑色（0）。这样做的结果就是会将二值化图像中的白色部分尽可能的压缩，如下图所示，该图经过腐蚀之后，"变瘦"了。


功能： 用于对图像进行腐蚀操作
参数：

  • src: 输入图像，这可以是一个二值图像、灰度图像或彩色图像。对于二值图像，通常使用 0 和 255 表示像素值；对于灰度图像和彩色图像，像素值范围可能更广。
  • kernel: 结构元素，核。
  • dst: 输出图像，是一个可选参数，如果不提供，函数会创建一个新的图像来存储腐蚀结果。
  • anchor: 锚点，这是一个可选参数，通常不需要修改。
  • iterations: 迭代次数，表示腐蚀操作应该应用的次数。默认值为 1，但你可以通过增加这个值来应用多次腐蚀，从而得到更强的效果。
  • borderType: 边界类型，用于指定图像边界的像素外推方法。这通常是一个可选参数，默认值为 cv2.BORDER_DEFAULT，表示使用默认的边界填充方法。
  • borderValue: 边界值，当 borderType 为 cv2.BORDER_CONSTANT 时使用，表示边界像素应该被设置的值。这也是一个可选参数。
    函数返回值：
  • dst: 腐蚀后的图像，这是一个包含腐蚀操作结果的 NumPy 数组。
python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#灰度
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

img_adaptive_binary = cv2.adaptiveThreshold(img_gray,# 参数1 灰度图
                                            255,# 参数2 最大值
                                            cv2.ADAPTIVE_THRESH_GAUSSIAN_C, # 参数3 自适应方法
                                            cv2.THRESH_BINARY,  # 参数4 二值化类型
                                            7,  # 参数5 核的大小
                                            5  # 参数6 计算的阈值减去这个常数是最终阈值
                                            )
# 进行腐蚀操作
# 1、创建结构化元素 / 核
kernal = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(3,3))
# 2、调用腐蚀函数
img_erode = cv2.erode(img_adaptive_binary,kernal)

cv2.imshow("img_adaptive_binary",img_adaptive_binary)
cv2.imshow('img_erode',img_erode)
cv2.waitKey(0)

四、 膨胀

膨胀与腐蚀刚好相反，膨胀操作就是使用核在原图（二值化图）上进行从左到右、从上到下的滑动（也就是从图像的左上角开始，滑动到图像的右下角），在滑动过程中，令核值为1的区域与被核覆盖的对应区域进行相乘，得到其 最大值，该最大值就是核覆盖区域的中心像素点的新像素值，接着继续滑动。由于操作图像为二值图，所以不是黑就是白，这就意味着，在卷积核覆盖的区域内，只要有白色（像素值为255），那么该区域的中心像素点必定为白色（255）。这样做的结果就是会将二值化图像中的白色部分尽可能的扩张，如下图所示，该图经过腐蚀之后，"变胖"了。

功能：对图像进行膨胀操作
参数：

  • src: 输入图像，这可以是一个二值图像、灰度图像或彩色图像。
  • kernel: 结构元素，。
  • dst: 输出图像，是一个可选参数，如果不提供，函数会创建一个新的图像来存储膨胀结果。
  • anchor: 锚点。
  • iterations: 迭代次数，表示膨胀操作应该应用的次数。默认值为 1，但可以通过增加这个值来应用多次膨胀，从而得到更强的效果。
  • borderType: 边界类型，用于指定图像边界的像素外推方法。默认值为 cv2.BORDER_DEFAULT。
  • borderValue: 边界值，当 borderType 为 cv2.BORDER_CONSTANT 时使用，表示边界像素应该被设置的值。
    函数返回值：
  • dst: 膨胀后的图像，这是一个包含膨胀操作结果的 NumPy 数组。
python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#灰度
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

img_adaptive_binary = cv2.adaptiveThreshold(img_gray,# 参数1 灰度图
                                            255,# 参数2 最大值
                                            cv2.ADAPTIVE_THRESH_GAUSSIAN_C, # 参数3 自适应方法
                                            cv2.THRESH_BINARY,  # 参数4 二值化类型
                                            7,  # 参数5 核的大小
                                            5  # 参数6 计算的阈值减去这个常数是最终阈值
                                            )
# 进行腐蚀操作
# 1、创建结构化元素 / 核
kernal = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(3,3))
# 2、调用腐蚀函数
img_erode = cv2.dilate(img_adaptive_binary,kernal)

cv2.imshow("img_adaptive_binary",img_adaptive_binary)
cv2.imshow('img_erode',img_erode)
cv2.waitKey(0)

五、 仿射变换函数

1、ROI切割

ROI：Region of Interest，翻译过来就是感兴趣的区域。什么意思呢？比如对于一个人的照片，假如我们要检测眼睛，因为眼睛肯定在脸上，所以我们感兴趣的只有脸这部分，其他都不care，所以可以单独把脸截取出来，这样就可以大大节省计算量，提高运行速度。

我们在使用OpenCV进行读取图像时，图像数据会被存储为Numpy数组，这也意味着我们可以使用Numpy数组的一些操作来对图像数据进行处理，比如切片。而本实验的原理也是基于Numpy数组的切片操作来完成的，因此在对应的组件中就需要填我们要切割的ROI区域的坐标来完成ROI切割操作。

注意：在OpenCV中，坐标的x轴的正方向是水平向右，y轴的正方向是垂直向下，与数学上的二维坐标并不相同。

在计算机视觉中，当我们使用OpenCV读取RGB三通道图像时，它会被转换成一个三维的Numpy数组。这个数组里的每个元素值都表示图像的一个像素值。这个三维数组的第一个维度（即轴0）通常代表图像的高度，第二个维度（即轴1）代表图像的宽度，而第三个维度（即轴2）代表图像的三个颜色通道（B、G、R，OpenCV读取到的图像以BGR的方式存储）所对应的像素值。

因此，我们可以通过指定切片的范围来选择特定的高度和宽度区域。这样，我们就能够获取这个区域内的所有像素值，即得到了这个区域的图像块，通过Numpy的切片操作，我们就完成了ROI切割的操作。这种提取ROI的方法允许我们仅获取感兴趣区域内的像素，而忽略其他不相关的部分，从而大大减少数据处理和存储的负担。

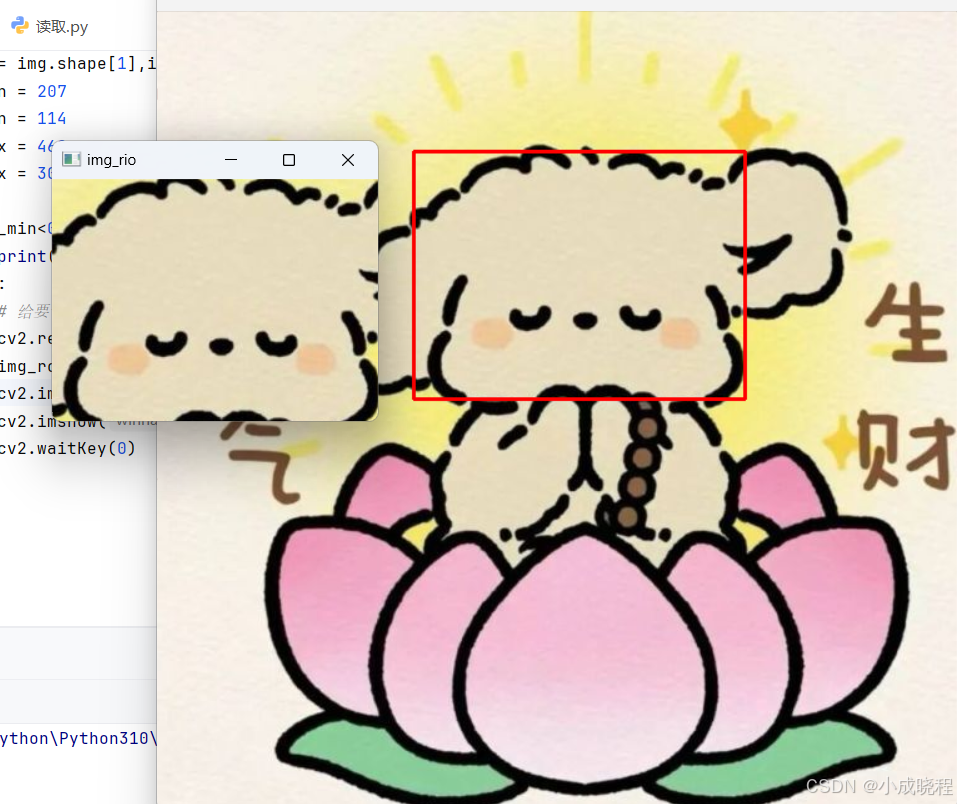
python 复制代码 
import cv2
import numpy as np

#读取图片
img = cv2.imread('./011.jpg')
#提取图片的高度宽度
w,h = img.shape[1],img.shape[0]
x_min = 207
y_min = 114
x_max = 468
y_max = 308

if x_min<0 or x_min>w or y_min<0 or y_max>h:
    print("None")
else:
    # 给要切割的内容画个框
    cv2.rectangle(img,(x_min-2,y_min-2),(x_max+2,y_max+2),(0,0,255),2)
    img_roi = img[y_min:y_max, x_min:x_max]
    cv2.imshow("img", img)
    cv2.imshow("img_rio",img_roi)
    cv2.waitKey(0)

2、图像旋转

图像旋转是指图像以某一点为旋转中心，将图像中的所有像素点都围绕该点旋转一定的角度，并且旋转后的像素点组成的图像与原图像相同。

3.2.1. 单点旋转

首先我们以最简单的一个点的旋转为例子，且以最简单的情况举例，令旋转中心为坐标系中心O（0，0），假设有一点P0 (x 0,y 0)，P 0离旋转中心O的距离为r，OP 0与坐标轴x轴的夹角为α，P0绕O顺时针旋转θ角后对应的点为P(x,y)，如下图所示：

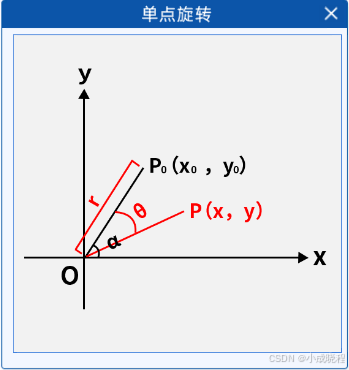
那么我们可以得到如下关系：

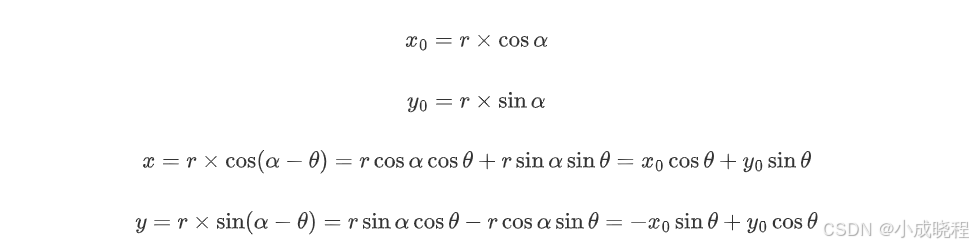
用矩阵来表示就是

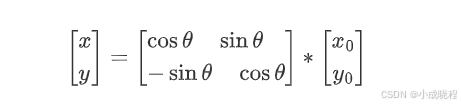
然而，在OpenCV中，旋转时是以图像的左上角为旋转中心，且以逆时针为正方向，因此上面的例子中其实是个负值，那么该矩阵可写为：

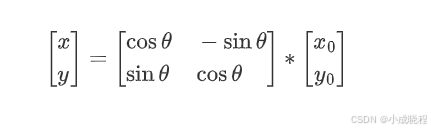
其中，

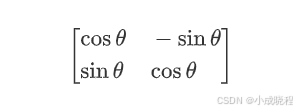
也被称作旋转矩阵。然而我们所要的不仅仅是可以围绕图像左上角进行旋转，而是可以围绕任意点进行旋转。那么我们可以将其转化成绕原点的旋转，其过程为：

  1. 首先将旋转点移到原点
  2. 按照上面的旋转矩阵进行旋转得到新的坐标点
  3. 再将得到的旋转点移回原来的位置
    也就是说，在以任意点为旋转中心时，除了要进行旋转之外，还要进行平移操作。那么当点经过平移后得到P点时，如下图所示：


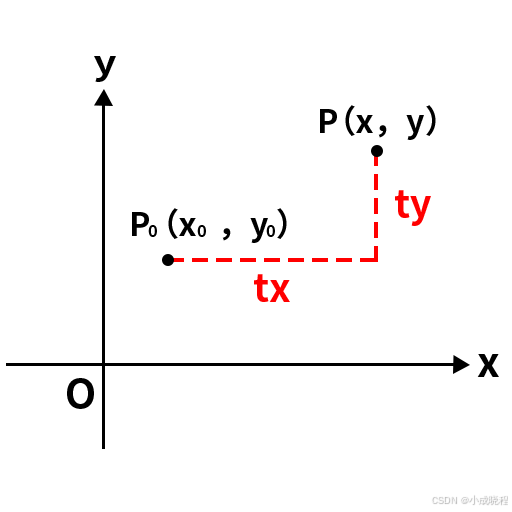
    从平移和旋转的矩阵可以看出，3x3矩阵的前2x2部分是和旋转相关的，第三列与平移相关。有了上面的表达式之后，我们就可以得到二维空间中绕任意点旋转的旋转矩阵了，只需要将旋转矩阵先左乘

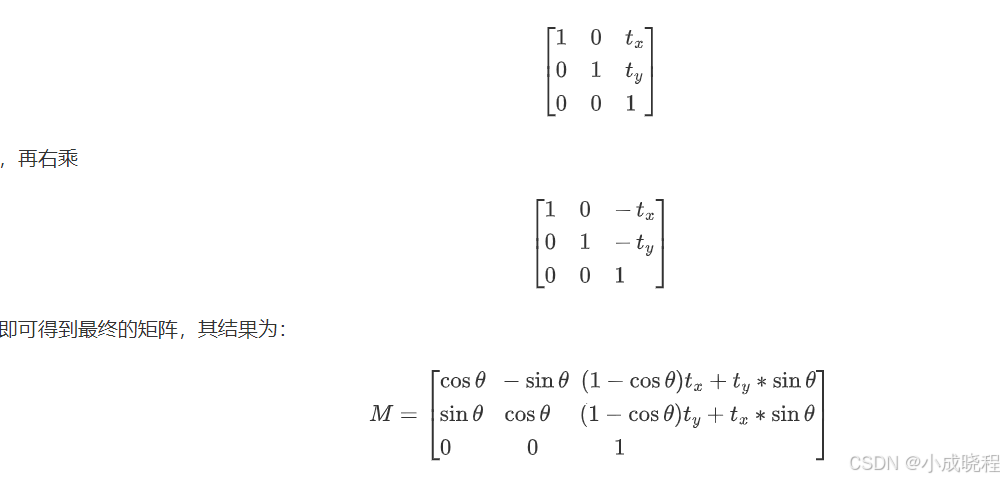
    于是我们就可以根据这个矩阵计算出图像中任意一点绕某点旋转后的坐标了，这个矩阵学名叫做仿射变换矩阵，而仿射变换是一种二维坐标到二维坐标之间的线性变换，也就是只涉及一个平面内二维图形的线性变换，图像旋转就是仿射变换的一种。它保持了二维图形的两种性质：
  4. 平直性：直线经过变换后依然是直线。
  5. 平行性：平行线经过变换后依然是平行线。

2. 图片旋转

明白了单个点的旋转过程之后，其实图像旋转也很好理解，就是将图像里的每个像素点都带入仿射变换矩阵里，从而得到旋转后的新坐标。在OpenCV中，要得到仿射变换矩阵可以使用cv2.getRotationMatrix2D()，通过这个函数即可直接获取到上面的旋转矩阵，该函数需要接收的参数为：

  • Center：表示旋转的中心点，是一个二维的坐标点(x,y)
  • Angle：表示旋转的角度
  • Scale：表示缩放比例，可以通过该参数调整图像相对于原始图像的大小变化
    因此，在本实验中只需要在组件中填好图片要旋转的角度与缩放的比例即可。

    但是这里会有一个问题，由于三角函数的值是小数，那么其乘积也会是小数，虽然OpenCV中会对其进行取整操作，但是像素点旋转之后的取整结果也有可能重合，这样就会导致可能会在旋转的过程中丢失一部分原始的像素信息。并且如果使用了scale参数进行图像的缩放的话，当图像放大时，比如一个10*10的图像放大成20*20，图像由100个像素点变成400个像素点，那么多余的300个像素点是怎么来的？而当图像缩小时，比如一个20*20的图像缩小为10*10的图像，需要丢掉300个像素点，那到底要怎么丢才能保证图像还能是一个正常的图像？ 因此我们需要一种方法来帮我们计算旋转后的图像中每一个像素点所对应的像素值，从而保证图像的完整性，这种方法就叫做插值法。

3. 插值方法

在图像处理和计算机图形学中，插值（Interpolation）是一种通过已知数据点之间的推断或估计来获取新数据点的方法。它在图像处理中常用于处理图像的放大、缩小、旋转、变形等操作，以及处理图像中的像素值。
图像插值算法是为了解决图像缩放或者旋转等操作时，由于像素之间的间隔不一致而导致的信息丢失和图像质量下降的问题。当我们对图像进行缩放或旋转等操作时，需要在新的像素位置上计算出对应的像素值，而插值算法的作用就是根据已知的像素值来推测未知位置的像素值。本实验提供了五种常见的插值算法，下面一一介绍。

3.1 最近邻插值

首先给出目标点与原图像点之间坐标的计算公式：

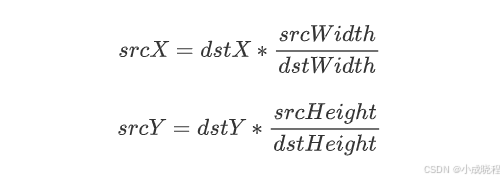
其中，dstX表示目标图像中某点的x坐标，srcWidth表示原图的宽度，dstWidth表示目标图像的宽度；dstY表示目标图像中某点的y坐标，srcHeight表示原图的高度，dstHeight表示目标图像的高度。而srcX和srcY则表示目标图像中的某点对应的原图中的点的x和y的坐标。通俗的讲，该公式就是让目标图像中的每个像素值都能找到对应的原图中的像素值，这样才能根据不同的插值方法来获取新的像素值。
根据该公式，我们就可以得到每一个目标点所对应的原图像的点，比如一个2*2的图像放大到4*4，如下图所示，其中红色的为每个像素点的坐标，绿色的则表示该像素点的像素值。

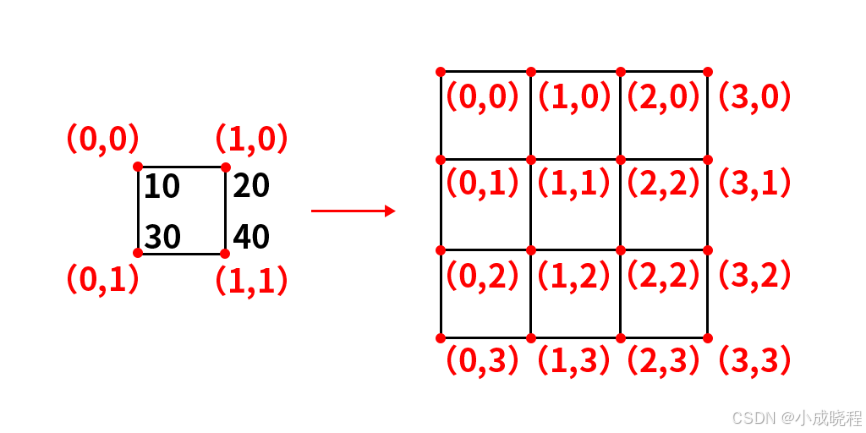
那么根据公式我们就可以计算出放大后的图像（0，0）点对应的原图像中的坐标为：

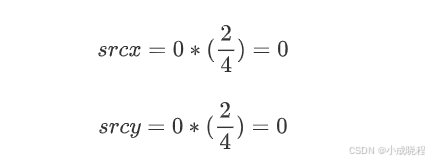
也就是原图中的（0，0）点，而最近邻插值的原则是：目标像素点的像素值与经过该公式计算出来的对应的像素点的像素值相同，如出现小数部分需要进行取整。那么放大后图像的（0，0）坐标处的像素值就是原图像中（0，0）坐标处的像素值，也就是10。
接下来就是计算放大后图像（1，0）点对应的原图像的坐标，还是带入公式：

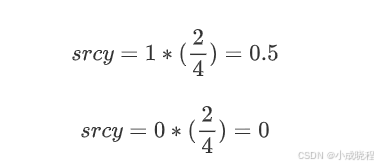
也就是原图中的（0.5，0）点，因此需要对计算出来的坐标值进行取整，取整后的结果为（0，0），也就是说放大后的图像中的（1，0）坐标处对应的像素值就是原图中（0，0）坐标处的像素值，其他像素点计算规则与此相同。

3.2 双线性插值

双线性插值算法是一种比较好的图像缩放算法，它充分的利用了原图中虚拟点四周的四个真实存在像素点的值来共同决定目标图中的一个像素点的值，因此缩放效果比简单的最邻近插值要好很多，缩放后图像质量高，不会出现值不连续的情况。
那我们先说一下线性插值是什么，假如已知两个点(x **{0},y** {0})和(x **{1},y** {1})，我们要计算[x **{0},y**{0}]区间内某一位置x在直线上的y值，那么计算过程为：

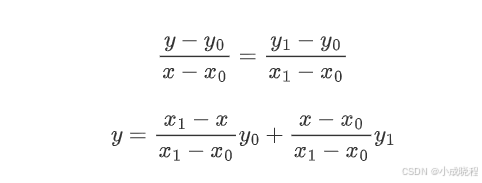
仔细看公式，其实就是计算距离，并将距离作为一个权重用于y **{0}和y**{1}的加权求和。这就是线性插值，而双线性插值本质上就是在两个方向上做线性插值。
还是给出目标点与原图像中点的计算公式：

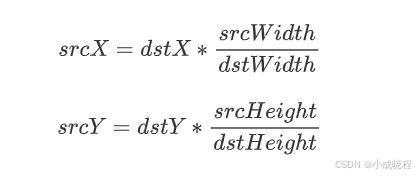
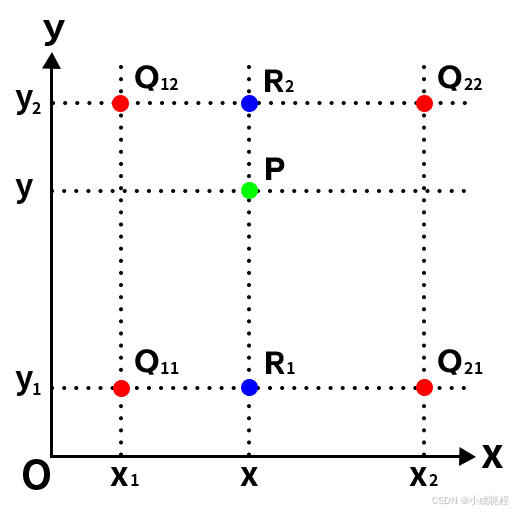
比如我们根据上述公式计算出了新图像中的某点所对应的原图像的点P，其周围的点分别为Q12、Q22、Q11、Q21， 要插值的P点不在其周围点的连线上，这时候就需要用到双线性插值了。首先延申P点得到P和Q11、Q21的交点R1与P和Q12、Q22的交点R2，如下图所示：

然后根据Q11、Q21得到R1的插值，根据Q12、Q22得到R2的插值，然后根据R1、R2得到P的插值即可，这就是双线性插值。以下是计算过程：

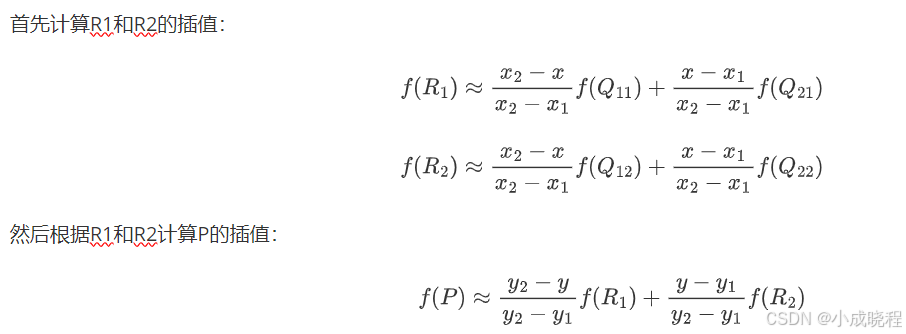
这样就得到了P点的插值。注意此处如果先在y方向插值、再在x方向插值，其结果与按照上述顺序双线性插值的结果是一样的。
双线性插值的对应关系看似比较清晰，但还是有2个问题。首先是根据坐标系的不同，产生的结果不同，这张图是左上角为坐标系原点的情况，我们可以发现最左边x=0的点都会有概率直接复制到目标图像中（至少原点肯定是这样），而且就算不和原图像中的点重合，也相当于进行了1次单线性插值（带入到权重公式中会发现结果）。

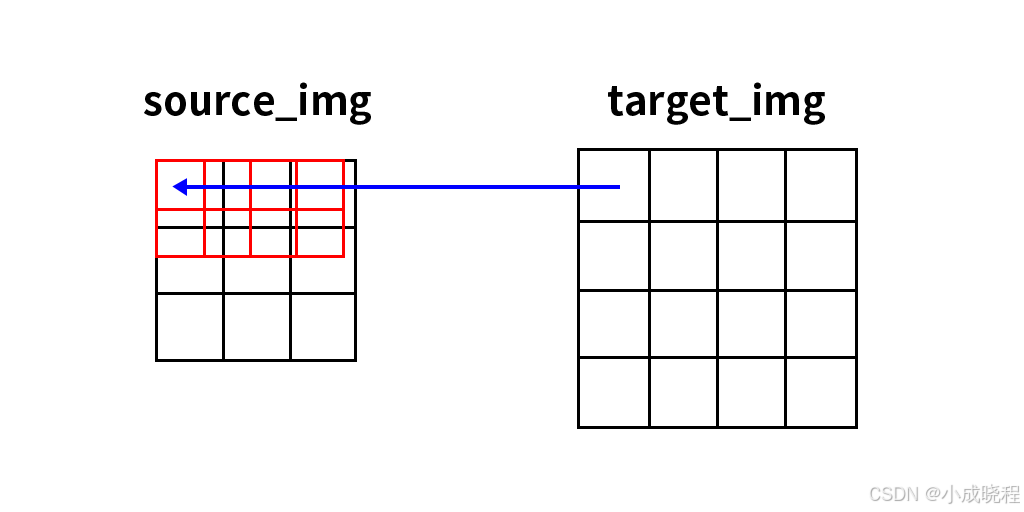
下面这张图是右上角为坐标系原点的情况，我们可以发现最右面的点都会有概率直接复制到目标图像中（至少原点肯定是这样），而且就算不和原图像中的点重合，也相当于进行了1次单线性插值。那么当我们采用不同的坐标系时产生的结果是不一样的，而且无论我们采用什么坐标系，最左侧和最右侧（最上侧和最下侧）的点是"不公平的"，这是第一个问题。

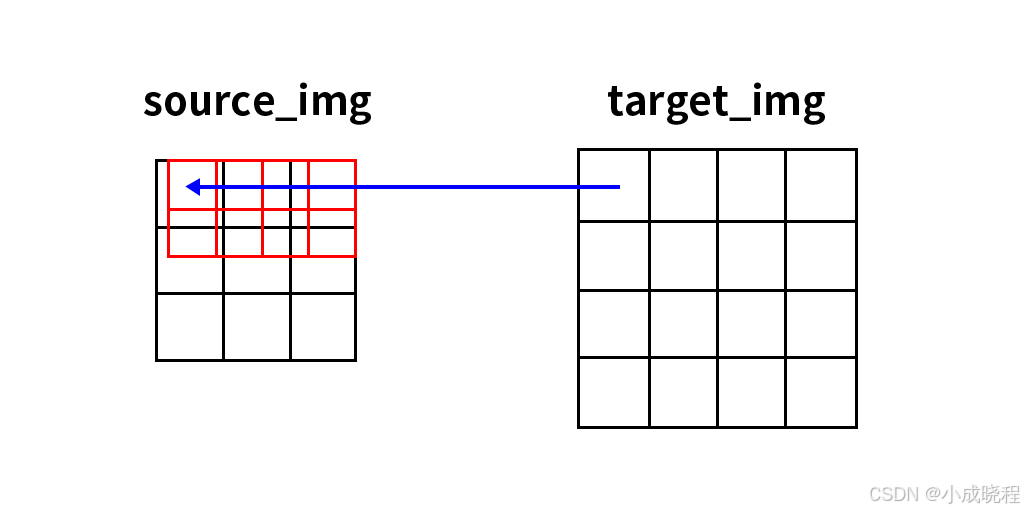
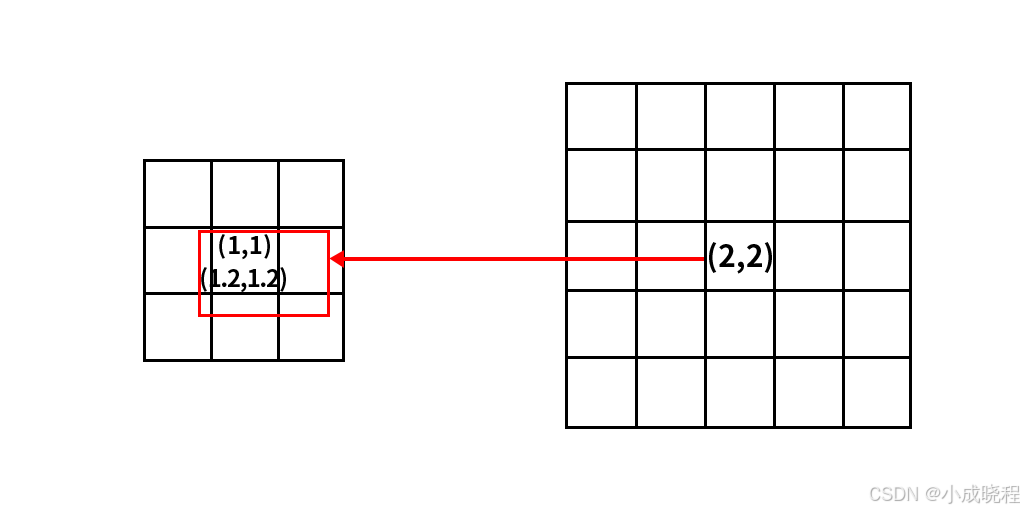
第二个问题时整体的图像相对位置会发生变化。如下图所示，左侧是原图像(3，3)，右侧是目标图像(5，5)，原图像的几何中心点是(1,1)，目标图像的几何中心点是(2,2)，根据对应关系，目标图像的几何中心点对应的原图像的位置是(1.2,1.2)，那么问题来了，目标图像的原点(0,0)和原始图像的原点是重合的，但是目标图像的几何中心点相对于原始图像的几何中心点偏右下，那么整体图像的位置会发生偏移，所以参与计算的点相对都往右下偏移会产生相对的位置信息损失。这是第二个问题。

因此，在OpenCV中，为了解决这两个问题，将公式进行了优化，如下所示：

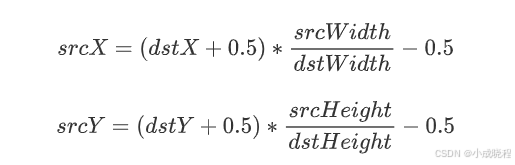
使用该公式计算出原图中的对应坐标后再进行插值计算，就不会出现上面的情况了。

3.3 像素区域插值

像素区域插值主要分两种情况，缩小图像和放大图像的工作原理并不相同。
当使用像素区域插值方法进行缩小图像时，它就会变成一个均值滤波器（滤波器其实就是一个核，这里只做简单了解，后面实验中会介绍），其工作原理可以理解为对一个区域内的像素值取平均值。
当使用像素区域插值方法进行放大图像时，如果图像放大的比例是整数倍，那么其工作原理与最近邻插值类似；如果放大的比例不是整数倍，那么就会调用双线性插值进行放大。
其中目标像素点与原图像的像素点的对应公式如下所示：

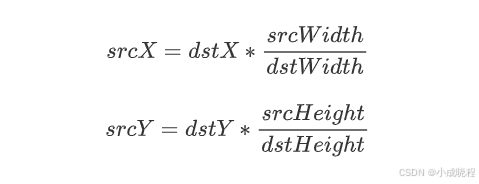
3.4 双三次插值

与双线性插值法相同，该方法也是通过映射，在映射点的邻域内通过加权来得到放大图像中的像素值。不同的是，双三次插值法需要原图像中近邻的16个点来加权。
目标像素点与原图像的像素点的对应公式如下所示：

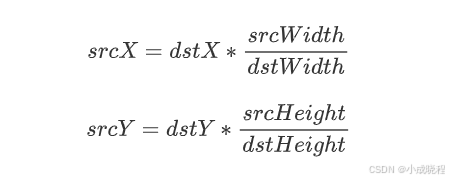
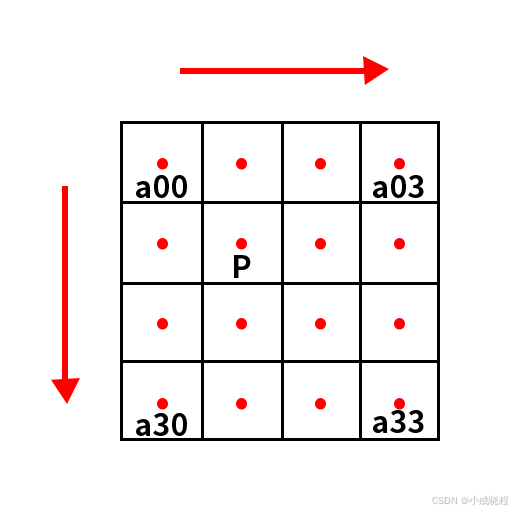
下面我们举例说明，假设原图像A大小为m*n，缩放后的目标图像B的大小为M*N。其中A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一个像素点（X,Y）的值，必须先找出像素（X,Y）在原图像A中对应的像素（x,y），再根据原图像A距离像素（x,y）最近的16个像素点作为计算目标图像B（X,Y）处像素值的参数，利用BiCubic基函数求出16个像素点的权重，图B像素（x,y）的值就等于16个像素点的加权叠加。
假如下图中的P点就是目标图像B在（X,Y）处根据上述公式计算出的对应于原图像A中的位置，P的坐标位置会出现小数部分，所以我们假设P点的坐标为（x+u,y+v），其中x、y表示整数部分，u、v表示小数部分，那么我们就可以得到其周围的最近的16个像素的位置，我们用a（i，j）（i，j=0,1,2,3）来表示，如下图所示。

然后给出BiCubic函数：

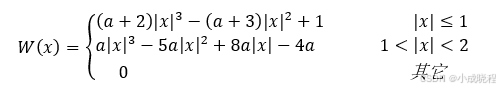
其中，a一般取-0.5或-0.75。
我们要做的就是将上面的16个点的坐标带入函数中，获取16像素所对应的权重W(x)。然而BiCubic函数是一维的，所以我们需要将像素点的行与列分开计算，比如a00这个点，我们需要将x=0带入BiCubic函数中，计算a00点对于P点的x方向的权重，然后将y=0带入BiCubic函数中，计算a00点对于P点的y方向的权重，其他像素点也是这样的计算过程，最终我们就可以得到P所对应的目标图像B在（X,Y）处的像素值为：

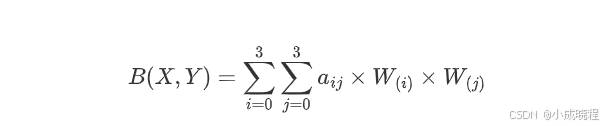
依此办法我们就可以得到目标图像中所有的像素点的像素值。

3.5 Lanczos插值

Lanczos插值方法与双三次插值的思想是一样的，不同的就是其需要的原图像周围的像素点的范围变成了8*8，并且不再使用BiCubic函数来计算权重，而是换了一个公式计算权重。
首先还是目标像素点与原图像的像素点的对应公式如下所示：

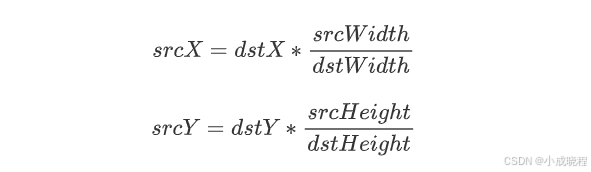
下面我们举例说明，假设原图像A大小为m*n，缩放后的目标图像B的大小为M*N。其中A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一个像素点（X,Y）的值，必须先找出像素（X,Y）在原图像A中对应的像素（x,y），再根据原图像A距离像素（x,y）最近的64个像素点作为计算目标图像B（X,Y）处像素值的参数，利用权重函数求出64个像素点的权重，图B像素（x,y）的值就等于64个像素点的加权叠加。
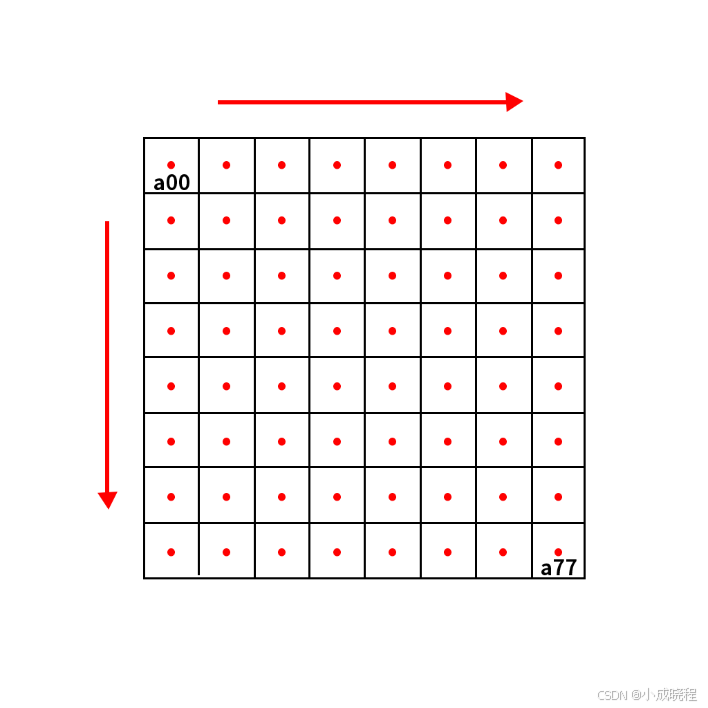
假如下图中的P点就是目标图像B在（X,Y）处根据上述公式计算出的对应于原图像A中的位置，P的坐标位置会出现小数部分，所以我们假设P点的坐标为（x+u,y+v），其中x、y表示整数部分，u、v表示小数部分，那么我们就可以得到其周围的最近的64个像素的位置，我们用a（i，j）（i，j=0,1,2,3,4,5,6,7）来表示，如下图所示。

然后给出权重公式：其中a通常取2或者3，当a=2时，该算法适用于图像缩小。a=3时，该算法适用于图像放大。

与双三次插值一样，这里也需要将像素点分行和列分别带入计算权重值，其他像素点也是这样的计算过程，最终我们就可以得到P所对应的目标图像B在（X,Y）处的像素值为：

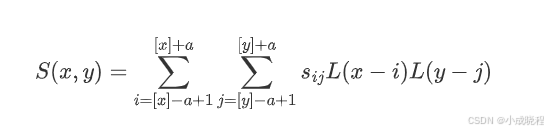
其中\[x\]、\[y\]表示对坐标值向下取整，通过该方法就可以计算出新的图像中所有的像素点的像素值。

3.6 小结

最近邻插值的计算速度最快，但是可能会导致图像出现锯齿状边缘和失真，效果较差。双线性插值的计算速度慢一点，但效果有了大幅度的提高，适用于大多数场景。双三次插值、Lanczos插值的计算速度都很慢，但是效果都很好。
在OpenCV中，关于插值方法默认选择的都是双线性插值，且一般情况下双线性插值已经能满足大
部分需求。

4. 边缘填充方式

为什么要填充边缘呢？我们已下图为例。

|---|---|
| | |

可以看到，左图在逆时针旋转45度之后原图的四个顶点在右图中已经看不到了，同时，右图的四个顶点区域其实是什么都没有的，因此我们需要对空出来的区域进行一个填充。右图就是对空出来的区域进行了像素值为（0，0，0）的填充，也就是黑色像素值的填充。除此之外，后续的一些图像处理方式也会用到边缘填充，这里介绍五个常用的边缘填充方法。

4.1 边界复制（BORDER_REPLICATE）

边界复制会将边界处的像素值进行复制，然后作为边界填充的像素值，如下图所示，可以看到四周的像素值都一样

|---|---|
| | |

4.2 边界反射（BORDER_REFLECT）

如下图所示，会根据原图的边缘进行反射。

|---|---|
| | |

4.3 边界反射101（BORDER_REFLECT_101）

与边界反射不同的是，不再反射边缘的像素点，如下图所示

|---|---|
| | |

4.4 边界常数（BORDER_CONSTANT）

当选择边界常数时，还要指定常数值是多少，默认的填充常数值为0，如下图所示

|------------------------------------------------------------------------------------------------------------------------------------------------------|---|
| | |

4.5 边界包裹（BORDER_WRAP）

如下图所示

|---|---|
| | |

cv2.getRotationMatrix2D(center, angle, scale)

功能：用于计算二维旋转矩阵的函数

参数：

center: 旋转的中心点，通常是一个二元元组 (x, y)，表示旋转中心的坐标。

angle: 旋转的角度，以度为单位。正值表示逆时针旋转，负值表示顺时针旋转。

scale: 缩放因子。默认情况下，这个值是 1.0，表示不缩放。如果你想要同时旋转和缩放图像，可以通过调整这个参数来实现。
cv2.warpAffine(src, M, dsize, dst=None, flags=None, borderMode=None, borderValue=None)

功能：用于对图像进行仿射变换（Affine Transformation）的函数，仿射变换包括平移、旋转、缩放以及剪切等操作。

参数：

src: 输入图像。

M: 变换矩阵，一个 2x3 的数组。这个矩阵是通过其他函数（如 cv2.getRotationMatrix2D()）计算得到的，用于描述仿射变换。

dsize: 输出图像的大小，以 (width, height) 的形式表示。这个参数决定了变换后图像的尺寸。

dst: 输出图像，与输入图像有相同的大小和类型。这是一个可选参数，如果提供，则变换的结果会存储在这个图像中；如果未提供，则会创建一个新的图像来存储结果。

flags: 插值方法。常用的插值方法包括 cv2.INTER_LINEAR（线性插值）、cv2.INTER_NEAREST（最近邻插值）、cv2.INTER_CUBIC（三次样条插值）等。这是一个可选参数，如果未提供，则默认使用线性插值。

borderMode: 边缘填充方法。常用的方法包括 cv2.BORDER_CONSTANT（常量填充）、cv2.BORDER_REFLECT（反射）、cv2.BORDER_REFLECT_101（反射101）等。这是一个可选参数，如果未提供，则默认使用常量填充。

borderValue: 边界颜色，当 borderMode 为 cv2.BORDER_CONSTANT 时使用。这个参数是一个表示颜色的元组或数组，如 (255, 255, 255) 表示白色。这是一个可选参数，如果未提供，则默认使用黑色 (0, 0, 0)。

python 复制代码 
import cv2

# 读取一张图片
img = cv2.imread("'./011.jpg'")

# 使用cv2.getRotationMatrix2D(center, angle, scale)获取变换矩阵
# 参数1：center 旋转的中心点(x, y), 一般选择图片的中心 （宽度的一半，高度的一半）
# 参数2：angle  旋转的角度
# 参数3：scale  缩放比例
M = cv2.getRotationMatrix2D((img.shape[1]/2, img.shape[0]/2), 45, 0.5)

# 使用cv2.warpAffine(src, M, dsize, dst=None, flags=None, borderMode=None, borderValue=None)
# 对图像进行放射变换
img_warp = cv2.warpAffine(img,  # 要旋转的图像
                          M,    # 旋转矩阵
                          (700, 700),     # 输出图像的大小 自己指定即可 可和原图不一样大小
                          flags=cv2.INTER_LINEAR,   # 插值方式
                          borderMode=cv2.BORDER_WRAP    # 边缘填充方式，默认是常数填充显示为黑色
                          )

cv2.imshow('image', img)
cv2.imshow('image_warp', img_warp)

3、图片镜像旋转

图像的旋转是围绕一个特定点进行的，而图像的镜像旋转则是围绕坐标轴进行的。图像的镜像旋转分为水平翻转、垂直翻转、水平垂直翻转三种。
水平翻转就是将图片的像素点沿y轴翻转，具体到像素点来说就是令其坐标从（x,y）翻转为（-x,y）。
垂直翻转就是将图片的像素点沿x轴翻转，具体到像素点来说就是其坐标从（x,y）翻转为（x,-y）
水平垂直翻转就是水平翻转和垂直翻转的结合，具体到像素点来说就是其坐标从（x,y）翻转为（-x,-y）。用公式表示为：

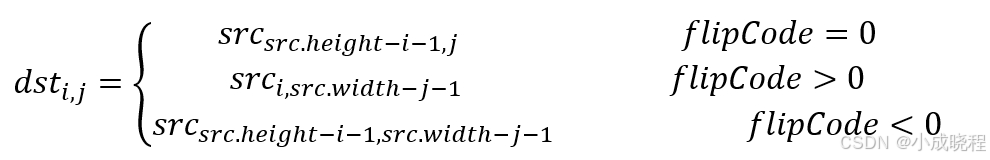
由图像的旋转我们知道，图像在旋转的时候需要有旋转中心，而图像的镜像旋转虽然都是围绕x轴和y轴进行旋转，但是我们也需要确定x轴和y轴的坐标。在OpenCV中，图片的镜像旋转是以图像的中心为原点进行镜像翻转的。也就是说，水平翻转时，图像的左侧和右侧会关于中心点进行交换，垂直翻转时，图像的上侧和下侧会关于中心点进行交换。
在本实验中，图片镜像旋转组件里的参数flipcode有三个选择：

  • 0：垂直翻转 x轴
  • 大于0：水平翻转 y轴
  • 小于0：水平垂直翻转 x轴和y轴

cv2.flip(src, flipCode, dst=None)

功能：用于翻转图像的函数

参数：

src: 输入图像，即你想要翻转的图像。

flipCode: 翻转的标志，决定了翻转的方式。它可以是以下三个值之一：

0：表示沿 x 轴翻转（垂直翻转）。

1：表示沿 y 轴翻转（水平翻转）。这是最常用的翻转方式，用于创建镜像效果。

-1：表示同时沿 x 轴和 y 轴翻转（水平和垂直都翻转，相当于旋转180度）。

dst: 输出图像，与输入图像有相同的大小和类型。这是一个可选参数，如果提供，则翻转的结果会存储在这个图像中；如果未提供，则会创建一个新的图像来存储结果。

python 复制代码 
# 对图像进行翻转操作
import cv2

# 1. 读取图片
image_np = cv2.imread('./lena.png')

# 2. 使用flip函数去对图像进行镜像的翻转
# cv2.flip： 对图像进行镜像翻转
# 第一个参数：要翻转的原始图像
# 第二个参数：标志位， 0：表示绕x轴进行上下翻转， >0:表示绕y轴进行左右翻转  <0:表示绕x轴和y轴各进行一次翻转
image_flip = cv2.flip(image_np, 0)

# 3. 输出，显示
cv2.imshow('image_np', image_np)
cv2.imshow('image_flip', image_flip)
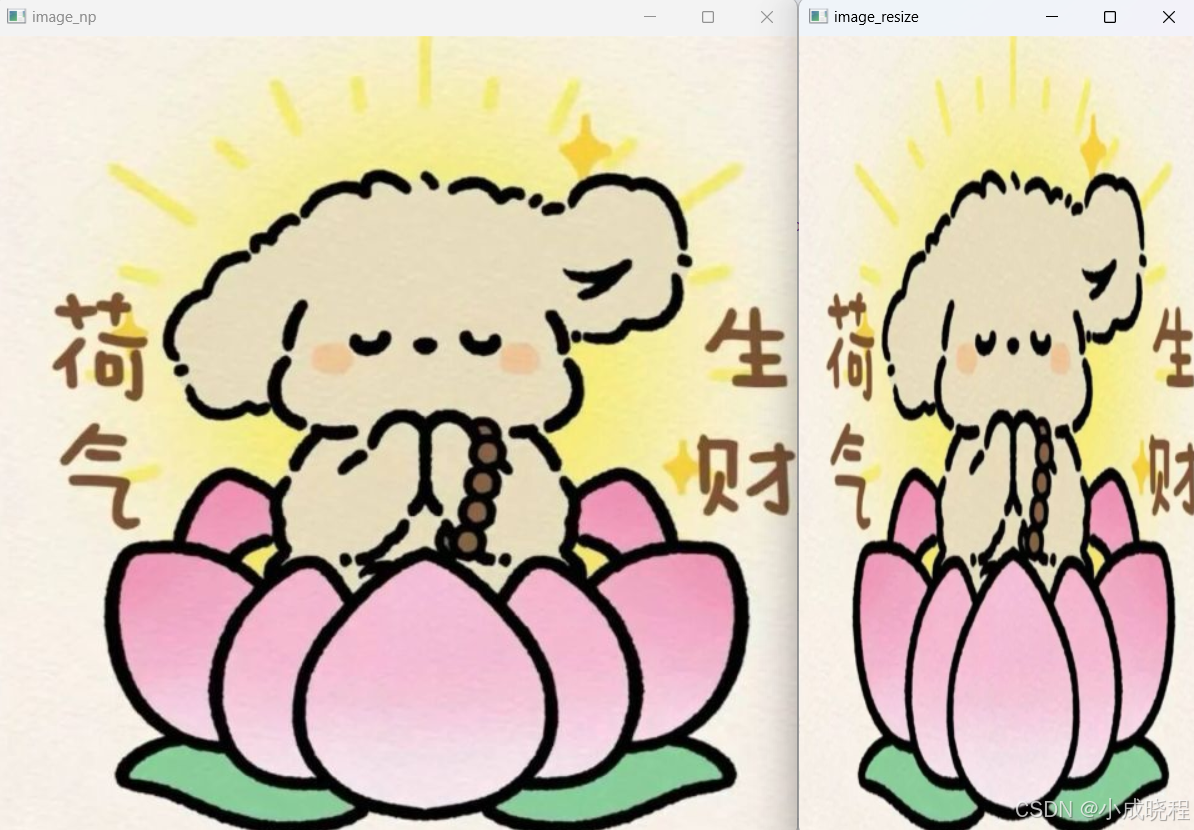
cv2.waitKey(0)

4、图像缩放

cv2.resize(src, dsize, dst=None, fx=None, fy=None, interpolation=cv2.INTER_LINEAR)

功能：用于调整图像大小的函数

参数：

src: 输入图像，即你想要调整大小的图像。

dsize: 输出图像的尺寸，以 (width, height) 的形式表示。如果指定了这个参数，那么 fx 和 fy 将被忽略。如果 dsize 是 (0, 0)，则必须指定 fx 和 fy。

dst: 输出图像，与输入图像有相同的数据类型和通道数。这是一个可选参数，如果提供，则调整大小后的结果会存储在这个图像中；如果未提供，则会创建一个新的图像来存储结果。

fx: 宽度方向的缩放因子。如果指定了这个参数，那么 dsize 的宽度将被忽略。如果 dsize 和 fx（或 fy）同时被指定，那么 dsize 将被用来计算输出图像的尺寸，而 fx（和 fy）将被忽略。

fy: 高度方向的缩放因子。它的作用与 fx 类似，但是是针对高度的。

interpolation: 插值方法，如 cv2.INTER_NEAREST（最近邻插值）、cv2.INTER_LINEAR（线性插值，默认值）、cv2.INTER_AREA（使用像素区域关系的一种重采样方法，可能更适合图像缩小）、cv2.INTER_CUBIC（4x4 像素邻域的双三次插值）等。

python 复制代码 
# 对图像进行翻转操作
import cv2

# 1. 读取图片
image_np = cv2.imread('../1iamge/011.jpg')


# 2. 图片缩放
# dsize和fx、fy不能同时使用，如果同时出现，会以dsize的标准进行缩放
# 如果想要使用resize函数，就必须填入两个参数：src和dsize
# 如果不想使用dsize，赋为None就行。
image_resize = cv2.resize(image_np, dsize=None, fx=0.5, fy=1, interpolation=cv2.INTER_LINEAR)

# 3. 显示图像
cv2.imshow('image_np', image_np)
cv2.imshow('image_resize', image_resize)
cv2.waitKey(0)

六、图像矫正

图像矫正的原理是透视变换，下面来介绍一下透视变换的概念。

听名字有点熟，我们在图像旋转里接触过仿射变换，知道仿射变换是把一个二维坐标系转换到另一个二维坐标系的过程，转换过程坐标点的相对位置和属性不发生变换，是一个线性变换，该过程只发生旋转和平移过程。因此，一个平行四边形经过仿射变换后还是一个平行四边形。

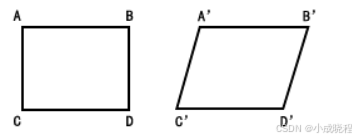
而透视变换是把一个图像投影到一个新的视平面的过程，在现实世界中，我们观察到的物体在视觉上会受到透视效果的影响，即远处的物体看起来会比近处的物体小。透视投影是指将三维空间中的物体投影到二维平面上的过程，这个过程会导致物体在图像中出现形变和透视畸变。透视变换可以通过数学模型来校正这种透视畸变，使得图像中的物体看起来更符合我们的直观感受。通俗的讲，透视变换的作用其实就是改变一下图像里的目标物体的被观察的视角。

|---|---|
| | |

如上图所示，左图在经过透视变换后得到了右图的结果，带入上面的话就是图像中的车道线（目标物体）的被观察视角从平视视角变成了俯视视角，这就是透视变换的作用。

其中x、y是原始图像点的坐标，x\^{\\prime}、y\^{\\prime}是变换后的坐标，a11，a12，...,a33则是一些旋转量和平移量，由于透视变换矩阵的推导涉及三维的转换，所以这里不具体研究该矩阵，只要会使用就行，而OpenCV里也提供了getPerspectiveTransform()函数用来生成该3*3的透视变换矩阵。

cv2.getPerspectiveTransform(src, dst)

功能：cv2.getPerspectiveTransform(src, dst)

参数：

src: 源图像中的四个点，通常是一个形状为 (4, 2) 的 numpy 数组或类似的数据结构，表示四个点的坐标。这四个点应该按照某种顺序排列（例如，顺时针或逆时针），因为变换矩阵的计算依赖于这个顺序。

dst: 目标图像中的四个点，与 src 参数类似，也是一个形状为 (4, 2) 的 numpy 数组或类似的数据结构，表示变换后四个点应该位于的位置。

函数返回一个 3x3 的变换矩阵，可以使用 cv2.warpPerspective() 函数将这个矩阵应用于图像，从而执行透视变换。
cv2.warpPerspective(src, M, dsize, dst=None, flags=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=None)

功能：用于对图像进行透视变换的函数

参数：

src: 输入图像，即你想要进行透视变换的源图像。

M: 透视变换矩阵，通常是一个 3x3 的矩阵，可以通过 cv2.getPerspectiveTransform() 函数计算得到。这个矩阵定义了源图像中的点如何映射到目标图像中的点。

dsize: 输出图像的尺寸，以 (width, height) 的形式表示。这是变换后图像的尺寸。

dst: 输出图像，这是一个可选参数。

flags: 插值方法。

borderMode: 边界填充方法。

borderValue: 边界颜色【可选】。

python 复制代码 
import  cv2
import numpy as np

# 1、读取一张图片
img = cv2.imread("./card.png")

# 2、 获取透视变换矩阵
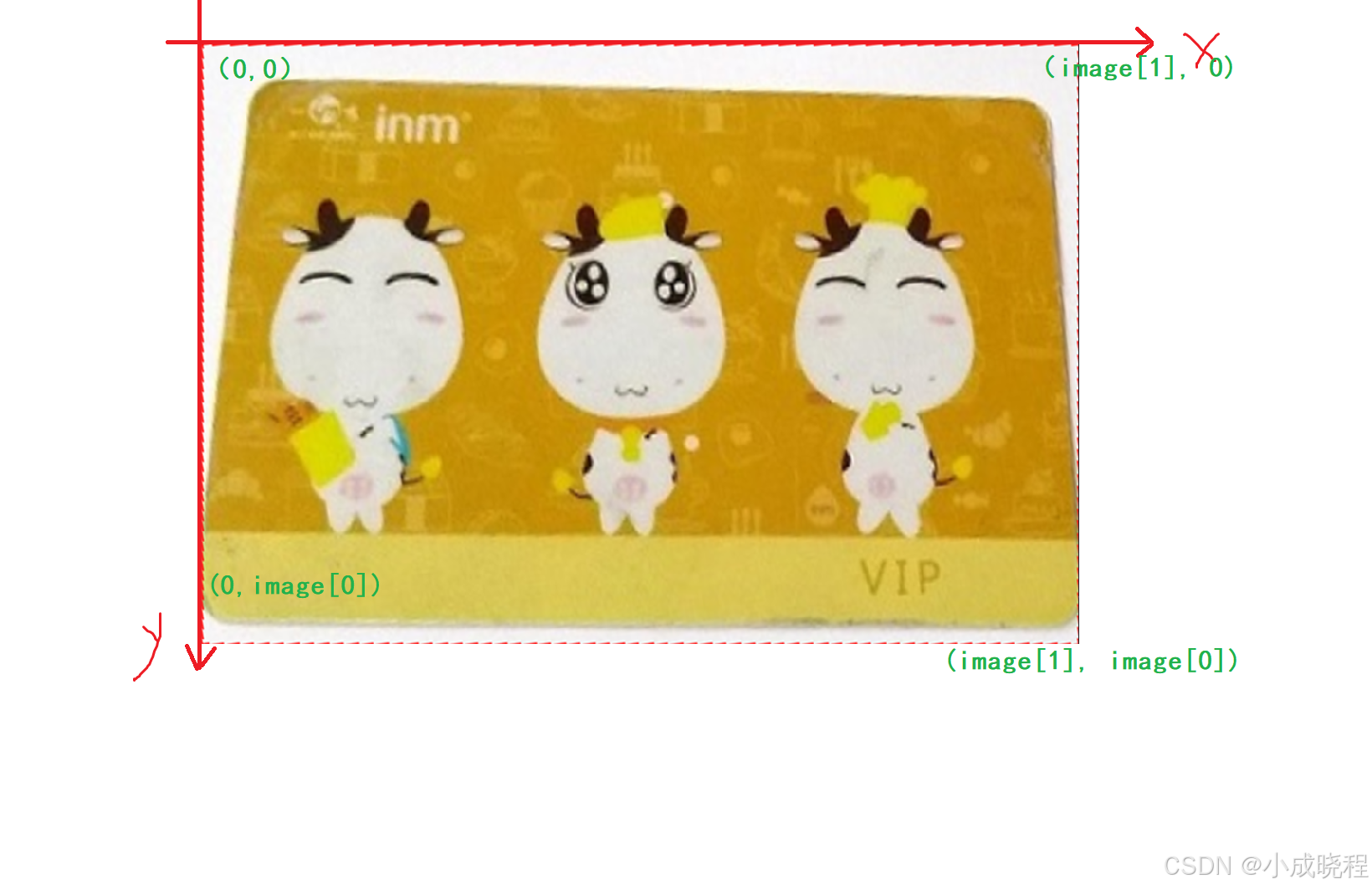
# 原图中的四个点
points1 = np.array([[226,126],[670,177],[140,400],[650,460]],dtype = np.float32)
# 目标图中的四个点
points2 = np.array([[0, 0], [img.shape[1], 0], [0, img.shape[0]], [img.shape[1], img.shape[0]]],dtype=np.float32)
M = cv2.getPerspectiveTransform(points1, points2)

# 3、透视变换
img_warp = cv2.warpPerspective(img, M, (img.shape[1], img.shape[0]))

cv2.imshow('image', img)
cv2.imshow('image_warp', img_warp)
cv2.waitKey(0)
相关推荐
菜狗woc1 小时前
opencv库中的函数应用
python·opencv·计算机视觉
Byron Loong1 小时前
Python+OpenCV系列：模版匹配
python·opencv·计算机视觉
带带老表学爬虫1 小时前
opencv滤波操作
人工智能·opencv·计算机视觉
GOTXX2 小时前
【自动驾驶】单目摄像头实现自动驾驶3D目标检测
图像处理·人工智能·python·目标检测·机器学习·3d·自动驾驶
WeeJot嵌入式2 小时前
卷积神经网络（CNNs）：图像识别的超级英雄
深度学习·神经网络·计算机视觉
有Li3 小时前
MedLSAM: 用于3D CT图像的局部化和分割模型|文献速递-生成式模型与transformer在医学影像中的应用
人工智能·计算机视觉·目标跟踪
飞飞-躺着更舒服13 小时前
多媒体文件解复用（Demuxing）过程
计算机视觉·音视频
OCR的搬砖小能手15 小时前
光学字符识别（OCR）技术：数字化浪潮中的关键力量
人工智能·计算机视觉·ocr
十有久诚15 小时前
SPT: Revisiting the Power of Prompt for Visual Tuning
人工智能·深度学习·计算机视觉·提示学习
热门推荐
01(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明02【halcon】halcon字符识别——OCR03玄机平台应急响应—webshell查杀04【一文读懂】NTN（非地面网络）技术介绍0504 - matlab m_map地学绘图工具基础函数 - 设置网格06Docker 夺命连环 15 问07『手写ahooks系列-useClickAway』一个hook解决监听点击元素外部08支付宝短视频平台创作分成激励项目09PyTorch机器学习实现液态神经网络10校验 GPT-4 真实性的三个经典问题：快速区分 GPT-3.5 与 GPT-4，并提供免费测试网站