本文介绍不依赖贝塞尔曲线,如何绘制一条平滑曲线,用于解决无贝塞尔控制点的情况下绘制曲线、但数据点不在贝塞尔曲线的场景。
在上一家公司我做过一个平滑曲线编辑工具,用于轮椅调整加减速曲线。基于几个用户可控制的点,生成一条平滑的曲线,控制点需要保持在曲线上。
今天和小伙伴沟通,白板的形状绘制笔迹,也可以使用到这个技术,所以需要回顾总结下
贝塞尔平滑曲线
我们先讲贝塞尔曲线GDI+ 中的贝塞尔自由绘制曲线 - Windows Forms .NET Framework | Microsoft Learn。一般情况我们绘制平滑曲线,直接以贝塞尔曲线API将多个点作为参数,直接进行绘制。这种情况下API会自动将第一个点作为控制点,得到贝塞尔曲线,比如下面生成一条平滑Geometry:
1 var geometryTest = new StreamGeometry();
2 using(var ctx = geometryTest.Open())
3 {
4 ctx.BeginFigure(_points[0], true, false);
5 if(keyPoints.Count % 2 == 0)
6 {
7 //绘制二阶贝塞尔函数,需要保证为偶数点
8 ctx.PolyQuadraticBezierTo(keyPoints, true, true);
9 }
10 else
11 {
12 //绘制二阶贝塞尔函数,需要保证为偶数点
13 keyPoints.Insert(0, keyPoints[0]);
14 ctx.PolyQuadraticBezierTo(keyPoints, true, true);
15 }
16 }这里的PolyQuadraticBezierTo函数,塞点集列表进去并设置平滑参数isSmoothJoin=true
1 public abstract void PolyQuadraticBezierTo(
2 IList<Point> points,
3 bool isStroked,
4 bool isSmoothJoin);
5
6 public abstract void PolyBezierTo(IList<Point> points, bool isStroked, bool isSmoothJoin);官网有介绍,列表中第一个点作为控制点:StreamGeometryContext.PolyQuadraticBezierTo 方法 (System.Windows.Media) |Microsoft 学习
上面是自动设置控制点,这类实现方案会有一个问题:数据点最终可能不在曲线上
基于贝塞尔曲线,我们也可以计算控制点。但计算控制点,也是同样无法保证原始数据点会在拟合后的曲线上。
模拟平滑曲线
以现有数据点,如果直接相连肯定只会生成多个折线。如果我们添加多个点,可以模拟一条类似曲线路径的多边形近似点集,与Geometry下的FlattenedPathGeometry有点类似。
方案一,可以使用MathNet.Numerics生成一条X方向的N阶曲线,然后输入X坐标输出Y坐标,得到曲线上的点。 MathNet.Numerics可以参考 .NET 白板书写加速-曲线拟合预测 - 唐宋元明清2188 - 博客园。但这方案会生成无数点,曲线绘制性能无法得到保证。所以添加这些曲线路径的点,如何以最小的点集实现?可以对相邻点,对向量角度变化以及相邻间距设置一个最小阈值,最终得到符合的点集
方案二,用我之前实现方案,根据最简多项式代码算出近似样条曲线点集。原理同MathNet.Numerics里的Polynomial函数,下面是部分代码:
1 private const double Tolerance = 0.5;
2
3 /// <summary>
4 /// 获取拟合后的点集
5 /// </summary>
6 /// <param name="points"></param>
7 /// <returns></returns>
8 public static List<Point> GetFittingLinePoints(List<Point> points)
9 {
10 var orderedPoints = (from pt in points orderby pt.X select pt).ToList();
11 var secondDerivatives = SecondDerivativeHelper.GetSecondDerivatives(orderedPoints);
12 List<Point> polyLinePoints = PointFakeApproximationHelper.GetSplinePolyLineApproximation(orderedPoints, secondDerivatives, Tolerance);
13 return polyLinePoints;
14 }获取俩点之间点集:
1 /// <summary>
2 /// 用折线逼近三次多项式并给出公差。
3 /// </summary>
4 /// <param name="leftPoint">三次多项式左点</param>
5 /// <param name="rightPoint">三次多项式右点</param>
6 /// <param name="secondDerivativeLeft">左点三次多项式二阶导数.</param>
7 /// <param name="secondDerivativeRight">右端三次多项式二阶导数.</param>
8 /// <param name="tolerance">公差,即样条到近似折线的最大距离。</param>
9 /// <returns>在给定公差的情况下逼近三次多项式的多边形点的列表。</returns>
10 private static Collection<Point> GetApproximation(Point leftPoint, Point rightPoint, double secondDerivativeLeft, double secondDerivativeRight, double tolerance)
11 {
12 // 左右俩点的X、Y轴值
13 double leftPointX = leftPoint.X, rightPointX = rightPoint.X;
14 double leftPointY = leftPoint.Y, rightPointY = rightPoint.Y;
15 // 次区间多项式系数
16 double a = (secondDerivativeRight - secondDerivativeLeft) / (6 * (rightPointX - leftPointX));
17 double b = (secondDerivativeLeft - 6 * a * leftPointX) / 2;
18 double c = (rightPointY - rightPointX * rightPointX * (a * rightPointX + b) - leftPointY + leftPointX * leftPointX * (a * leftPointX + b)) / (rightPointX - leftPointX);
19 double d = leftPointY - leftPointX * (leftPointX * (a * leftPointX + b) + c);
20
21 //如果a的值为0,则给a赋值double类型的最小正数
22 if(a == 0)
23 a = double.Epsilon;
24
25 //通过多项式与拆线的逼近,获取多边形点的列表
26 Collection<Point> points = CubicPolynomialPolylineApproximation.Approximate(new Polynomial(new double[] { d, c, b, a }), leftPointX, rightPointX, tolerance);
27 return points;
28 }效果如下图,左侧是原数据点集(绿色),右则截图是模拟后的点集显示(红色):

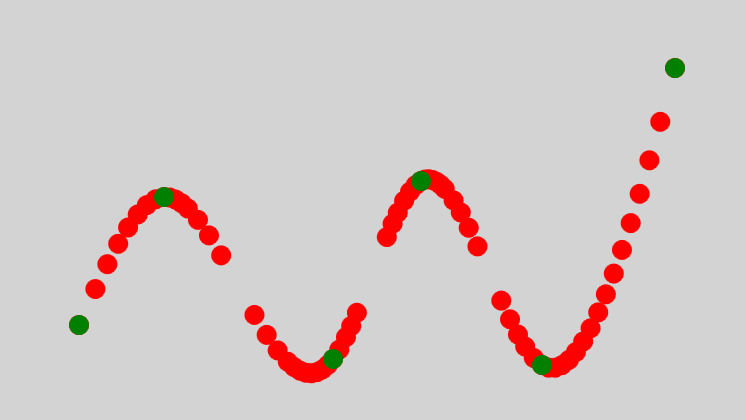
把这些新增点与原数据点,用直接连接起来,就是一条比较平滑的曲线了。同时原数据点也在拟合的曲线上。另外,如果还需要优化下这些线段的平滑,可以使用贝塞尔曲线替换直线连接,已经加了很多密集点,绿点不会脱离曲线的。
Github仓库代码 GitHub - kybs00/CurveLineEditDemo: 平滑曲线模拟及编辑Demo
编辑平滑曲线
上面我们已经完成了平滑曲线的点集模拟,连接起来就是一条曲线。在一些业务场景中,需要以曲线上的点为控制操作点,移动点以达到编辑曲线。
在曲线上设置多个操作点。如何在曲线上设置期望位置的点,可以看 .NET 曲线上的点- 获取距离最近的点 - 唐宋元明清2188 - 博客园。点击时,获取曲线离点击位置最近的点即可
选择点后,操作控制点移动。曲线根据操作点的位置变更,重新生成新的曲线。曲线编辑效果如下图:
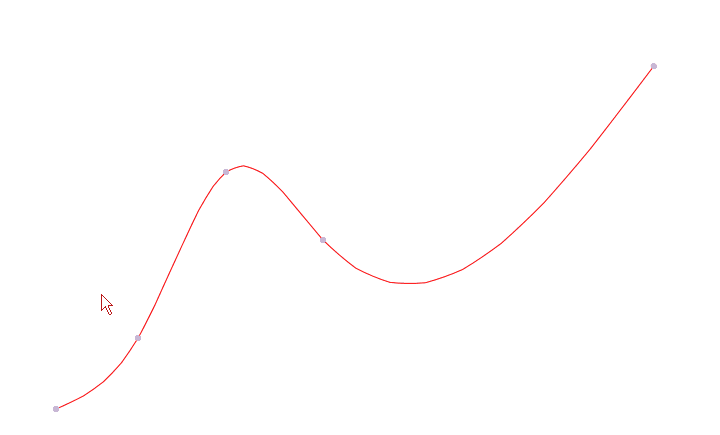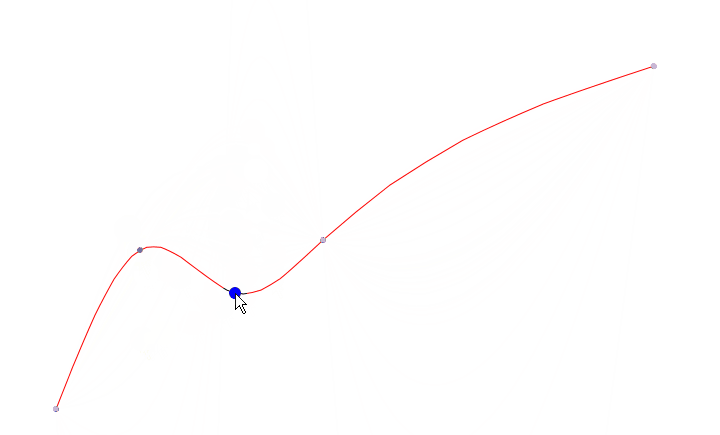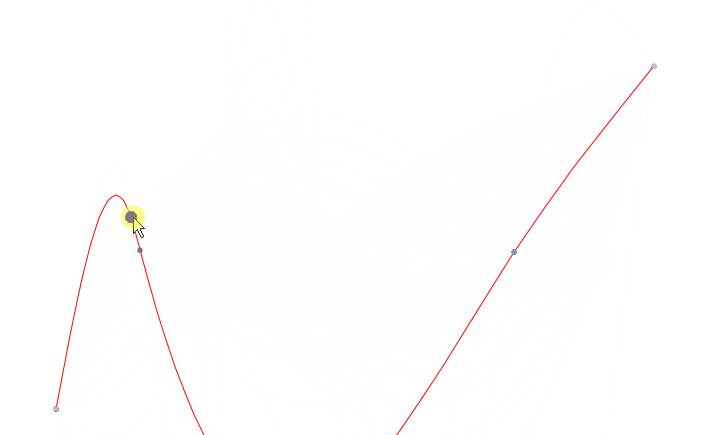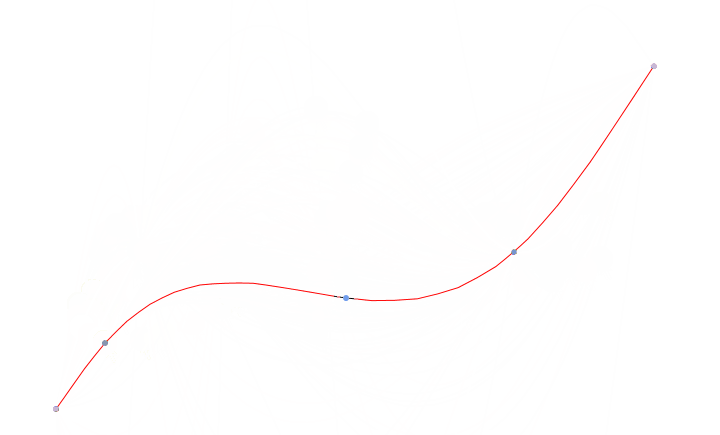
重新生成曲线这部分代码没有啥难点,核心代码就是上面的平滑曲线模拟。看上面仓库代码即可
参考文章:
GDI+ 中的贝塞尔自由绘制曲线 - Windows Forms .NET Framework | Microsoft Learn