Leecode刷题C语言之k次乘运算后的数组②

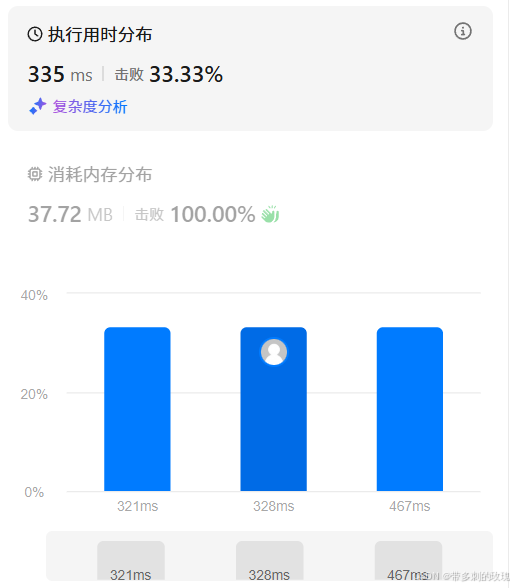
执行结果:通过

执行用时和内存消耗如下：

#define MIN_QUEUE_SIZE 64

typedef struct Element {
    long long val;
    int idx;
} Element;

typedef bool (*compare)(const void *, const void *);

typedef struct PriorityQueue {
    Element *arr;
    int capacity;
    int queueSize;
    compare lessFunc;
} PriorityQueue;

static bool less(const void *a, const void *b) {
    Element *e1 = (Element *)a;
    Element *e2 = (Element *)b;
    return e1->val > e2->val || \
           (e1->val == e2->val && \
           e1->idx > e2->idx);
}

static void memswap(void *m1, void *m2, size_t size){
    unsigned char *a = (unsigned char*)m1;
    unsigned char *b = (unsigned char*)m2;
    while (size--) {
        *b ^= *a ^= *b ^= *a;
        a++;
        b++;
    }
}

static void swap(Element *arr, int i, int j) {
    memswap(&arr[i], &arr[j], sizeof(Element));
}

static void down(Element *arr, int size, int i, compare cmpFunc) {
    for (int k = 2 * i + 1; k < size; k = 2 * k + 1) {
        if (k + 1 < size && cmpFunc(&arr[k], &arr[k + 1])) {
            k++;
        }
        if (cmpFunc(&arr[k], &arr[(k - 1) / 2])) {
            break;
        }
        swap(arr, k, (k - 1) / 2);
    }
}

PriorityQueue *createPriorityQueue(compare cmpFunc) {
    PriorityQueue *obj = (PriorityQueue *)malloc(sizeof(PriorityQueue));
    obj->capacity = MIN_QUEUE_SIZE;
    obj->arr = (Element *)malloc(sizeof(Element) * obj->capacity);
    obj->queueSize = 0;
    obj->lessFunc = cmpFunc;
    return obj;
}

void heapfiy(PriorityQueue *obj) {
    for (int i = obj->queueSize / 2 - 1; i >= 0; i--) {
        down(obj->arr, obj->queueSize, i, obj->lessFunc);
    }
}

void enQueue(PriorityQueue *obj, Element *e) {
    // we need to alloc more space, just twice space size
    if (obj->queueSize == obj->capacity) {
        obj->capacity *= 2;
        obj->arr = realloc(obj->arr, sizeof(Element) * obj->capacity);
    }
    memcpy(&obj->arr[obj->queueSize], e, sizeof(Element));
    for (int i = obj->queueSize; i > 0 && obj->lessFunc(&obj->arr[(i - 1) / 2], &obj->arr[i]); i = (i - 1) / 2) {
        swap(obj->arr, i, (i - 1) / 2);
    }
    obj->queueSize++;
}

Element* deQueue(PriorityQueue *obj) {
    swap(obj->arr, 0, obj->queueSize - 1);
    down(obj->arr, obj->queueSize - 1, 0, obj->lessFunc);
    Element *e =  &obj->arr[obj->queueSize - 1];
    obj->queueSize--;
    return e;
}

bool isEmpty(const PriorityQueue *obj) {
    return obj->queueSize == 0;
}

Element* front(const PriorityQueue *obj) {
    if (obj->queueSize == 0) {
        return NULL;
    } else {
        return &obj->arr[0];
    }
}

void clear(PriorityQueue *obj) {
    obj->queueSize = 0;
}

int size(const PriorityQueue *obj) {
    return obj->queueSize;
}

void freeQueue(PriorityQueue *obj) {
    free(obj->arr);
    free(obj);
}

long long quickMul(long long x, long long y, long long m) {
    long long res = 1;
    while (y) {
        if (y & 1) {
            res = (res * x) % m;
        }
        y >>= 1;
        x = (x * x) % m;
    }
    return res;
}

int* getFinalState(int* nums, int numsSize, int k, int multiplier, int* returnSize) {
    *returnSize = numsSize;
    if (multiplier == 1) {
        return nums;
    }
    long long n = numsSize, m = 1e9 + 7;
    long long mx = 0;
    for (int i = 0; i < numsSize; i++) {
        mx = fmax(mx, nums[i]);
    }
    
    PriorityQueue *v = createPriorityQueue(less);
    Element e;
    for (int i = 0; i < n; i++) {
        e.val = nums[i];
        e.idx = i;
        enQueue(v, &e);
    }
    while (k > 0 && front(v)->val < mx) {
        e.val = front(v)->val * multiplier;
        e.idx = front(v)->idx;
        deQueue(v);
        enQueue(v, &e);
        k--;
    }    
    for (int i = 0; i < n; i++) {
        long long val = front(v)->val;
        int idx = front(v)->idx;
        deQueue(v);
        int t = k / n + (i < k % n);
        nums[idx] = ((val % m) * quickMul(multiplier, t, m)) % m;
    }
    freeQueue(v);
    return nums;
}

解题思路：

以下是对提供的代码进行详细解析的思路分析：

核心数据结构：优先级队列（PriorityQueue）

定义：
- 结构体 Element 储存一个长整型值 val 和一个整型索引 idx。
- 结构体 PriorityQueue 包含：
  - 一个 Element 类型的数组 arr。
  - 队列的容量 capacity 和当前大小 queueSize。
  - 一个指向比较函数的指针 lessFunc，用于元素间的比较。
比较函数 ：
- less 函数：用于确定两个 Element 的大小关系，首先根据 val 值进行比较，若相同则比较 idx 值。该函数被设计为用于最大堆（根节点值最大）。
辅助函数 ：
- memswap 和 swap：用于交换两个 Element 或内存块。
- down：堆化函数，用于调整子树以维持最大堆的性质。
队列操作 ：
- createPriorityQueue：创建并初始化一个优先级队列。
- heapify：将一个无序数组转换为最大堆。
- enQueue：向队列中添加一个元素，并调整堆结构。
- deQueue：移除并返回堆顶元素，同时调整堆结构。
- isEmpty、front、clear、size 和 freeQueue：用于检查队列是否为空、获取堆顶元素、清空队列、获取队列大小和释放队列内存。

主要功能函数：`getFinalState`

目标：
- 给定一个整数数组 nums、数组大小 numsSize、操作次数 k 和乘数 multiplier，通过特定规则更新数组并返回。
实现逻辑 ：
- 首先处理特殊情况：若 multiplier 为 1，则数组无需更新，直接返回。
- 计算数组中的最大值 mx，用于后续判断。
- 创建一个优先级队列 v，并将数组 nums 中的元素作为 Element 对象加入队列。
- 循环处理：只要 k 大于 0 且堆顶元素小于 mx，则取出堆顶元素，乘以 multiplier 后重新加入队列。此步骤模拟对数组中最小元素的乘法操作。
- 最后，遍历优先级队列，计算每个元素在 k 次操作后的值。若元素在剩余操作中被多次选择，则使用 quickMul 函数（快速幂算法）计算其最终值。注意，结果需要对 1e9 + 7 取模以避免溢出。
- 释放优先级队列的内存。
关键细节 ：
- 使用优先级队列来高效地找到并更新最小元素。
- 通过快速幂算法 quickMul 优化大数乘法，同时保持结果的模运算。
- 在计算最终状态时，根据元素在剩余操作中的选择次数进行相应调整。

总结

提供的代码实现了一个基于优先级队列（最大堆）的算法，用于模拟对整数数组中的最小元素进行 k 次乘法操作，并计算每个元素在 k 次操作后的值（考虑乘数和模运算）。该算法利用最大堆快速找到并更新最小元素，同时利用快速幂算法优化乘法运算。

Leecode刷题C语言之k次乘运算后的数组②

核心数据结构：优先级队列（PriorityQueue）

主要功能函数：getFinalState

总结

主要功能函数：`getFinalState`