目录
[六、封装 map 和 set](#六、封装 map 和 set)
[1、封装 map](#1、封装 map)
[2、封装 set](#2、封装 set)
一、红黑树的定义
红黑树,是一种二叉搜索树,但添加了 '红' 和 '黑' 两种颜色标记位。
红黑树的最长路径最短是最短路径的二倍,它不像 AVL树一样,它不是严格的平衡树。
二、红黑树的规则
1、根节点必须是黑的
2、不能有连续的红色节点
3、每条路径上的黑色节点的数量是相同的
通过这三条规则的约束,我们可以知道:最短路径是全黑,最长路径是一黑一红交替。
也就是最长路径是最短路径的 2 倍。
示例:
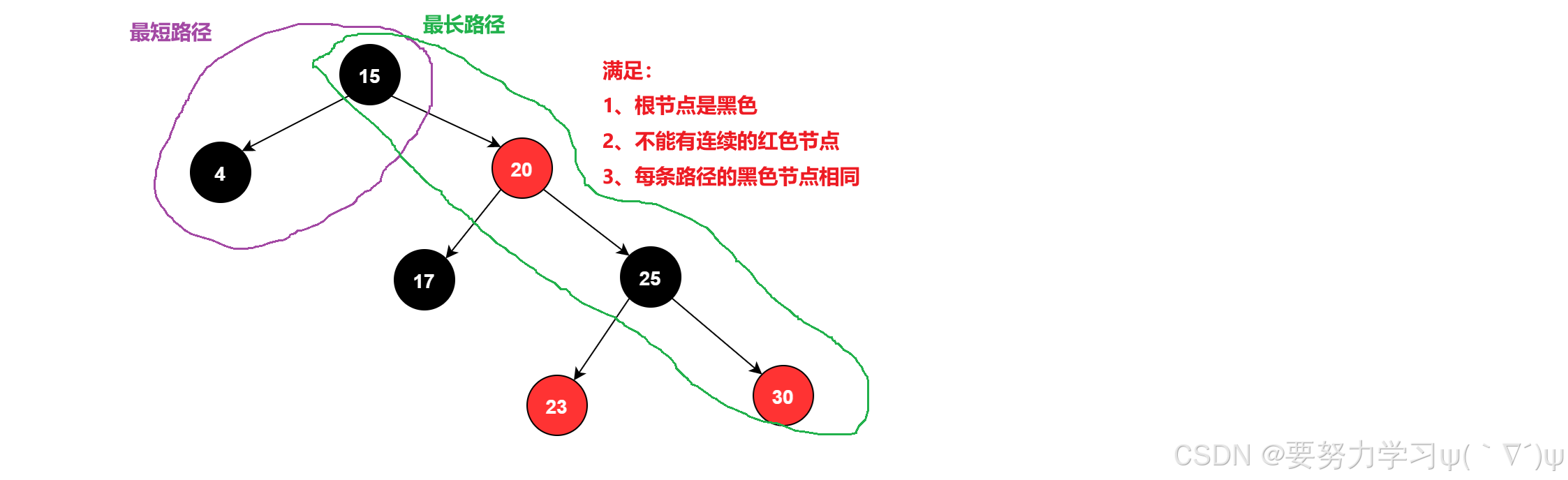
三、红黑树的插入
新插入的节点一定为红色,因为插入黑色节点不好控制 '每条路径黑色节点相同' 这条规则
红黑树的插入分为以下几种情况:
1、父节点为黑色,未违反规则,插入成功。
2、父节点为红色,出现连续的红色节点,我们需要进行修正
a、cur 为红,parent 为红,uncle 存在且为红
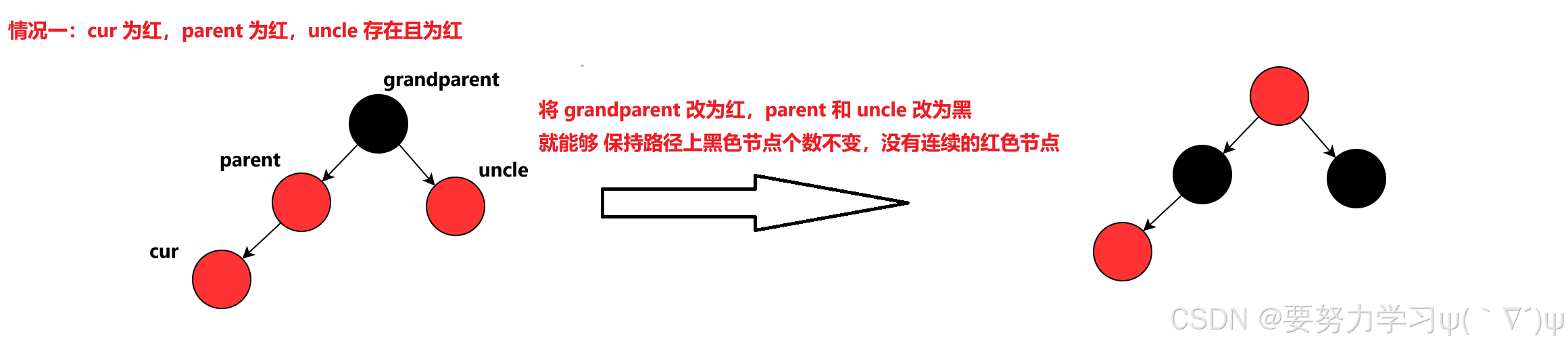
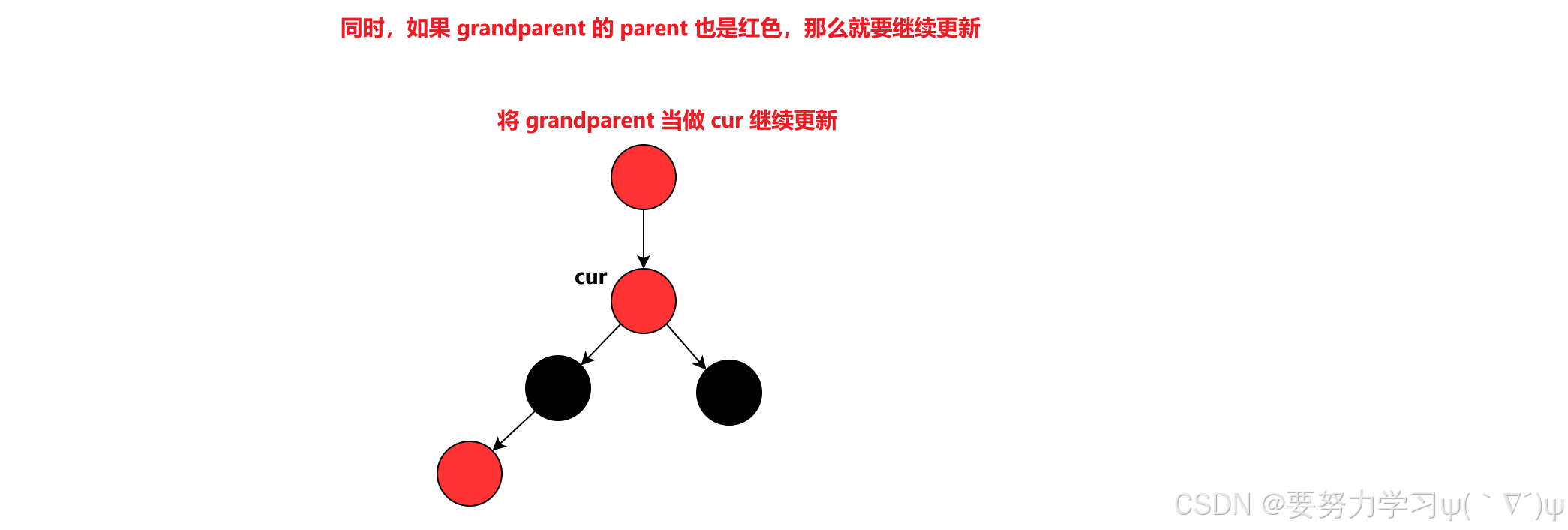
b、cur 为红,parent 为红,uncle 不存在或 uncle 为黑色
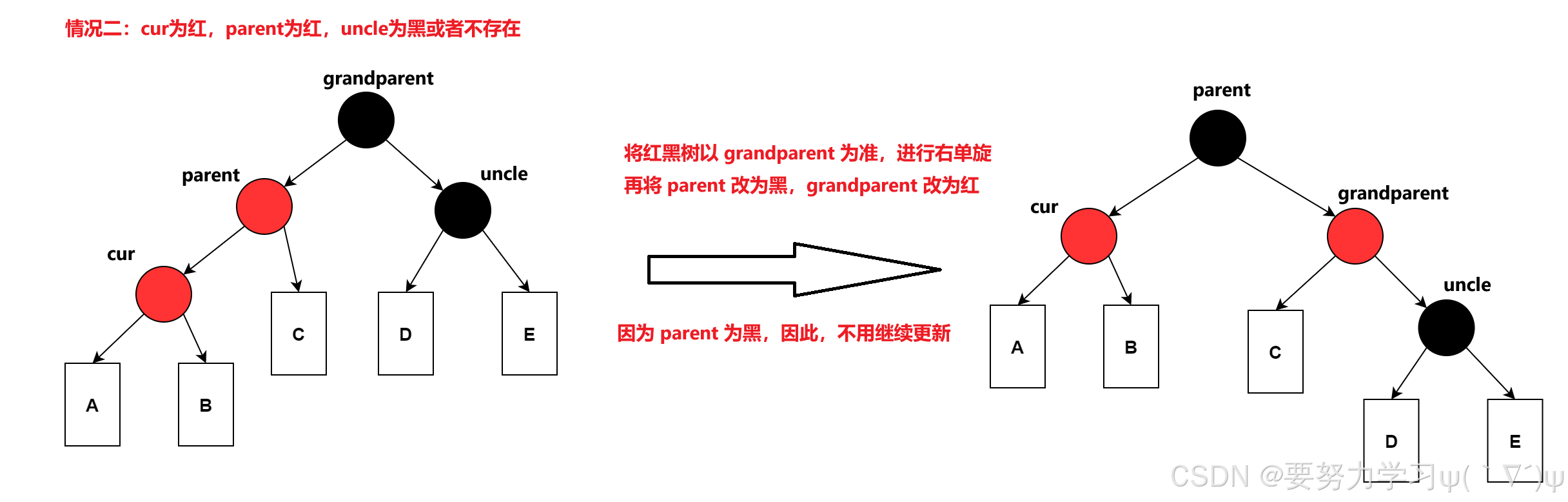
c、cur 为红,cur 在 parent 的右边,parent 为红,uncle 不存在或 uncle 为黑色
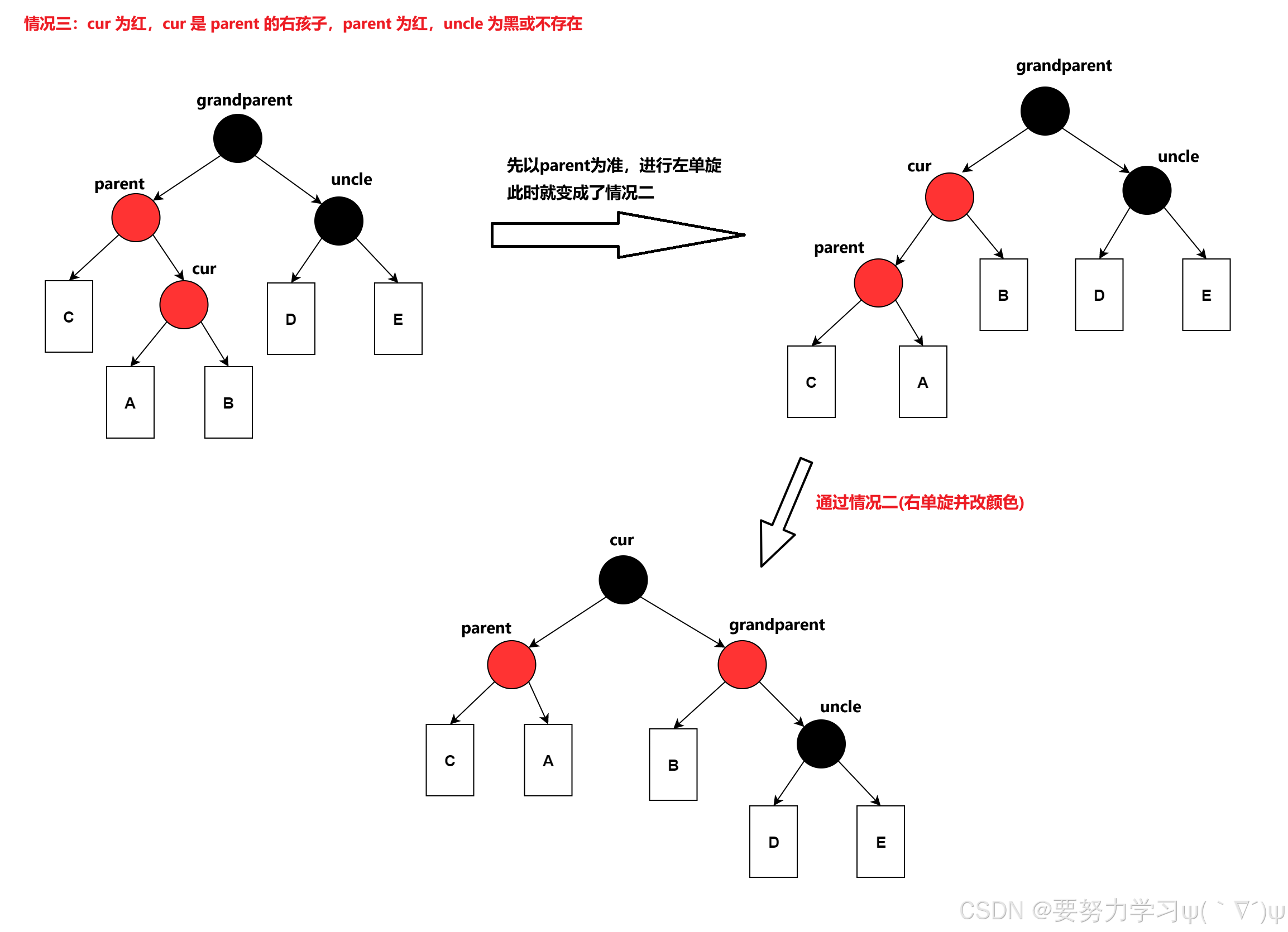
还有 parent 在 grandparent 右边的情况,与 b 和 c 类似。
在 a、b、c 三种情况中,只有 a 可能要继续更新,因为 a 中,把 grandparent 改为了红色。
而在 b、c 中,最上层节点为黑色,因此不需要继续更新。
具体实现如下:
红黑树节点:
cpp
// 枚举类型做颜色标记
enum Color
{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
std::pair<K, V> _val; // 存的值
Color _col; // 颜色标记
RBTreeNode* _left; // 左节点
RBTreeNode* _right; // 右节点
RBTreeNode* _parent; // 父节点
// 构造
RBTreeNode(const std::pair<K, V>& val)
:_val(val)
, _col(RED)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
{}
};红黑树的实现(插入):
cpp
template<class K, class V>
class RBTree
{
using node = RBTreeNode<K, V>;
public:
// 右单旋
void RotateR(node* cur)
{
node* parent = cur->_parent;
node* subL = cur->_left;
node* subR = cur->_right;
node* subLR = subL->_right;
subL->_right = cur;
cur->_left = subLR;
if(subLR)
subLR->_parent = cur;
cur->_parent = subL;
subL->_parent = parent;
// 若 cur 为根节点,就要更新根节点
if (cur == _root)
{
_root = subL;
}
else
{
if (parent->_left == cur)
parent->_left = subL;
else
parent->_right = subL;
}
}
// 左单旋
void RotateL(node* cur)
{
node* parent = cur->_parent;
node* subL = cur->_left;
node* subR = cur->_right;
node* subRL = subR->_left;
subR->_left = cur;
cur->_right = subRL;
if(subRL)
subRL->_parent = cur;
cur->_parent = subR;
subR->_parent = parent;
// 若 cur 为根节点,就要更新根节点
if (cur == _root)
{
_root = subR;
}
else
{
if (parent->_left == cur)
parent->_left = subR;
else
parent->_right = subR;
}
}
bool Insert(const std::pair<K, V>& val)
{
// 如果 root 为空,直接 new 然后返回即可
if (_root == nullptr)
{
_root = new node(val);
_root->_col = BLACK;
return true;
}
// 找新节点该插入的位置
node* cur = _root;
node* parent = _root;
while (cur)
{
if (val.first > cur->_val.first)
{
// 新节点的值比当前节点的大,向右找
parent = cur;
cur = cur->_right;
}
else if (val.first < cur->_val.first)
{
// 新节点的值比当前节点的小,向左找
parent = cur;
cur = cur->_left;
}
else
{
// 有相等的值,插入失败
return false;
}
}
cur = new node(val);
if (val.first < parent->_val.first)
{
// 新节点的值比父节点小,在左边
parent->_left = cur;
cur->_parent = parent;
}
else
{
// 新节点的值比父节点大,在右边
parent->_right = cur;
cur->_parent = parent;
}
// 改颜色
while (parent && parent->_col == RED)
{
node* grandparent = parent->_parent;
node* uncle = grandparent->_right;
if (grandparent->_right == parent)
uncle = grandparent->_left;
if (uncle && uncle->_col == RED)
{
// 叔叔存在且为红
grandparent->_col = RED;
parent->_col = BLACK;
uncle->_col = BLACK;
cur = grandparent;
parent = cur->_parent;
}
else
{
// 叔叔不存在 或 为黑
// parent 在 grandparent 左边
if (grandparent->_left == parent)
{
// cur 和 parent 都在左边,右单旋
// g
// p u
// c
if (parent->_left == cur)
{
RotateR(grandparent);
parent->_col = BLACK;
grandparent->_col = RED;
}
else
{
// parent 在左,cur 在右
// g
// p u
// c
// 先左单旋,再右单旋
RotateL(parent);
RotateR(grandparent);
grandparent->_col = RED;
cur->_col = BLACK;
}
}
else
{
// parent 在右边
if (parent->_right == cur)
{
// cur 和 parent 都在右边,左单旋
// g
// u p
// c
RotateL(grandparent);
parent->_col = BLACK;
grandparent->_col = RED;
}
else
{
// parent 在右,cur 在左
// g
// u p
// c
// 先右单旋,再左单旋
RotateR(parent);
RotateL(grandparent);
grandparent->_col = RED;
cur->_col = BLACK;
}
}
break;
}
}
_root->_col = BLACK;
return true;
}
private:
node* _root = nullptr;
};检查:
cpp
// 查看是否出现连续的红色节点
bool CheckRedNodes(node* cur)
{
if (cur == nullptr)
return true;
if (cur->_col == RED && cur->_parent->_col == RED)
{
cout << cur->_val.first << " 出现连续的红色节点\n";
return false;
}
return CheckRedNodes(cur->_left) && CheckRedNodes(cur->_right);
}
// 查看每条路径上的黑色节点个数
bool CheckPath(node* cur, int BNum, int& pivot)
{
if (cur == nullptr)
return true;
if (cur->_col == BLACK) BNum++;
if (cur->_left == nullptr && cur->_right == nullptr)
{
if (pivot == 0)
{
pivot = BNum;
cout << "每条路径黑色节点个数: " << BNum << endl;
return true;
}
else
{
if (BNum != pivot)
{
cout << cur->_val.first << "黑色节点个数不符合\n";
}
return BNum == pivot;
}
}
return CheckPath(cur->_left, BNum, pivot)
&& CheckPath(cur->_right, BNum, pivot);
}
// 检查红黑树是否正确
bool IsBalance()
{
if (_root && _root->_col == RED)
{
cout << " 根节点为红色,错误\n";
return false;
}
int pivot = 0;
return CheckRedNodes(_root)
&& CheckPath(_root, 0, pivot);
}四、红黑树的迭代器
迭代器就是像指针一样使用,我们只需要将 红黑树的节点 封装一下,完成运算符的重装即可
重点:
迭代器++:红黑树的迭代器++就是找中序的下一个节点。
找中序的下一个节点分为两种情况
1、右子树不为空,直接找到右子树的最左节点,就是中序的下一个位置
因为中序是 左 根 右,根走完了,右不为空,就找右的最左节点
2、右子树为空,向上找 左孩子的祖先
因为 左 根 右,右为空说明走完了,就要找左走完了的根,也就是向上找 cur 是 parent 的左孩子的节点,parent 就是下一个节点
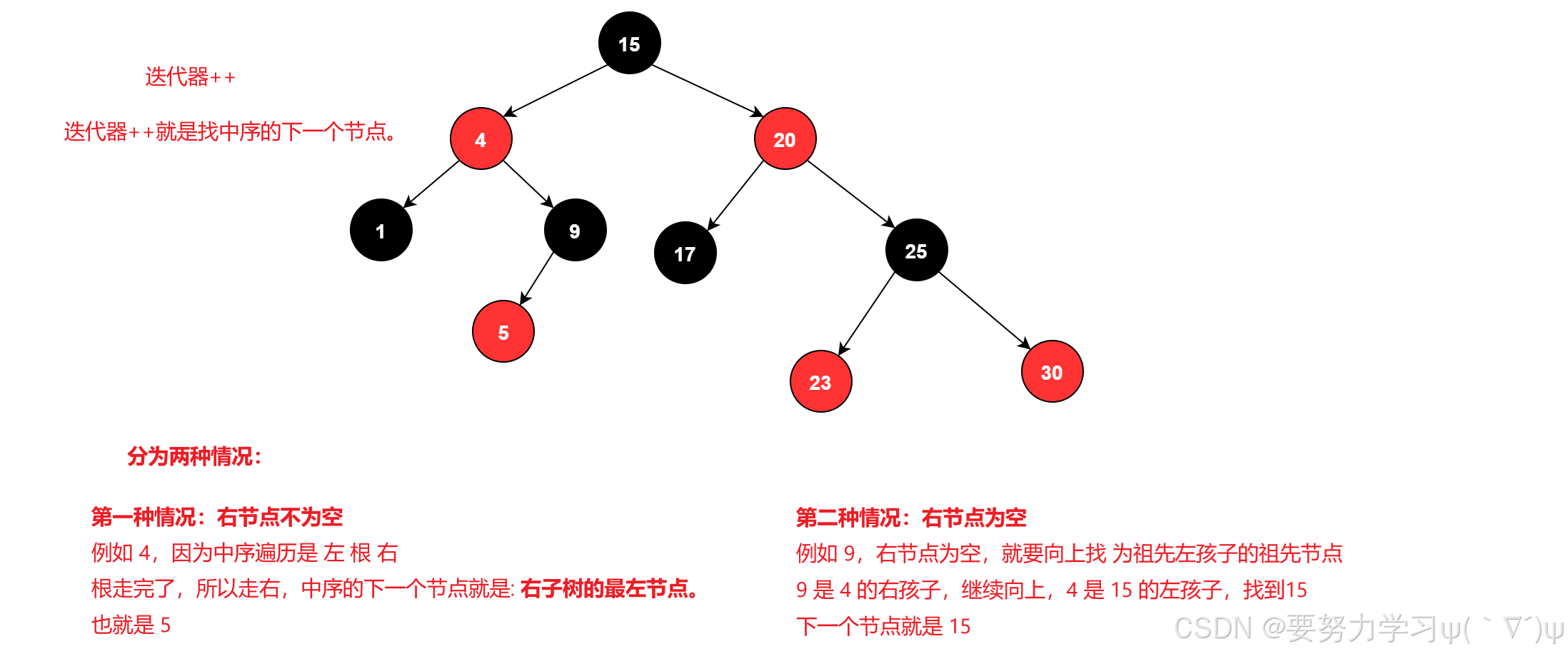
代码实现:
cpp
template<class T>
class _RBTree_Itreator
{
// 对红黑树节点重命名,防止名字太长
typedef RBTreeNode<T> node;
// 对迭代器自己重命名,防止名字太长
typedef _RBTree_Itreator<T> self;
public:
// 构造函数,用节点指针构造迭代器
_RBTree_Itreator(node* node)
:_node(node)
{}
// 重载解引用 *
T& operator*()
{
return _node->_val;
}
// 重载箭头 ->
T* operator->()
{
return &_node->_val;
}
// 重装 不等于!= ,判断两个迭代器是否相等
bool operator!=(const self& it)
{
return _node != it._node;
}
// 重载前置++,++iterator
self& operator++()
{
if (_node->_right)
{
// 如果右子树存在,就找右子树的最左节点
node* cur = _node->_right;
while (cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else
{
// 右子树不存在,找 左孩子的祖先
node* cur = _node;
node* parent = cur->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
private:
node* _node;// 红黑树节点
};五、添加模版参数
1、将 V 改为 T,T 表示具体存的类型
我们之前是针对 map 实现的红黑树,因为 map 才存的是 pair,Set 存的是K,为了让 set 也可以复用同一棵树,我们将第二个参数 V 改为 T,T 表示具体存的类型
例如:在map<string, int>中,T 存的是 pair<string, int>. 而在 set<int> 中,存的是 int
2、添加模版参数 KOfT
KOfT:通过 T 拿到对应的 key。
因为 map 存的是pair ,而 set 是直接存 K,因此,我们需要通过回调仿函数拿到 K 来控制
为了完成 set 和 map 的封装,实现通过同一个红黑树复用,添加模版参数 KOFT
比如 set<int>,key 和 T 都是 int;但 map<string, int> key 是 string 而 T 是 pair<string, int>.
3、Compare:传入比较的参数
比如:set<Date> Date 是自定义的日期类,我们得传入比较参数才知道该如何比较。
因此,我们需要对上面的红黑树的代码进行修改,在拿到 key 的地方不能直接用 .first ,而应该用 KOfT,在比较的地方用 Compare。
修正后的完整代码
cpp
// 枚举类型做颜色标记
enum Color
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
T _val; // 存的值
Color _col; // 颜色标记
RBTreeNode* _left; // 左节点
RBTreeNode* _right; // 右节点
RBTreeNode* _parent; // 父节点
// 构造
RBTreeNode(const T& val)
:_val(val)
, _col(RED)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
{}
};
// 迭代器
template<class T>
class _RBTree_Itreator
{
// 对红黑树节点重命名,防止名字太长
typedef RBTreeNode<T> node;
// 对迭代器自己重命名,防止名字太长
typedef _RBTree_Itreator<T> self;
public:
// 构造函数,用节点指针构造迭代器
_RBTree_Itreator(node* node)
:_node(node)
{}
// 重载解引用 *
T& operator*()
{
return _node->_val;
}
// 重载箭头 ->
T* operator->()
{
return &_node->_val;
}
// 重装 不等于!= ,判断两个迭代器是否相等
bool operator!=(const self& it)
{
return _node != it._node;
}
// 重载前置++,++iterator
self& operator++()
{
if (_node->_right)
{
// 如果右子树存在,就找右子树的最左节点
node* cur = _node->_right;
while (cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else
{
// 右子树不存在,找 左孩子的祖先
node* cur = _node;
node* parent = cur->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
private:
node* _node;
};
template<class K, class T, class KOfT, class Compare>
class RBTree
{
using node = RBTreeNode<T>;
public:
using iterator = _RBTree_Itreator<T>;
iterator begin()
{
node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);
}
// 右单旋
void RotateR(node* cur)
{
node* parent = cur->_parent;
node* subL = cur->_left;
node* subR = cur->_right;
node* subLR = subL->_right;
subL->_right = cur;
cur->_left = subLR;
if(subLR)
subLR->_parent = cur;
cur->_parent = subL;
subL->_parent = parent;
// 若 cur 为根节点,就要更新根节点
if (cur == _root)
{
_root = subL;
}
else
{
if (parent->_left == cur)
parent->_left = subL;
else
parent->_right = subL;
}
}
// 左单旋
void RotateL(node* cur)
{
node* parent = cur->_parent;
node* subL = cur->_left;
node* subR = cur->_right;
node* subRL = subR->_left;
subR->_left = cur;
cur->_right = subRL;
if(subRL)
subRL->_parent = cur;
cur->_parent = subR;
subR->_parent = parent;
// 若 cur 为根节点,就要更新根节点
if (cur == _root)
{
_root = subR;
}
else
{
if (parent->_left == cur)
parent->_left = subR;
else
parent->_right = subR;
}
}
bool Insert(const T& val)
{
// 如果 root 为空,直接 new 然后返回即可
if (_root == nullptr)
{
_root = new node(val);
_root->_col = BLACK;
return true;
}
KOfT kot;
Compare comp;
// 找新节点该插入的位置
node* cur = _root;
node* parent = _root;
while (cur)
{
if (!comp(kot(val), kot(cur->_val)))
{
// 新节点的值比当前节点的大,向右找
parent = cur;
cur = cur->_right;
}
else if (comp(kot(val), kot(cur->_val)))
{
// 新节点的值比当前节点的小,向左找
parent = cur;
cur = cur->_left;
}
else
{
// 有相等的值,插入失败
return false;
}
}
cur = new node(val);
if (comp(kot(val), kot(parent->_val)))
{
// 新节点的值比父节点小,在左边
parent->_left = cur;
cur->_parent = parent;
}
else
{
// 新节点的值比父节点大,在右边
parent->_right = cur;
cur->_parent = parent;
}
// 改颜色
while (parent && parent->_col == RED)
{
node* grandparent = parent->_parent;
node* uncle = grandparent->_right;
if (grandparent->_right == parent)
uncle = grandparent->_left;
if (uncle && uncle->_col == RED)
{
// 叔叔存在且为红
grandparent->_col = RED;
parent->_col = BLACK;
uncle->_col = BLACK;
cur = grandparent;
parent = cur->_parent;
}
else
{
// 叔叔不存在 或 为黑
// parent 在 grandparent 左边
if (grandparent->_left == parent)
{
// cur 和 parent 都在左边,右单旋
// g
// p u
// c
if (parent->_left == cur)
{
RotateR(grandparent);
parent->_col = BLACK;
grandparent->_col = RED;
}
else
{
// parent 在左,cur 在右
// g
// p u
// c
// 先左单旋,再右单旋
RotateL(parent);
RotateR(grandparent);
grandparent->_col = RED;
cur->_col = BLACK;
}
}
else
{
// parent 在右边
if (parent->_right == cur)
{
// cur 和 parent 都在右边,左单旋
// g
// u p
// c
RotateL(grandparent);
parent->_col = BLACK;
grandparent->_col = RED;
}
else
{
// parent 在右,cur 在左
// g
// u p
// c
// 先右单旋,再左单旋
RotateR(parent);
RotateL(grandparent);
grandparent->_col = RED;
cur->_col = BLACK;
}
}
break;
}
}
_root->_col = BLACK;
return true;
}
// 查看是否出现连续的红色节点
bool CheckRedNodes(node* cur)
{
KOfT kot;
if (cur == nullptr)
return true;
if (cur->_col == RED && cur->_parent->_col == RED)
{
cout << kot(cur->_val) << " 出现连续的红色节点\n";
return false;
}
return CheckRedNodes(cur->_left) && CheckRedNodes(cur->_right);
}
// 查看每条路径上的黑色节点个数
bool CheckPath(node* cur, int BNum, int& pivot)
{
if (cur == nullptr)
return true;
if (cur->_col == BLACK) BNum++;
if (cur->_left == nullptr && cur->_right == nullptr)
{
if (pivot == 0)
{
pivot = BNum;
cout << "每条路径黑色节点个数: " << BNum << endl;
return true;
}
else
{
if (BNum != pivot)
{
cout << cur->_val.first << "黑色节点个数不符合\n";
}
return BNum == pivot;
}
}
return CheckPath(cur->_left, BNum, pivot)
&& CheckPath(cur->_right, BNum, pivot);
}
// 检查红黑树是否正确
bool IsBalance()
{
if (_root && _root->_col == RED)
{
cout << " 根节点为红色,错误\n";
return false;
}
int pivot = 0;
return CheckRedNodes(_root)
&& CheckPath(_root, 0, pivot);
}
private:
node* _root = nullptr;
};六、封装 map 和 set
1、封装 map
对于 map,格式是 map<K, V, Compare>,而在红黑树中的节点中存的值是 pair<K, V>
我们要写一个仿函数 KOfTMap 让红黑树拿到 key,也就是拿到 pair<K, V> 中的 K,直接返回pair.first 即可。
因此,map 对应的红黑树传入模版为:
RBTree<K, std::pair<K, V>, KOfTMap<K, V>, Compare> _tree;
具体实现
cpp
// 通过 T 也就是 pair 拿到 K
// 红黑树的插入的关键值是 K
template<class K, class V>
struct KOfTMap
{
const K& operator()(const std::pair<K, V>& val)
{
return val.first;
}
};
template<class K, class V, class Compare = std::less<K>>
class Map
{
public:
// 不知道是类型还是静态成员变量,加上 typename 表示是类型
using iterator = typename RBTree<K, std::pair<K, V>, KOfTMap<K, V>, Compare>::iterator;
public:
// 插入
bool insert(const std::pair<K, V>& val)
{
return _tree.Insert(val);
}
// 检查
bool Check()
{
return _tree.IsBalance();
}
// 迭代器的 begin 与 end
iterator begin()
{
return _tree.begin();
}
iterator end()
{
return _tree.end();
}
private:
RBTree<K, std::pair<K, V>, KOfTMap<K, V>, Compare> _tree; // 上面实现的红黑树
};2、封装 set
对于 set,格式是 set<K, Compare>,而在红黑树中的节点中存的值是 K
我们要写一个仿函数 KOfTSet 让红黑树拿到 key,直接返回K 即可。
因此,set对应的红黑树传入模版为:
RBTree<K, K, KOfTSet<K>, Compare> _tree;
具体代码实现:
cpp
template<class K>
struct KOfTSet
{
// 拿到 K
const K& operator()(const K& val)
{
return val;
}
};
template<class K, class Compare = std::less<K>>
class Set
{
public:
// 不知道是类型还是静态成员变量,加上 typename 表示是类型
using iterator = typename RBTree<K, K, KOfTSet<K>, Compare>::iterator;
public:
// 插入
bool insert(const K& val)
{
return _tree.Insert(val);
}
// 检查
bool Check()
{
return _tree.IsBalance();
}
// 迭代器 begin 与 end
iterator begin()
{
return _tree.begin();
}
iterator end()
{
return _tree.end();
}
private:
RBTree<K, K, KOfTSet<K>, Compare> _tree; // 上面实现的红黑树
};感谢大家观看♪(・ω・)ノ