【机器学习】实战：天池工业蒸汽量项目（三）模型预测

道友老李2025-01-16 8:36

文章目录

个人主页： 道友老李
欢迎加入社区： 道友老李的学习社区

【机器学习】实战：天池工业蒸汽量项目（二）特征工程

项目介绍

在工业环境中，蒸汽是一种非常常见的能源形式，被广泛应用于各种加热过程、发电以及其它工艺过程中。准确地预测蒸汽的需求量可以帮助企业优化其生产计划，提高能效，减少能源浪费，并降低运营成本。

通常，这样的项目会包含以下几个方面：

  • 数据收集：从工业现场的传感器和其他数据源收集历史数据，包括但不限于温度、压力、流量等与蒸汽生成和消耗相关的参数。
  • 数据分析：对收集到的数据进行清洗、预处理，并通过统计分析或可视化工具来理解数据的特性。
  • 模型建立：使用机器学习算法或者深度学习技术构建预测模型，这些模型能够基于输入的历史数据预测未来的蒸汽需求量。常用的模型可能包括线性回归、随机森林、支持向量机（SVM）、神经网络等。
  • 模型评估：通过交叉验证或其他评估方法测试模型的性能，确保模型具有良好的泛化能力，能够在未见过的数据上做出准确的预测。
  • 解决方案部署：将训练好的模型部署到实际的工业环境中，实时接收新数据并输出预测结果，帮助工厂实现更高效的能源管理。
  • 持续优化：根据模型在真实环境中的表现不断调整和优化，以适应变化的工作条件和技术进步。

火力发电的基本原理是：燃料在燃烧时加热水生成蒸汽，蒸汽压力推动汽轮机旋转，然后汽轮机带动发电机旋转，产生电能。在这一系列的能量转化中，影响发电效率的核心是锅炉的燃烧效率，即燃料燃烧加热水产生高温高压蒸汽。锅炉的燃烧效率的影响因素很多，包括锅炉的可调参数，如燃烧给量，一二次风，引风，返料风，给水水量；以及锅炉的工况，比如锅炉床温、床压，炉膛温度、压力，过热器的温度等。

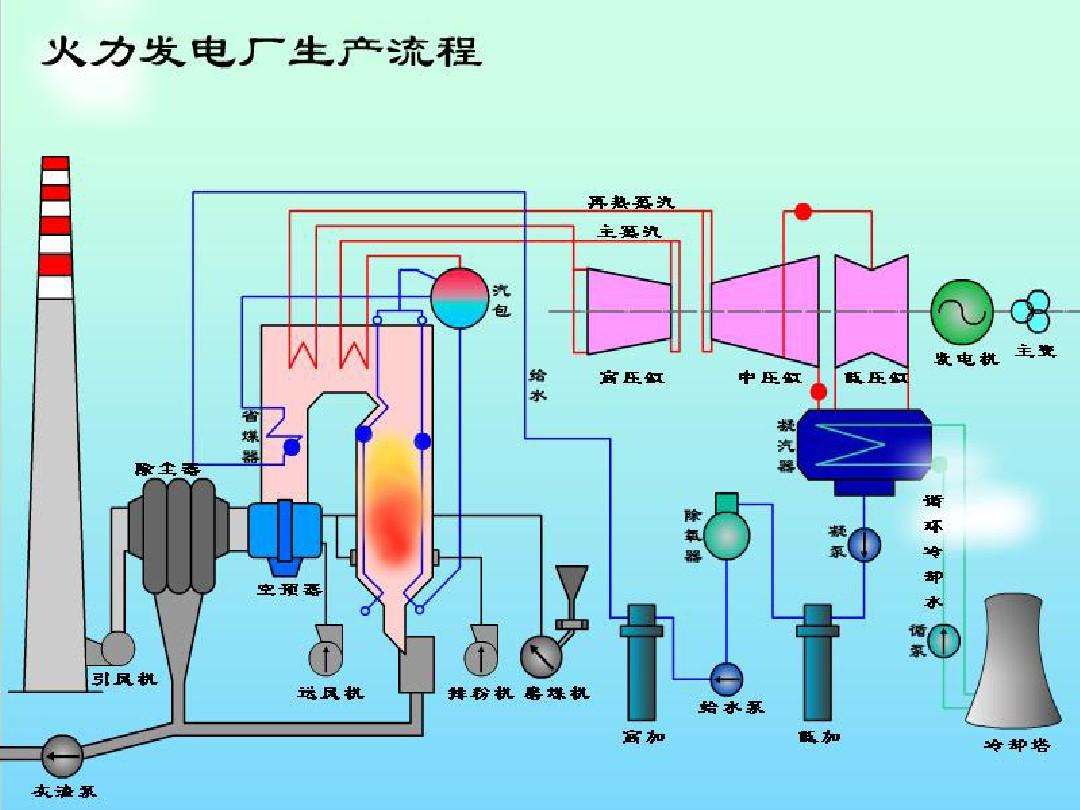
经脱敏后的锅炉传感器采集的数据（采集频率是分钟级别），根据锅炉的工况，预测产生的蒸汽量。

1、导入相应算法

python 复制代码 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression  #线性回归
from sklearn.ensemble import RandomForestRegressor #随机森林回归
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.svm import SVR  #支持向量回归
import lightgbm as lgb #lightGbm模型
from xgboost import XGBRFRegressor

from sklearn.model_selection import train_test_split # 切分数据
from sklearn.metrics import mean_squared_error #评价指标

from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
import warnings
warnings.filterwarnings('ignore')

2、加载数据

2.1、未降维数据

python 复制代码 
all_data = pd.read_csv('./processed_zhengqi_data2.csv')

# 训练数据
cond = all_data['label'] == 'train'
train_data = all_data[cond]
train_data.drop(labels = 'label',axis = 1,inplace = True)
# 切分数据 训练数据80% 验证数据20%
X_train,X_valid,y_train,y_valid=train_test_split(train_data.drop(labels='target',axis = 1),
                                                 train_data['target'],
                                                 test_size=0.2)
# 测试数据
cond2 = all_data['label'] == 'test'
test_data = all_data[cond2]
test_data.drop(labels = ['label','target'],axis = 1,inplace = True)

2.2、降维数据

python 复制代码 
#采用 pca 保留特征的数据
train_data_pca = np.load('./train_data_pca.npz')['X_train']
target_data_pca = np.load('./train_data_pca.npz')['y_train']

# 切分数据 训练数据80% 验证数据20%
X_train_pca,X_valid_pca,y_train_pca,y_valid_pca=train_test_split(train_data_pca,target_data_pca,
                                                               test_size=0.2)
test_data_pca = np.load('./test_data_pca.npz')['X_test']

3、定义绘制模型学习曲线函数

python 复制代码 
def plot_learning_curve(model,title,X,y,cv=None):
  
    # 学习曲线计算
    train_sizes, train_scores, test_scores = learning_curve(model, X, y, cv=cv)
  
    # 训练数据得分和测试数据得分平均值与方差计算
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
  
  
    # 训练数据得分可视化
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
             label="Training score")
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                     train_scores_mean + train_scores_std, alpha=0.1,color="r")
    # 测试数据得分可视化
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
             label="Cross-validation score")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
                     test_scores_mean + test_scores_std, alpha=0.1, color="g")
    # 画图设置
    plt.grid() # 网格线设置
    plt.legend(loc="best") # 图例设置
    # 标题标签设置
    plt.title(title)
    plt.xlabel("Training examples")
    plt.ylabel("Score")

4、多元线性回归建模预测

4.1、模型训练

降维数据建模验证

python 复制代码 
clf = LinearRegression()
clf.fit(X_train_pca, y_train_pca)
score = mean_squared_error(y_valid_pca, clf.predict(X_valid_pca))
print("LinearRegression:   ", score)

未降维数据建模验证

python 复制代码 
clf = LinearRegression()
clf.fit(X_train, y_train)
score = mean_squared_error(y_valid, clf.predict(X_valid))
print("LinearRegression:   ", score)

4.2、绘制学习曲线

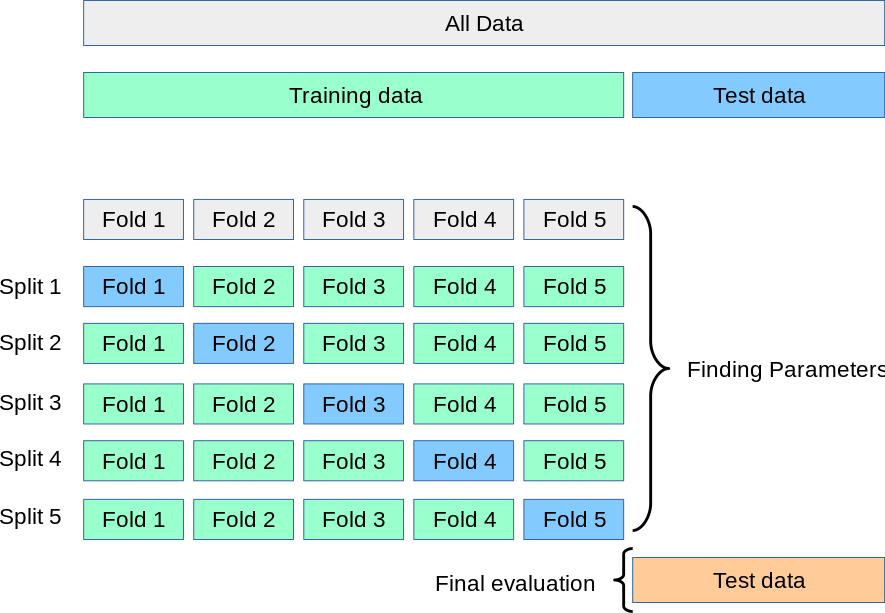
学习曲线是不同训练集大小，模型在训练集和验证集上的得分变化曲线。也就是以样本数为横坐标，训练和交叉验证集上的得分（如准确率）为纵坐标。

learning curve可以帮助我们判断模型现在所处的状态：

  • 过拟合（overfiting / high variance 高方差） 说明模型能够很好的拟合已知数据，但是泛化能力很差，属于高方差
  • 欠拟合（underfitting / high bias 高偏差）这说明模拟对已知数据和未知都不能进行准确的预测，属于高偏差

降维数据学习曲线

python 复制代码 
X = X_train_pca
y = y_train_pca
# 多元线性回归模型学习曲线图
title = "LinearRegression"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
estimator = LinearRegression()    #建模
plot_learning_curve(estimator, title, X, y, cv = cv)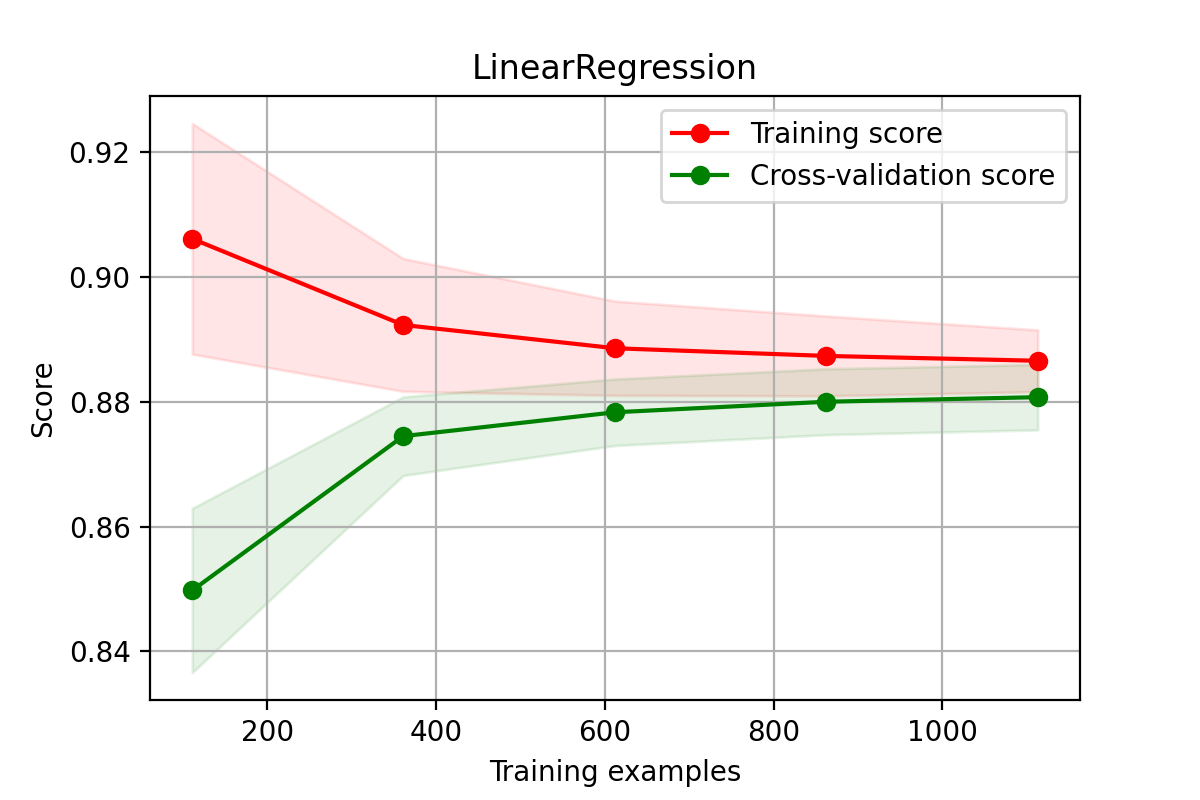

非降维数据学习曲线

python 复制代码 
X = X_train
y = y_train
# 多元线性回归模型学习曲线图
title = "LinearRegression"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
estimator = LinearRegression()    #建模
plot_learning_curve(estimator, title, X, y, cv = cv)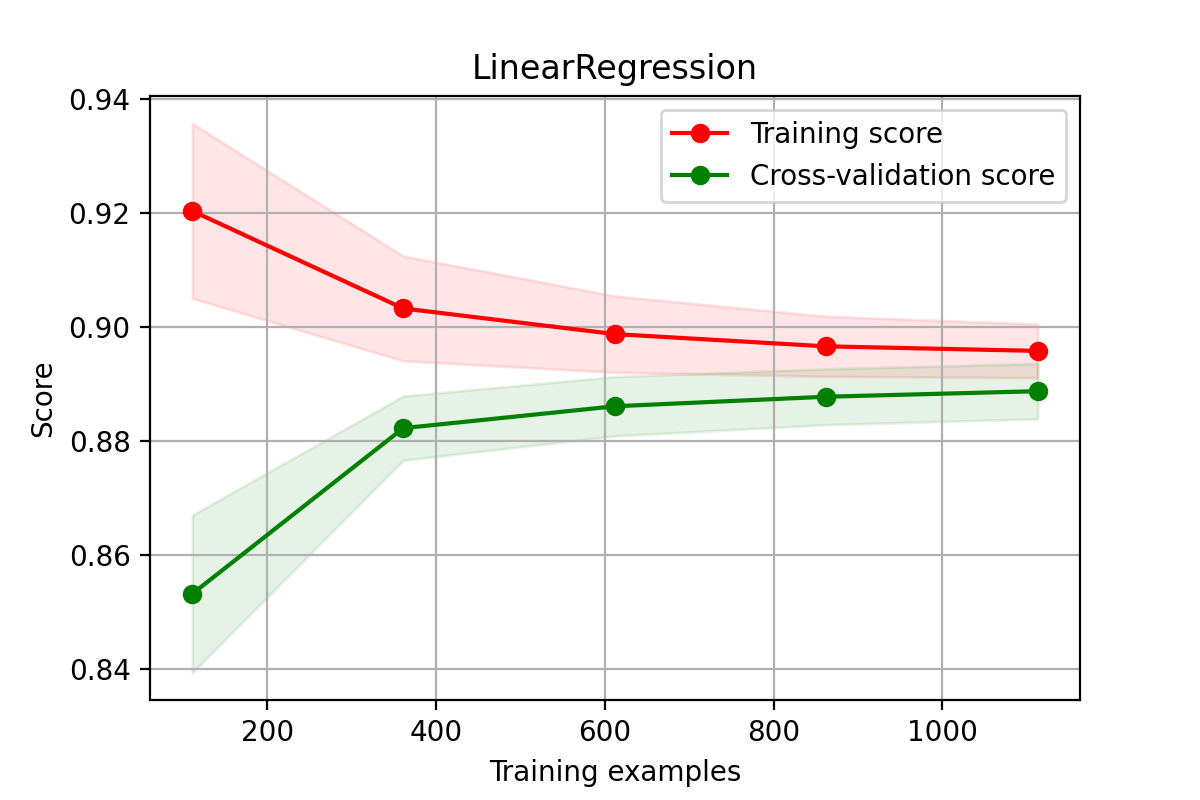

4.3、模型预测

降维数据建模预测提交

python 复制代码 
# 得分是：0.1598
model = LinearRegression()
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./多元线性回归模型预测(降维数据).txt',y_)

非降维数据建模预测提交

python 复制代码 
# 得分是：0.1620
model = LinearRegression()
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./多元线性回归模型预测(非降维数据).txt',y_)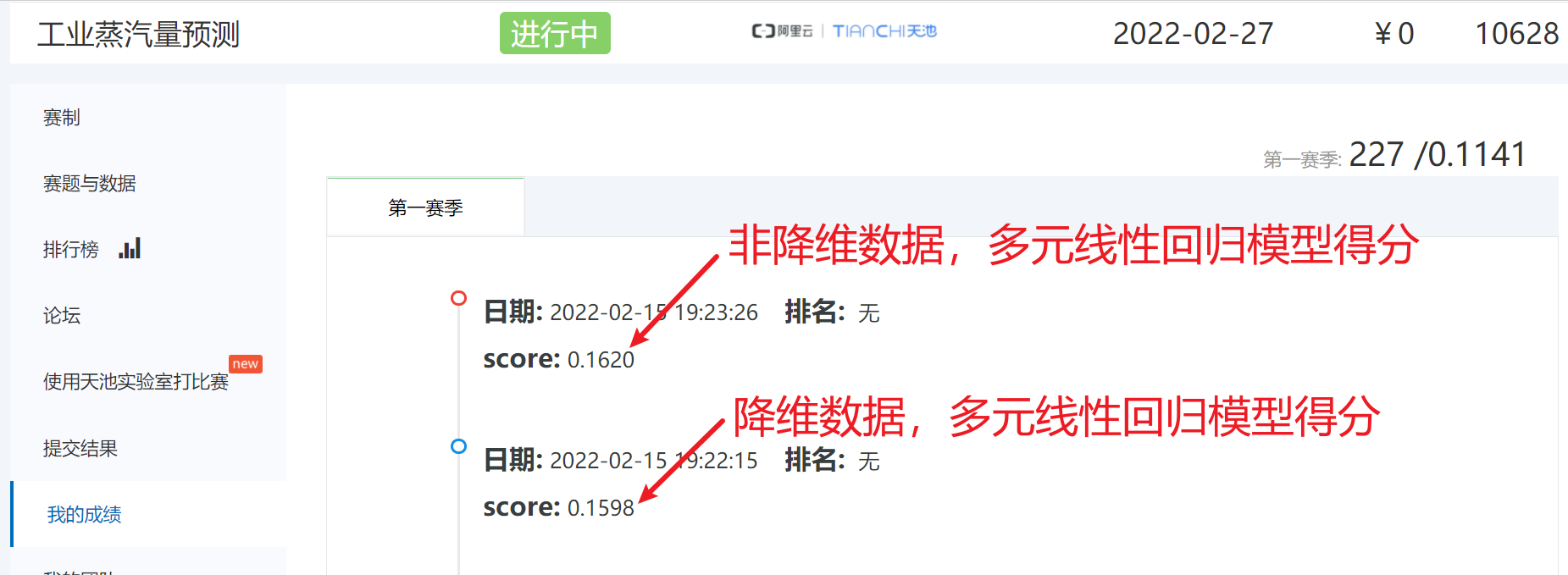

5、随机森林建模预测

5.1、模型训练

降维数据建模验证

python 复制代码 
model = RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
model.fit(X_train_pca, y_train_pca)
score = mean_squared_error(y_valid_pca, model.predict(X_valid_pca))
print("随机森林:   ", score)

非降维数据建模验证

python 复制代码 
model = RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
model.fit(X_train, y_train)
score = mean_squared_error(y_valid, model.predict(X_valid))
print("LinearRegression:   ", score)

5.2、绘制学习曲线

绘制学习曲线比较耗时间，这里绘制非降维数据的学习曲线

python 复制代码 
%%time
# 比较耗时：5min 14s
X = X_train
y = y_train
# 随机森林模型学习曲线图
title = "RandomForestRegressor"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./12-随机森林非降维数据学习曲线.png',dpi = 200)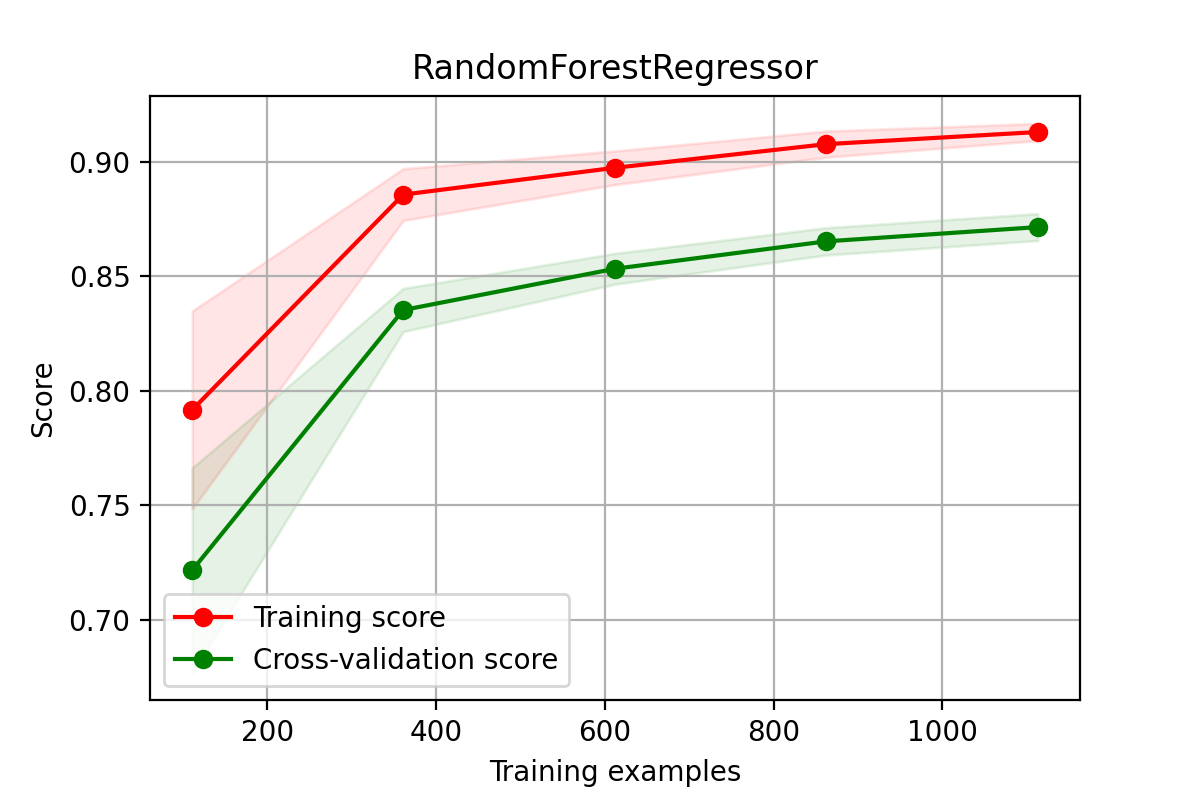

5.3、模型预测

降维数据建模预测提交

python 复制代码 
# 得分是：1.0579
model =  RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./随机森林模型预测(降维数据).txt',y_)

非降维数据建模预测提交

python 复制代码 
# 得分是：0.1461
model = RandomForestRegressor(n_estimators=200, # 200棵树模型
                            max_depth= 10,
                            max_features = 'auto',# 构建树时，特征筛选量
                            min_samples_leaf=10,# 是叶节点所需的最小样本数
                            min_samples_split=40,# 是分割所需的最小样本数
                            criterion='squared_error')
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./随机森林模型预测(非降维数据).txt',y_)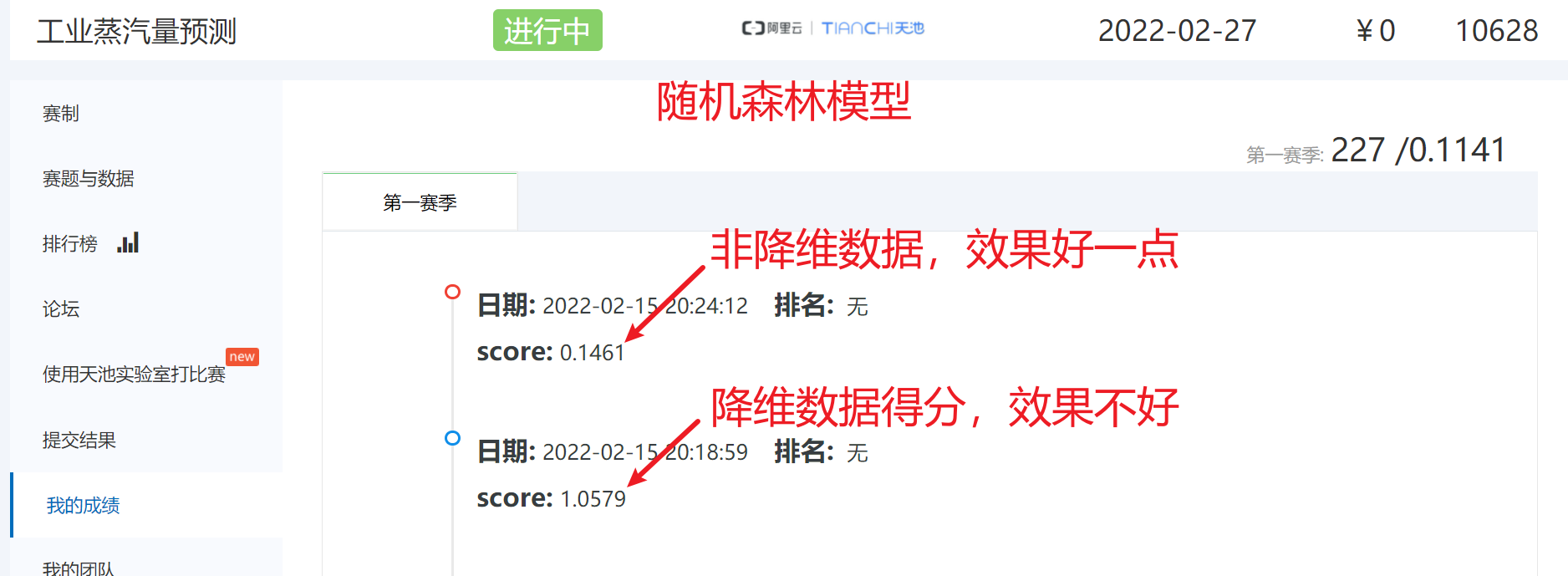

6、SVR支持向量机

6.1、模型训练

降维数据

python 复制代码 
model = SVR(kernel='rbf',C = 1,gamma=0.01,tol = 0.0001,epsilon=0.3)
model.fit(X_train_pca, y_train_pca)
score = mean_squared_error(y_valid_pca, model.predict(X_valid_pca))
print("SVR得分:   ", score)

非降维数据

python 复制代码 
model = SVR(kernel='rbf')
model.fit(X_train, y_train)
score = mean_squared_error(y_valid, model.predict(X_valid))
print("SVR得分:   ", score)

6.2、绘制学习曲线

降维数据

python 复制代码 
%%time
X = X_train_pca
y = y_train_pca
# 随机森林模型学习曲线图
title = "RandomForestRegressor"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = SVR(kernel='rbf',C = 1,gamma=0.01,tol = 0.0001,epsilon=0.3)
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./15-SVR降维数据学习曲线.png',dpi = 200)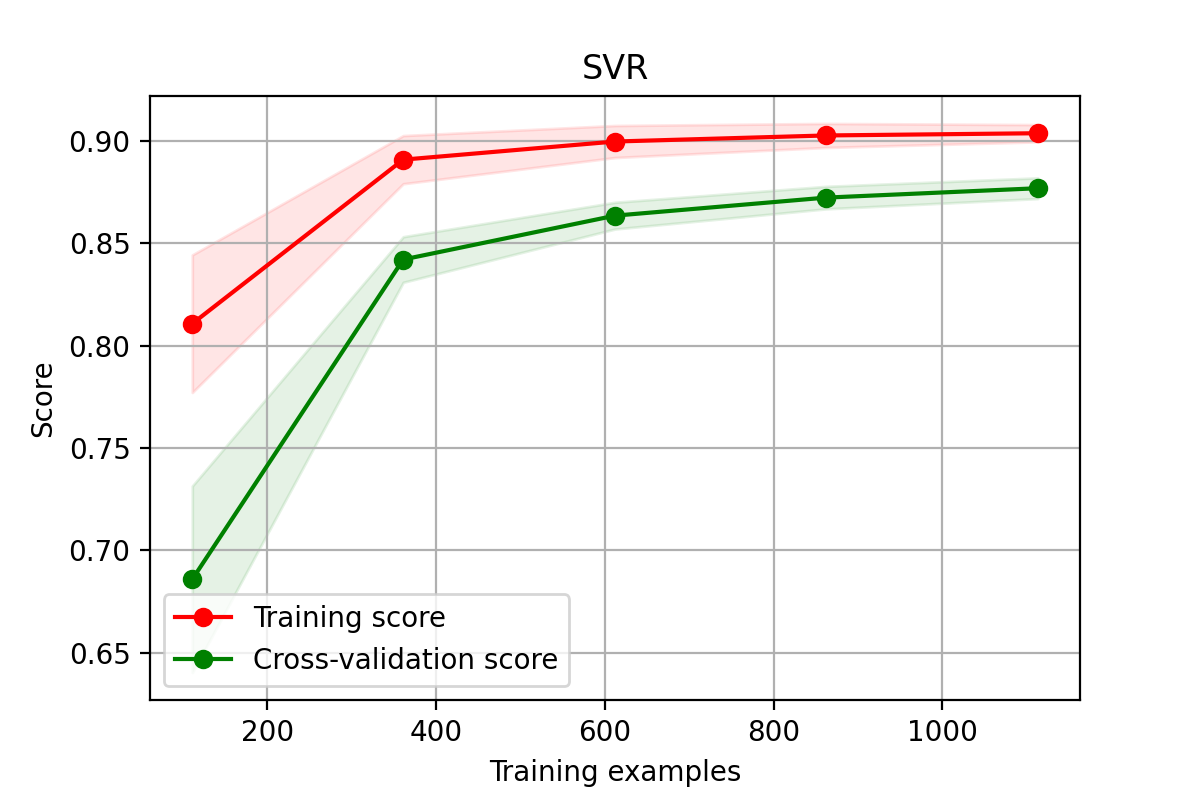

非降维数据

python 复制代码 
%%time
X = X_train
y = y_train
# 随机森林模型学习曲线图
title = "RandomForestRegressor"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = SVR(kernel='rbf')
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./16-SVR非降维数据学习曲线.png',dpi = 200)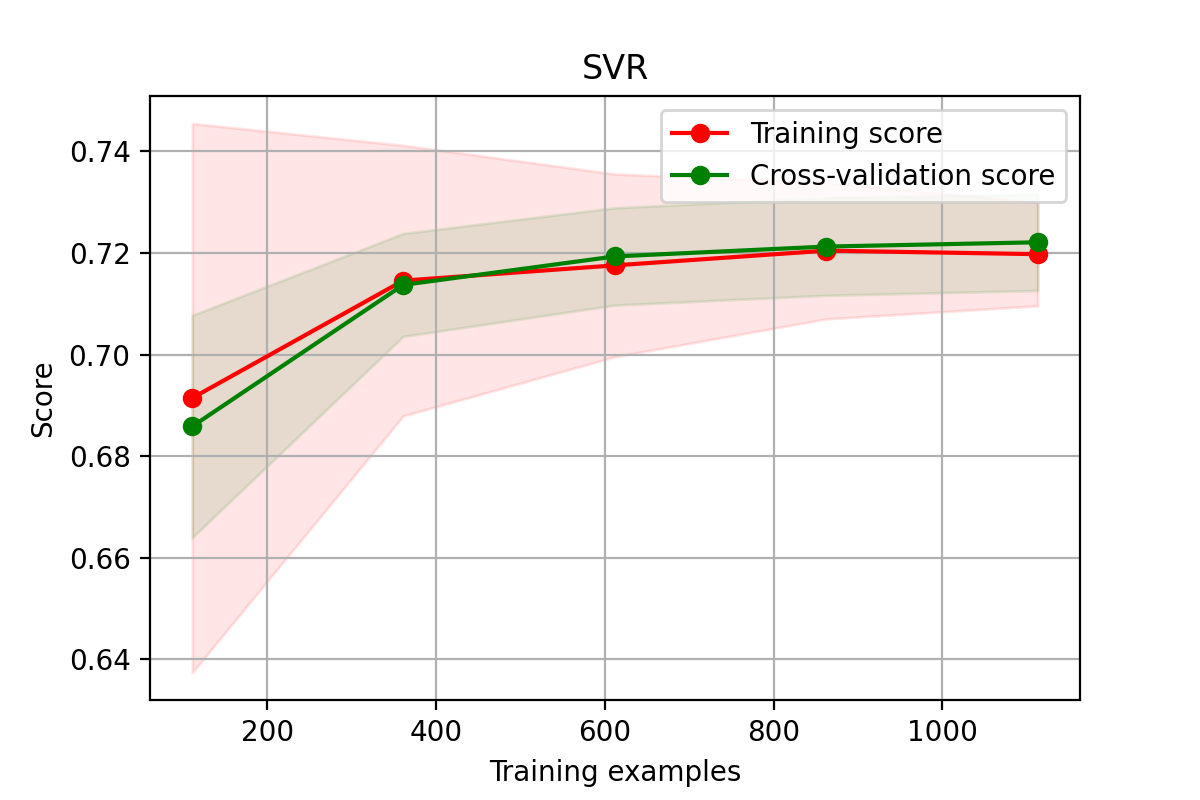

6.3、模型预测

降维数据

python 复制代码 
# 得分是：0.2654
model =  SVR(kernel='rbf',C = 1,gamma=0.01,tol = 0.0001,epsilon=0.3)
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./SVR模型预测(降维数据).txt',y_)

非降维数据

python 复制代码 
# 得分是：1.9934
model =SVR(kernel='rbf')
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./SVR模型预测(非降维数据).txt',y_)

poly多项式核函数建模预测--降维数据

python 复制代码 
# 得分是：4.7068
model =  SVR(kernel='poly')
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./SVR-poly模型预测(降维数据).txt',y_)

poly多项式核函数建模预测--非降维数据

python 复制代码 
# 得分是：0.7423
model =SVR(kernel='poly')
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./SVR--poly模型预测(非降维数据).txt',y_)

7、GBDT梯度提升树

7.1、模型训练

降维数据

python 复制代码 
model = GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
model.fit(X_train_pca, y_train_pca)
score = mean_squared_error(y_valid_pca, model.predict(X_valid_pca))
print("GBDT得分:   ", score)

非降维数据

python 复制代码 
model = GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
model.fit(X_train, y_train)
score = mean_squared_error(y_valid, model.predict(X_valid))
print("GBDT得分:   ", score)

7.2、绘制学习曲线

降维数据学习曲线

python 复制代码 
%%time
X = X_train_pca
y = y_train_pca
# 随机森林模型学习曲线图
title = "GBDT"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = SVR(kernel='rbf',C = 1,gamma=0.01,tol = 0.0001,epsilon=0.3)
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./17-GBDT降维数据学习曲线.png',dpi = 200)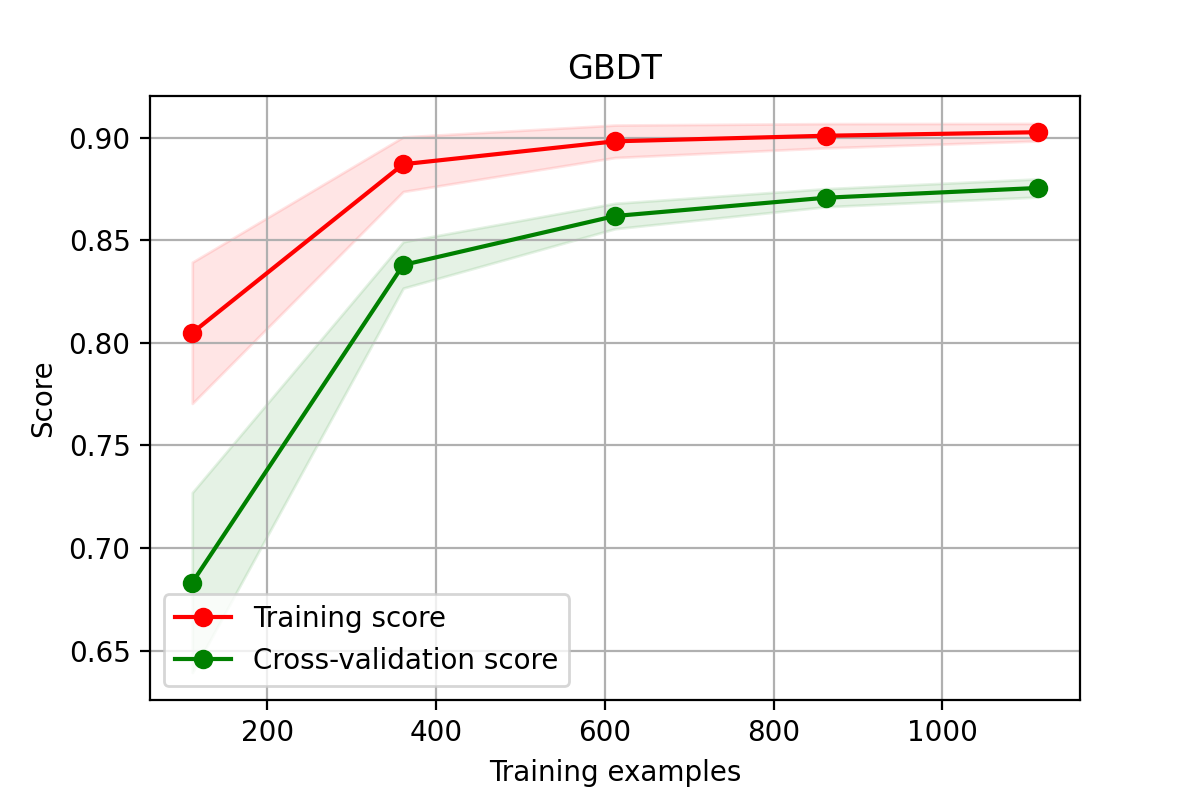

7.3、模型预测

降维数据

python 复制代码 
# 得分是：0.3765
model =  GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./GBDT模型预测(降维数据).txt',y_)

非降维数据

python 复制代码 
# 得分是：0.1392
model = GradientBoostingRegressor(learning_rate=0.03, # 学习率
                                loss='huber',  # 损失函数
                                max_depth=14, # 决策树深度
                                max_features='sqrt',# 节点分裂时参与判断的最大特征数
                                min_samples_leaf=10,# 是叶节点所需的最小样本数
                                min_samples_split=40,# 是分割所需的最小样本数
                                n_estimators=300,# 集成树数量
                                subsample=0.8)# 抽样比例
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./GBDT模型预测(非降维数据).txt',y_)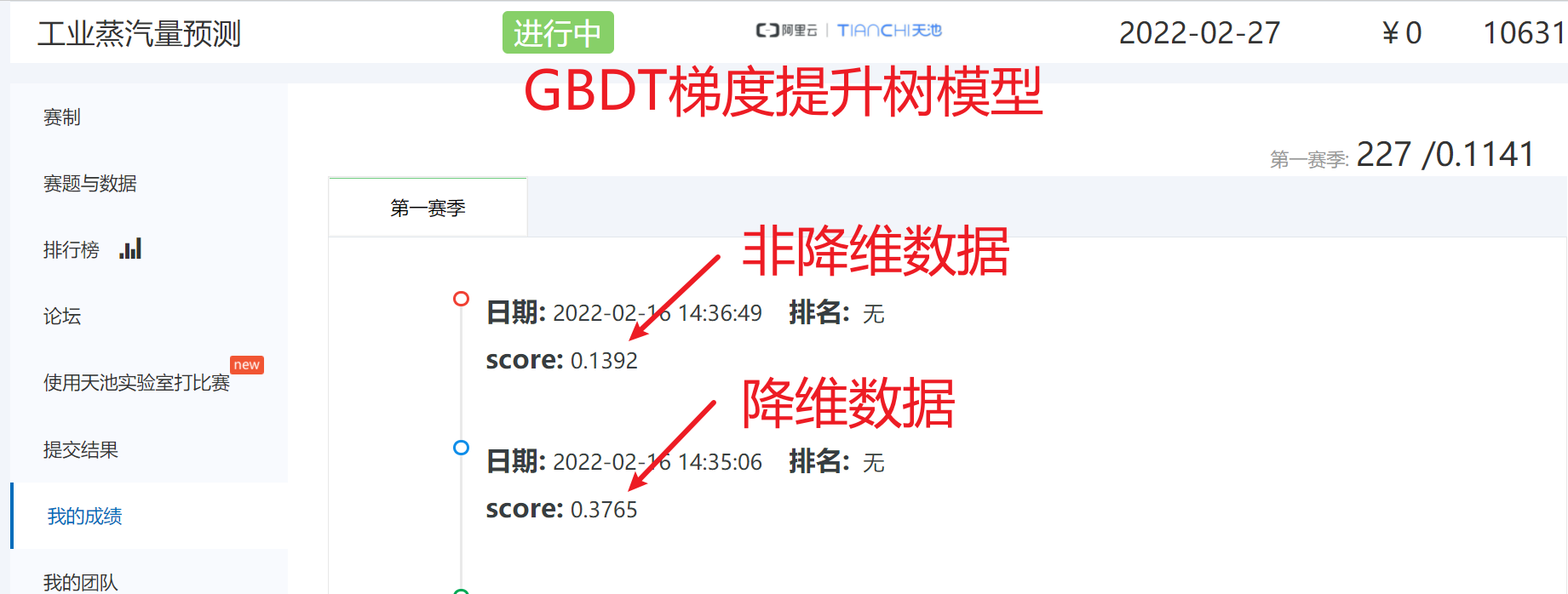

8、lightGBM

8.1、模型训练

降维数据

python 复制代码 
model = lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=300,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
model.fit(X_train_pca, y_train_pca)
score = mean_squared_error(y_valid_pca, model.predict(X_valid_pca))
print("LGB得分:   ", score)

非降维数据

python 复制代码 
model = lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=300,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
model.fit(X_train, y_train)
score = mean_squared_error(y_valid, model.predict(X_valid))
print("LGB得分:   ", score)

8.2、绘制学习曲线

降维数据

python 复制代码 
%%time
X = X_train
y = y_train
# lightGBM模型学习曲线图
title = "lightGBM"
cv = ShuffleSplit(n_splits=100, test_size=0.5)
model = lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=300,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
plot_learning_curve(model, title, X, y, cv = cv)
plt.savefig('./22-lightGBM非降维数据学习曲线.png',dpi = 200)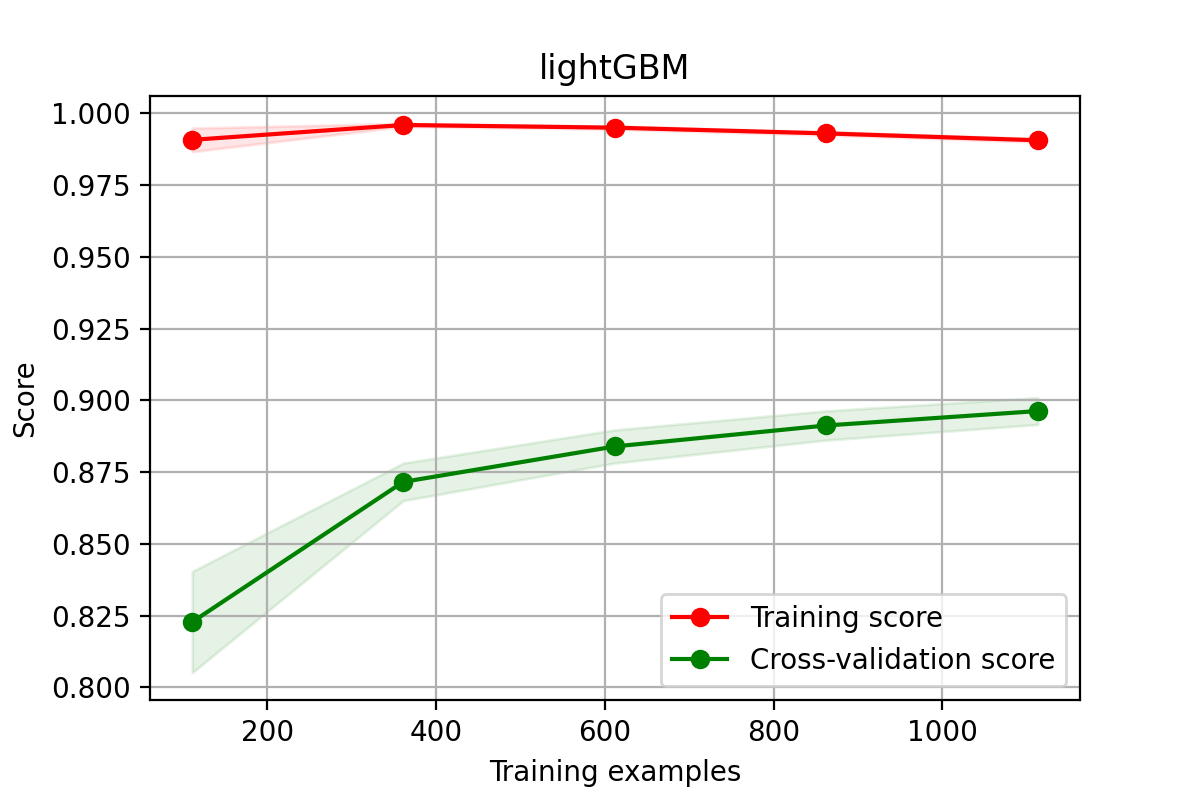

8.3、模型预测

降维数据

python 复制代码 
# 得分是：0.6383
model =  lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=100,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./lightGBM模型预测(降维数据).txt',y_)

非降维数据

python 复制代码 
# 得分是：0.1378
model = lgb.LGBMRegressor(learning_rate=0.05, # 学习率
                        n_estimators=100,# 集成树数量
                        min_child_samples=10,# 是叶节点所需的最小样本数
                        max_depth=5, # 决策树深度
                        num_leaves = 25,
                        colsample_bytree =0.8,#构建树时特征选择比例
                        subsample=0.8,# 抽样比例
                        reg_alpha = 0.5,
                        reg_lambda = 0.1 )
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./lightGBM模型预测(非降维数据).txt',y_)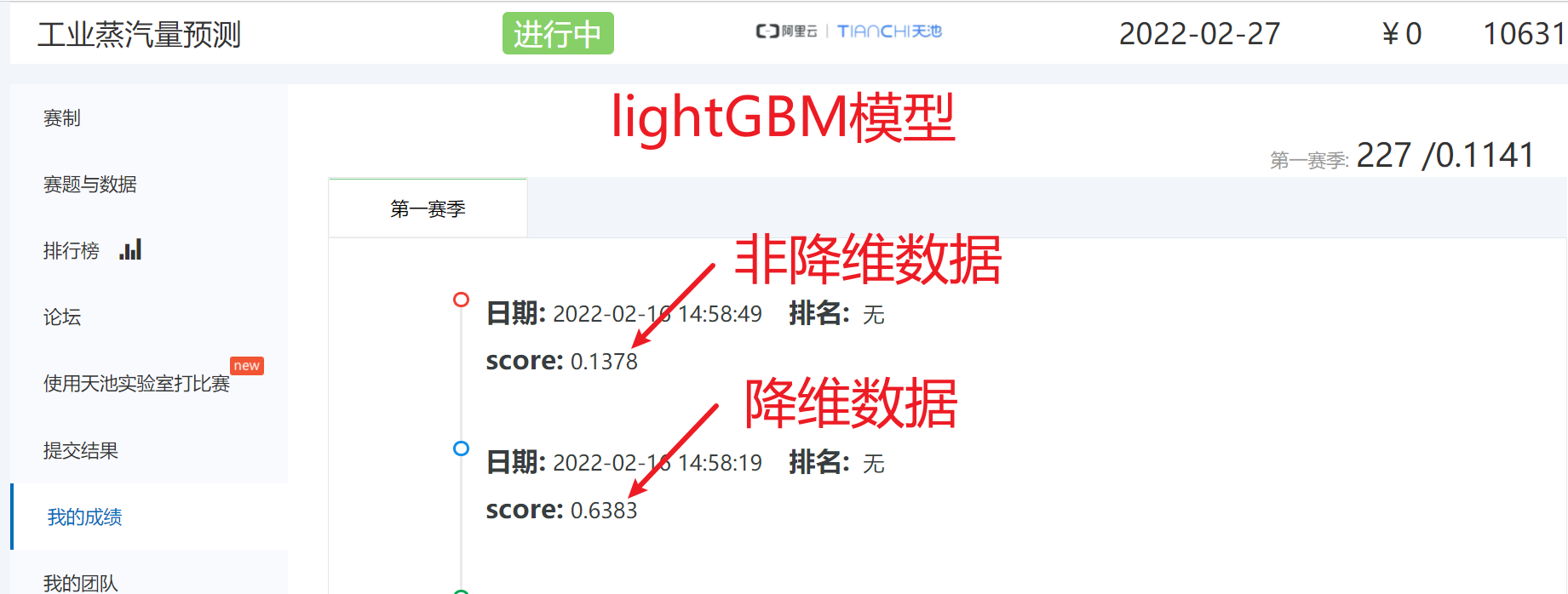

9、Xgboost

9.1、模型训练

降维数据

python 复制代码 
model = XGBRFRegressor(n_estimators = 300, 
                       max_depth=15,
                       subsample = 0.8,
                       colsample_bytree = 0.8,
                       learning_rate =1,
                       gamma = 0,
                       reg_lambda= 0 ,# L2正则化
                       reg_alpha = 0,verbosity=1)# L1正则化
model.fit(X_train_pca, y_train_pca)
score = mean_squared_error(y_valid_pca, model.predict(X_valid_pca))
print("Xgboost得分:   ", score)

非降维数据

python 复制代码 
model = XGBRFRegressor(n_estimators = 300, 
                       max_depth=15,
                       subsample = 0.8,
                       colsample_bytree = 0.8,
                       learning_rate =1,
                       gamma = 0,
                       reg_lambda= 0 ,# L2正则化
                       reg_alpha = 0,verbosity=1)# L1正则化
model.fit(X_train, y_train)
score = mean_squared_error(y_valid, model.predict(X_valid))
print("Xgboost得分:   ", score)

9.2、模型预测

降维数据

python 复制代码 
# 得分是：0.6798
model = XGBRFRegressor(n_estimators = 300, 
                       max_depth=15,
                       subsample = 0.8,
                       colsample_bytree = 0.8,
                       learning_rate =1,
                       gamma = 0,
                       reg_lambda= 0 ,# L2正则化
                       reg_alpha = 0,verbosity=1)# L1正则化
model.fit(train_data_pca,target_data_pca)
y_ = model.predict(test_data_pca)
display(y_)
np.savetxt('./Xgboost模型预测(降维数据).txt',y_)

非降维数据

python 复制代码 
# 得分是：0.1329
model = XGBRFRegressor(n_estimators = 300, 
                       max_depth=15,
                       subsample = 0.8,
                       colsample_bytree = 0.8,
                       learning_rate =1,
                       gamma = 0,
                       reg_lambda= 0 ,# L2正则化
                       reg_alpha = 0,verbosity=1)# L1正则化
model.fit(train_data.drop('target',axis = 1),train_data['target'])
y_ = model.predict(test_data)
display(y_)
np.savetxt('./Xgboost模型预测(非降维数据).txt',y_)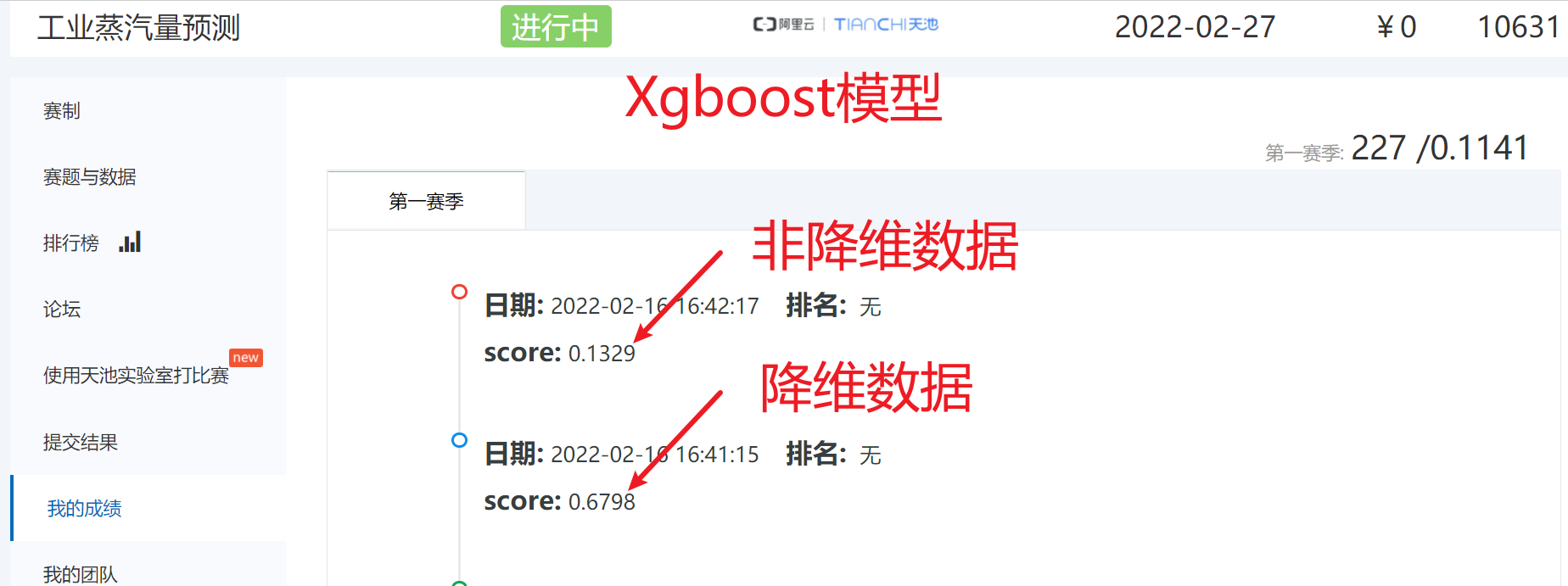

10、结论

  • 集成算法对非降维数据，表现更好
  • 多元线性回归、SVR对降维数据，表现更好
  • 整体来说，集成算法效果更好
  • 随机森林：0.1461
  • GBDT：0.1392
  • lightGBM：0.1378
  • Xgboost：0.1329

还需要，继续对特征进行挖掘、对算法进行融合！

相关推荐
阿里云大数据AI技术7 分钟前
面向法律场景的大模型RAG检索增强解决方案
人工智能·阿里云·llm·rag·pai
程序猿阿伟14 分钟前
《鸿蒙Next微内核：解锁人工智能决策树并行计算的加速密码》
人工智能·决策树·harmonyos
西岸风16616 分钟前
【全套】基于分类算法的学业警示预测信息管理系统
人工智能·分类·数据挖掘
远洋录26 分钟前
Vue 开发者的 React 实战指南：表单处理篇
前端·人工智能·react
亲持红叶29 分钟前
Chapter5.3 Decoding strategies to control randomness
人工智能·python·gpt·深度学习·算法·机器学习
大模型之路30 分钟前
微软震撼发布：Phi-4语言模型登陆Hugging Face
人工智能·microsoft·语言模型·大模型·llm·phi-4
蚝油菜花1 小时前
FlowiseAI：Star！集成多种模型和100+组件的 LLM 应用低代码开发平台，拖拽组件轻松构建程序
人工智能·开源
CM莫问1 小时前
python实战（十四）——Bert-BiLSTM-CRF命名实体识别
人工智能·python·深度学习·算法·bert·实体识别·crf
ZZZXXE1 小时前
GLM: General Language Model Pretraining with Autoregressive Blank Infilling论文解读
人工智能·语言模型·自然语言处理
martian6652 小时前
深入详解人工智能语音识别之声学模型与语言模型：掌握HMM、CTC等方法
人工智能·语言模型·语音识别·声学模型
热门推荐
01玄机平台应急响应—webshell查杀02Dell服务器升级ubuntu 22.04失败解决03半导体应用系统一些小知识收集(strip&wafer mapping,EAP&scada)04[Docker]使用Docker部署常见的中间件05密码学原理技术-第六章-introduction to pulibc-key cryptography06优化手机性能，解决卡顿问题：关闭这3个微信开关，释放内存空间07年出货2亿台，只赚“辛苦钱”！又一家代工巨头押宝汽车电子08go下载依赖提示连接失败09渗透测试之SQLMAP工具详解 kali自带SQLmap解释 重点sqlmap --tamper 使用方式详解 搞完你就很nice了10ChatGPT + Stable Diffusion + 百度AI + MoviePy 实现文字生成视频，小说转视频，自媒体神器！(二)