解析解推导
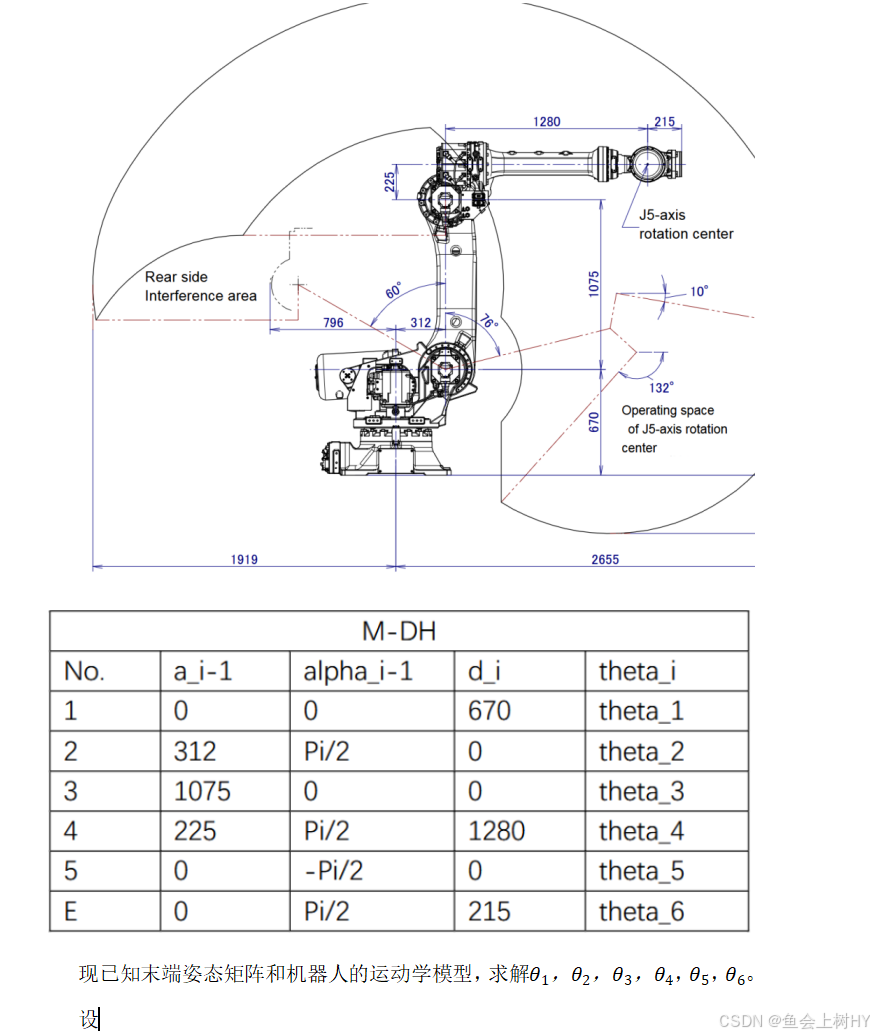
假设有一工业机器人参数如下图所示:
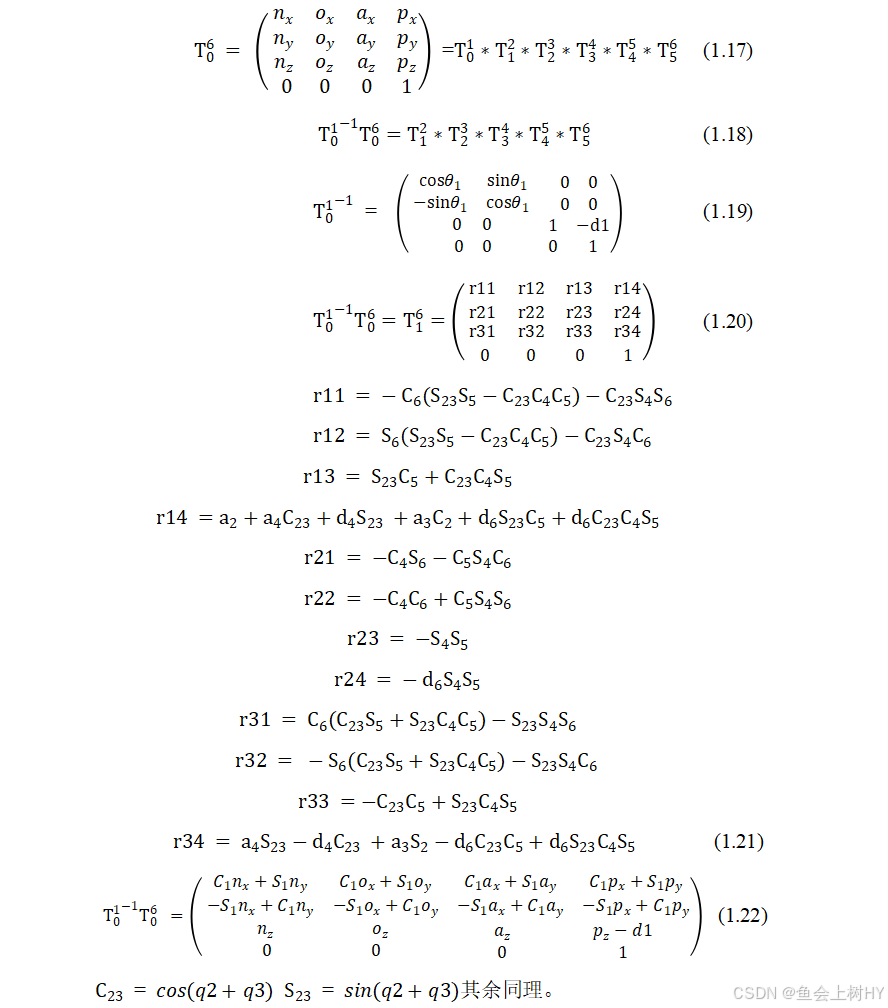




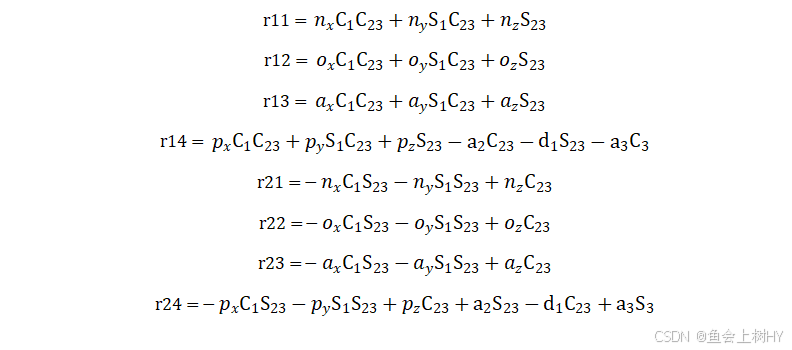



matlab代码
Matlab
clc;clear;
%带入机器人初始值
d1 = 0.670;
d4 = 1.280;
d6 = 0.215;
a2 = 0.312;
a3 = 1.075;
a4 = 0.225;
Position=[288.1, -433.1, 2832,96.9158, -29.6162, 109.3547];
px = Position(1)/1000;
py = Position(2)/1000;
pz = Position(3)/1000;
rx = Position(4);
ry = Position(5);
rz = Position(6);
posture = [rx,ry,rz]/180*pi;
a = Euler2RotMat(posture);
px = px - a(1,3)*d6;
py = py - a(2,3)*d6;
pz = pz - a(3,3)*d6;
%目标位置姿态矩阵
nx=a(1,1);ox=a(1,2);ax=a(1,3);
ny=a(2,1);oy=a(2,2);ay=a(2,3);
nz=a(3,1);oz=a(3,2);az=a(3,3);
% 求解关节角1
theta1_1 = - atan2(py,-px) ;
theta1_2 = - atan2(py,-px)+ pi ;
% 求解关节角3
c1_1 = cos(theta1_1);
s1_1 = sin(theta1_1);
c1_2 = cos(theta1_2);
s1_2 = sin(theta1_2);
Q = d4*d4+a4*a4;
M1 = ((c1_1*px+s1_1*py-a2)^2+(pz-d1)^2-a4*a4-d4*d4-a3*a3)/(2*a3);
M2 = ((c1_2*px+s1_2*py-a2)^2+(pz-d1)^2-a4*a4-d4*d4-a3*a3)/(2*a3);
theta3_1 = atan2(M1,sqrt(Q-M1^2))-atan2(a4,d4);
theta3_2 = atan2(M1,-sqrt(Q-M1^2))-atan2(a4,d4);
theta3_3 = atan2(M2,sqrt(Q-M2^2))-atan2(a4,d4);
theta3_4 = atan2(M2,-sqrt(Q-M2^2))-atan2(a4,d4);
% 求解关节角2
t1_1 = px*c1_1+py*s1_1-a2;
t1_2 = px*c1_2+py*s1_2-a2;
t2 = pz-d1;
A1 = a4+a3*cos(theta3_1);
A2 = a4+a3*cos(theta3_2);
A3 = a4+a3*cos(theta3_3);
A4 = a4+a3*cos(theta3_4);
B1 = -d4-a3*sin(theta3_1);
B2 = -d4-a3*sin(theta3_2);
B3 = -d4-a3*sin(theta3_3);
B4 = -d4-a3*sin(theta3_4);
theta2_1 = atan2(-B1,A1) + atan2(t2,t1_1) - theta3_1 ;
theta2_2 = atan2(-B2,A2) + atan2(t2,t1_1) - theta3_2 ;
theta2_3 = atan2(-B3,A3) + atan2(t2,t1_2) - theta3_3 ;
theta2_4 = atan2(-B4,A4) + atan2(t2,t1_2) - theta3_4 ;
% 求解关节角5
k1_1 = -nx*cos(theta1_1)*sin(theta3_1+theta2_1)-ny*sin(theta1_1)*sin(theta3_1+theta2_1)+nz*cos(theta3_1+theta2_1);
k1_2 = -nx*cos(theta1_1)*sin(theta3_2+theta2_2)-ny*sin(theta1_1)*sin(theta3_2+theta2_2)+nz*cos(theta3_2+theta2_2);
k1_3 = -nx*cos(theta1_2)*sin(theta3_3+theta2_3)-ny*sin(theta1_2)*sin(theta3_3+theta2_3)+nz*cos(theta3_3+theta2_3);
k1_4 = -nx*cos(theta1_2)*sin(theta3_4+theta2_4)-ny*sin(theta1_2)*sin(theta3_4+theta2_4)+nz*cos(theta3_4+theta2_4);
k2_1 = -ox*cos(theta1_1)*sin(theta3_1+theta2_1)-oy*sin(theta1_1)*sin(theta3_1+theta2_1)+oz*cos(theta3_1+theta2_1);
k2_2 = -ox*cos(theta1_1)*sin(theta3_2+theta2_2)-oy*sin(theta1_1)*sin(theta3_2+theta2_2)+oz*cos(theta3_2+theta2_2);
k2_3 = -ox*cos(theta1_2)*sin(theta3_3+theta2_3)-oy*sin(theta1_2)*sin(theta3_3+theta2_3)+oz*cos(theta3_3+theta2_3);
k2_4 = -ox*cos(theta1_2)*sin(theta3_4+theta2_4)-oy*sin(theta1_2)*sin(theta3_4+theta2_4)+oz*cos(theta3_4+theta2_4);
k3_1 = -ax*cos(theta1_1)*sin(theta3_1+theta2_1)-ay*sin(theta1_1)*sin(theta3_1+theta2_1)+az*cos(theta3_1+theta2_1);
k3_2 = -ax*cos(theta1_1)*sin(theta3_2+theta2_2)-ay*sin(theta1_1)*sin(theta3_2+theta2_2)+az*cos(theta3_2+theta2_2);
k3_3 = -ax*cos(theta1_2)*sin(theta3_3+theta2_3)-ay*sin(theta1_2)*sin(theta3_3+theta2_3)+az*cos(theta3_3+theta2_3);
k3_4 = -ax*cos(theta1_2)*sin(theta3_4+theta2_4)-ay*sin(theta1_2)*sin(theta3_4+theta2_4)+az*cos(theta3_4+theta2_4);
theta5_1 = atan2(sqrt(k1_1^2+k2_1^2),-k3_1);
theta5_2 = atan2(sqrt(k1_2^2+k2_2^2),-k3_2);
theta5_3 = atan2(sqrt(k1_3^2+k2_3^2),-k3_3);
theta5_4 = atan2(sqrt(k1_4^2+k2_4^2),-k3_4);
theta5_5 = -atan2(sqrt(k1_1^2+k2_1^2),-k3_1);
theta5_6 = -atan2(sqrt(k1_2^2+k2_2^2),-k3_2);
theta5_7 = -atan2(sqrt(k1_3^2+k2_3^2),-k3_3);
theta5_8 = -atan2(sqrt(k1_4^2+k2_4^2),-k3_4);
% 求解关节角6
theta6_1 = atan2(-k2_1/sin(theta5_1),k1_1/sin(theta5_1));
theta6_2 = atan2(-k2_1/sin(theta5_5),k1_1/sin(theta5_5));
theta6_3 = atan2(-k2_2/sin(theta5_2),k1_2/sin(theta5_2));
theta6_4 = atan2(-k2_2/sin(theta5_6),k1_2/sin(theta5_6));
theta6_5 = atan2(-k2_3/sin(theta5_3),k1_3/sin(theta5_3));
theta6_6 = atan2(-k2_3/sin(theta5_7),k1_3/sin(theta5_7));
theta6_7 = atan2(-k2_4/sin(theta5_4),k1_4/sin(theta5_4));
theta6_8 = atan2(-k2_4/sin(theta5_8),k1_4/sin(theta5_8));
% 求解关节角4
N1_1 = ax*cos(theta1_1)*cos(theta3_1+theta2_1)+ay*sin(theta1_1)*cos(theta3_1+theta2_1)+az*sin(theta3_1+theta2_1);
N1_2 = ax*cos(theta1_1)*cos(theta3_2+theta2_2)+ay*sin(theta1_1)*cos(theta3_2+theta2_2)+az*sin(theta3_2+theta2_2);
N1_3 = ax*cos(theta1_2)*cos(theta3_3+theta2_3)+ay*sin(theta1_2)*cos(theta3_3+theta2_3)+az*sin(theta3_3+theta2_3);
N1_4 = ax*cos(theta1_2)*cos(theta3_4+theta2_4)+ay*sin(theta1_2)*cos(theta3_4+theta2_4)+az*sin(theta3_4+theta2_4);
N2_1 = ax*sin(theta1_1)-ay*cos(theta1_1);
N2_2 = ax*sin(theta1_2)-ay*cos(theta1_2);
theta4_1 = atan2(N2_1/sin(theta5_1),N1_1/sin(theta5_1));
theta4_2 = atan2(N2_1/sin(theta5_5),N1_1/sin(theta5_5));
theta4_3 = atan2(N2_1/sin(theta5_2),N1_2/sin(theta5_2));
theta4_4 = atan2(N2_1/sin(theta5_6),N1_2/sin(theta5_6));
theta4_5 = atan2(N2_2/sin(theta5_3),N1_3/sin(theta5_3));
theta4_6 = atan2(N2_2/sin(theta5_7),N1_3/sin(theta5_7));
theta4_7 = atan2(N2_2/sin(theta5_4),N1_4/sin(theta5_4));
theta4_8 = atan2(N2_2/sin(theta5_8),N1_4/sin(theta5_8));
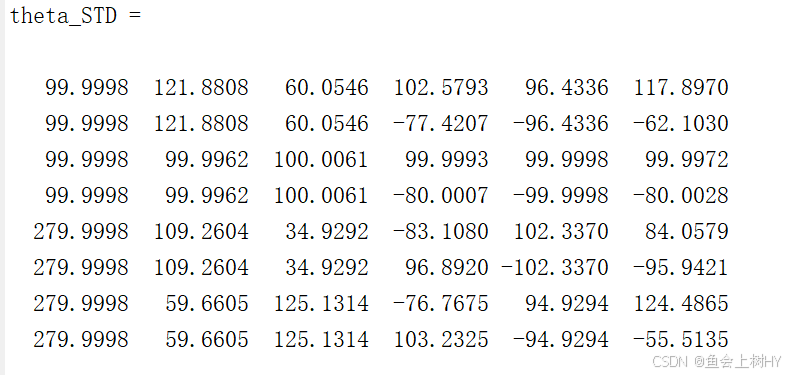
theta_STD = [
theta1_1,theta2_1,theta3_1,theta4_1,theta5_1,theta6_1;
theta1_1,theta2_1,theta3_1,theta4_2,theta5_5,theta6_2;
theta1_1,theta2_2,theta3_2,theta4_3,theta5_2,theta6_3;
theta1_1,theta2_2,theta3_2,theta4_4,theta5_6,theta6_4;
theta1_2,theta2_3,theta3_3,theta4_5,theta5_3,theta6_5;
theta1_2,theta2_3,theta3_3,theta4_6,theta5_7,theta6_6;
theta1_2,theta2_4,theta3_4,theta4_7,theta5_4,theta6_7;
theta1_2,theta2_4,theta3_4,theta4_8,theta5_8,theta6_8;
]*180/pi
function rotMat=Euler2RotMat(rpy)
rx=rpy(1);
ry=rpy(2);
rz=rpy(3);
cRx=cos(rx);
sRx=sin(rx);
cRy=cos(ry);
sRy=sin(ry);
cRz=cos(rz);
sRz=sin(rz);
rotMat=[cRz*cRy cRz*sRy*sRx-sRz*cRx cRz*sRy*cRx+sRz*sRx
sRz*cRy sRz*sRy*sRx+cRz*cRx sRz*sRy*cRx-cRz*sRx
-sRy cRy*sRx cRy*cRx];
end当输入:Position=[288.1, -433.1, 2832,96.9158, -29.6162, 109.3547]时(姿态用ZYX欧拉角表示,此数据来自机器人示教器上每个关节为100°时的正解值),结果为: