目录
[二、例题 P3225------宝藏排序Ⅰ](#二、例题 P3225——宝藏排序Ⅰ)
[四、例题 P3226------宝藏排序Ⅱ](#四、例题 P3226——宝藏排序Ⅱ)
一、排序
(一)冒泡排序
- 基本思想:比较相邻的元素,如果顺序错误就把它们交换过来。
(二)选择排序
- 基本思想:在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾
(三)插入排序
- 基本思想:将未排序数据插入到已排序序列的合适位置。
(四)快速排序
- 基本思想:选择一个基准值,将数组分为两部分,小于基准值的放在左边,大于基准值的放在右边,然后对左右两部分分别进行排序。
(五)归并排序
- 基本思想:将数组分成两个子数组,对两个子数组分别进行排序,然后将排序好的子数组合并成一个有序的数组。
(七)桶排序
- 基本思想:将待排序的数据元素,按照一定的规则划分到不同的"桶"中。每个桶内的数据元素再根据具体情况进行单独排序(通常可以使用其他简单排序算法,如插入排序),最后将各个桶中排好序的数据元素依次取出,就得到了一个有序的序列。
应用要点
时间复杂度:不同排序算法时间复杂度不同,如冒泡排序、选择排序、插入排序平均时间复杂度为 O(n^2),快速排序平均时间复杂度为 O(nlogn),归并排序时间复杂度稳定在 O(nlogn)。蓝桥杯题目对时间限制严格,大数据量下应优先选择 O(nlogn) 级别的排序算法。
空间复杂度:有些题目对空间也有限制。例如归并排序空间复杂度为 O(n),而快速排序如果实现合理(如原地分区)空间复杂度可以为 O(logn)。
稳定性:排序稳定性指相等元素在排序前后相对位置是否改变。例如插入排序、冒泡排序是稳定的,选择排序、快速排序是不稳定的。如果题目要求保持相等元素相对顺序,要选择稳定排序算法。
二、例题 P3225------宝藏排序Ⅰ
在一个神秘的岛屿上,有一支探险队发现了一批宝藏,这批宝藏是以整数数组的形式存在的。每个宝藏上都标有一个数字,代表了其珍贵程度。然而,由于某种神奇的力量,这批宝藏的顺序被打乱了,探险队需要将宝藏按照珍贵程度进行排序,以便更好地研究和保护它们。作为探险队的一员,肖恩需要设计合适的排序算法来将宝藏按照珍贵程度进行从小到大排序。请你帮帮肖恩。
输入描述
输入第一行包括一个数字 n ,表示宝藏总共有 n 个。
输入的第二行包括 n 个数字,第 ii 个数字 a[i] 表示第 i 个宝藏的珍贵程度。
数据保证 1≤n≤1000,1≤a[i]≤10^6 。
输出描述
输出 n 个数字,为对宝藏按照珍贵程度从小到大排序后的数组。
python# 冒泡排序 def bubble_sort(arr): n = len(arr) for i in range(n): for j in range(0, n - i - 1): if arr[j] > arr[j + 1]: arr[j], arr[j + 1] = arr[j + 1], arr[j] return arr # 选择排序 def selection_sort(arr): n = len(arr) for i in range(n): min_index = i for j in range(i + 1, n): if arr[j] < arr[min_index]: min_index = j arr[i], arr[min_index] = arr[min_index], arr[i] return arr # 插入排序 def insertion_sort(arr): n = len(arr) for i in range(1, n): key = arr[i] j = i - 1 while j >= 0 and key < arr[j]: arr[j + 1] = arr[j] j = j - 1 arr[j + 1] = key return arr # 快速排序 def quick_sort(arr): if len(arr) <= 1: return arr pivot = arr[len(arr) // 2] left = [x for x in arr if x < pivot] middle = [x for x in arr if x == pivot] right = [x for x in arr if x > pivot] return quick_sort(left) + middle + quick_sort(right) # 归并排序 def merge_sort(arr): if len(arr) <= 1: return arr mid = len(arr) // 2 left_half = arr[:mid] right_half = arr[mid:] left_half = merge_sort(left_half) right_half = merge_sort(right_half) return merge(left_half, right_half) def merge(left, right): result = [] left_index = 0 right_index = 0 while left_index < len(left) and right_index < len(right): if left[left_index] < right[right_index]: result.append(left[left_index]) left_index += 1 else: result.append(right[right_index]) right_index += 1 result.extend(left[left_index:]) result.extend(right[right_index:]) return result # 桶排序 def bucket_sort(arr): max_val = max(arr) min_val = min(arr) bucket_size = 1000 bucket_count = (max_val - min_val) // bucket_size + 1 buckets = [[] for _ in range(bucket_count)] for num in arr: index = (num - min_val) // bucket_size buckets[index].append(num) for i in range(bucket_count): buckets[i].sort() sorted_arr = [] for bucket in buckets: sorted_arr.extend(bucket) return sorted_arr n = int(input()) treasures = list(map(int, input().split())) print("冒泡排序结果:") print(bubble_sort(treasures[:])) print("选择排序结果:") print(selection_sort(treasures[:])) print("插入排序结果:") print(insertion_sort(treasures[:])) print("快速排序结果:") print(quick_sort(treasures[:])) print("归并排序结果:") print(merge_sort(treasures[:])) print("桶排序结果:") print(bucket_sort(treasures[:]))
三、各种排序比较
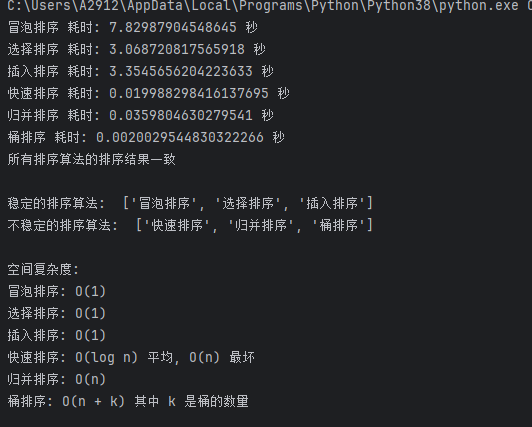
pythonimport time import random # 冒泡排序 def bubble_sort(arr): n = len(arr) for i in range(n): for j in range(0, n - i - 1): if arr[j] > arr[j + 1]: arr[j], arr[j + 1] = arr[j + 1], arr[j] return arr # 选择排序 def selection_sort(arr): n = len(arr) for i in range(n): min_index = i for j in range(i + 1, n): if arr[j] < arr[min_index]: min_index = j arr[i], arr[min_index] = arr[min_index], arr[i] return arr # 插入排序 def insertion_sort(arr): n = len(arr) for i in range(1, n): key = arr[i] j = i - 1 while j >= 0 and key < arr[j]: arr[j + 1] = arr[j] j = j - 1 arr[j + 1] = key return arr # 快速排序 def quick_sort(arr): if len(arr) <= 1: return arr pivot = arr[len(arr) // 2] left = [x for x in arr if x < pivot] middle = [x for x in arr if x == pivot] right = [x for x in arr if x > pivot] return quick_sort(left) + middle + quick_sort(right) # 归并排序 def merge_sort(arr): if len(arr) <= 1: return arr mid = len(arr) // 2 left_half = arr[:mid] right_half = arr[mid:] left_half = merge_sort(left_half) right_half = merge_sort(right_half) return merge(left_half, right_half) def merge(left, right): result = [] left_index = 0 right_index = 0 while left_index < len(left) and right_index < len(right): if left[left_index] < right[right_index]: result.append(left[left_index]) left_index += 1 else: result.append(right[right_index]) right_index += 1 result.extend(left[left_index:]) result.extend(right[right_index:]) return result # 桶排序 def bucket_sort(arr): max_val = max(arr) min_val = min(arr) bucket_size = 1000 bucket_count = (max_val - min_val) // bucket_size + 1 buckets = [[] for _ in range(bucket_count)] for num in arr: index = (num - min_val) // bucket_size buckets[index].append(num) for i in range(bucket_count): buckets[i].sort() sorted_arr = [] for bucket in buckets: sorted_arr.extend(bucket) return sorted_arr # ------------------------------------------------------------------------------------------------------------------------------------------ # 生成测试数据 test_array = [random.randint(1, 10000) for _ in range(10000)] # 记录每种排序的时间 sorting_methods = [ ("冒泡排序", bubble_sort), ("选择排序", selection_sort), ("插入排序", insertion_sort), ("快速排序", quick_sort), ("归并排序", merge_sort), ("桶排序", bucket_sort) ] # 比较排序结果 sorted_results = {} for name, sort_func in sorting_methods: start_time = time.time() sorted_array = sort_func(test_array[:]) end_time = time.time() sorted_results[name] = sorted_array print(f"{name} 耗时: {end_time - start_time} 秒") # 比较排序结果是否一致 base_result = sorted_results[sorting_methods[0][0]] is_consistent = True for name, result in sorted_results.items(): if result != base_result: is_consistent = False print(f"{name} 的排序结果与基准排序结果不一致") if is_consistent: print("所有排序算法的排序结果一致") # 比较稳定性 # 稳定性定义: 排序后相同元素的相对顺序不变 # 生成包含重复元素的测试数据 test_stability_array = [5, 3, 8, 3, 6] stable_sorts = [] unstable_sorts = [] for name, sort_func in sorting_methods: original_array = test_stability_array[:] sorted_array = sort_func(original_array) original_indices = [i for i, x in enumerate(original_array) if x == 3] sorted_indices = [i for i, x in enumerate(sorted_array) if x == 3] if original_indices == sorted_indices: stable_sorts.append(name) else: unstable_sorts.append(name) print("\n稳定的排序算法: ", stable_sorts) print("不稳定的排序算法: ", unstable_sorts) space_complexity = { "冒泡排序": "O(1)", "选择排序": "O(1)", "插入排序": "O(1)", "快速排序": "O(log n) 平均, O(n) 最坏", "归并排序": "O(n)", "桶排序": "O(n + k) 其中 k 是桶的数量" } print("\n空间复杂度:") for name, complexity in space_complexity.items(): print(f"{name}: {complexity}")四、例题 P3226------宝藏排序Ⅱ
问题描述
注意:这道题于宝藏排序Ⅰ的区别仅是数据范围在一个神秘的岛屿上,有一支探险队发现了一批宝藏,这批宝藏是以整数数组的形式存在的。每个宝藏上都标有一个数字,代表了其珍贵程度。然而,由于某种神奇的力量,这批宝藏的顺序被打乱了,探险队需要将宝藏按照珍贵程度进行排序,以便更好地研究和保护它们。作为探险队的一员,肖恩需要设计合适的排序算法来将宝藏按照珍贵程度进行从小到大排序。请你帮帮肖恩。
输入描述
输入第一行包括一个数字 n ,表示宝藏总共有 n 个。
输入的第二行包括 n 个数字,第 i 个数字 a[i] 表示第 i 个宝藏的珍贵程度。
数据保证 1≤n≤10^5,1≤a[i]≤10^9。
输出描述
输出 n 个数字,为对宝藏按照珍贵程度从小到大排序后的数组。
list.sort():是Python标准库中已经实现好的方法,它是基于优化的C语言代码实现的,内部实现经过了高度优化,以确保在各种情况下都能高效运行。
pythonn = int(input()) treasures = list(map(int, input().split())) # 使用Python内置的排序函数进行排序 sorted_treasures = sorted(treasures) for treasure in sorted_treasures: print(treasure, end=" ")